王金华, 向红军

(湘南学院数学与信息科学学院, 湖南 郴州 423000)

1.引言

分数阶微积分、分数阶差分与和分理论近二十年来有了较快的发展.相关理论在很多的领域, 比如: 生物工程、化学材料、控制理论等都有较为广泛的应用, 参见文[1-9]及所引参考文献.因此, 分数阶微分、差分方程理论与应用研究也受到了相关学者们广泛的关注, 涌现出不少关于分数阶微分、分数阶差分方程解的存在性及周期性等研究文献.由于分数阶微分方程研究出现比较早, 其方法也已经被不少研究者推广到了微分方程组的研究应用上.相对而言, 分数阶差分方程的研究相对较晚, 其理论与方法推广到分数阶差分方程组的研究也比较复杂.所以, 虽然出现不少分数阶差分方程的研究文献, 但分数阶差分方程组边值问题正解的研究文献不多, 文献中提出的边值条件也很少含分数阶差分算子.一般来说, 如果边界条件中带分数阶差分算子, 那么其格林函数相对复杂, 格林函数的性质应用相对困难.目前的文献中, 多数的边值条件是函数本身的两端函数值或是带函数的整数阶差分算子.如: 文[10]中, 作者分析了下列分数阶差分方程组边值问题解的存在性问题：

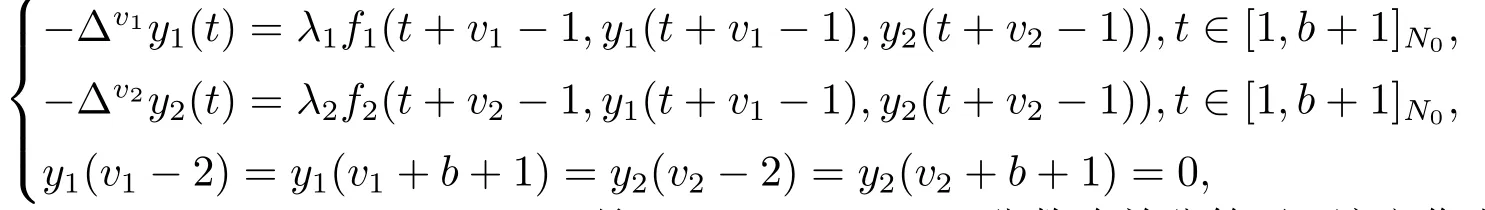
其中, 1＜v1,v2≤2,b ∈N1,Δv1,Δv2是Riemann-Liouville分数阶差分算子.该文作者应用不动点原理, 分析了以上分数阶边值问题至少有一个解的充分条件, 其方程组中的边界条件是函数在区间两端点函数值为0.

文[11]分析了下列分数阶差分方程组：

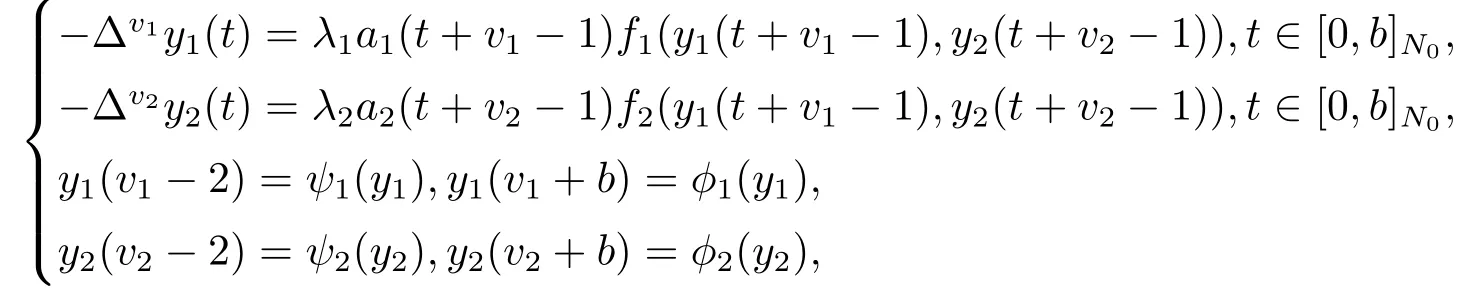
其中, 1＜v1,v2≤2,b ∈N1,Δv1,Δv2是Riemann-Liouville分数阶差分算子.作者用著名的Krasnosel’ski定理得到了此分数阶边值问题在满足一定条件时存在正解.其方程组中边界条件也是已知函数在区间两端点值.

文[12]的作者讨论了如下分数阶差分方程组的解存在性问题：

其中, 2＜vj ≤3,b ∈N1,b ＞3,λj ＞0,j=1,2,··· ,n,(j=1,2,··· ,n)是Caputo分数阶差分算子.在文[12]中作者应用相关不动点理论对该问题解的存在情况进行了讨论, 获得了一些充分条件, 也举例验证了理论的可靠性.其方程组中边界条件是函数在区间两端点函数值为0,边界条件中带有2阶差分算子.

文[10-12]中涉及的边值条件主要是函数本身的边界值或函数的整数阶差分边界值.本文将考虑如下具有分数阶差分边值条件的差分方程组问题：

其中,t ∈[0,b+1]N0, 对i= 1,2有1＜qi ≤2,0＜γi ＜1,0＜qi -γi ＜1,b ∈N1,b ＞3,Δqi,Δγi是Riemann-Liouville分数阶差分算子.ai:[qi-1,qi+b]→[0,+∞),gi:[0,+∞)×[0,+∞)→[0,+∞)均是连续函数.对任意a ∈R,I ⊂R,定义Na={a,a+1,a+2,···},INa=I ∩Na.对任意k ∈Na及Na上的函数u, 有

2.定义及引理

为了方便文章后面部分的讨论, 本节将介绍分数阶差分的定义及分数阶和分的定义.同时介绍在后面的证明中需要用到的一些结论.

定义2.1[3]对任意的t,v, 定义且规定当t+1-v是Γ函数的极点, 而t+1不是Γ函数的极点时, 有tv=0.

定义2.2[3]对于v ＞0, 函数f:Na →R的v阶和分定义如下：

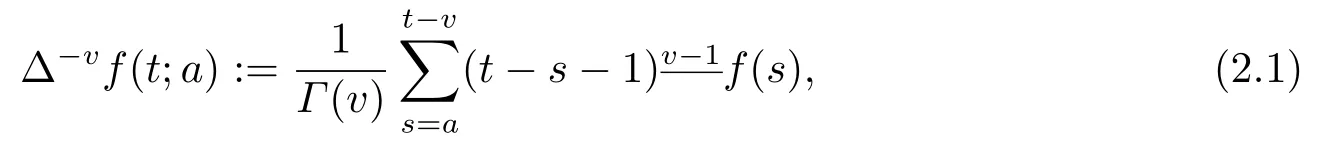
其中,t ∈{a+v,a+v+1,···}:=Na+v, 而函数f:Na →R的v阶Riemann-Liouville差分为：

Δvf(t):=ΔNΔ-(N-v)f(t),0≤N -1＜v ≤N,

ΔN是N阶向前差分算子.

引理2.1[3]设0≤N -1＜v ≤N, 则函数f:Na →R满足：

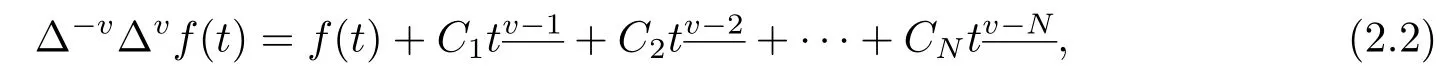
其中Ci ∈R,1≤i ≤N.

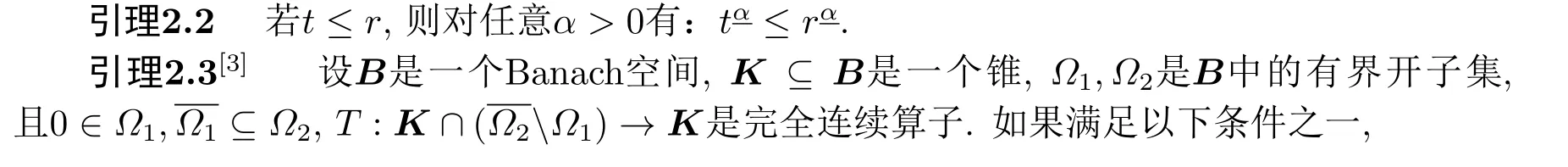
1) 当u ∈K ∩∂Ω1时,‖Tu‖≤‖u‖,且当u ∈K ∩∂Ω2时,‖Tu‖≥‖u‖;

2) 当u ∈K ∩∂Ω1时,‖Tu‖≥‖u‖,且当u ∈K ∩∂Ω2时,‖Tu‖≤‖u‖.

则T在K ∩(Ω2Ω1)中至少存在一个不动点.

引理2.4[9]设μ-1,μ+v+1非零或非负整数, 则有：

引理2.5[9]设1＜q ≤2, 函数g: [q-1,q+b]Nq-1→R, 则以下分数阶差分方程边值问题：

3.解的存在性

下面讨论判别分数阶方程组边值问题(1.1)存在正解的另一个充分条件, 后面的讨论中用到的条件记为：

定理3.2若条件(H1),(H2)和(H3)都成立, 则分数阶差分方程组边值题(1.1)至少有一个正解.

证由引理3.1可知T:K →K, 且由算子T的定义知能满足完全连续的性质.由条件(H3)可知, 存在正数ε使得：

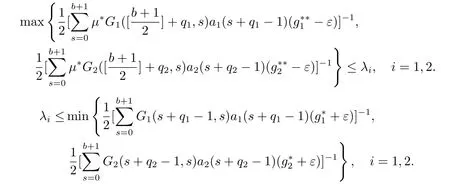
由条件(H1), 对以上的正数ε, 存在常数K1＞0, 使得当‖(u1,u2)‖＜K1时,

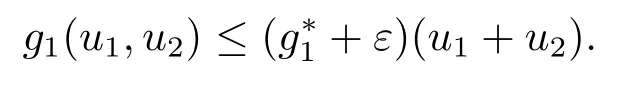
同理存在常数K2＞0, 使得当‖(u1,u2)‖＜K2时,

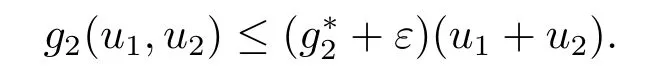
令K:= min{K1,K2}, 且记Ω1={(u1,u2)∈E:‖(u1,u2)‖ ＜K}, 则对任意(u1,u2)∈K ∩∂Ω1有:

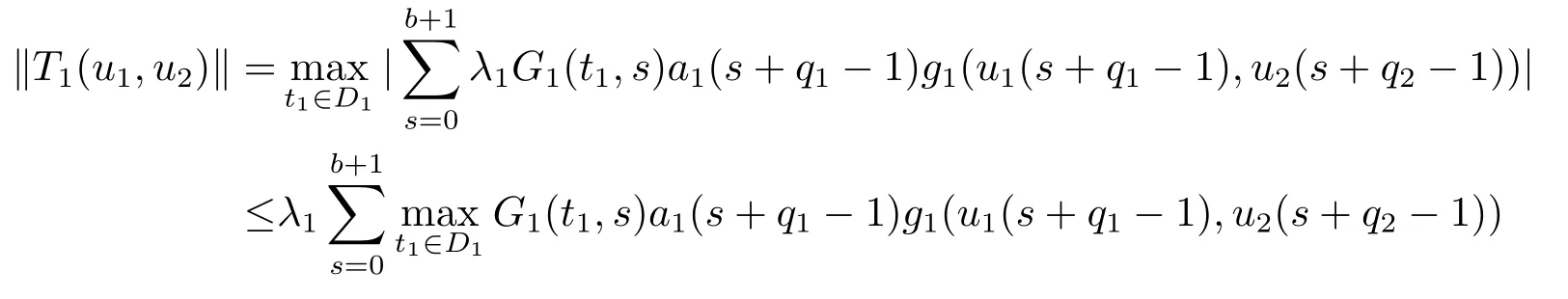
4.应用举例

例4.1考虑以下分数阶差分方程组边值问题：

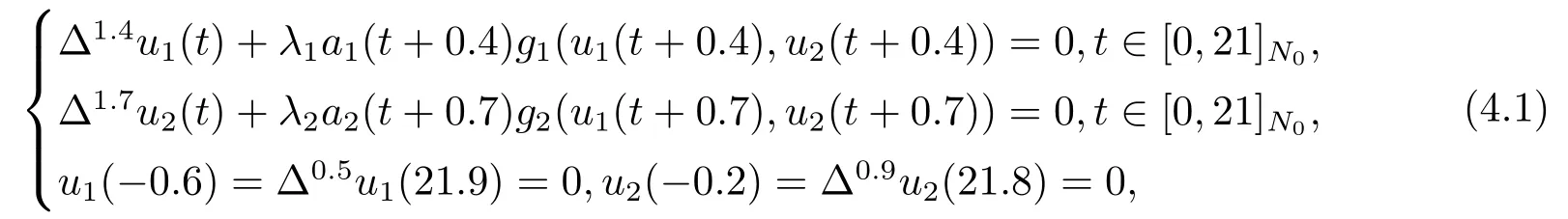
即q1=1.4,q2=1.7,γ1=0.5,γ2=0.9,b=20.取r1=1,r2=400,a1(t)=a2(t)=et-4,

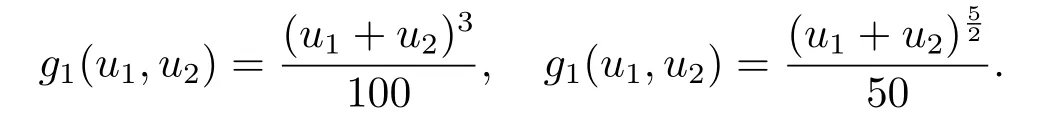
通过计算可得：α1=3.0350×108,α2=1.4292×109,β1=4.7768×105,β2=1.4970×106, 且

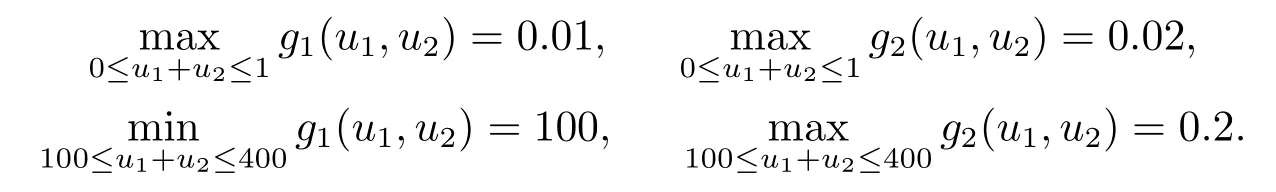
所以, 由定理3.2可知, 当λ1,λ2∈[4.5238×10-8,1.6474×10-5]时, 分数阶差分方程组(4.2)至少有一个正解.