刘 亮,龙 飞,杨 靖

(1.贵州大学电气工程学院，贵州 贵阳 550025；2.贵州理工学院人工智能与电气工程学院，贵州 贵阳 550003)

0 引言

符号稳定的概念来源于生态系统。生态领域的生物数量繁多且物种庞杂，受大自然等各种因素干扰却一直维持着生态平衡，呈现出巨大的稳定性与鲁棒性。研究人员把矩阵的符号与生态系统联系到一起，通过分析不同生态物种间的动态变化过程来研究符号稳定[1-2]，从而得出了符号稳定的概念，并且取得了一定的研究成果[3-4]。

不少研究者已经得出了符号稳定的必要条件，并将其与生态系统中的关系一一对应[5]。Jeffries等从矩阵主对角线元素符号出发，提出了一种涂色测试法[6]来判断矩阵的符号稳定，但该方法只对不可约矩阵有效。有相关学者从非对角线元素符号出发，分析一般矩阵符号稳定的充分条件[7]。由于符号稳定与矩阵元素大小无关，具有一种天然的鲁棒稳定性，所以许多研究人员把符号稳定运用到不确定动态系统中。例如，将符号稳定运用到凸多面体不确定系统中，利用符号稳定配置系统矩阵的元素符号，实现不确定系统的鲁棒镇定[8-10]。

上述研究成果充分体现了符号稳定的优越性。本文利用赫尔维茨稳定判据分析矩阵符号型，得到了相应符号稳定的充分条件。最后对符号稳定进行了拓展，以便更好地运用到一些混杂系统中。

1 符号稳定的概念

1.1 符号稳定的定义

实矩阵可以用一个有向图简单、直观地描述符号矩阵。

图1 实矩阵A的有向图

定义1[8]：如果与实矩阵A=(aij)n×n有相同符号型的任意实矩阵B都是赫尔维茨稳定的，则称实矩阵A是符号稳定的，实矩阵A的符号矩阵sgnA也是符号稳定的。

1.2 符号稳定的必要条件

定理1[8]：实矩阵A=(aij)n×n符号稳定的必要条件如下。

(1)∀i,aii≤0。

(2)至少存在一个i，使得aii<0。

(3)∀i≠j,aijaji≤0。

(4)对于阶数为三或三以上的实矩阵，都有aij·ajk· … ·aqr·ari=0。其中,i,j,k,…,q,r为元素的任意下标序列。

(5)detA≠0。

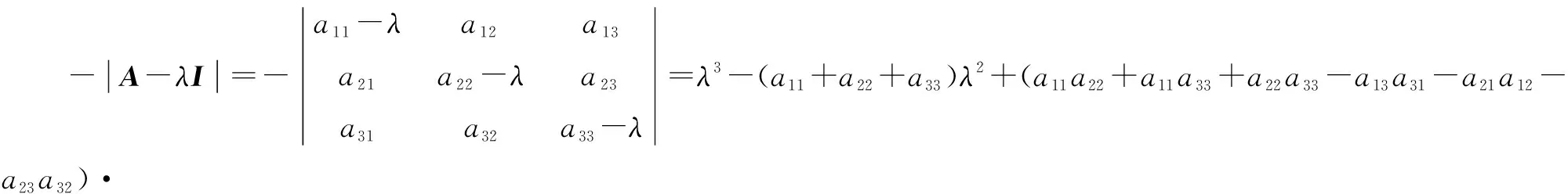
(1)

根据赫尔维茨稳定判据[11](线性系统稳定的必要条件是特征方程各项系数为正)，可知实矩阵A=(aij)n×n赫尔维茨稳定的必要条件为a11+a22+a33<0，(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)>0、(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)>0。

若实矩阵A=(aij)n×n为符号稳定矩阵，可知符号稳定必要条件⑤必然满足。

由a11+a22+a33<0可得aii≤0，且至少有1个为负，即符号稳定必要条件(1)和必要条件(2)。

由必要条件(1)和必要条件(2)可知a11a22+a11a33+a22a33≤0，而(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)>0，所以a13a31+a21a12+a23a32≤0，则aijaji≤0，即符号稳定必要条件(3)。

由必要条件(1)、必要条件(2)、必要条件(3)和必要条件(5)可知,(-a11a22a33+a13a31a22+a21a12a33+a23a32a11)>0，而(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)>0，所以a13a32a21+a12a23a31≤0，即a13a32a21≤0且a12a23a31≤0。当a12a23a31<0时，有以下2种情况。

①3个元素全为负:假设a12<0、a23<0、a31<0，由必要条件(3)可知这3个元素分别关于主对角线对称的元素a21≥0、a32≥0、a13≥0。当3个元素全部为正时，则a13a32a21>0，而a13a32a21+a12a23a31符号不确定，a13a32a21+a12a23a31≤0不一定成立。

②3个元素2正1负：假设a12>0、a23>0、a31<0，由必要条件(3)可知这3个元素分别关于主对角线对称的元素a21≤0、a32≤0、a13≥0，则a13a32a21≥0。当a13a32a21>0时，a13a32a21+a12a23a31的符号不确定，a13a32a21+a12a23a31≤0不一定成立。

综上所述，得a13a32a21=0，同理可证a12a23a31=0，即必要条件(4)。

1.3 符号稳定的充分条件

定理2：如果符号矩阵sgn[A=(aij)n×n]满足以下3个条件，那么sgn[A=(aij)n×n]是符号稳定的。

①∀i,aii<0。

②∀i≠j,aijaji=0。

③对于阶数为3以及3以上的实矩阵，都有aij·ajk· … ·aqr·ari=0。其中,i,j,k,…,q,r为元素的任意下标序列。

-|A-λI|=λ3-(a11+a22+a33)λ2+(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)λ+(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)=λ3-(a11+a22+a33)λ2+(a11a22+a11a33+a22a33)λ-a11a22a33=(λ-a11)(λ-a22)(λ-a33)

(2)

那么λi=aii<0(i=1,2,3)。

此结论可以扩展到任意阶矩阵。此符号稳定充分条件太过于严格，适用范围狭窄。下面将从必要条件出发，分析符号稳定充分条件的一般性结论。

2 符号稳定的定性分析

由定义1可知，对符号稳定进行定性分析，即分析符号矩阵的赫尔维茨稳定。因此，从赫尔维茨稳定判据入手，对符号稳定进行定性分析。

2.1 赫尔维茨稳定判据

以3阶实矩阵A=(aij)3×3为例，由式(1)和赫尔维茨稳定判据可知，实矩阵A赫尔维茨稳定的充要条件是a11+a22+a33<0、(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)>0、(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)>0，且需满足：

-(a11+a22+a33)(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)-(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)>0

(3)

定理3:当实矩阵A=(aij)3×3有符号矩阵sgn[A=(aij)3×3]时，实矩阵A=(aij)3×3符号稳定的充要条件如下。

①实矩阵A=(aij)3×3满足定理1。

②-(a11+a22+a33)(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)-(-a11a22a33-a13a32a21-a12a23a31+a13a31a22+a21a12a33+a23a32a11)>0成立。

由定理1的必要条件(4)可知，式(3)可以简写为：

(4)

结合定理1和式(4)可知，对符号稳定进行定性分析，即分析矩阵主对角线元素aii的符号与关于主对角线对称的元素aijaji的符号的关系，也就是对应定理1中的必要条件(2)和必要条件(3)。

2.2 不可约矩阵的符号稳定充分条件

针对主对角线的元素符号，Jeffries等给出了1种涂色测试法[5-6]，用来判断矩阵的符号稳定。但此法局限于不可约矩阵。

定义2：如果矩阵A是不可约矩阵(不可分解)，对于所有的i≠j，在矩阵A的有向图中，有且仅有一条路径从i到j。

定义3：矩阵A=(aij)n×n是1个可约矩阵，如果将1,2,…,n分成2个不相交的非空集合{i1,i2,…,iμ}和 {j1,j2,…,jv}，且μ+v=n，就使得aiαjβ=0，α=1,2,...,n,β=1,2,...,v。

定理4：如果符号矩阵的主对角线元素全为负数且满足符号稳定的必要条件，则此符号矩阵是符号稳定的。

对于三阶符号矩阵，由定理1的必要条件(3)和aii<0可知，式(4)必然成立。此3阶符号矩阵为符号稳定矩阵。对于n阶符号矩阵，可依据此方法进行证明。

定理5：对于不可约的符号矩阵，如果满足符号稳定的必要条件且涂色测试法失效，则此符号矩阵是符号稳定的。

涂色测试法主要针对符号矩阵主对角线元素。矩阵主对角线元素为负数时，定义为黑色节点，表示为aib,ib；矩阵主对角线元素为0时，定义为白色节点，表示为aiw,iw。当矩阵主对角线元素仅有黑色节点或仅有白色节点时，不必进行涂色测试。因为主对角线元素仅有黑色节点时，可用定理4进行判定; 仅有白色节点时，不满足符号稳定的必要条件，不是符号稳定的。因此，涂色测试主要针对黑色节点与白色节点共存的情况。在进行涂色测试之前，已确定矩阵满足符号稳定的必要条件。进行涂色测试法的具体操作步骤如下。

①如果1个符号矩阵涂色测试成功，则表示所有aiw,jwajw,iw形式的乘积中，至少有1个此形式的乘积结果为负数。如果仅有1个白色节点，无法构成形如aiw,jwajw,iw的乘积形式，则涂色测试失效。如果仅有2个白色节点，可以构成1个形如aiw,jwajw,iw的乘积形式且乘积结果为负数，则涂色测试成功。

②所有ajb,iwaiw,jb形式的乘积中，对于黑色节点jb，当ajb,iwaiw,jb的乘积结果为负数，且ajb,kwakw,jb的乘积结果也为负数(iw≠kw)时，则涂色测试成功。

以3阶矩阵为例，对于1个不可约的3阶符号矩阵sgn[A=(aij)3×3]，如果它是符号稳定的，则其满足定理1且式(4)成立，即式(5)～式(10)成立。

a11+a22+a33<0

(5)

(a11a22+a11a33+a22a33-a13a31-a21a12-a23a32)>0

(6)

-a11a22a33+a13a31a22+a21a12a33+a23a32a11>0

(7)

a13a32a21=0

(8)

a12a23a31=0

(9)

(10)

其中，式(5)～式(9)式是符号矩阵sgn[A=(aij)3×3]符号稳定的必要条件，式(5)～式(10)是矩阵sgn[A=(aij)3×3]符号稳定的充要条件。在使用涂色测试法之前，已知矩阵满足式(5)～式(9)，所以涂色测试法是从定理1中的必要条件(2)入手，针对式 (10)而设计的。

2.3 一般矩阵符号稳定的充分条件

涂色测试法虽然提供了完整的、判断符号稳定的充分条件，但方法复杂，使用繁琐，且局限性大。因此，研究者提出了1种比较简单的充分条件来验证符号稳定。与涂色测试法不同的是，此方法是从定理1的必要条件(3)入手，针对式(10)而设计的。

分析一般矩阵符号稳定充分条件的预备知识点[7]如下。

①关于主对角线对称的2个元素的乘积算式称为相互作用对，即aijaji(i≠j)。如果aijaji<0，则称aijaji为OS对。如果aijaji=0，则称aijaji为ZS对。在aijaji=0中，如果2个元素符号分别为正和零，则称aijaji为ZSp对。如果2个元素符号分别为负和零，则称aijaji为ZSn对。如果2个元素符号都为零，则称aijaji为ZZ对。

②满足定理1条件的矩阵定义为ISS矩阵；满足符号稳定充分条件的矩阵定义为QLSS矩阵。

③矩阵的主对角线上，关于中点对称的2个元素相加的形式定义为MIDMT,如4阶矩阵中的a11+a44和a22+a33。主对角线任意2个元素的相加定义为MT，如4阶矩阵中的a11+a22、a33+a44和a11+a33等。

n阶ISS矩阵最多有(n-1)个OS对，当超过(n-1)个OS对时，将不满足定理1中的必要条件(4)。由定义2可知，n阶不可约矩阵有且仅有(n-1)个OS对，其余全为ZZ对。

下面将从OS对的个数来分析符号稳定的充分条件。

定理6：1个n阶ISS矩阵的OS对个数为0，则为QLSS矩阵。

证明：以3阶矩阵为例，n阶矩阵可按照此方法证明。

3阶ISS矩阵sgn[A=(aij)3×3]必满足式(5)～式(9)。3阶QLSS矩阵sgn[A=(aij)3×3]必满足式(5)～式(10)。如果3阶ISS矩阵sgn[A=(aij)3×3]中OS对的个数是0，则由式(5)和式(7)可知a11<0、a22<0,a33<0，式(10)必然成立。

定理7：如果1个n阶ISS矩阵的OS对个数小于(n-1)个，且满足下列任意1个条件，则为QLSS矩阵。

①n阶ISS矩阵中所有QS对使得相应的MT非零。

②n阶ISS矩阵中所有ZSp对使得相应的MT非零。

定理8：如果1个n阶ISS矩阵的OS对个数是(n-1)，且满足下列任意1个条件，则为QLSS矩阵。

①反主对角线上至少存在1个OS对，使得相应的MIDMT非零。

②反主对角线上至少存在1个ZZ对，使得相应的MIDMT非零。

定理5和定理8描述的是同一种符号矩阵。不同的是，定理5中的涂色测试法是从主对角线元素的符号来分析符号稳定，定理8是从反主对角线相互作用对的符号来分析符号稳定。

定理9：一个可约的ISS矩阵A可以分解为q个Ai，即detA=detA1×detA2×…×detAq。当且仅当Ai(i=1,2,...,q)全为QLSS矩阵时，A是QLSS矩阵。

注1：对于1个n阶ISS矩阵，如果OS对的个数小于(n-1)个，且可分解为多个矩阵。根据定理9可知，分析n阶ISS矩阵的符号稳定性，等同于分析分解的多个矩阵的符号稳定性。

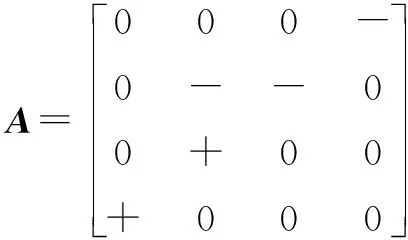
图2 A和B的有向图(I)

3 符号稳定的验证示例

验证：矩阵A是1个5阶ISS矩阵，有4个OS对，是1个不可约矩阵。可用定理5和定理8进行判断。运用定理5对其进行涂色测试，a11、a22、a44、a55是黑色节点，a33是白色节点。使用涂色测试法进行验证，涂色测试成功，所以A不是1个QLSS矩阵。运用定理8，不满足条件①和条件②，所以A不是一个QLSS矩阵。

验证：矩阵A是1个5阶ISS矩阵，有4个OS对，是1个不可约矩阵。可用定理5和定理8进行判断。运用定理5对其进行涂色测试，a22、a33、a44、a55是黑色节点，a11是白色节点。使用涂色测试法进行验证：涂色测试失效，所以A是1个QLSS矩阵。运用定理8，因为矩阵A满足条件②，所以A是1个QLSS矩阵。

验证：矩阵A是1个4阶ISS矩阵，有2个OS对。可用定理7进行判断：矩阵A不满足条件①，而条件②不适用于矩阵A，所以A不是1个QLSS矩阵。通过有向图可知，矩阵A可以分解为2个矩阵，用定理9进行判断。因为其中1个分解矩阵不是QLSS矩阵，所以A不是1个QLSS矩阵。

验证：矩阵A是1个4阶ISS矩阵，有2个OS对和2个ZSn对。可用定理7进行判断：矩阵A满足条件①，而条件②不适用于矩阵A，所以A是1个QLSS矩阵。

4 符号稳定的相关结论

定理10：如果1个矩阵的有向图结构与1个QLSS矩阵的有向图结构相同，则这个矩阵也是QLSS矩阵。

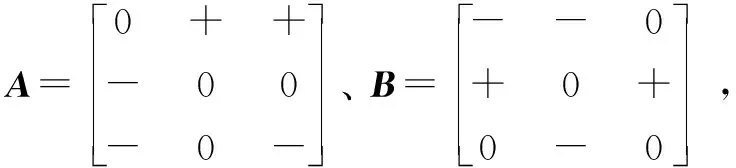
图3 A和B的有向图(II)

证明：假设A为QLSS矩阵;P为1个与A阶数相同的置换矩阵，B=PTAP,因此A与B合同。由合同的性质可知，A和B有相同的正负惯性指数，即正负特征值个数相同。因为A是QLSS矩阵，所以B也是QLSS矩阵。此时，A和B的有向图结构相同。

对A作初等变换，不会改变A的有向图结构。一次初等行变换和一次对应的初等列变换对应着有向图2个对应位置处的节点交换。

定义4：由具有相同有向图结构的符号矩阵组成的1个符号矩阵集合，如果其中任意1个符号矩阵是符号稳定的，则称这个集合为稳定集。如果矩阵的阶数是n，其子集个数为n!，则称这个集合为完整稳定集。

这个矩阵的有向图结构相同的矩阵构成的1个完整稳定集为：

定理11[8]：对于所有符号稳定且主对角线元素均为负数的n阶矩阵A=(aij)n×n，其所有特征值的实部有界且满足以下要求。特征值实部绝对值的下界是所有对角线元素绝对值的最小值，特征值实部绝对值的上界是所有对角线元素绝对值的最大值，即：

|aii|min≤|Re(λi)|min≤|Re(λi)|max≤|aii|max

(11)

对于A=(aij)n×n部分主对角线元素为0的情况，有：

0<|Re(λi)|min≤|Re(λi)|max≤|aii|max

(12)

给定1个n阶矩阵An×n和1个m阶矩阵Bm×m，⊗表示Kronecker积[12]，⊕表示Kronecker和[12]。

(13)

引理12[12]：矩阵An×n的特征值是λi(i=1,2,…,n)，矩阵Bm×m的特征值是μj(j=1,2,…,m)，则An×n⊕Bm×m的特征值为λi+μj(i=1,2,…n;j=1,2,…,m)。

定理13：如果sgn[A=(aij)n×n]和sgn[B=(aij)m×m]都是符号稳定的，则sgn[A=(aij)n×n]⊗sgn[B=(aij)m×m]也是符号稳定的。

证明：假设sgn[A=(aij)n×n]的特征值是λi，sgn[B=(aij)m×m]的特征值是μj。因为sgn[A=(aij)n×n]和sgn[B=(aij)m×m] 都是符号稳定的，所以Re(λi)<0、Re(μj)<0，可得Re(λi+μj)<0。由引理12可知，sgn[A=(aij)n×n]⊗sgn[B=(aij)m×m]也是符号稳定的。

赫尔维茨稳定和Schur稳定是2种非常重要的稳定概念。符号稳定是1种打破传统数值型的赫尔维茨稳定。下面将进一步分析符号矩阵与Schur稳定之间的联系。

如果矩阵A=(aij)n×n满足aijaji=0(i≠j)，且对于阶数为3或3以上的矩阵都有aij·ajk· … ·aqr·ari=0(i,j,k,…,q,r为元素的任意下标序列)，那么矩阵A=(aij)n×n的特征值为主对角线元素。

定理14：当符号矩阵sgn[A=(aij)n×n]满足以下条件时，矩阵A=(aij)n×n是Schur稳定的。

①|aii|<1。

②aijaji=0(i≠j)。

③对于阶数为3或3以上的矩阵都有aij·ajk· … ·aqr·ari=0。其中i,j,k,…,q,r为元素的任意下标序列。

定理15：当符号矩阵sgn[A=(aij)n×n]满足以下条件时，矩阵A=(aij)n×n是Schur稳定的。

①0≤aii<1。

②aijaji=0(i≠j)。

③对于阶数为3或3以上的矩阵都有aij·ajk·…·aqr·ari=0。其中，i,j,k,…,q,r为元素的任意下标序列。

定理14和定理15分别对一般矩阵和正矩阵定义了1种符号型Schur稳定。在一般矩阵中，其相互作用对可以是ZSp对、ZSn对或 ZZ对。在正矩阵中，其相互作用对只能是ZSp对或ZZ对。

定理16：当符号矩阵sgn[A=(aij)n×n]满足以下条件时，则矩阵A=(aij)n×n既是Schur稳定的，又是赫尔维茨稳定的。

①-1

②aijaji=0(i≠j)。

③对于阶数为3或3以上的矩阵都有aij·ajk·…·aqr·ari=0。其中,i,j,k,…,q,r为元素的任意下标序列。

定理17：如果符号矩阵sgn[A=(aij)n×n]是正矩阵，则以下2个条件等价。

①sgn[A=(aij)n×n]是Schur稳定的。

②sgn[A=(aij)n×n]-In×n是赫尔维茨稳定的。

证明：条件①→条件②。由定理15可知，如果sgn[A=(aij)n×n]是Schur稳定的，则0≤aii<1。对于矩阵sgn[A=(aij)n×n]-In×n，其对角线元素aii-1<0。由定理16可知，sgn[A=(aij)n×n]-In×n是赫尔维茨稳定的。

条件②→条件①。由定理16可知，如果sgn[A=(aij)n×n]-In×n是赫尔维茨稳定，则aii-1<0，得aii<1。由正矩阵sgn[A=(aij)n×n]得aii>0，所以0≤aii<1。由定理15可知,sgn[A=(aij)n×n]是Schur稳定的。

5 结论

本文通过定义符号稳定，首先从符号稳定的必要条件出发，利用赫尔维茨稳定判据分析了符号稳定的充分条件。然后，用具体例子来验证所得的充分条件，对符号稳定充分条件作出了一般性结论。最后，将符号稳定推广到符号Schur稳定，使其在一些不确定系统(例如随机系统、切换系统等)中的应用更加广泛。