Xiaoyan Zhang | Liangming Chen | Shuai Li | Predrag Stanimirović |Jiliang Zhang | Long Jin

1School of Information Science and Engineering,Lanzhou University,Lanzhou, China

2Faculty of Sciences and Mathematics,University of Niš, Niš,Serbia

3Department of Electronic and Electrical Engineering, The University of Sheffield,Sheffield,UK

Abstract A special recurrent neural network (RNN), that is the zeroing neural network (ZNN), is adopted to find solutions to time-varying quadratic programming(TVQP)problems with equality and inequality constraints. However, there are some weaknesses in activation functions of traditional ZNN models, including convex restriction and redundant formulation. With the aid of different activation functions, modified ZNN models are obtained to overcome the drawbacks for solving TVQP problems. Theoretical and experimental research indicate that the proposed models are better and more effective at solving such TVQP problems.

1 | INTRODUCTION

As a kind of common and basic optimisation problem[1],the quadratic programming(QP)problem is extensively available in various scientific and technological fields[2,3],such as pattern recognition[4],signal processing[5,6]and robotics[7–10].In order to deal with such problems,numerous target approaches are put forward,most of which require numerical calculations.However, the complexity and costs of numerically solving QP problems are rather high,which is proportional to the cube of the dimension of its associated Hessian matrix[11–13].Therefore, when dealing with relatively complex problems, most arithmetical methods are time-consuming and evenfail to get the results.For these reasons,more efficient and accurate methods are needed.

As advancements in artificial intelligence are racing ahead[14, 15], recurrent neural network (RNN), as a significant branch, is also evolving rapidly and increasing in popularity[16–19]. Owing to its highly suitable nature of easy hardware implementation, parallel computing and adaptive self-learning,this intelligent method can be used to deal with scientific and engineering problems with strong real-time requirements and large calculation scale [20, 21]. Typically, RNN models used for the solution of these QP problems are based on gradient methods [22, 23], instead of one with a time-variant coefficient. However, these traditional static approaches lack timederivative information and therefore they can only solve QP problems with time-invariant coefficients. Both theories and practice show that, if parameters in the given system change over time, there will be time-lag errors. For this reason,Zhang et al. presented and discussed a new kind of RNN method to solve time-varying quadratic programming(TVQP) problems utilising the matrix-valued error function,which is called the zeroing neural network (ZNN) [24]. The ZNN approach differs from the traditional gradient neural network (GNN) whose energy function is scalar valued [25].On account of the involvement of time-derivative information of the parameters, the large time-lag errors could be drastically reduced and the solution to the TVQP problem is well tracked [26]. It has been shown to be powerful when dealing with some time-variant problems including the online matrix inversion.

As research continues, scientists have made some vital new discoveries in the study of ZNN. For example, they have found that the activation function is a highly essential factor influencing the convergence performance of the ZNN model. Also, many variants of ZNN appear with different activation functions. In [27], an improved ZNN model aided with the sign-bi-power (SBP) function was presented and investigated, attracting a great deal of attention due to its finite-time convergent performance. For clarity and brevity,this finite-time convergent model is referred to here as the sign-bi-power ZNN model (SBPZNN) according to its activation function. Although many achievements have been made in the existing ZNN models in solving TVQP problems [28], there remains much scope for improvement due to some common limitations to be resolved. Two shortcomings in the existing ZNN models are specifically described and adequate solutions to overcome them are also provided herein. On one hand, the projection of the activation function of ZNN models must be convex, differentiable and monotonic, which is somewhat unnecessary and may even block the development progress of ZNN. On the other hand, the redundant expression of the SBP activation function leads to a slow converging rate [29], which similarly affects the performance of the SBPZNN model. To solve the first limitation, a ZNN model allowing non-convex projection on activation functions (i.e. NPZNN model) so as to remove the convex restriction is proposed. To solve the second limitation, a ZNN model aided with a simpler SBP function (i.e. SSZNN model), a combined function-activated ZNN model (i.e. CZNN model) and a ZNN model activated with saturation function (i.e. SZNN model) are adopted separately, thereby accelerating the convergence speed. In short, the newly proposed models have disparate propensities, all of which are of great significance to ZNN for solving TVQP problems. Finally, the concluding section provides a summary on the authors’ work and gives some suggestions for future research on ZNN models and their real-world applications.

In Section 2, the authors introduce the definition and transformation process of the TVQP problem, as well as the corresponding ZNN model and its design process. In Section 3, several modified ZNN models are proposed aimed at remedying the weaknesses of the traditional ZNN models stated earlier,and then their convergence is proven through the related theoretical analysis. In Section 4, several numerical simulations are conducted and the results are analyzed for further validating the effectiveness of the proposed ZNN models for solving TVQP problems.

2 | PROBLEM FORMULATION AND ZNN SOLVERS

A TVQP problem constrained by equalities and inequalities and its transformation process are elaborated on in detail early in this section.The SBPZNN model and its design process are also provided to establish the foundation for further research and improvement. In addition, limitations to existing ZNN models are presented.

2.1 | Problem formulation

The intended target is to construct some appropriate ZNN models for better solving TVQP problems, especially those with equality and inequality constraints. The standard form is described as follows:

In (1), V(t)∈Rn×nis a positive-definite and time-dependent Hessian matrix; vectors v(t)∈Rn, b1(t)∈Rm, b2(t)∈Rpare given vectors, full rank matrix A1(t)∈Rm×nand matrix A2(t)∈Rp×nare with time-variant entries;vector x(t)∈Rnis solved at any time t so that the objective function reaches its minimum; symbolTshows the transpose of the vector.

To solve TVQP problem(1),a Lagrangian function is first constructed,as shown in the following,so as to transform the TVQP problem into the problem of finding the extreme value of the Lagrangian function:

where vector ϱ(t)∈Rmrepresents the Lagrangian multiplier constrained by equality and vector ς(t)∈Rprepresents the one constrained by inequality. Then the following lemma is obtained to get the solution to the above problem:

Lemma 1 ( [5, 30]). If unique vectors x*(t), ϱ*(t) and ς*(t) simultaneously meet KKT conditions shown in the following, x*(t)∈Rnwill be the minimum of TVQP (1):

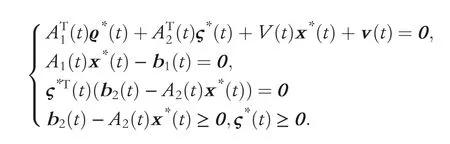
Through Lemma 1 we know that the TVQP problem(1) can be solved by converting it into a time-varying nonlinear equation. To achieve this transformation, the following theories are utilised. Firstly, the definition of the non-linear complementary problem (NCP) is given as follows.

Definition 1 ([30]). A function φ(a1,a2),Rn×Rn→Rncan be termed NCP if the following condition is satisfied:

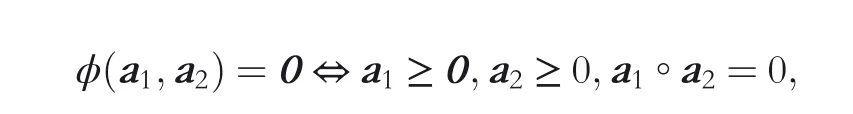
where ◦is the symbol of Hadamard product. A commonly used NCP function is the Fischer-Burmeister (FB) function,which is identified as

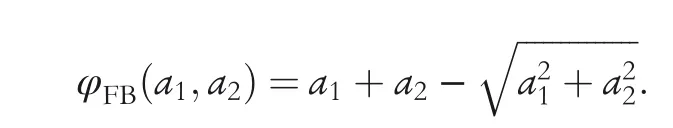
In this case, finding the solution to the NCP problem can be turned into solving the equations:

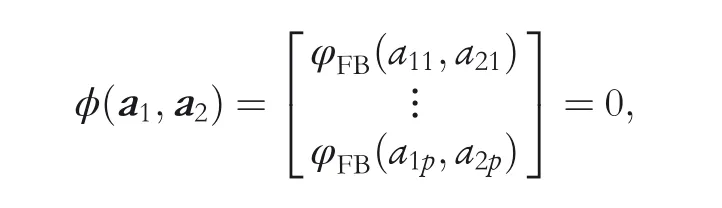
Since the function φ(·) is non-differentiable at the point(0,0)in the case of scalars,smooth parameters are introduced to obtain the following smooth continuous and differentiable PFB function:

if and only if x*(t) is the KKT point.

According to theorems in[32],conversion from the above equations to an equivalent time-varying equation is necessary,which means that the optimal solution to (1) will be worked out only if the result of the following non-linear matrix equation is satisfied:

2.2 | ZNN solvers

In general,when solving time-varying problems with the ZNN method, an error function associated with the problem to be solved is firstly defined.By substituting it into the ZNN design formula,a ZNN model with a given activation function is thus designed.The error function is regulated to zero and then the solution is obtained.

To track the solving process, firstly define the following error function which is vector-valued indefinite:

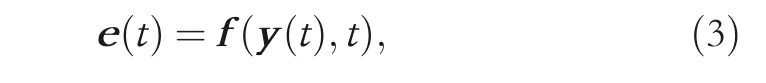
where each element can be positive, zero or negative. The design formula of ZNN is then adopted as follows:

where the design parameter γ ＞0 ∈R is a crucial factor in determining the converging speed of the neural network.Moreover, given certain hardware conditions, the value of γ should be appropriately selected according to the simulation and experimental requirement or as large as possible; ψ(·)represents an array of activation function which is also essential in constructing ZNN and is typically monotonically increasing odd. Through a combination of the error in (3) and the design formula (4), the ZNN model designed for finding solutions to Equation (2) is naturally derived, and is depicted by the implicit dynamic equation in the following:

and D1(t)=∧(d(t) ⊘z(t)) and D2(t)=∧(ς(t)⊘z(t)),where ∧(·) and ⊘separately denote diagonal matrices as well as the Hadamard division [32]. For convenience of calculation and implementation, the ZNN model (5) is thus equivalently converted into the formulation displayed as

To realize finite-time convergence, the SBP function is commonly employed in the construction of ZNN models,and the formulation is shown as

where eiis the i-th element of error e(t) and τ represents a design parameter in range (0, 1). The definition of Lfτ(·) is given as follows:

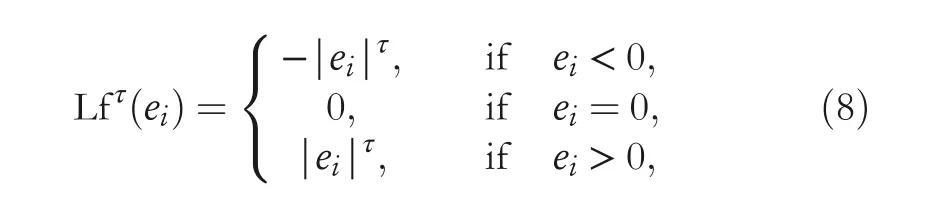
where |·| is a symbol presenting the absolute value of an element. The introduction to the SBPZNN model (6) is thus completed.

When solving TVQP problems, two common limitations appear in the existing ZNN models.The first limitation is that non-convex projection sets cannot exist in the activation function, and the second limitation is about SBPZNN, whose convergence rate is not satisfactory due to its redundant formulation.ZNN models with non-convex set and fast finitetime convergence speed remain to be explored.

3 | MODIFIED ZNN SOLVERS

In consideration of the limitations of the traditional ZNN models described in the previous section,four modified ZNN models based on different kinds of activation functions are developed and analysed in this section.

3.1 | Non‐convex projection activated ZNN

Firstly, a projection is defined, that is, PΩ(ζ)=argminω∈Ω‖ω-ζ‖2with 0 ∈Ω where Ω is a set of n-dimensional vectors. Thus the design formula (4) is rewritten as:

Through a combination of Equations(6)and(9),a new NPZNN model with non-convex projection is conveniently derived as

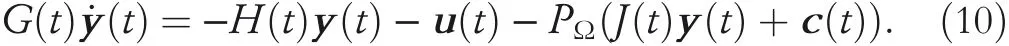
Note that the NPZNN model(10)is extended by its design formula.Therefore,it later can be directly applied to prove the theorem presented in the following part.

Theorem 1 NPZNN model (10) globally converges to the time‐varying theoretical solution y*(t) of Equa‐tion(2)whose first n members are the optimal solution to the TVQP problem (1).

Proof. Firstly, define a Lyapunov function candidate as

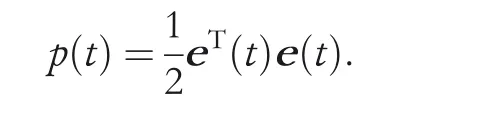
Clearly we know that if e(t)≠0, p(t) ＞0 is obtained and that p(t)=0 only when situation e(t)=0 is satisfied,indicating the positive definiteness of p(t). Then, taking the time derivative of given function p(t) leads to

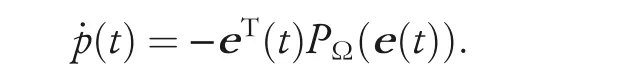
Based on the definition of PΩ(e(t)), that is mapping from the set of e(t) to set Ω, the following inequation can be obviously derived:

Based on the Lyapunov stability theorem,it can be deduced that(3)converges to zero globally,from which the conclusion that NPZNN model (10) converges globally to the theoretical solution to Equation (2) can be further drawn. The proof of global convergence of model(10)is thus complete.

Theorem 1 demonstrates that activation functions in the existing ZNN models, such as linear function and SBP function, are subcases of PΩ(·). In addition to these common activation functions, the following special sets are also able to serve as activation functions for NPZNN models to deal with the exceptional conditions.

3.2 | ZNN model with simplified SBP activation function

Considering that the formulation of SBP function is too redundant for SBPZNN model(6)to converge at a fast rate,a simplified SBP function is thus adopted:

Then, the following theorems on SSZNN model (12) are presented for the study of the convergence.

Theorem 2 SSZNN model (12) globally converges to the theoretical solution y*(t) of Equation (2) whose first n members are the optimal solution to the TVQP problem (1).

Proof.As a subcase of NPZNN model(10),SSZNN model(12)also applies to Theorem 1.Thus extra proof can be omitted here.Theorem 3 SSZNN model (12) converges to the theo‐retical solution y*(t) of Equation (2) in finite time tcand the first n members of y*(t) are the optimal so‐lution to TVQP problem (1) with tc= ｜emax(0)｜1-τ/(γ(1 - τ)), where emax(0) is the one possessing the maximum absolute value among all elements of the initial vector e(0) = J(0)y(0) + c(0).

Proof. Rewriting SSZNN model (12) generates ˙e(t)=-γS(e(t)), and then it can be decoupled to get m+n+p decoupled differential equations whose i‐th element is shown as follows

with i = 1, 2, …, m + n + p . Three distinct situations are given according to the sign of emax(0).

· For emax(0) ＞0, note that for any given i, emax(0) ≥ei(0).Thus it is easy to get ei(t) ≤emax(t) and - emax(t) ≤ei(t), ∀i.Then it can be concluded that-emax(t)≤ei(t)≤emax(t)for∀i,from which it is ensured that as emax(t)approaches 0,ei(t)also comes to 0 for ∀i. Thus, it is concluded that the maximum convergence time depends on the value of emax(t).In other words, tc≤tmaxwhere tmaxis the time it takes for emax(t)to converge to zero.According to Equations(8)and(11), the following equation is derived to get tmax:

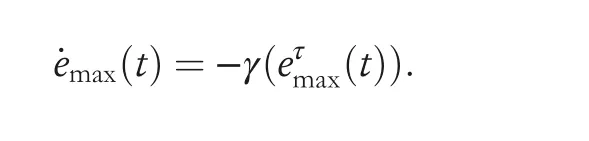
Thus it has

《宪法》第33条第2款规定：“中华人民共和国公民在法律面前一律平等。”这一条款被认为确立了作为基本权利的“平等权”。作为社会主义国家的“平等权”，我国《宪法》中的平等权在机会平等之外更强调条件平等，机会平等反对任何差别，对一切公民一视同仁，而条件平等承认合理差别，根据公民自身的特点，提供不同的条件。旨在减少收入分配两极分化的社会救助权即体现了这种条件平等。同时，在社会救助权内部，基于地域间的经济差异，公民所能够请求的救助水准也有不同；基于个体情况的差异，公民所能够请求的救助内容也有不同。这种看似“不同”的救助实则体现了社会救助权“条件平等”的内涵。

3.3 | ZNN model with combined activation function

Although SSZNN model(12)converges faster than SBPZNN model (6) and is able to be convergent in finite time, its convergence time is too heavily influenced by |emax(0)|. That is,the convergence time would be dramatically extended in the case of a large difference between theoretical solutions of the problem and neural states of SSZNN model (12) at the beginning.For this unsatisfactory factor,we have the following combined activation function:

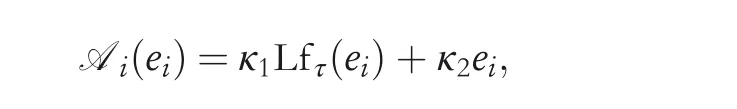
which is generated through linearly combining activation function (11) with coefficient κ1and the linear activation function with coefficient κ2. So the following modified ZNN model named the CZNN model is derived by exploiting the activation function above:

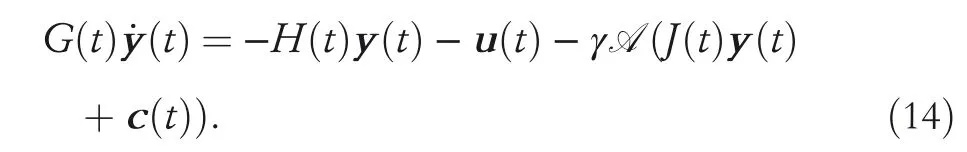
γκ1and γκ2are replaced with ν1and ν2, respectively. For studying the convergence of CZNN model(14),the following theorem is thus presented.

Theorem 4 CZNN model (14) converges to the theo‐retical solution y*(t) of Equation (2) in finite time tc,and the first n members of y*(t) are the optimal so‐lution to TVQP problem (1) with

where emax(0) is the one possessing the maximum absolute value among all elements of the vector e(0) = J(0)y(0) + c(0).

Proof. Rewriting CZNN model (14) leads to ˙e(t)=-γA (e(t)),then it can be decoupled to get m+n+p decoupled differential equations whose i-th element is shown as follows:

with i = 1, 2, …, m + n + p . Similarly, three distinguishing situations are analysed in detail in the following part.

· For emax(0) ＞0, we have

· For emax(0)＜0,similarly to the situation of emax(0)＞0,the result is also generalised as

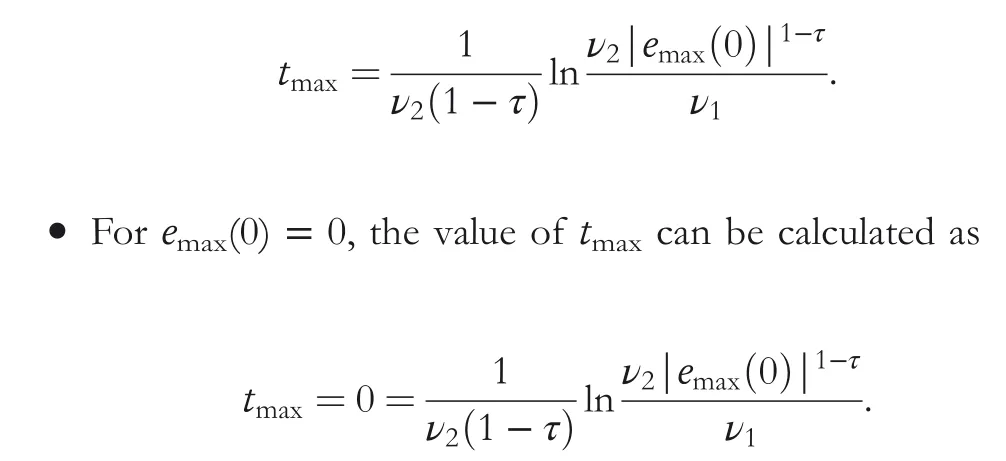
At this point,the whole proof on its finite-time convergent performance of CZNN model(14)in solving TVQP problems is completely done.

3.4 | ZNN model with saturation activation function

Note that most of the existing ZNN models are not saturated,a saturation function is offered, which is displayed as follows:

Furthermore, the corresponding SZNN model is established and shown as

To simplify the proof process of the theorem, for all elements of the bound,the values are set to be the same as η1with η1＞0,and then analysing the convergence property of SZNN model(17)can be done by investigating the following theorem.

Theorem 5 SZNN model (17) converges to the theo‐retical solution y*(t) of Equation (2) in finite time tc,and the first n members of y*(t) are the optimal so‐lution to TVQP problem (1) with

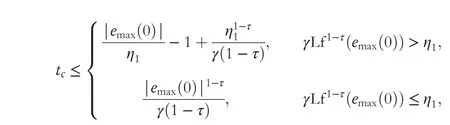
where emax(0) is the one possessing the maximum absolute value among all elements of the initial vector e(0) = J(0)y(0) + c(0).

Proof. Rewriting SZNN model (17) leads to ˙e(t)=-γC(e(t)),then we can decouple it to get m+n+p decoupled differential equations whose i-th element is shown as follows:

By adding up the two values of time t obtained above,the following is found

· For γLfτ(emax(0)) ≤η1, it can similarly be derived that

Therefore,the proof on SZNN model(17)for finding the solution to the TVQP problem is completed.

4 | NUMERICAL SIMULATIONS

To enable the ZNN method to better solve TVQP problems,four modified ZNN models are proposed, that is, NPZNN model (10), SSZNN model (12), CZNN model (14) and SZNN model (17), respectively. In this section, computer simulations of these four ZNN models for solving TVQP problems are presented to make comparisons among these diverse models and to verify their effectiveness.

Consider the following benchmark TVQP problem with equality and inequality constraints investigated in [32]:

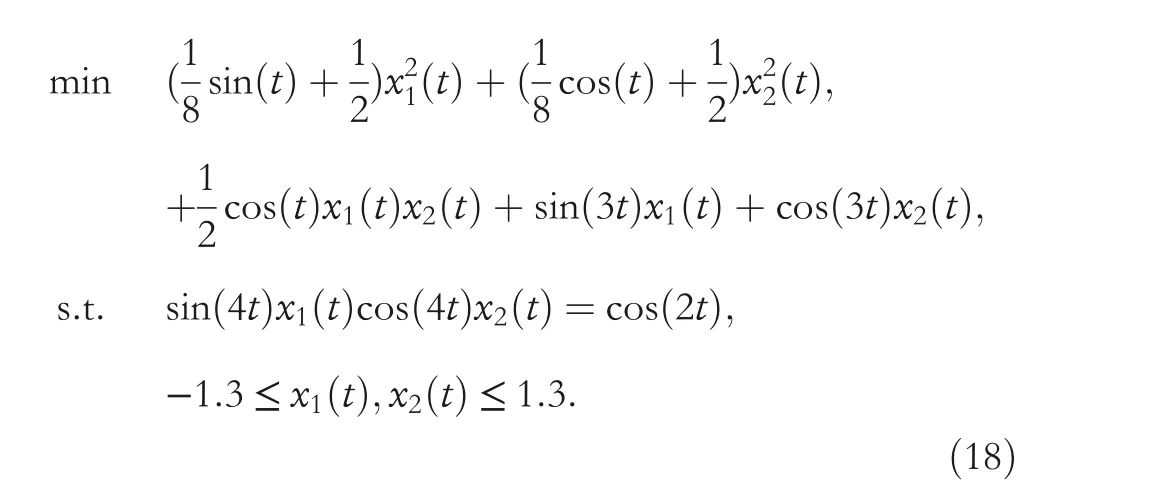
Reformulate (18) as the standard form of TVQP problem shown in (1), and then coefficient matrices are obtained as

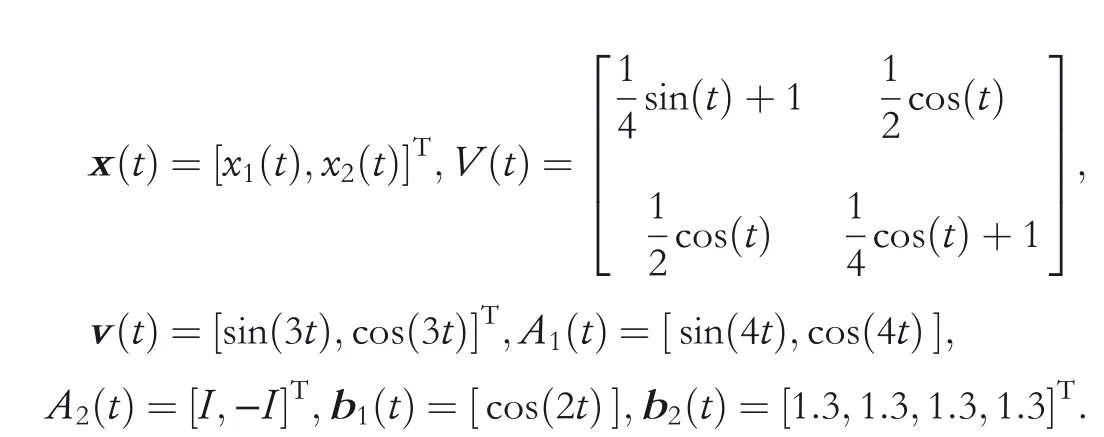
Through the observation, the proposed ZNN models are all designed as ordinary differential equations(ODEs).For the solutions to these special equations,the ODE solver in Matlab is utilised in the simulation experiment.

4.1 | ZNN with accelerated finite‐time convergence

In this section, the convergence properties of SBPZNN model (6), SSZNN model (12) and CZNN model (14) are studied. The original ZNN model in [24] and GNN model in[30] are also used for comparative analysis and verification.Simulative results are illustrated in Figure 1 with the parameters chosen as γ = 2 and the initial values set as zero. The processes of neural states converging to the theoretical solutions are shown in Figure 1a,b, respectively, from which it can be seen that, under similar conditions, the state trajectories of ZNN models begin to overlap soon (less than 6 s),while that of the GNN model always lags behind. Such a result preliminarily shows that both modified ZNN models and the original ZNN model [24] are more accurate and effective in solving TVQP problems compared with the GNN model in [30]. In Figure 1c, in addition to the ZNN model [24], the residual errors of ZNN models are able to converge to zero within 3 s, substantiating the properties of finite-time convergent previously proved. Moreover, it is revealed in Figure 1c that proposed SSZNN models (12) and CZNN models (14) converge faster than the traditional SBPZNN model (6), with the CZNN model (14) being the fastest, which is also consistent with the previous theorems and reflects the superiority of the new models. Furthermore,comparisons among these diverse models are summarised in Table 1.

4.2 | ZNN with non‐convex functions

4.2.1 | Convergence with bound constraints

In this simulation, η-and η+are set as 1 and –1, respectively, and the initial state consists of m + n + p random numbers. The corresponding results are displayed in Figure 2. As can be seen from Figure 2a, the residual error of NPZNN model (10) approaches 0 over time, verifying the global convergence of this model. Besides, as visualised in Figure 2b, ˙ei(t)=1 is obtained in the case ei(t) ＞1 and ˙ei(t)=-1 is obtained in the case that ei(t) ＜- 1, from which it can be deduced that NPZNN model (10) satisfies the bound constraint.

4.2.2 | Convergence with ball constraints

With R =1 selected and initial states randomly generated, the simulation result in this case is displayed in Figure 3. It is evident that the residual error‖e(t)‖2is of global convergence,which indicates that NPZNN model (10) with ball constraint on activation functions is also feasible to solve TVQP problems.

4.2.3 | Convergence with non-convex constraints

The following non-convex set is adopted for the simulation to verify the effectiveness of NPZNN model (10) with nonconvex constraint on activation functions for solving TVQP problems:

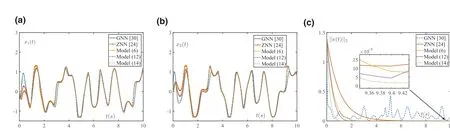
FIGURE 1 Comparisons of GNN [30], ZNN [24], SBPZNN model (6), SSZNN model (12) and CZNN model (14) for solving a TVQP problem (18)[:(a)neural state x1(t);(b)neural state x2(t);(c)residual error‖e(t)‖2.GNN,gradient neural network;SBPZNN,sign-bi-power ZNN model;TVPQ,time-variant quadratic programming; ZNN, zeroing neural network

TA B L E 1 Comparisons among different models

By using set Ω, simulation results are acquired in Figure 4. As indicated in Figure 4a, the residual error gradually converges to zero over time. Also, Figure 4b shows that since the initial residual error is large, the elements of ˙e(t) are either 1 or –1. Over time, the elements of ˙e(t) decreased in a limited range [-0.1, 0.1] and remain thereafter, indicating that the non-convex sets can also serve as the activation functions to increase the converging rate of NPZNN model (10).

4.3 | ZNN with saturation functions

With η1=2 selected,the simulation results of the ZNN model with saturation function are displayed in Figure 5. It is illustrated in Figure 5a that the residual error‖e(t)‖2converges to zero within 2 s. Also, as revealed in Figure 5b, the element values in the change rate vector ˙e(t) are within the range [–2,2]. The two results substantiate the finite-time convergent property and saturation property of SZNN model (17)separately.

FIGURE 2 Convergence of NPZNN model(10)with bound constraint for solving problem(18):(a)residual error‖e(t)‖2;(b)error derivative vector ˙e(t)

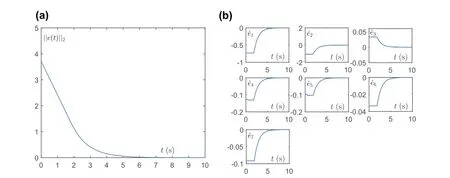
FIGURE 3 Convergence of the NPZNN model(10)with ball constraint for solving problem(18):(a)residual error‖e(t)‖2;(b)error derivative vector ˙e(t)

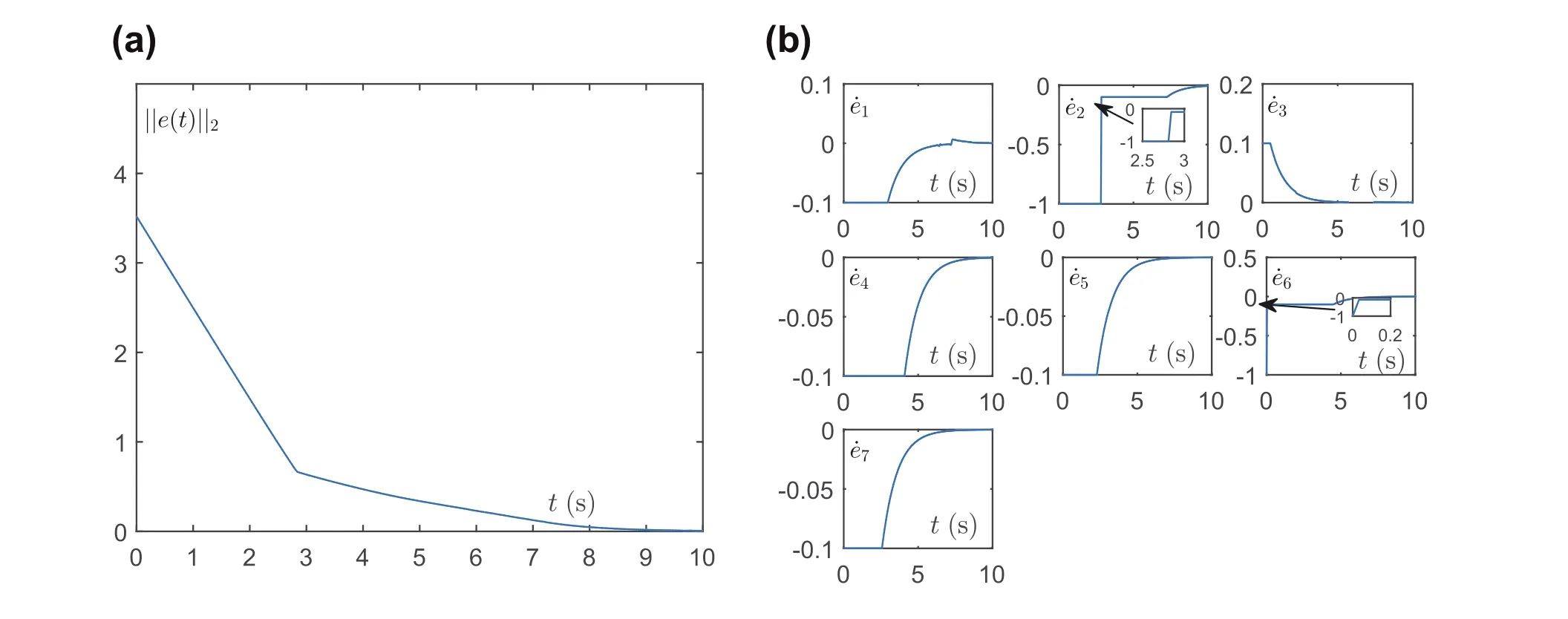
FIGURE 4 Convergence of the NPZNN model (10) with non-convex constraint for solving TVQP problem (18): (a) residual error ‖e(t)‖2; (b) error derivative vector ˙e(t)

FIGURE 5 Convergence of SZNN model(17)with saturation function for solving problem(18):(a)residual error‖e(t)‖2;(b)error derivative vector ˙e(t)

5 | CONCLUSION

The authors have investigated the existing ZNN models for solving TVQP problems at the start and then discovered two limitations, that is, the low convergence speed resulting from redundant formulation of activation function and unnecessary convex restriction on activation function, respectively. By proposing NPZNN model (10) with non-convex-allowed activation functions, the first limitation is overcome. Meanwhile, SSZNN model (12) and CZNN model (14) with accelerated finite-time convergence properties have been proposed to overcome the second limitation. It is indicated in the theoretical derivations and simulation results that the modified ZNN models are able to solve TVQP problems better and accurately. In addition, new ZNN models with improved performance for solving TVQP problems as well as their practical applications are expected to be further investigated.

ACKNOWLEDGEMENT

This work was supported in part by the National Key Research and Development Program of China (No. 2017YFE0118900),in part by the research project of Huawei Mindspore Academic Award Fund of Chinese Association of Artificial Intelligence(No.CAAIXSJLJJ-2020-009A),in part by the Team Project of Natural Science Foundation of Qinghai Province, China (No.2020-ZJ-903), in part by the Natural Science Foundation of Gansu Province, China (No. 20JR10RA639), in part by the Natural Science Foundation of Chongqing (China) (No.cstc2020jcyj-zdxmX0028), in part by the Research and Development Foundation of Nanchong (China) (No.20YFZJ0018),in part by the Project Supported by Chongqing Key Laboratory of Mobile Communications Technology (No.cqupt-mct-202004), and in part by the Fundamental Research Funds for the Central Universities (No. lzujbky-2019-89).