高 健，许文杰，欧宜贵

（海南大学理学院，海南海口 570228）

最短路问题，一般来说就是从给定的网络图中找出给定的起点和终点之间距离最短的一条路径.这里所说的“距离”只是权数的代称，可以是通常说的距离，也可以是时间、费用等.

众所周知，最短路问题不仅在生产管理、交通运输和通讯领域具有广泛的应用，而且经常被作为一个基本工具，用于解决其他优化问题［1-2］.因此，此类问题吸引了众多研究人员对其求解算法进行探讨.迄今为止，求最短路问题的主要经典算法有Bellman-动态规划算法、Dijkstra算法和Floyd算法［1］.需要指出的是，这些经典的数值算法属于离散化的迭代方法，一般只能处理小规模的问题，而对较大规模的问题以及需要实时解的问题（比如业务路由选择问题和路线规划问题［3-4］）就会失效，甚至无能为力.这是由于求解此类优化问题的运行时间主要依赖于问题的维数和结构以及所用优化算法的复杂性.为了克服这些缺陷，一种结合神经网络和动力系统（一般由一阶微分方程表示）的神经动力系统模型优化方法［5-6］应运而生.

基于神经动力系统模型的优化方法是近三十多年发展起来的一类优化方法［6］.以光滑优化问题为例，这类方法的本质是：基于原始优化问题构造某一常微分方程系统，使得该系统的平衡点对应于原问题的最优解，然后再选取适当的数值方法来求解该微分方程系统，从而获得原优化问题的最优解或近似最优解.引入微分方程的魅力在于能帮助研究者系统地研究微分系统解的瞬态性能和极限行为，从而追踪从初始点到极限点之间的连续运动轨迹.由于此类优化方法兼顾了经典的动力系统和神经网络2种方法的优点（即大规模并行计算和分批处理信息的能力以及解的实时在线特性），同时在分析动力系统的稳定性时采用了不同以往的新策略，从而可能避免使用传统的Lyapunov函数，使得在利用这类新方法来研究最优化问题时获得了较先前更好的理论结果以及更具竞争力的数值表现性能.目前，基于神经动力系统的优化方法已取得了若干重要进展［6-10］.

最近，已有学者研究并提出了求解最短路问题的神经动力系统模型优化方法［11-14］.但是这些方法的模型结构复杂，且不容易实施.因此，如何构造结构简单、稳定性好且容易实施的神经动力系统模型来处理这类特殊优化问题就显得非常必要.

基于上述讨论，并受文献［8，11，15］的启发，笔者提出了一个基于神经动力系统模型的求解最短路问题的优化方法，其基本思想：先将最短路问题转化为线性规划（LP）模型，再利用该LP模型来构造结构简单且容易实施的神经动力系统模型（理论上可以证明该模型的平衡点等价于LP的最优解），最后通过求解所提出的系统模型来得到最短路问题的最短路径和最短路长.

1 最短路问题的LP模型

为讨论问题的方便，只考虑含有n个顶点的有向赋权图，且假设所考虑的图没有负回路［1］.

给定一个赋权有向图G=(V，A，W)，其中V是含有n个顶点的集合（记为V={v1，v2，…，v n}），A是具有m条弧的集合（记为A={e1，e2，…，e m}），而W=(w ij)为图G的所有弧的权集合（也称为权矩阵，而wij表示弧(v i，v j)≜(i，j)的权数）.又给定G中的一个起点v s和一个终点v t，并设P是G中从v s到v t的一条路，则定义路P的权是P中所有弧的权之和，记为w(P)，即

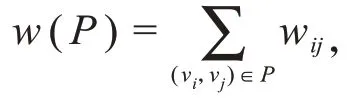
又若P*是图P中从v s到v t的一条路，且满足：对G中所有从v s到v t的路P，均有

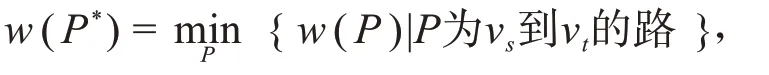
则称P*为从v s到v t的最短路，w(P*)为从v s到v t的最短距离.在一个图G=(V，A，W)中，求从v s到v t的最短路和最短距离的问题就称为最短路问题.

为了建模的方便，不妨设图G=(V，A，W)中的起点v s和终点v t分别是1和n.引入0-1整数决策变量x ij，其定义

于是，最短路问题的LP模型就可表示为

且满足

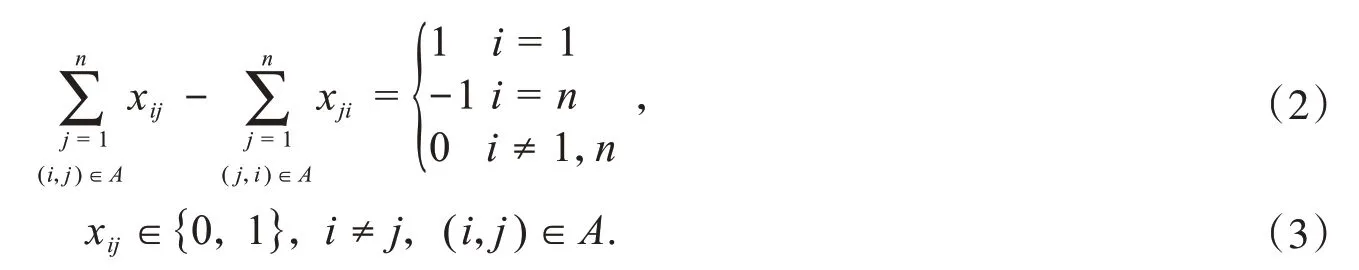
对于上述LP模型，由于式（2）中定义的等式约束的系数矩阵具有全幺模性［2］，那么在最短路径唯一的条件下，0-1整数性约束（3）可以等价地被替换为非负性约束.换言之，如果最短路问题存在唯一最优解，则上述整数线性规划问题（1）～（3）的最优解总是由数0和1构成的［2］.最短路问题可以通过下列等价的LP来求解

且满足

其中，δij表示Kroneckerδ函数，其定义是

基于上述讨论，可以得出：最短路问题可转化为一类LP问题（4）～（6）.因此，考虑比上述LP问题更一般的LP问题

其中，A∈R m×n，b∈Rn，c∈Rn，x∈Rn，且rankA=m.问题（7）的对偶问题是

2 最短路问题的神经动力系统模型

为了定义最短路问题的神经动力系统模型，给出下列定义.

设Ω是Rn上的非空闭凸集.对于任意给定的v∈Rn，v在Ω的投影PΩ(v)定义为

特别地，如果Ω={x∈Rn|l≤x≤u}，有

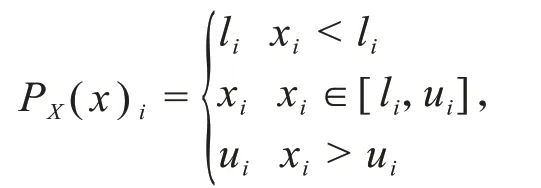
其中，(x)i表示向量x∈R n的第i个分量.

类似于文献［15］中的讨论，可以得到求解LP问题（7）和（8）的神经动力系统模型

其中，X={x∈Rn|x i≥0，i=1，2，…，n}，ε＞0是时间控制参数，而y∈Rn是对偶变量.显然，当ε=1时，模型（10）就是文献［15］中模型.

关于神经动力系统模型（10）的稳定性，有如下结论.

定理1神经动力系统模型（10）的解轨迹z(t)=(x(t)，y(t))T全局收敛于问题（7）和（8）的精确解z*=(x*，y*)T.

证明类似于文献［15］中定理3.3的证明方法可得证，在此略去.

注1 若将LP问题（7）～（8）中的非负约束x≥0看成不等式约束，则类似于文献［16］中的讨论，可以得到LP问题（7）～（8）的另一个神经动力系统模型

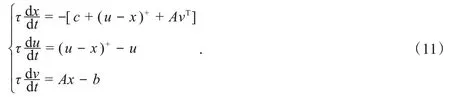
显然，模型（11）具有2n+m个状态变量，而模型（10）具有n+m个状态变量.因此，同模型（11）相比而言，模型（10）的计算量更少，且更易实施.

3 数值模拟实验

为了验证神经动力系统模型（10）的表现性能，选取了2个实例［17］来进行数值模拟测试，在实验过程中，采用Matlab的常微分方程求解器是ODE23.

问题1 求图1中的顶点V1到V7的最短路径.

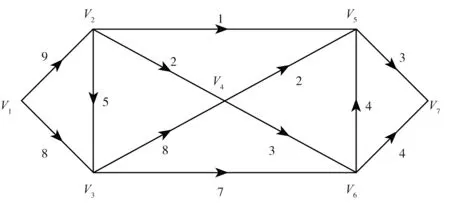
图1 顶点V1到V7的路径图

此问题可表示为下列0-1整数线性规划模型

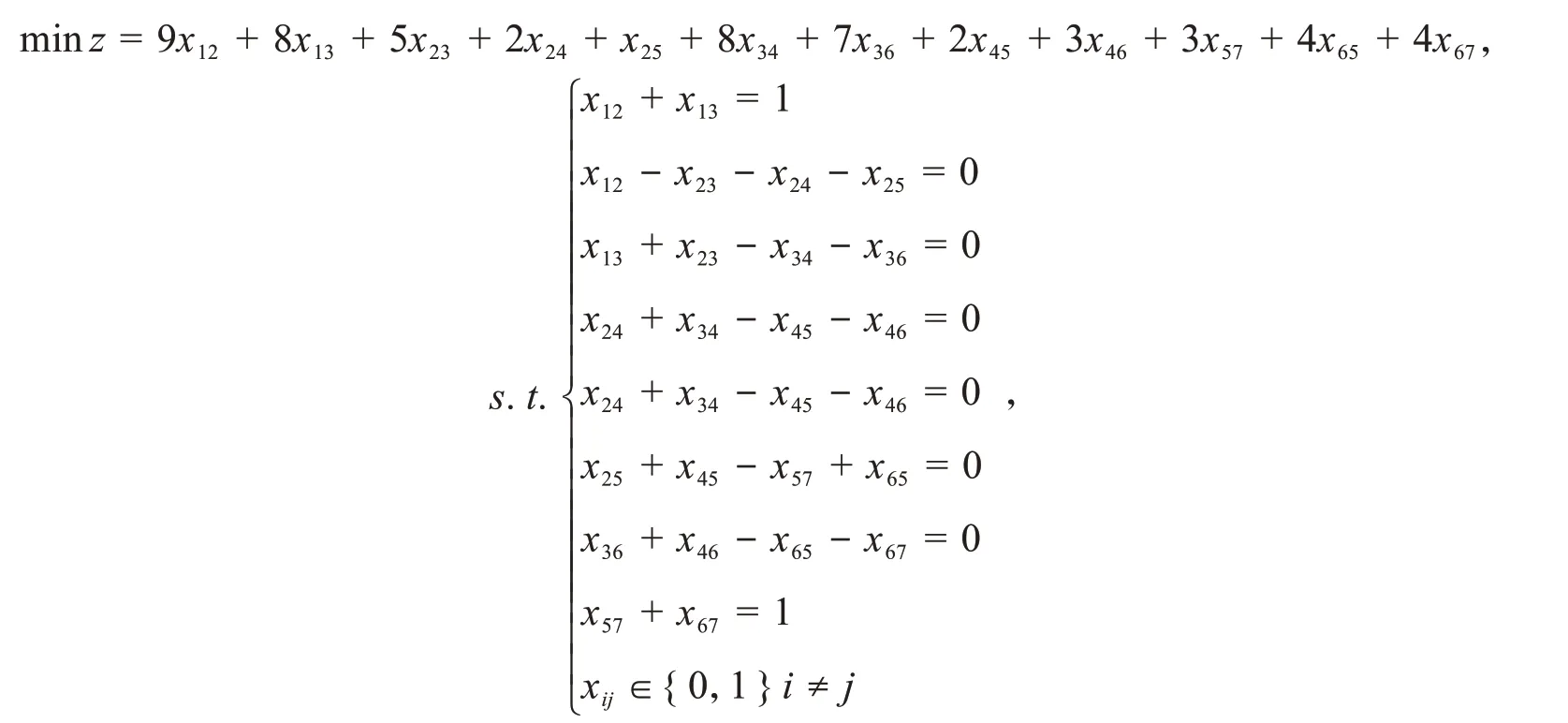
按上一节的讨论，可简化为

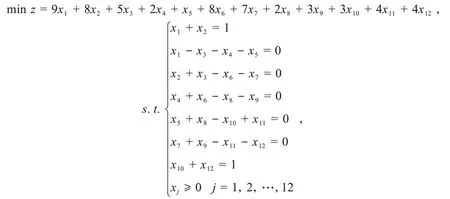
其中，x1=x12，x2=x13，x3=x23，x4=x24，x5=x25，x6=x34，x7=x36，x8=x45，x9=x46，x10=x57，x11=x65，x12=x67.

此问题有最短路径：V1→V2→V5→V7.在［0，1］随机产生初始点x10，其模拟结果如图2所示.图3给出了误差‖x(t)-x*‖对初始点x10的收敛性.

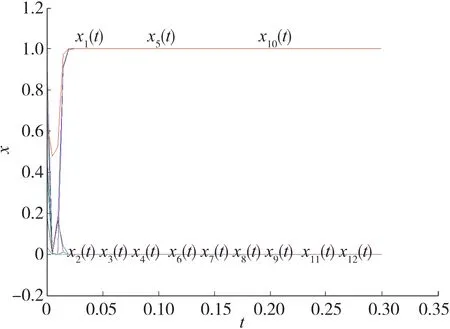
图2 例1中x（t）对初始点x01的瞬态行为

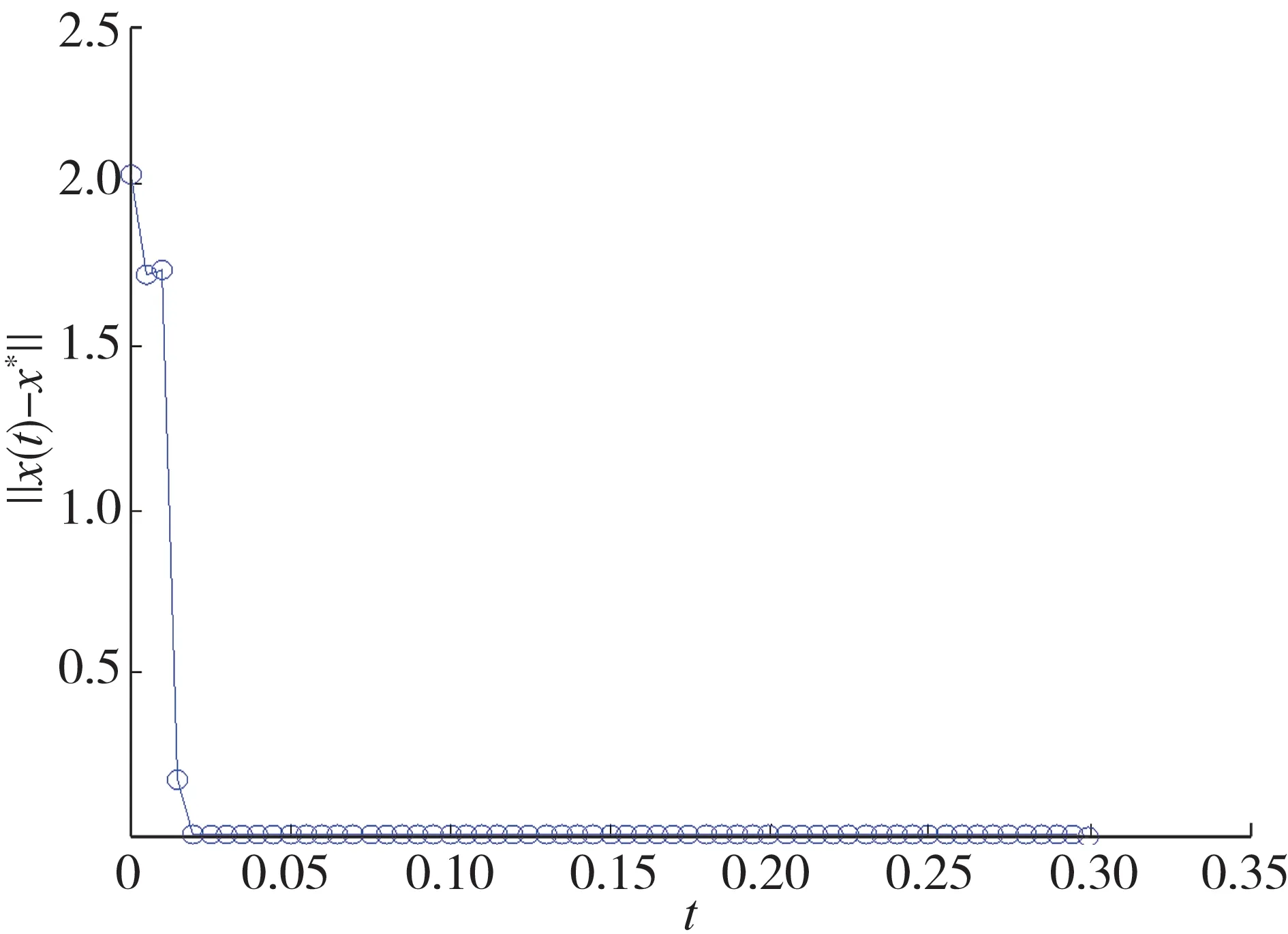
图3 例1中误差‖x(t)-x*‖对初始点x01的收敛性

问题2 求图4中的顶点V1到V9的最短路径.

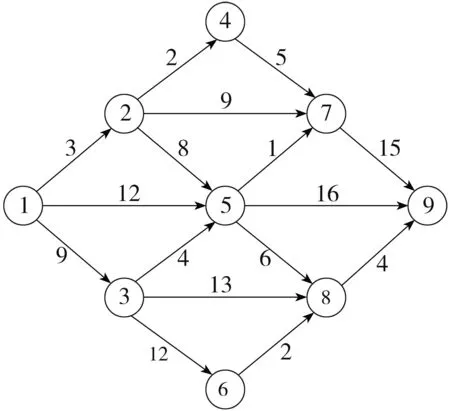
图4 顶点V1到V9的路径图

此问题可表示为下列0-1整数线性规划模型

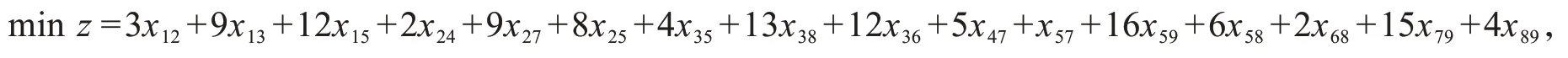
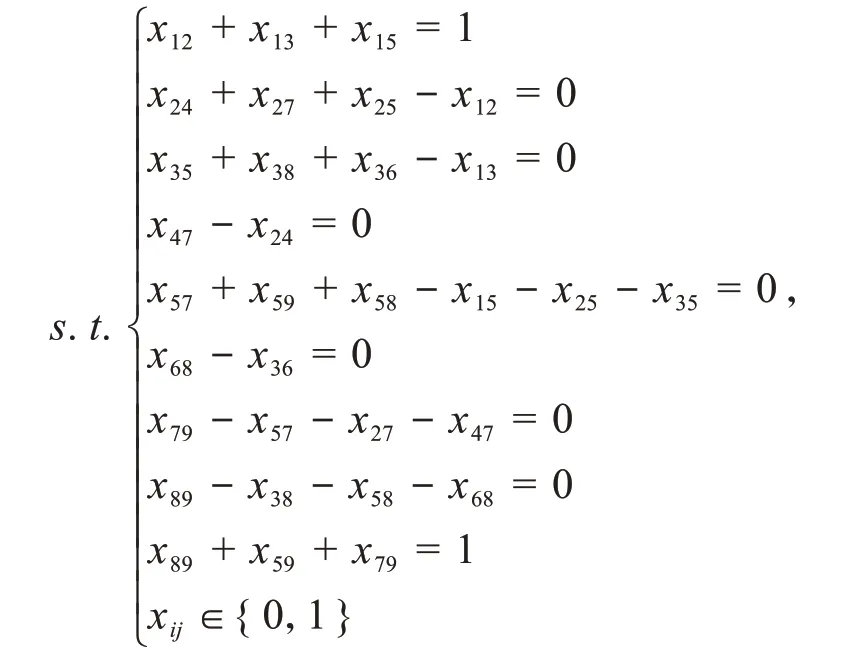
可简化为

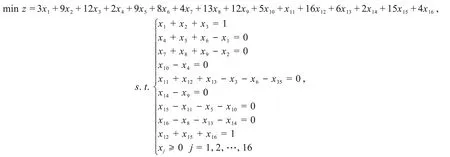
其中，x1=x12，x2=x13，x3=x15，x4=x24，x5=x27，x6=x25，x7=x35，x8=x38，x9=x36，x10=x47，x11=x57，x12=x59，x13=x58，x14=x68，x15=x79，x16=x89.

此问题有最短路径：V1→V2→V5→V8→V9.在［0，1］随机产生初始点x20，其模拟结果如图5所示.图6给出了误差‖x(t)-x*‖对初始点x20的收敛性.

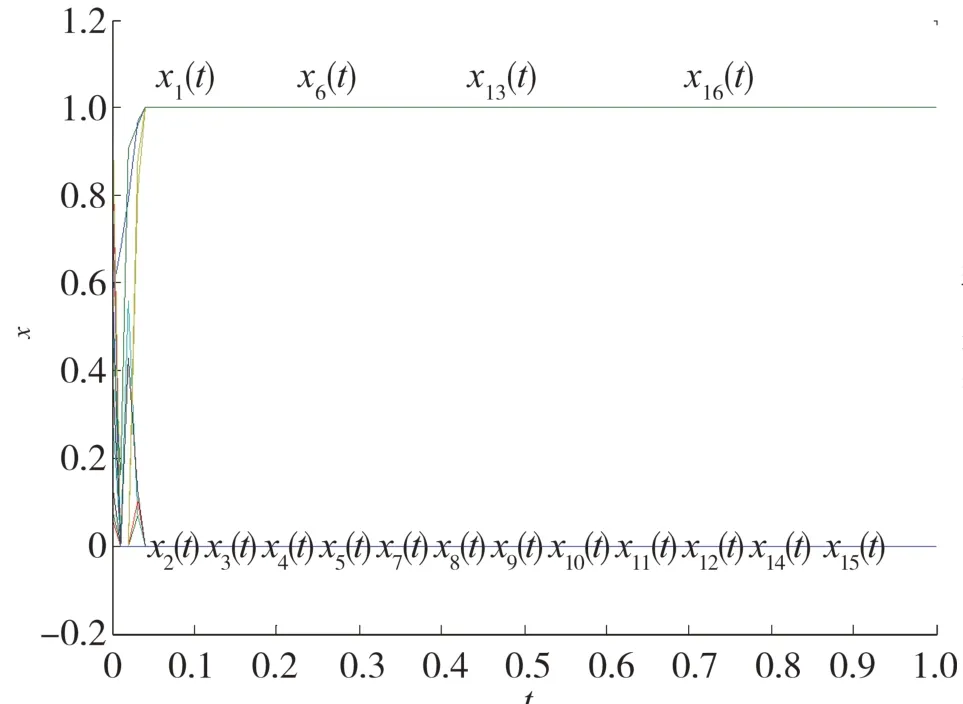
图5 例2中x（t）对初始点x02的瞬态行为

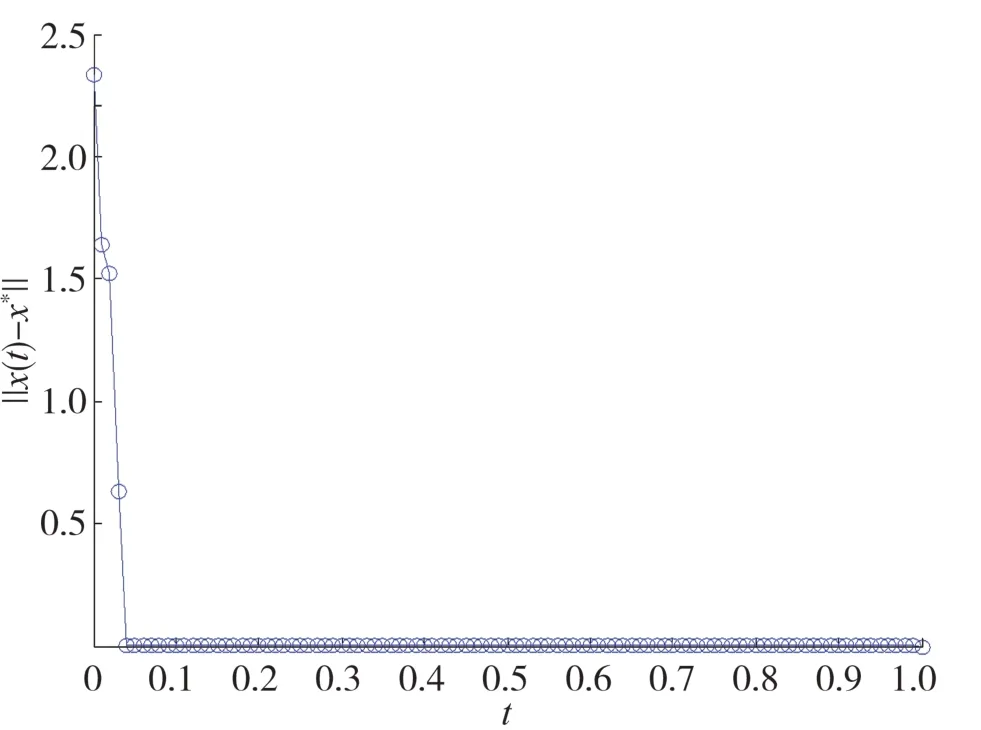
图6 例2中误差‖x(t)-x*‖对初始点x02的收敛性

尽管从这有限的2个实例得不到一般性的结论，但从图2和3以及图5和6可以看出：神经动力系统模型（10）能比较有效地求出网路图的最短路径.

4 结束语

给出了一个基于神经动力系统模型的求解最短路问题的连续化优化方法，并得到其全局稳定性结论.2个具体的数值模拟结果验证了该方法的可行性.本文所得到的结果对解决工程中的最短路径问题具有比较重要的理论价值.利用本文所提出的连续化优化方法来解决较大规模的最短路问题并检验本文所提出方法的实践价值是下一步工作的重点.