冯青松 杨 舟 郭文杰,2) 陆建飞 梁玉雄

*(华东交通大学铁路环境振动与噪声教育部工程研究中心,南昌 330013)

†(江苏大学土木工程与力学学院,江苏镇江 212013)

引言

周期结构因其具有良好的弹性波衰减特性[1-2](带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力.近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3]、板结构[4-5]拓展到复杂的三维结构[6-7].与此同时,作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点,大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8-9]、磁流变材料[10]、功能梯度材料[11]等) 和弹簧-振子系统[12-15]引入周期结构中,以实现带隙的主动调控和带宽的增大,并取得了很好的效果.

在过去的几十年里,学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16-19]作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力.但是,有限元方法的精度依赖于离散单元的网格尺寸,高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算,为提高传统有限元法的计算效率,提出了一些新的数值方法,如波动有限元法[20-21],并将其迅速推广到超材料杆[22]、多孔板[23]、周期性加筋壳[24]等结构的带隙计算之中.但是无论从检验数值法的角度,还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25-26]、平面波展开法[27-28]等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29-30].对于一维结构,传递矩阵法是一种通用的方法,但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解,因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难.此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31]、小波法[32]、渐进匹配展开法[33]等,这些方法虽各有特点,但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此,有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法.

能量法具有将求解微分方程边值问题转化为泛函极值问题的优点,这有利于复杂结构系统耦合问题的求解,因而传统能量法(如Rayleigh-Ritz 法[34-35])被广泛应用于分析一些复杂组合结构的自由振动问题[36-37],近年来也被引入周期结构带隙计算中[38-39].但在利用传统能量法计算周期结构带隙时,存在如下问题:(1) 能量法需要基于Bloch 定理构造满足周期性边界的位移场形函数[40-41],从数学角度而言,形函数的周期性重构难度较大,而且不同形函数的构造方式不一定相同;(2)重构以后的位移场形函数包含波数,这会导致涉及形函数的结构的质量和刚度矩阵中含有波数,在计算带隙时,结构的质量和刚度矩阵需随着波数的变化进行反复计算,随着结构质量和刚度矩阵维度的增大,或者扫描波数点数的增多,计算成本也会随之增大.因此,对于能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作.

鉴于此,本文对传统能量法进行了改进,提出了一种利用人工弹簧[42-44]来模拟周期边界条件的方法,将形函数与周期边界条件分离,无需构造满足周期边界的形函数,这样可解决传统能量法中构造满足周期边界条件的形函数的困难问题;同时,利用人工弹簧模拟周期边界条件,将周期边界约束转化为人工弹簧的弹性势能,这样只有包含波数的周期边界弹性势能矩阵需参与随波数扫描的循环计算,其他矩阵只需计算一次,因而能提高传统能量法计算带隙的效率.此外,人工弹簧模型使用灵活、便捷,可进一步拓展到更为复杂的周期性组合结构的带隙分析中.

1 人工弹簧模拟周期边界的基本原理

1.1 问题陈述

以图1 所示周期性薄板为例,对引言中提到的传统能量法计算周期结构带隙时存在的问题进行具体阐述.

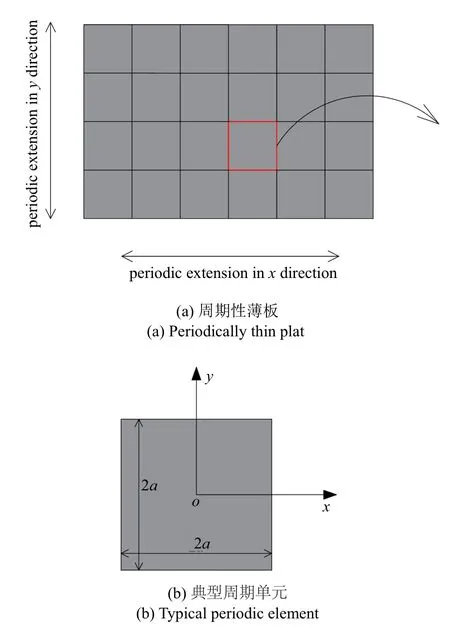
图1 周期性薄板自由振动分析模型Fig.1 Vibration analysis model of a periodically thin plate with free boundary

对于图1 所示的周期薄板结构,取出一个周期单元进行分析.根据Kirchhoff-Love 薄板理论,平面内位移u和v可以通过一阶泰勒级数围绕中面层展开,表示为平面外位移w,位移向量可以表示为

将式(1)中的横向位移w表示为基函数ξi(x,y)和一个未知的权重系数di(t)的组合,即

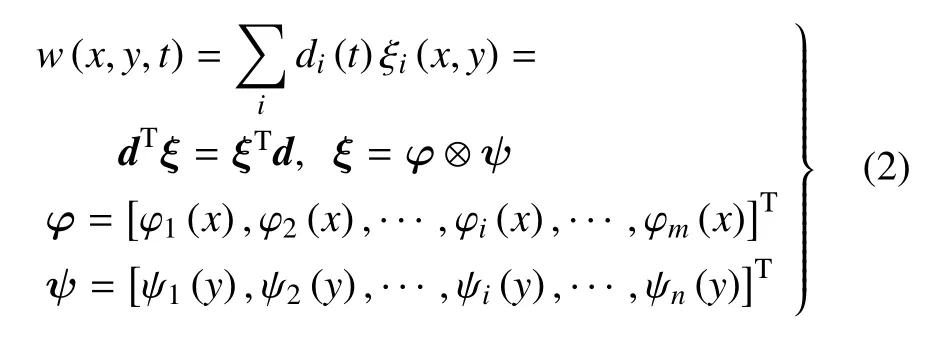
式中,符号⊗表示克罗内克积.

根据Bloch 定理,周期单元在x,y方向上的位移、转角、弯矩和剪力需要满足Bloch 周期性边界条件,即

式中,kx,ky表示沿着x,y方向的波数.方程(3)～(6)要求式(2)中的形函数ξi(x,y)满足Bloch-Floquet 周期性条件.从数学角度而言,形函数的重构过程具有相当大的难度,且不同的形函数构造方式不一定相同,这给利用传统能量法求解周期结构振动带隙问题带来了困难.

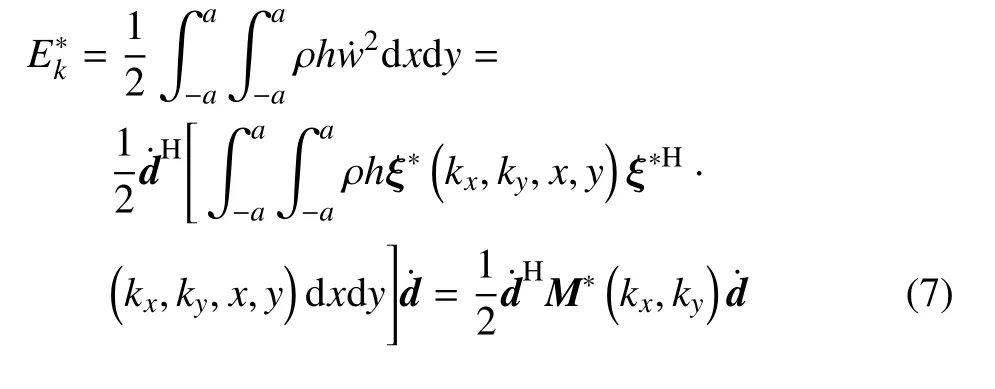
其中,ρ,h,ν 分别表示板的材料密度、板的厚度以及板材料泊松比;D=E*h3/[12(1-ν2)]表示板的抗弯刚度.由式(7)、式(8)可以得到周期单元的整体拉格朗日量

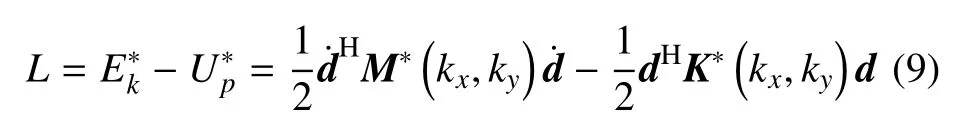
进一步地,定义未知的与时间相关向量d(t)=结合Eular-Lagrange 方程

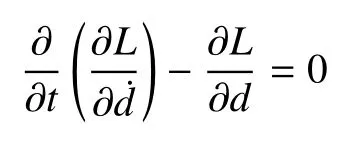
就能导出周期薄板结构的运动方程

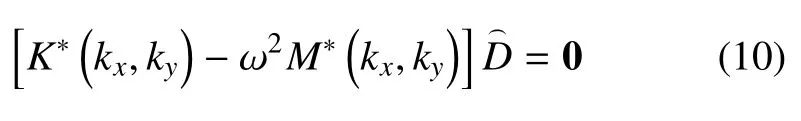
式(10) 是一个标准的特征值方程问题,在第一布里渊区kx×ky=[-π/a,π/a]×[-π/a,π/a]扫描波数,即能得到周期薄板结构弯曲振动的频散曲线.值得注意的是,由于重构以后的形函数必然包含波数,这就导致利用位移形函数表征的结构动能表达式(7)和应变能表达式(8)中也含有波数,进而使得薄板结构运动方程(10)中的质量矩阵刚度矩阵同样包含波数.因此,在扫描波数进行带隙计算时,结构的质量和刚度矩阵需要随着波数的变化进行循环计算,计算时间会随着结构的质量和刚度矩阵维度以及扫描波数点数的增大而呈倍数增大,计算成本也会急剧增大.因此,如上所述,对于传统能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作.

1.2 人工弹簧模拟周期性边界条件

尝试将特殊的周期性边界条件与位移形函数完全分离,即无需对形函数进行重新构造,用人工弹簧的形式来模拟周期性边界条件.如图2 所示,在周期单元的4 条边界处定义线弹簧和转角弹簧两类弹簧,它的物理意义是在x和y两个方向通过人工弹簧将上一周期单元的尾端与下一周期单元的首端相连.文献[3]证明了,只需要位移和转角满足周期性条件,解即收敛于真实解.

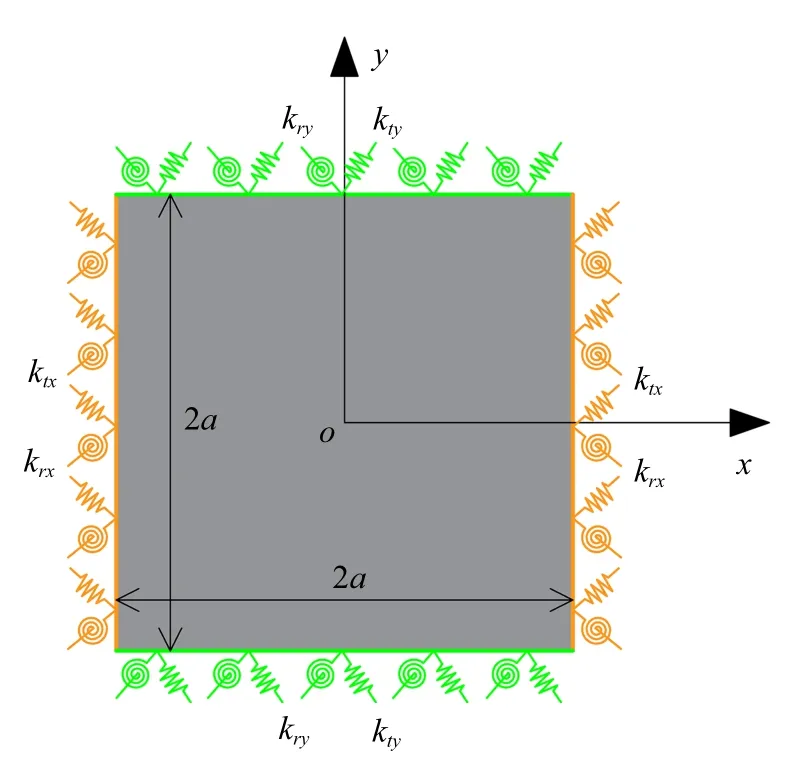
图2 人工弹簧定义周期性边界的分析示意图Fig.2 Analysis schematic diagram of periodic boundary defined by artificial spring

以x方向为例,此时边界势能可以表示为

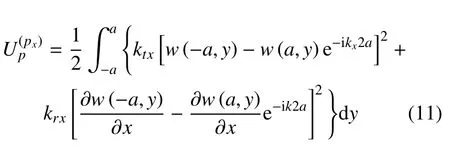
式中w(-a,y)-w(a,y)e-ikx2a,∂w(-a,y)/(∂x)-[∂w(a,y)/(∂x)]e-ik2a分别表示第一个周期首端与第二个周期首端的位移、转角差值.同时,由式(3)、式(4)可知位移和转角的差值趋于0,即

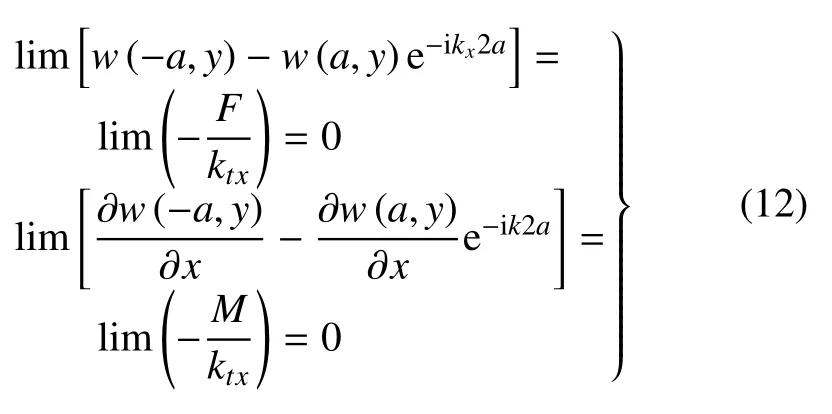
结构的剪力和弯矩都是一个有限值,因此式(12) 若要成立,则需要满足limktx=∞,limktx=∞,同理考虑y方向的周期性边界,式(11)改写为

在式(13) 中,周期性边界条件表示为包含波数在内的弹性势能的形式,与位移形函数分离.此时,形函数ξi(x,y) 无需进行构造以满足周期性边界,周期单元的动能和应变能表示为

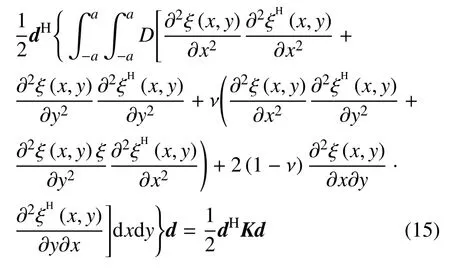
进一步地,周期单元的整体拉格朗日量表示为

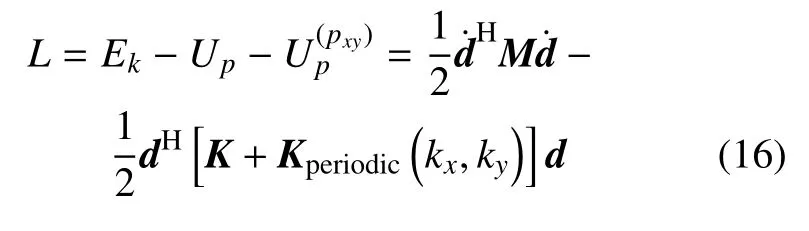
结合前述定义的与时间相关未知向量d(t)=以及Eular-Lagrange 方程

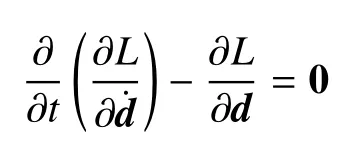
式(10)中周期薄板结构的运动方程改写为

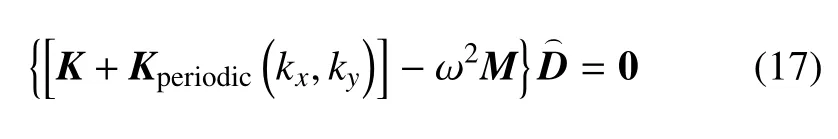
通过比较方程(14) 和(15) 与方程(7) 和(8) 可以发现,利用人工弹簧模拟周期性边界,将位移形函数与周期性边界条件分离,选取的形函数无需满足周期性边界,进而用形函数表征的结构动能和应变能表达式中没有包含波数,同时通过对比最后的特征值方程(17) 和(10) 可以看出,仅有周期边界势能刚度矩阵中包含波数,质量与应变能刚度矩阵中都不包含波数,在扫描波数进行求解时,除了周期边界弹性势能矩阵参与波数扫描循环计算,其他的矩阵仅需计算一次,这将大幅度提高计算效率,进而降低计算成本.后续的算例验证中,将进一步证明本文方法的准确性和效率性.

2 算例验证:周期开口板弯曲振动带隙计算

开口板广泛应用于土木、船舶等结构中.开孔板的振动在能量传递中起着重要作用,但也与辐射噪声对周围环境的影响有直接关系.因此,本节以周期开口板为例,验证人工弹簧模拟周期性边界的准确性,同时说明该方法与传统能量法相比,在计算效率上的优势性.

2.1 位移形函数的选取及特征值方程求解

由于开口板出现了局部厚度突变,若选用改进傅里叶级数、切比雪夫级数等(适用于描述连续性较好的结构) 作为位移形函数可能需要多项级数来进行拟合以达到精度要求,进而降低计算效率.因此,本文选取具有局域化特性的高斯小波函数[45-46]为位移形函数,以确保能够准确捕捉到厚度变化区域的波动特征,即对于式(2)定义

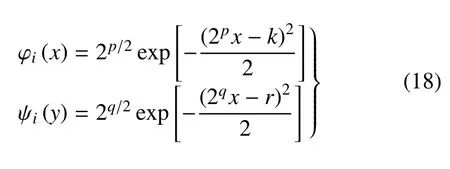
式中,p,q和k,r分别表示伸缩因子和平移因子.伸缩因子p,q控制着解的精度,采用越大的尺度因子使得形函数具有更高的分辨率,进而能更精确地模拟更高频的波场,但同时要求更多的计算资源.平移因子k,r由伸缩因子p,q决定,其数量控制着式(18)中i的取值范围,也就是形函数的个数和矩阵的维度.伸缩因子与平移因子的取值满足

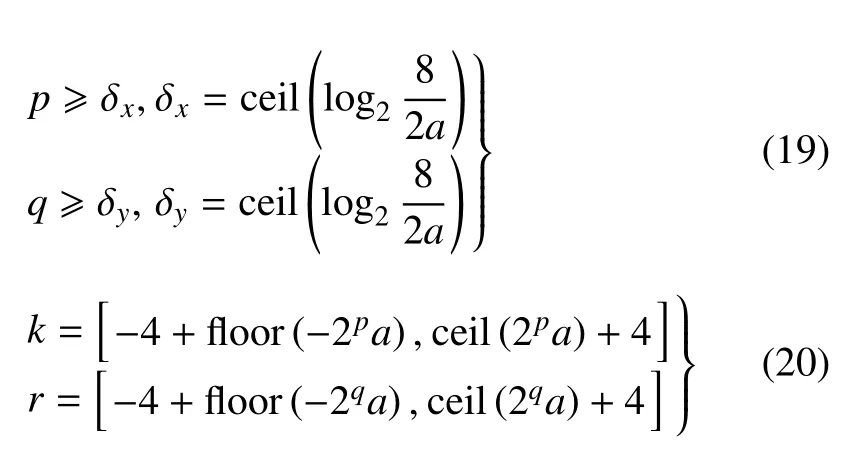
式中,ceil(*)表示最接近并大于*的整数,floor(*)表示最接近并小于*的整数.关于高斯小波函数的详细介绍可以参考文献[45-46].定义一个厚度函数h(x,y)满足

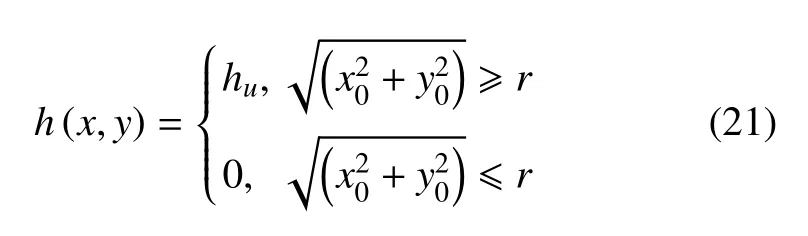
其中,x0和y0分别表示图3 所示开口板坐标系内任意一点的横坐标和纵坐标;hu表示板的标准厚度;r表示圆形开口半径.利用式(21) 中的h(x,y) 替换式(14)、式(15) 中的h,扫描波数求解特征值方程(17)即能得到周期开口板弯曲振动的频散曲线.

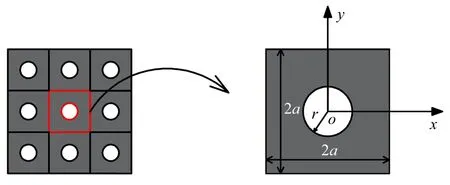
图3 周期开口板分析模型Fig.3 Analysis model of periodic plate with opening

2.2 准确性分析

2.2.1 人工弹簧刚度取值收敛性分析

由前述分析可知,当用人工弹簧模拟周期边界条件时,人工弹簧刚度需要取为无穷,但在实际计算过程中需要用一个较大的值来代替,因此位移约束弹簧和转角约束弹簧刚度的取值在很大程度上影响了计算结果的准确性,需要对人工弹簧刚度取值进行收敛性分析,找到解收敛时的弹簧刚度取值,从而能够准确替代人工弹簧刚度取无穷这一情况.板的长度和宽度都为0.12 m,板的均质厚度取0.001 m,圆形开口半径为0.036 m,选取钢材料为板的材料,密度为7800 kg/m3,弹性模量为210 GPa,泊松比为0.3.从频散曲线中随机选取3 条曲线波数位于kx=ky=π/a处的频率为研究对象,其结果如图4 所示.

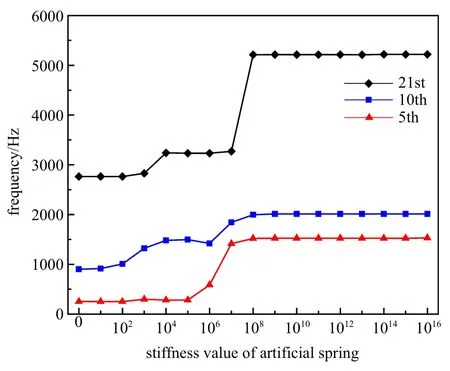
图4 人工弹簧刚度取值收敛性分析Fig.4 Convergence analysis of stiffness of artificial spring

由图4 可以看出,当弹簧刚度系数数值大于1010时,得到的波模态频率值已经趋于稳定,基本不再变化,认为结果已收敛于周期性边界.表明当利用人工弹簧周期性边界条件时,实际计算中只要将刚度系数的数值取为ktx=kty=1010N/m2,krx=kry=1010N/rad 时即可得到收敛的解.

2.2.2 频散特性对比分析

图5 给出了本文方法计算得到的周期开口板弯曲振动频散曲线,为了对比,同时给出了利用文献[41] 中重构位移形函数的方法计算得到的结果.其中两种方法采用的形函数均为高斯函数,板的几何和材料参数一致,伸缩因子、平移因子取值以及扫描波数均保持一致.

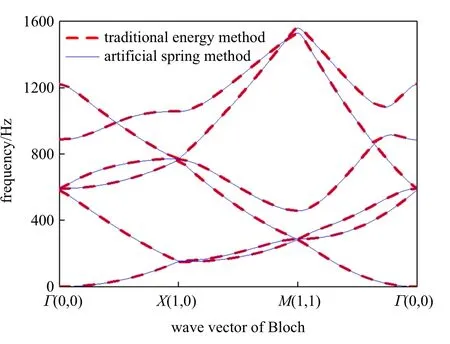
图5 周期开口板弯曲振动频散曲线Fig.5 Dispersion curve of bending vibration of periodic plate with opening

由图5 可以看出,两种方法计算得到的结果基本一致,即0～1500 Hz 范围内,图3 所示的这种周期开口板结构没有产生完全带隙和方向带隙,进一步说明了利用人工弹簧模拟周期边界的准确性.

2.3 效率对比分析

2.3.1 扫描波数的影响

扫描波数决定了频散曲线上点的个数,越大的扫描波数能够得到更为平滑的频散曲线.本节分析了不同扫描波数下,两种方法计算频散曲线的时效性,将对比结果列于表1.分析中保持伸缩因子为6不变.

由表1 可以看出,当扫描波数为30 时,本文方法求解仅需要4.5 s,而传统能量法需要27.5 s,约为本文方法的6.1 倍;随着扫描波数的增大,时间倍数越来越大,本文方法效率性体现得更加明显,当扫描波数为300 时,传统能量法需要268.2 s,约为本文方法的21.8 倍.这是因为传统能量法需要对位移场形函数进行重构以满足周期性边界条件,这就导致结构的动能和应变能矩阵中都含有波数,每扫描一次波数,结构的动能和应变能矩阵都要计算一次,随着扫描波数的增大,动能和应变能矩阵的计算次数也随之增大,这极大地延长了求解时间.而本文提出的利用人工弹簧模拟周期性边界条件的方法,通过将周期性约束条件转变为弹性势能,仅在有边界弹性势能矩阵中包含波数,结构的动能和应变能矩阵只需要计算一次,只有弹性势能矩阵参与扫描波数的循环计算,这就使得求解时间大大缩短.

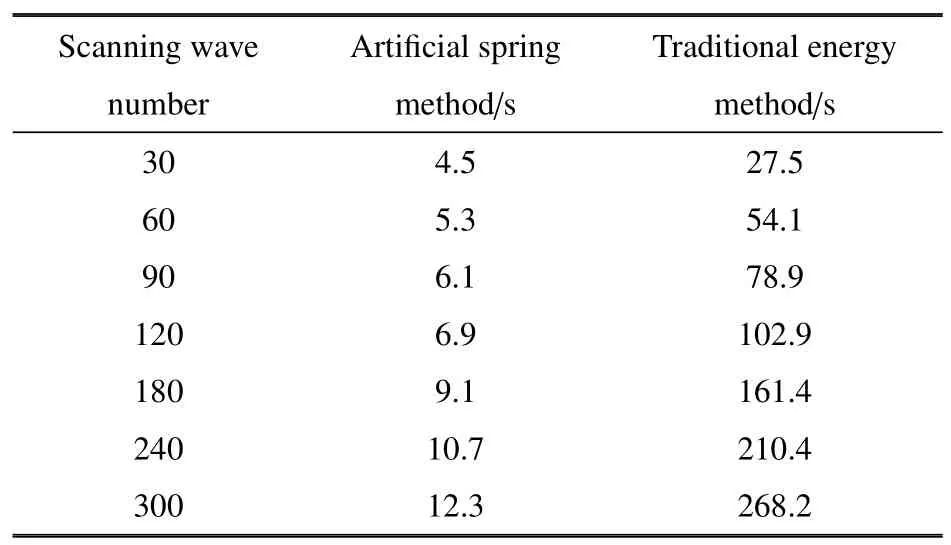
表1 不同扫描波数下计算时效对比Table 1 Comparison of calculation time under different scanning wave number

2.3.2 矩阵维度的影响

前文中提到,伸缩因子控制着解的精度,采用越大的尺度因子使形函数具有更高的分辨率,但同时要求更多的计算资源.平移因子由伸缩因子决定,其数量控制着形函数的个数和矩阵的维度.本节分析了不同伸缩因子(矩阵维度) 条件下,两种方法计算频散曲线的时效性,将对比结果列于表2.分析中保持扫描波数为100 不变.

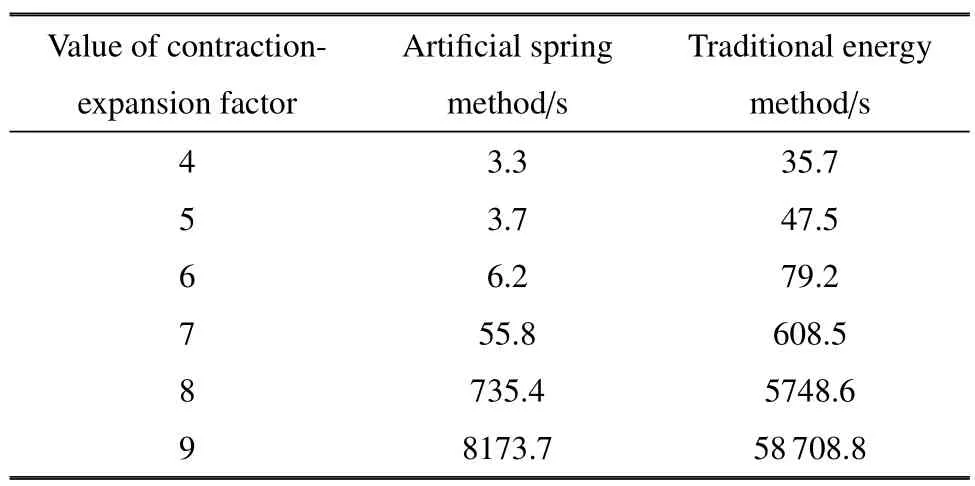
表2 不同矩阵维度下计算时效对比Table 2 Comparison of computational effectiveness under different matrix dimensions

传统能量法需要对位移场形函数进行重构以满足周期性边界条件,这就导致结构的动能和应变能矩阵中都含有波数,结构的动能和应变能矩阵需要随着波数变化进行反复计算,随着伸缩因子取值的增大,平移因子的取值范围也随之增大,动能和应变能矩阵的维度也随之增大,这就导致每次循环计算动能和应变能矩阵的时间增大.

本文提出的利用人工弹簧定义周期性边界的方法,仅在边界弹性势能矩阵中包含波数,结构的动能和应变能矩阵不需要参与波数循环,只需要计算一次,仅有边界弹性势能矩阵参与随波数的循环计算.虽然伸缩因子的增大也导致了边界弹性势能矩阵维度的增大,但其计算量远小于增大结构的动能和应变能矩阵维度的计算量,这就使得随着伸缩因子的增大,本文提出的人工弹簧定义周期边界的方法求解时间增长量远小于传统能量法:由表2 可以看出,当伸缩因子由4 增大到5 时,本文方法求解时间由3.3 s 延长到3.7 s,求解时间延长0.4 s;而传统能量法求解时间由35.7 s 延长到47.5 s,求解时间延长11.8 s,约为本文方法的29.5 倍.同时,在编程计算中,随着矩阵维度的增大,不仅结构的动能和应变能计算时间增大,最后特征值求解的时间也随之增大,因此在表3 中,当伸缩因子由7 增大到8 时,本文方法求解时间从55.8 s 延长到735.4 s,延长了679.6 s.但相比于传统能量法,优势还是很明显,对传统能量法,伸缩因子由7 增大到8 时,求解时间从608.5 s 延长到5748.6 s,延长了5140.1 s.因此,相较于传统能量法,随着模型复杂程度的增加以及分析精度要求的提高,结构的质量刚度矩阵维度以及扫描波数点数随之增大,本文提出的用人工弹簧模拟周期性边界的方法在计算效率上的优势也会越来越明显.

3 周期组合结构振动带隙计算

在铁路工程、土木工程、机械工程等领域,组合结构是一种常见的结构类型.这类结构通常也具有周期性,研究这类组合结构的带隙特性,能够更全面地理解弹性波在结构中的传播特性,从而更好地指导其减振降噪设计.在简化建模过程中,由于组合结构的复杂性,可能是由梁-板耦合、多块板耦合甚至是板-圆柱壳耦合等,这就导致在利用位移形函数进行结构动能和势能的表征时,形成的质量和刚度矩阵维度很大.针对这种大维度矩阵问题,若通过重构满足周期性边界的位移形函数的方法来进行带隙计算,将会面临相当大的计算成本.因此,本节以我国CRSTIII 型无砟轨道结构为例,采用人工弹簧定义周期性边界的方法,计算了周期性组合结构弯曲振动的带隙,并与有限元结果进行了比较.

3.1 模型简化

建立图6 所示的由钢轨、扣件、轨道板和CA 砂浆层组成的无限周期结构.扣件与CA 砂浆层简化为弹簧单元;为同时考虑钢轨和轨道板的弯曲和剪切性质,钢轨简化为Timoshenko 梁单元,轨道板简化为Mindlin 板单元,钢轨选用60 kg/m 钢轨.本文基于钢轨和轨道板的周期性与对称性(假设结构对称及载荷形式对称),可以取一个周期下结构的一半进行建模,模型如图7 所示.l为单个轨道板的长度,相邻轨道板之间是不连续的,s0为轨道板间缝隙的大小.l+s0为钢轨周期,其小周期为l0,且l0=(l+s0)/9.c为轨道板宽度的一半,y*为钢轨距轨道板外侧边缘的宽度.图中分别针对钢轨和轨道板建立了两个笛卡尔坐标系x′O′y′和xOy.

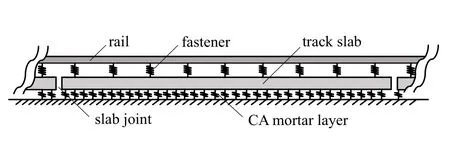
图6 CRTSIII 无砟轨道结构纵断面示意图Fig.6 Schematic diagram of the longitudinal section of the CRTSIII track structure

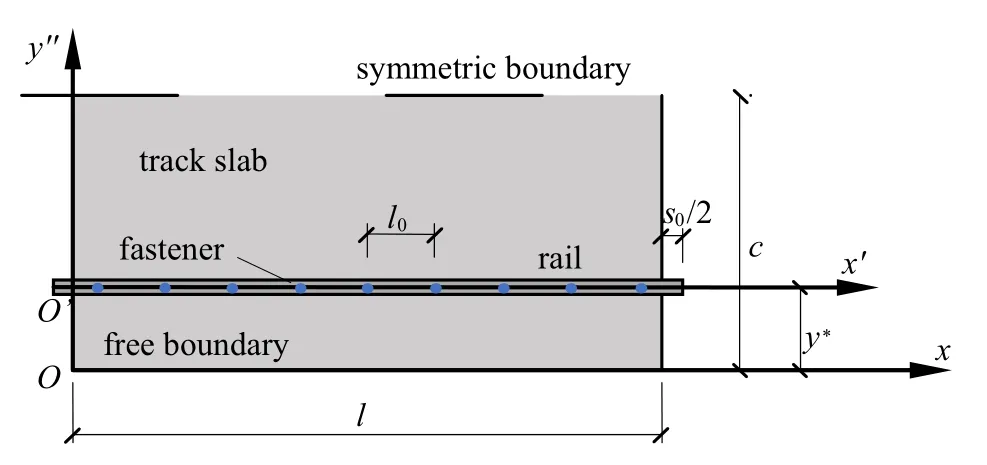
图7 CRTSIII 型无砟轨道结构典型单元示意图Fig.7 Schematic diagram of CRTSIII track structure of a cell

3.2 运动方程的建立

钢轨和轨道板的位移场可以分别写为与式(2)类似的形式,即

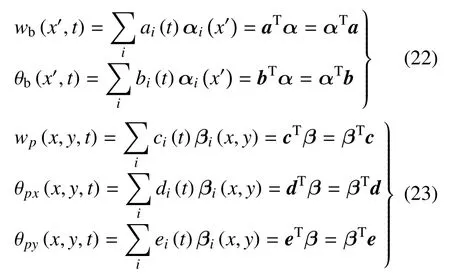
其中,wb(x′,t) 和θb(x′,t) 分别表示钢轨的垂向位移和截面转角函数;wp(x,y,t),θpx(x,y,t),θpy(x,y,t) 分别表示轨道板弯曲振动位移、沿x方向转角以及沿y方向转角函数.钢轨与轨道板位移场形函数都采用第2 节提到的高斯函数.

3.2.1 钢轨的动能和应变能

分析中钢轨考虑为Timoshenko 梁,因此其动能包含了平动动能和转动动能,应变能包含了弯曲应变能和剪切应变能,即

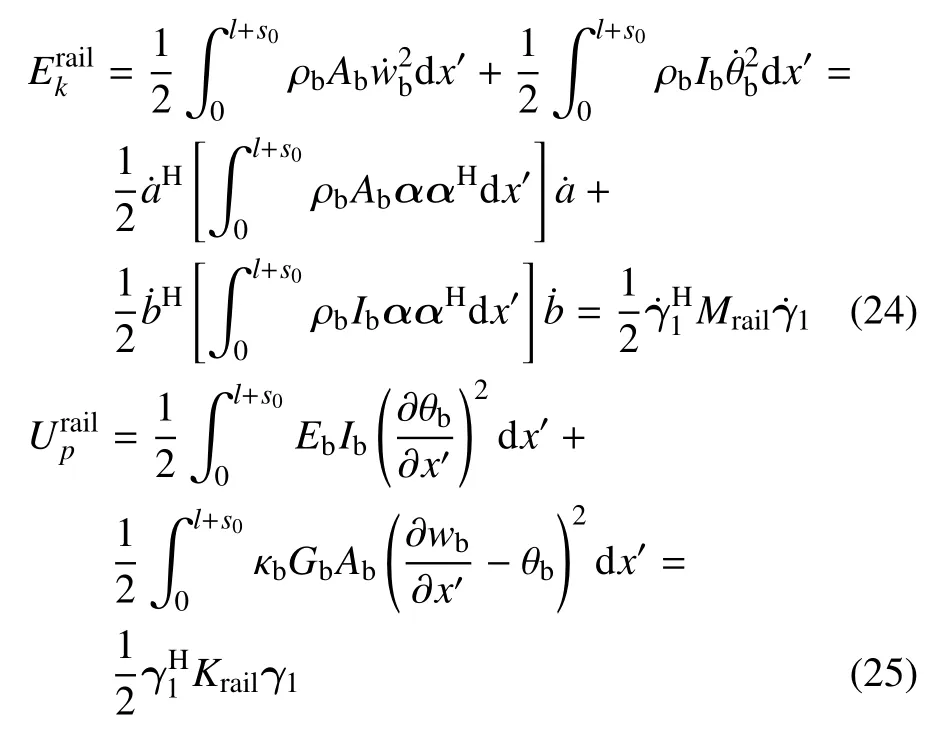
3.2.2 轨道板的动能和应变能

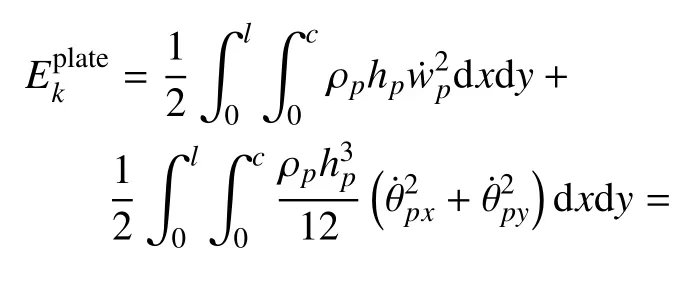
3.2.3 扣件弹性势能与轨道板下弹性地基势能

模型中9 个扣件的总弹性势能可表示为

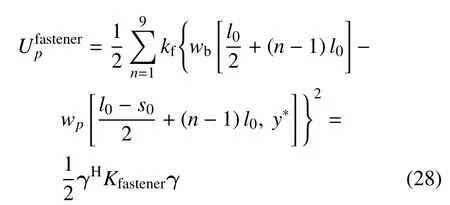
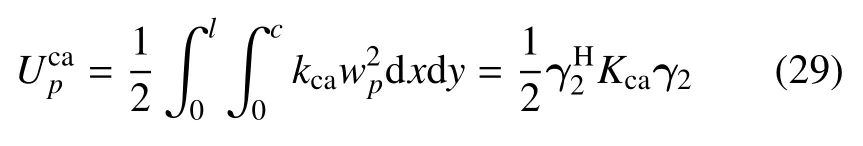
3.2.4 对称边界及周期性边界条件的定义

图7 中xOy坐标系y=c处边界为正对称边界,可认为板边界上转角为0,位移自由,利用人工弹簧模拟正对称边界条件,线弹簧和转角弹簧刚度分别表示为kts和krs,刚度取值参考文献[43].在x′O′y坐标系上x′=0 和x′=l+s0处为Floquet 周期性边界,由于CRSTIII 型轨道板结构是不连续的,相邻轨道板之间存在板缝,因此轨道板没有Floquet 周期性边界.整体结构的边界势能可表示为

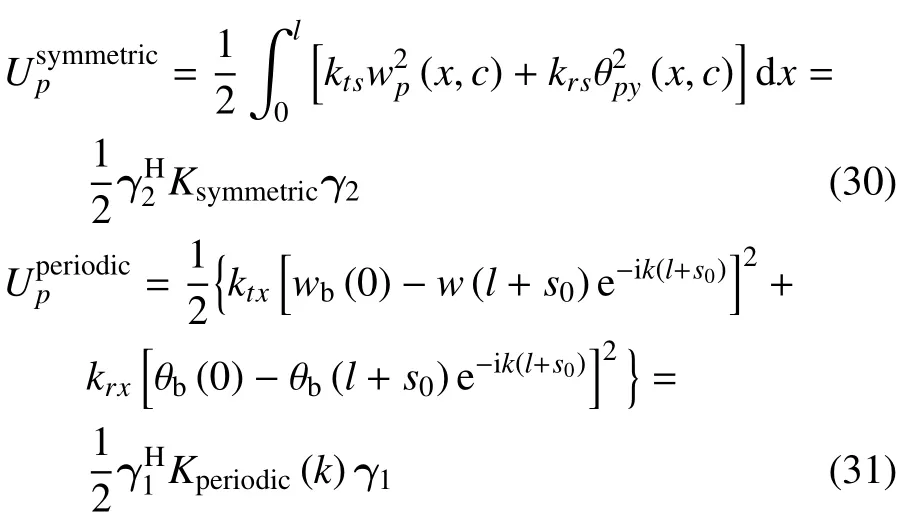
3.2.5 单个周期的拉格朗日能量泛函

单个周期结构的总动能和总势能可表示为

单个周期结构整体的拉格朗日量可写为

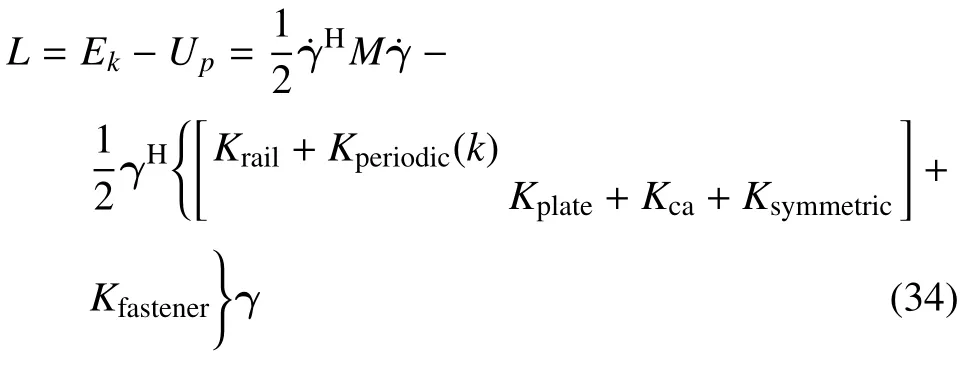
结合前文中提到的欧拉-拉格朗日方程,可以将式(34)转化为标准特征值方程问题,即

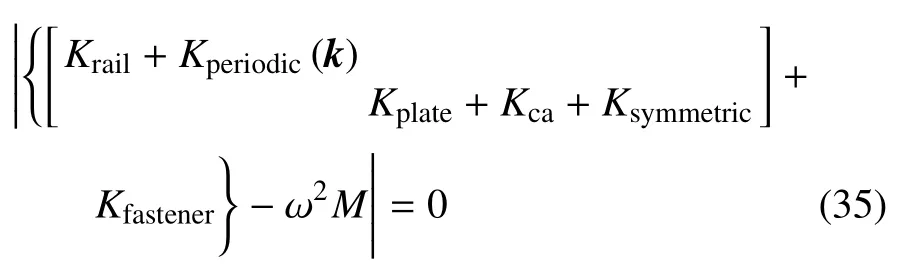
在第一布里渊区扫描波矢k=[-π/(l+s0),π/(l+s0)],求解特征值方程(35)就能得到周期梁-板组合结构弯曲振动的频散曲线.

3.3 算例分析

为了进一步验证本文方法的正确性,建立了单个周期CRSTIII 型无砟轨道结构有限元模型,如图8所示.钢轨与轨道板均考虑为实体单元,扣件与CA砂浆层分别简化为点弹簧和均布弹簧,其中,钢轨与轨道板通过扣件弹簧连接,轨道板与基础通过CA 砂浆均布弹簧连接.轨道板的内边界添加正对称边界条件,在钢轨两端添加Floquet 周期性边界条件,其余边界为自由边界.钢轨、轨道板的几何和材料参数以及扣件刚度、CA 砂浆均布刚度取值与上述半解析模型一致,钢轨密度ρb=7850 kg/m3,截面积Ab=77.45 cm2,截面惯性比Ib=3217 cm4,弹性模量Eb=210 GPa,泊松比νb=0.3;轨道比密度ρp=2300 kg/m3,半宽度C=1.25 m,长度l=5.6 m,厚度h=0.21 m,弹性模量Ep=25 GPa,泊松比νb=0.2;轨道板间缝系S0=0.07 m,轨道与FSB 间距y*=0.492 2 m,垂直连接钢度kf=7.2×107N/m,CA砂浆层的均匀支撑钢度kca=1.723×108N/m3.选用多物理场仿真软件Comsol Multiphysics 中的固体力学模块进行求解,通过设置扫描波数求解得到了周期性无砟轨道结构的振动模态,从中挑选出垂向振动模态进行绘制即能得到垂向振动频散曲线.0～1500 Hz范围内,CRSTIII 型无砟轨道结构垂向振动产生了四阶带隙,图9 给出了两种方法计算结果对比.

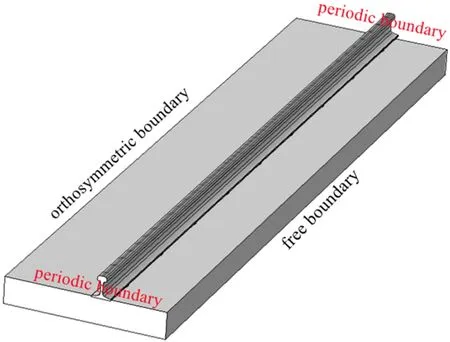
图8 CRTSIII 无砟轨道结构典型单元有限元模型Fig.8 FEM model of typical cell of CRTSIII track structure

图9 CRTSIII 型无砟轨道结构垂向振动频散曲线Fig.9 Vertical vibration dispersion curve of CRTSIII track structure

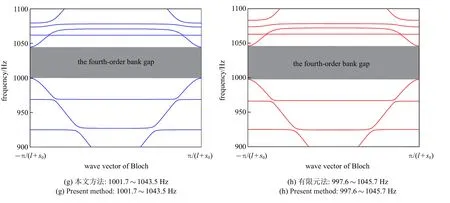
图9 CRTSIII 型无砟轨道结构垂向振动频散曲线(续)Fig.9 Vertical vibration dispersion curve of CRTSIII track structure(continued)

由图9 可以看出,利用人工弹簧定义周期性边界这种方法进行带隙计算与有限元计算结果吻合度很好,再次证明了该方法的准确性.目前,针对此类复杂的周期性组合结构带隙计算问题,主要是通过商业有限元软件来实现.其中仅有Comsol 等少数有限元软件可通过直接设置Floquet 周期性边界并扫描波矢来实现带隙计算.然而由于这类商业软件目前计算模块尚未完善,以Comsol 为例,对于图6 所示的无砟轨道结构(梁-板组合结构)需要采用实体单元建模,计算量较大.利用人工弹簧模拟周期性边界,除周期边界处人工弹簧弹性势能矩阵需随波数变化而重复计算,其他矩阵均只需计算一次,可以解决计算量大的问题.

4 结论

本文基于能量法的基本框架,对传统能量法进行了改进,提出了利用人工弹簧模拟周期性边界条件的方法,实现了周期性边界条件与位移形函数的分离.首先以周期开口板为例,验证了本文方法的准确性,并与传统能量法比较了计算效率;然后,针对周期性组合结构,以我国CRTSIII 型无砟轨道结构为例,分析了其垂向振动带隙特性,并与有限元法进行了比较.通过本文的研究,可得如下结论:

(1)与传统能量法以及有限元法的对比结果表明了本文方法具有很好的准确性.同时,相较于传统能量法,利用人工弹簧模拟周期性边界条件,无需构造满足周期边界的位移形函数,进一步实现了周期边界与位移形函数的分离,成功解决了传统能量法中构造满足周期性边界条件形函数的困难问题,提高了能量法的适用性.

(2)与传统能量法相比,利用人工弹簧模拟周期边界,除周期边界处弹性势能矩阵需随波数变化而重复计算,其他矩阵均只需计算一次,这极大地提高了计算效率,实现了以较低的计算成本对复杂周期结构的带隙进行精确计算.随着模型复杂程度的增加以及分析精度要求的提高,结构质量、刚度矩阵的维度以及扫描波数点数也随之增多,本文方法在计算效率上的优势会更加明显.