于要杰 刘 锋 高 超 冯 毅,2)

*(西北工业大学航空学院,西安 710072)

†(加州大学尔湾分校机械与航天工程系,美国加利福尼亚州 92697-3975)

**(成都流体动力创新中心,成都 610071)

引言

高阶精度数值格式因其高分辨率、低色散和低耗散等特点正日益受到关注[1-2].相比目前工业界最常用的二阶精度格式,高阶精度格式被认为在花费相同计算代价的前提下具备获得更高精度数值结果的巨大潜力.当前最常见的高阶精度数值格式主要包括基于结构网格的高阶有限差分方法[3-4]、非结构网格上的有限体积法[5-6]以及基于局部单元近似的间断有限元(discontinuous Galerkin,DG)[7-8]、谱体积(spectral volume,SV)[9]和谱差分(spectral difference,SD)[10]等方法.

最近,一种基于非结构网格的高阶精度通量重构格式(flux reconstruction,FR)因其构造简单且更加通用而愈加流行.FR 格式最先于2007 年由Huynh[11-12]提出并证明了,至少对于一维线性方程,FR 格式通过不同修正多项式的选择,不仅囊括了DG 和SD 这两种格式,并且能够产生新的高阶格式.2009 年,Wang和Gao 等[13]提出“lifting collocation penalty,LCP”格式并将其推广到欧拉方程和Navier-Stokes 方程.由于FR 和LCP 这两种格式具有高度的相似性和内在联系,因此后来也被Huynh 和王志坚[14]联合命名为FR/CPR (correction procedure via reconstruction) 格式.2011 年,Vincent 等[15]提出了一种针对一维线性对流方程的能量稳定的FR 格式,即VCJH 格式,后续又在此格式的基础上开发了三维并行CFD 求解器Hi-FiLES[16]和PyFR[17].如今,FR 已不仅是一种高阶格式,它还为几种现有的高阶格式,例如SD 和DG,提供了一个统一的框架.相比DG 和SD 的原有形式,FR 在概念上更加简单且计算效率更高[18].关于FR和DG 间的联系,Allaneau 和Jameson[19]和De Grazia等[20]已经进行了深入研究.

尽管FR 格式已经取得了较大的进步,但将其应用于复杂外形流动的数值模拟时,仍然有一些难点问题需要解决,例如计算效率的问题、曲面边界处理方法、间断侦测方法与限制器的构造等.其中,计算效率的问题在很大程度上制约了FR 格式在实际工程中的应用.在当前的FR 格式应用中,时间离散多采用存储需求小且易实现的显式Runge-Kutta 类方法[21].但随着格式精度的提高,FR 对应的CFL 稳定性条件越来越严格,时间推进步长会受到明显的限制.对一些复杂流动问题(流场中存在边界层、剪切层等小尺度流动结构)的计算更是如此.因此,发展FR 格式的加速收敛方法,具有十分重要的工程应用价值.目前常用的加速收敛方法在算法层面主要有隐式时间推进方法、当地时间步长、残差光顺、多重网格以及物理层面的并行计算技术等.在这些方法中,隐式时间推进方法的加速效果是十分明显的[22].相比显式时间方法,隐式方法受CFL 稳定性条件的约束小,可以选取更大的时间推进步长,进而能够有效地提高CFD 求解的效率.近年来已有学者提出了多种基于FR 格式的隐式时间方法,例如LU-SGS 方法[23]、预处理GMERS 方法[24]、无矩阵(Jacobianfree) Newton Krylov 方法[25]以及多色高斯-赛德尔(multi-colored Gauss Seidel,MCGS) 方法[26]等.这些文章中以数值实验证明,使用隐式方法的FR 格式相比显式具有非常明显的计算效率提升.以上这些隐式时间方法大都是在CPU 架构上实现,由于基于局部单元近似的FR 格式的绝大多数操作都是在局部单元中进行,计算量较为集中,因此更适合GPU 计算.当前,基于CPU 并行策略的有限体积求解器一般只能使用并行集群性能峰值的5%～10%,而使用GPU 计算的FR 格式计算速度最高可以达到性能峰值的58%左右[27].因此,基于GPU 并行的隐式时间推进方法有望进一步提高FR 格式的计算效率.

近年来,GPU 计算在CFD 领域中的应用已经越来越普遍.已有的研究结果表明[27-29],对于相同规模的问题,GPU 并行能够较大程度地提升高阶CFD 程序的计算效率.例如,Romero 等[30]利用显式时间方法的VCJH 格式计算非定常流动问题,发现GPU 并行相比基于MPI 并行的CPU 节点具有更高的计算效率.Vermeire 等[31]使用PyFR 求解器在多个GPU 卡上以三维Taylor-Green 涡和SD7003 翼型为例进行隐式大涡模拟计算,发现与使用CPU 节点并行的商业CFD 软件Star-CCM+相比,在计算成本相当的前提下,5 阶FR 计算得到的模拟结果更精细.最近,Jourdan 和Wang 等[32]在美国“Summit”超级计算机上使用FR/CPR 高阶求解器,分别利用了800 个节点的CPU 和4800 个GPU 卡进行了大涡模拟计算,发现使用显式时间推进方法时,在六面体和四面体这两种网格单元类型上,GPU 相比CPU 并行分别有一个和两个量级左右的加速效果.

在上述的大规模CFD 数值模拟中,基于FR 格式的GPU 计算使用的都为显式时间方法.为了探索如何进一步提高FR 格式的求解效率,本文以二维欧拉方程为例,提出一种基于高阶FR 格式的单GPU并行隐式时间求解方法.通过块Jacobi 迭代的方式,改变了经过隐式离散后全局线性方程组左端矩阵的特征,克服了影响求解并行性的相邻单元依赖.最终,将解全局线性方程组转化解一系列局部单元线性方程组,进而又通过LU 分解法并行求解这些局部线性方程组.数值实验表明,相比显式方法而言,该隐式方法在计算效率方面至少有一个量级的提升.并且,该隐式方法不局限于FR 格式,对DG 和SD 等基于局部单元近似的高阶格式也具有参考意义.

1 控制方程

无黏流动的控制方程为欧拉方程,其二维形式如下

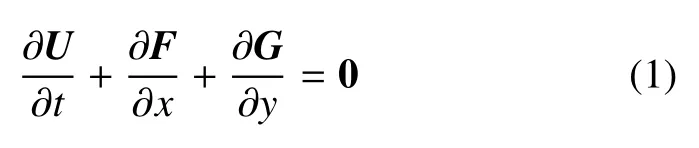
其中,U=[ρ,ρu,ρv,ρE]为守恒变量,F和G分别为x和y方向的无黏通量

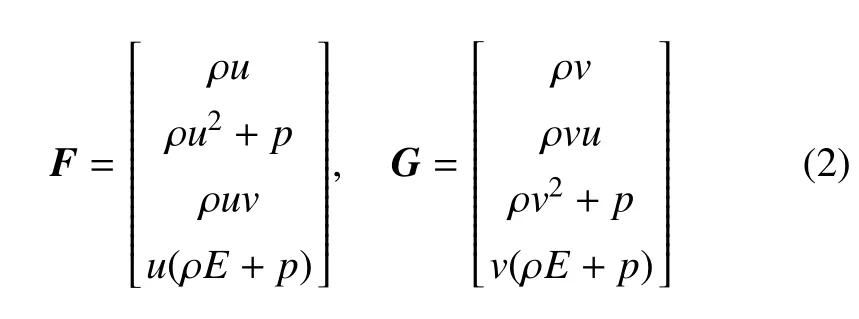
式中,ρ 是密度,u和v分别表示x和y方向的速度,p为压强,E代表单位质量流体的总能量。本文中假设流体为理想气体,则有

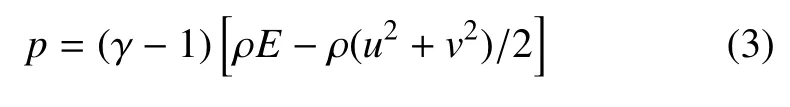
其中,γ=Cp/Cv为比热容比,本文中其值为1.4.

2 高阶通量重构格式

本节将以二维标量守恒律为例来简要地介绍FR格式的基本思想.在区域Ω ∈R2上的一般形式的二维标量守恒律形式为

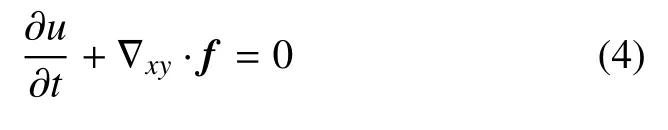
其中,u=u(x,y,t)为标量守恒量,f=(f,g)为通量项,f=f(u)和g=g(u)分别为f在x和y方向的分量.

下面将区域Ω 分割为N个互不重叠的四边形子区域且子区域满足如下条件

为了数学书写的方便以及计算效率方面考虑,首先通过如图1 所示的变换将物理域(x,y)上任意Ωn转换到计算域(ξ,η)上的一个标准单元ΩS(为了叙述简洁,下面将省略下标n).

图1 将任意四边形单元变换到一个标准单元Fig.1 Mapping of an arbitrary physical space quadrilateral element to the standard reference quadrilateral element

经过以上变换后,子区域Ωn上的方程(4) 变换为

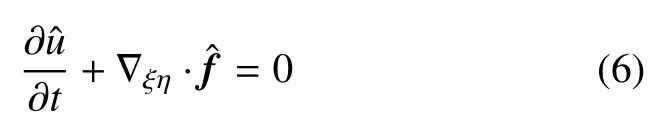
其中,顶标“ˆ”代表其为计算域(ξ,η)上的变量,计算域(ξ,η)和物理域(x,y)上的变量存在如下关系

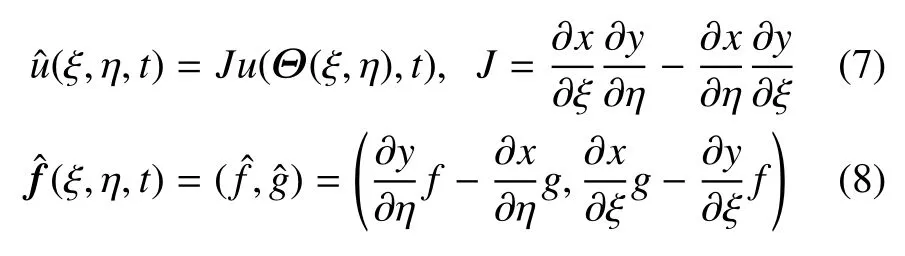
其中,右上标“δ”代表近似解,“D”表示是单元上的局部解,是求解点(ξi,ηj)处的近似解,li和lj是相对应的拉格朗日插值多项式.在单元内部是连续的,但在相邻单元之间是间断的.图2 中给出了p=2 时在四边形单元上求解点和后续用于通量修正的边界面通量点的分布.

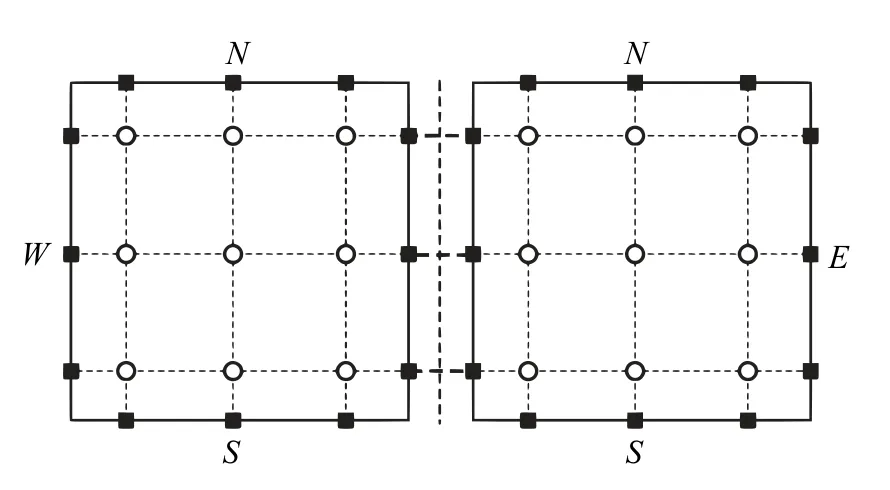
图2 两个四边形单元上求解点(圆圈)和通量点(方块)的分布(p=2)Fig.2 Arrangement of solution points(circles)and flux points(squares)on a pair of quadrilateral elements(p=2)

在计算散度项之前,首先进行通量项的构造和计算.参照方程(9) 中近似解的构造,同样可以获取局部通量.但由于仅在单元内部连续,而在单元之间并不连续.为了满足格式守恒性的要求,FR 通过增加修正项的方式构造在单元界面处连续的通量.因此,连续的全局通量由单元内的局部通量和修正通量构成上式中,局部通量通过p阶的插值多项式进行近似

综上,经过FR 格式空间离散之后的半离散方程为

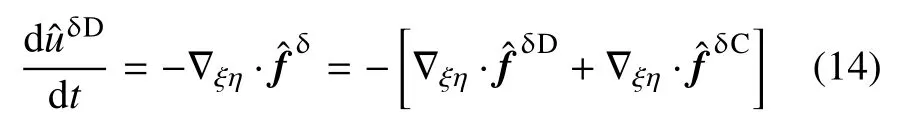
上述常微分方程组可进一步通过显式或隐式的时间推进方法进行求解.

3 隐式时间推进方法

二维欧拉方程经过空间离散之后得到的半离散方程可进一步写作如下形式

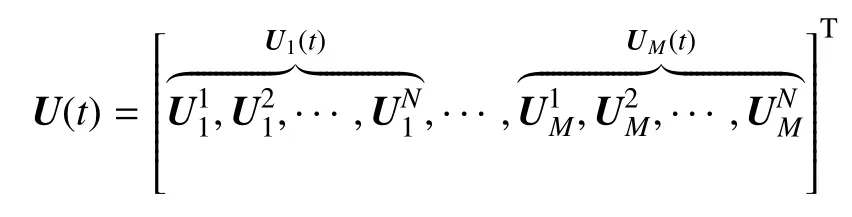
在上式中为M×N×4 维度的全局解向量,其中,M和N分别代表网格单元总数以及每个单元内求解点的个数,UM(t)为第M个单元上的局部解,是第M个单元第N个求解点上包含守恒变量的解向量.

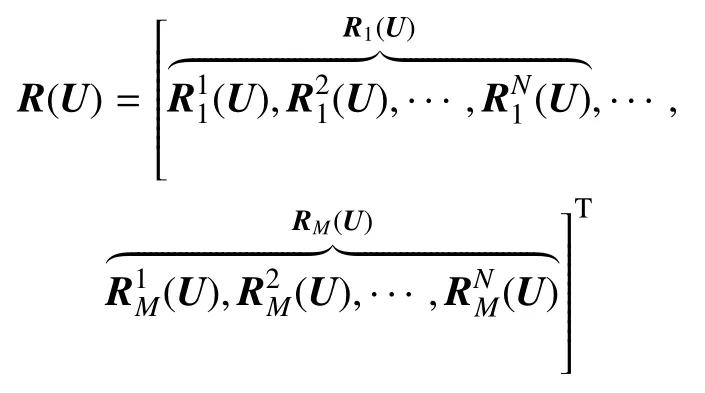
代表右端残差项,RM(U)是第M个单元上的局部残差,为第M个单元第N点上残差.

由于本文计算的是定常流动,无需考虑时间精度,因此时间项的离散使用一阶向后隐式差分格式.方程(15)经过该方法离散后可得

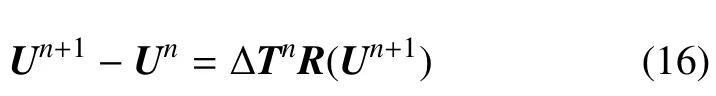
式中,Un=U(tn)和Un+1=U(tn+1)分别为tn和tn+1时刻的解.ΔTn为一个包括时间步长的对角矩阵,其与Un具有相同的维数,其具体形式为

由于方程(16)中的R(Un+1)是非线性的,通过泰勒展开对其线性化,则有

上式中,∂R/∂U|Un为全局雅可比矩阵.将方程(18)代入方程(16)并整理得

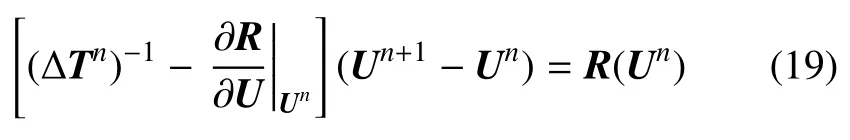
上式中,tn+1时的解Un+1需要先求解线性方程组才能获取.

3.1 块雅可比迭代

线性方程组的求解可分为直接法和迭代法.当网格规模较大时,使用直接法求解效率低下且内存占用较大.因此本文通过迭代法求解方程(19),所用的迭代方法为雅可比迭代.

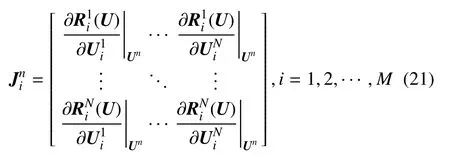
首先对方程(19) 左端的矩阵进行分解.令A=[(ΔTn)-1-∂R/∂U|Un].则A=D-N可看作是由分块对角矩阵D和剩余非对角部分N组成.其中,分块对角矩阵D为

与此同时,N的矩阵形式是

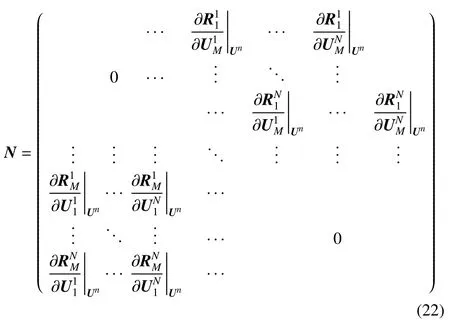
式中的N为一稀疏矩阵.经过上述分解之后,对全局线性方程组(19)进行迭代求解,可得

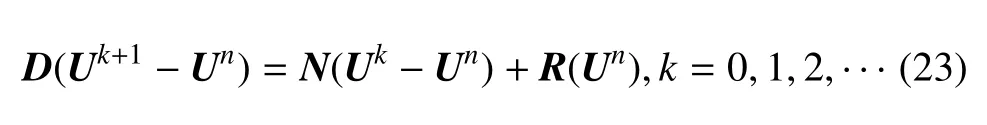
在上式中,k为雅可比迭代指标.当k→∞时,雅可比迭代解Uk+1趋近于下一个时刻的解Un+1.对于定常问题的计算,k只需要设置为有限的值,当n→∞,Uk+1和Un最终都将趋向于所求的定常解.

为了避免非对角部分N的计算.对方程(23)两侧同时减去D(Uk-Un),则有

上式经进一步整理后可得

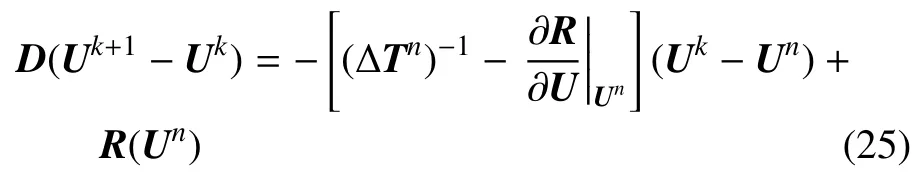
和方程(18)类似,将R(Uk)在R(Un)处进行泰勒展开

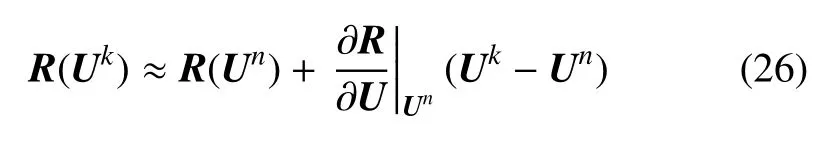
上式可进一步写成

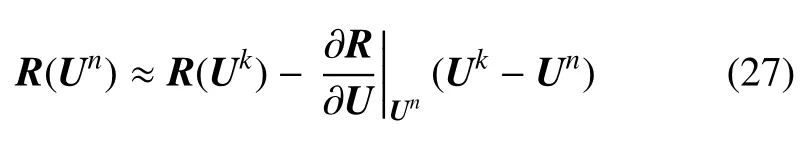
将方程(27)代入到方程(25)中消去全局矩阵相关的一项∂R/∂U|Un(Uk-Un),并最终整理可得

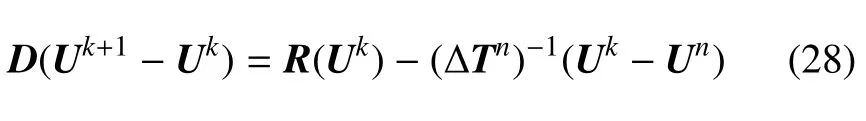
式中,D=diag{D1,D2,···,DM}.

方程(28)和方程(19)相比,它的左端矩阵D是一个分块对角矩阵,这使得求解全局线性方程组(19)的问题解耦为求解一系列局部单元上的小型线性方程组.

值得注意的是,全局矩阵A的分解方式并不唯一,如将其分解为分块上三角矩阵U和分块下三角矩阵L,即为Gauss-Seidel 迭代法.此时需要求解的方程的左端矩阵为分块下三角矩阵L.由于此时Uk+1存在数据依赖问题,无法同时更新,为了并行地求解该方程,需要使用图着色技术,所得方法即为更复杂的MCGS 法[26].

3.2 局部线性方程组的求解

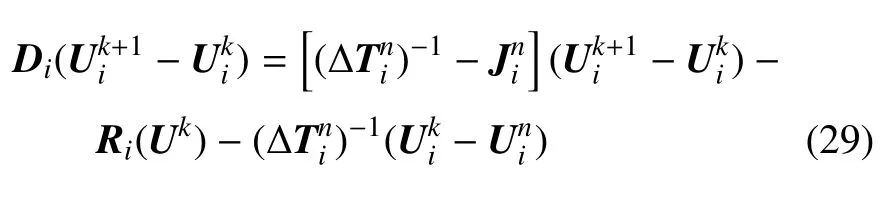
方程(28)可进一步写成一系列局部单元线性方程组.对于第i(1 ≤i≤M)个单元,则有上式中,i为单元指标,n是时间迭代指标,k为雅可比迭代指标.为第i个单元对应的单元雅可比矩阵,在下一小节中将讨论其具体计算方法.以上获取的M个局部线性方程组(29),其左端矩阵规模较小,在程序中通过调用cuBLAS 函数库使用LU 分解法实现同步求解.

3.3 单元雅可比矩阵的计算

本文中所用是解析法与自动微分相结合的方法.由式(13)可知,第i个单元上,FR 格式离散后的残差Ri是不连续通量的散度和修正通量的散度之和.则单元雅可比矩阵为

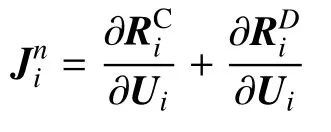
4 数值实验

本节中以二维Bump 流动和NACA0012 翼型无黏绕流两个算例来展示隐式方法的精度和效率.为了进行计算效率的对比研究,所有算例均同时使用显式和隐式两类方法进行.显式方法为具有TVD 性质的三级Runge-Kutta(TVD RK3)方法[21],同时使用局部时间步长和多重网格(pmulti-grid)方法加速其收敛.隐式方法为本文中所提出的块雅可比迭代的方法.隐式方法的时间步长ΔTn由CFL 数决定,CFL数初始值为2,并随迭代步数指数增长,最大值为104.

所有算例均使用高阶并行通量重构软件HAFR(heterogeneous architecture flux reconstruction) 在型号为英伟达GeForce RTX 2080ti 的单个GPU 卡上计算.为了保证FR 方法在边界的精度不至于下降,算例中用到的网格是由开源网格生成软件Gmsh 生成的二阶曲边网格.计算的收敛性通过密度残差的L2范数判断,当其下降到10-14以下或平稳而不再下降时便认为计算已稳态收敛并终止.

4.1 无黏亚声速Bump 算例

本算例是 international workshop on high-order CFD methods[39]给定的一个二维无黏验证算例.该问题的物理域为[-1.5,1.5]×[0,0.8],底边的几何描述为y=0.062 5e-25x2.左侧为亚声速入口边界条件(给定入口总压和总温),右侧出口为出口边界条件(给定静压),上下边界均为滑移壁面边界条件.来流的马赫数Ma=0.5 且攻角为零度.尽管该流动的精确解未知,但由于流动为亚声速无黏流动且流场光滑,因此可通过熵来衡量解的精度,流场中熵的计算公式如下

式中的积分在HAFR 程序中通过10 阶高斯积分法进行计算.

计算中所使用的网格由粗到细(即h-refinement)为：R1(12×4),R2(24×8),R3(48×16)和R4(96×32),图3 是R2 网格的示例.对于同一网格,同时还将使用p=2,3,4 阶的插值多项式(即p-refinement)进行计算.

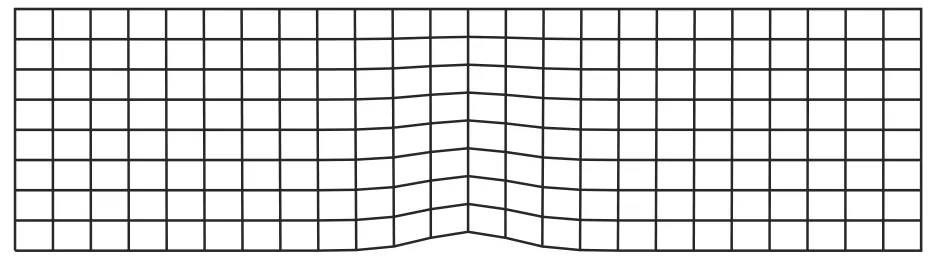
图3 本算例中所用的24×8 的四边形网格Fig.3 Quadrangular mesh(24×8)used in the case

首先从数值精度的角度分析计算结果.表1 为HAFR 程序使用块雅可比迭代隐式方法在四组网格上,插值多项式为p=2,3,4 阶时的熵以及数值精度.从表中可知,对任意一阶插值多项式阶数而言,网格加密的过程中熵也随之降低.同时,给定某组网格,提高插值多项式的阶数也同样会导致熵的降低.正如图4 所示,在R2 网格上使用p=3 和p=4 阶插值多项式得到的下壁面马赫数等值线相比p=2 的更为光滑.此外还观察到,对于p=2,3,4 阶插值多项式,在4 组网格上获取的数值精度,都近似达到p+1阶这一理论值,这也验证了HAFR 的计算精度.

图4 在24×8 的网格上使用p=2,3,4 阶插值多项式计算所得的马赫数云图Fig.4 Mach number contours calculated on the 24×8 mesh with p=2,3,4 polynomial orders

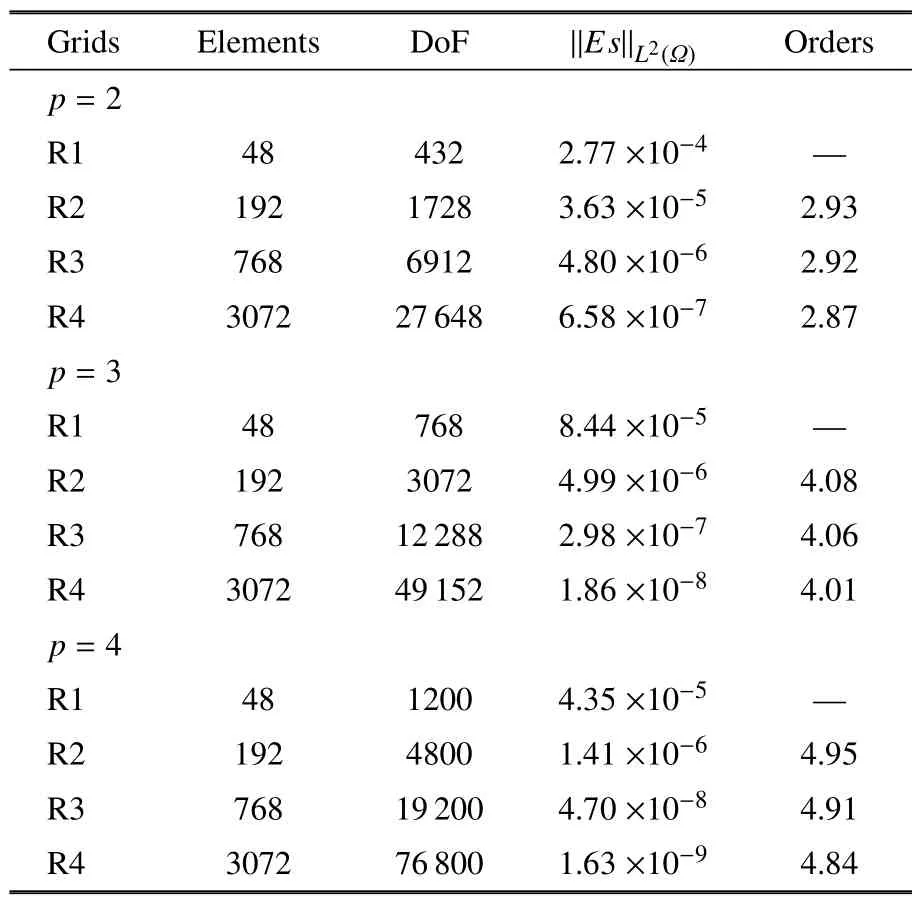
表1 在四组网格上,使用p=2,3,4 阶多项式时的熵和数值精度Table 1 Entropies and numerical orders on four different grids with p=2,3,4 polynomial orders

下面从计算效率的角度进行分析.图5 是HAFR程序使用显式和隐式两种方法在4 组网格上、插值多项式为p=2,3,4 阶时密度残差随迭代次数的收敛情况.

在图5 中,左右两列子图分别为使用块雅可比迭代隐式和TVD RK3 显式时间方法的计算结果.从迭代次数来看,对同一阶插值多项式,显式方法和隐式方法收敛所需的迭代次数都随着网格的加密而增大.对于同一网格,使用更高阶的插值多项式都会导致迭代次数的增多.但同时发现,隐式方法的迭代次数随自由度(degree of freedom,DoF)增幅较小,并且对于同一网格或同一阶插值多项式,隐式方法所需的迭代次数要远远小于显式方法.例如,在R1 网格上,隐式方法收敛的的迭代次数均在80 步以内,而显式方法最快也需要1000 步左右才能收敛.

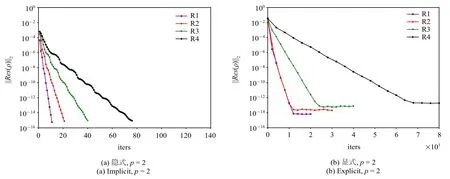
图5 在四组网格上,插值多项式为p=2,3,4 阶时,使用隐式和显式方法所得到的密度残差||Res(ρ)||2 随迭代次数的变化Fig.5 Density residual||Res(ρ)||2 versus the iteration numbers for the explicit and implicit time-marching schemes on four different grids with p=2,3,4 polynomial orders

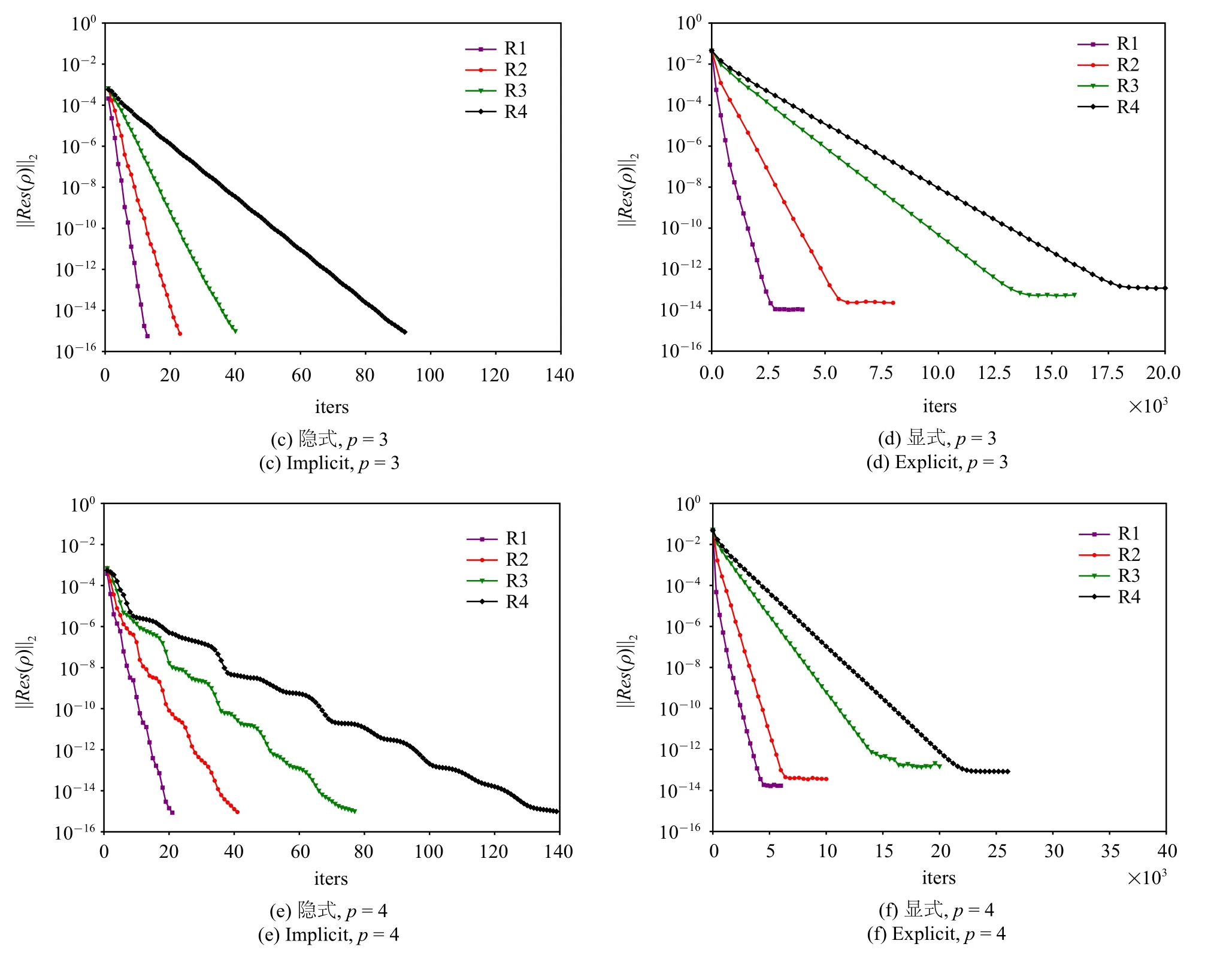
图5 在四组网格上,插值多项式为p=2,3,4 阶时,使用隐式和显式方法所得到的密度残差||Res(ρ)||2 随迭代次数的变化(续)Fig.5 Density residual||Res(ρ)||2 versus the iteration numbers for the explicit and implicit time-marching schemes on four different grids with p=2,3,4 polynomial orders(continued)

在密度残差收敛方面,使用隐式方法的计算的密度残差均能收敛到10-14这一量级.但显式方法的收敛性随着自由度的增大变差,其值下降到某个量级后将无法下降,例如使用p=2 阶插值多项式时,在R1 网格上的密度残差能够收敛10-14量级,但在R4 网格上仅能下降到10-13这一量级.

在GPU 计算时间方面,表2 为HAFR 程序采用块雅可比迭代隐式方法在4 组网格上,使用p=2,3,4 阶插值多项式计算收敛所用的迭代次数和GPU 墙钟时间.从表2 可知,隐式方法计算收敛所用时间随着自由度的增大而增大.

表2 在四组网格上,插值多项式为p=2,3,4 阶时,使用隐式时间方法时的迭代次数和墙钟时间Table 2 Iteration numbers and wall-clock times for the implicit time-marching scheme on four different grids with p=2,3,4 polynomial orders

图6 是HAFR 程序分别使用块雅可比隐式和TVD RK3 显式时间方法,在不同网格上,使用p=2,3,4 阶插值多项式时所用的墙钟时间对比.从图6中可看到,对每一组计算,隐式方法收敛所用的时间明显小于显式方法.在所有算例中,隐式方法相比显式至少有一个量级的加速效果.

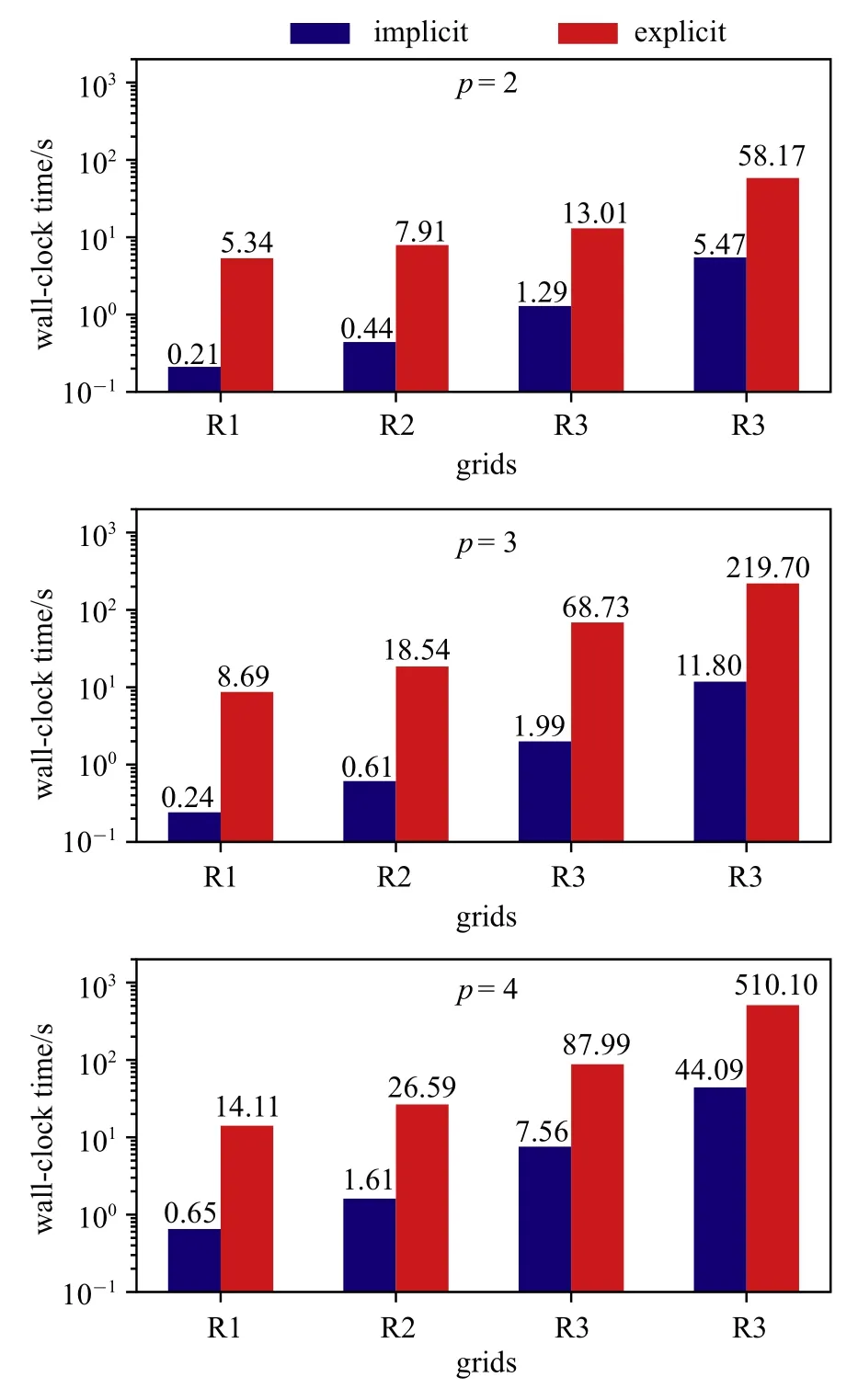
图6 在四组网格上,插值多项式为p=2,3,4 阶时,使用隐式和显式方法所用的计算时间Fig.6 Wall-clock times for the explicit and implicit time-marching schemes on four different grids with p=2,3,4 polynomial orders

4.2 NACA0012 翼型无黏绕流

在上一个Bump 算例中所使用的网格较为均匀,为了进一步考察在非均匀网格条件下块雅可比迭代隐式方法的计算效率,下面对NACA0012 翼型无黏绕流进行数值模拟.在此算例中,自由来流的马赫数为0.5 且攻角为零度.NACA0012 翼型表面为滑移壁面条件,远场为特征边界条件,远场与翼型的距离大约为100 个弦长.

计算中用到的网格为Gmsh 生成的O 型网格,网格分为3 组：R1(32×32),R2(44×64)和R3(128×128).图7 为R1(32×32) 网格的示意图.对于同一网格,还将分别使用p=2,3,4 阶的插值多项式(即prefinement)进行计算.

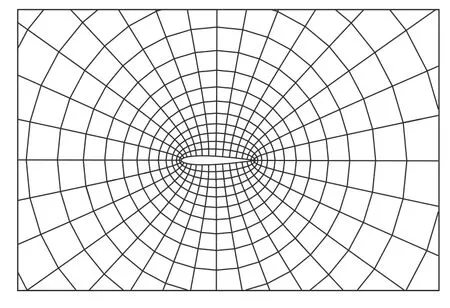
图7 本算例中所用的32×32 的O 型四边形网格Fig.7 O-type quadrangular mesh(32×32)used in this case

下面对 NACA0012 数值模拟结果进行分析.表3 为HAFR 程序采用块雅可比迭代隐式方法在三组网格上,使用p=2,3,4 阶插值多项式计算收敛所用的迭代次数和GPU 墙钟时间.和上个算例中类似,可观察到无论是网格加密还是提高插值多项式阶数,这两种增大自由度的方式都会导致迭代次数和GPU计算时间的增多.

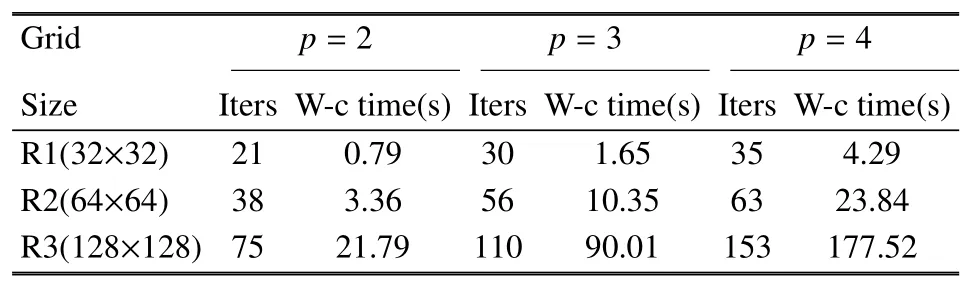
表3 在三组网格上,插值多项式为p=2,3,4 阶时,使用隐式时间方法时的迭代次数和墙钟时间Table 3 Iteration numbers and wall-clock times for the implicit time-marching schemes on three different grids with p=2,3,4 polynomial orders

图8 是HAFR 程序分别使用隐式和显式时间方法,在不同网格上,使用插值多项式为p=2,3,4 时所用的墙钟时间对比.从图8 中可知,对于每一组计算,使用块雅可比迭代隐式方法收敛所用的时间相比TVD RK3 显式方法至少有一个量级的加速效果.

图8 在三组网格上,插值多项式为p=2,3,4 阶时,使用隐式和显式方法所用的墙钟时间Fig.8 Wall-clock times for the explicit and implicit time-marching schemes on three different grids with p=2,3,4 polynomial orders

图9 为HAFR 程序使用显式和隐式两种方法在三组网格上、插值多项式为p=2,3,4 阶时密度残差随迭代次数的收敛情况.在图9 中,左右两列子图分别为使用块雅可比迭代隐式和TVD RK3 显式时间方法的结果.从迭代次数来看,对同一阶插值多项式,显式方法和隐式方法收敛所需的迭代次数都随着网格的加密而增大.对于同一网格,使用更高阶的插值多项式会导致迭代次数的增多.但同时,相比显式方法,隐式方法的迭代次数随自由度增幅较小,并且对于同一网格或同一阶插值多项式,隐式方法所需的迭代次数要远远小于显式方法.

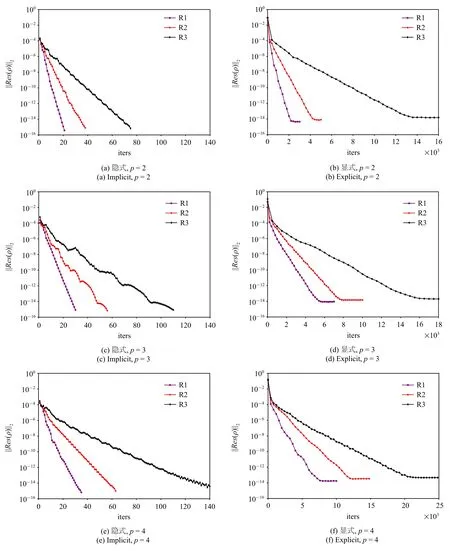
图9 在三组网格上,插值多项式为p=2,3,4 阶时,使用隐式和显式方法所得到的密度残差||Res(ρ)||2 随迭代次数的变化Fig.9 Density residual||Res(ρ)||2 versus the iteration numbers for the explicit and implicit time-marching schemes on three different grids with p=2,3,4 polynomial orders

在密度残差收敛方面,在3 组网格计算中,使用块雅可比迭代隐式方法计算的密度残差均能收敛到10-14这一量级.但TVD RK3 显式时间方法的收敛性随着自由度的增大变差,其值下降到某个量级后将无法下降.因此从残差收敛角度,基于块雅可比迭代的隐式方法要优于TVD RK3 显式方法.

综上,随着自由度的增大,显式和隐式方法收敛所需的迭代次数都会增多.但对于同一网格或同一阶插值多项式,隐式方法所需的迭代次数和计算时间要明显小于显式方法,且隐式方法的残差下降幅度要比显式方法更大.

5 结论

为了提高FR 方法的求解效率,本文提出一种基于雅可比块迭代的高阶FR 格式求解定常二维欧拉方程的单GPU 隐式时间推进方法.通过雅可比块迭代的方式,克服了影响求解并行性的相邻单元依赖,使得只需存储和计算对角块矩阵.最终将求解全局线性方程组转化为求解一系列局部单元线性方程组.这些局部的线性方程组在GPU 上又可利用LU 分解法并行求解.

文中通过二维无黏Bump 流动和NACA0012 无黏绕流两个算例表明:随着自由度的增大,块雅可比迭代隐式方法收敛所需的迭代次数和计算时间都会增多.但对于同一网格或同一阶插值多项式,该隐式方法所需的迭代次数要明显小于TVD RK3 显式方法,且此隐式方法的残差下降幅度要比TVD RK3 显式方法更大.在计算时间方面,对于文中的每一组计算,雅可比块迭代隐式方法收敛所用的GPU 计算时间明显小于TVD RK3 显式方法,且计算效率至少有一个量级的提高.

附录

二维欧拉方程的雅克比矩阵为