LI Dan and LI Zhongping

College of Mathematic and Information,China West Normal University,Nanchong 637009,China.

Abstract. In this paper,we study the asymptotic behavior of solutions to a quasilinear fully parabolic chemotaxis system with indirect signal production and logistic sourceunder homogeneous Neumann boundary conditions in a smooth bounded domainΩ ⊂Rn (n ≥1),where b ≥0, γ ≥1, ai ≥1, µ,bi>0 (i=1,2), D,S ∈C2([0,∞))fulfilling D(s)≥a0(s+1)−α,0 ≤S(s)≤b0(s+1)β for all s ≥0,where a0,b0>0 and α,β ∈R are constants.The purpose of this paper is to prove that if b ≥0 and µ>0 sufficiently large,the globally bounded solution(u,v,w)with nonnegative initial data(u0,v0,w0)satisfies

Key Words:Chemotaxis system;indirect signal;logistic source;asymptotic behavior.

1 Introduction

In 1970,Keller and Segel proposed a classical biological chemotaxis model[1]

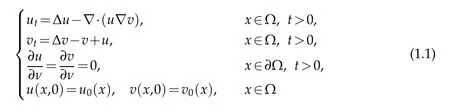
withurepresents the density of cells,vis the density of a chemical signal.In the first equation of(1.1),∆udenotes self diffusion and the cross-diffusion term −∇·(u∇v)means that the cell is moving towards a high chemical concentration.In the second equation of(1.1),∆vis the self-diffusion of the chemical signal,−v+udenotes the consumption ofvand direct production by the cellu.The system(1.1)describes the chemotactic behavior of cells in numerous biological processes[2,3],and the biological model(1.1)plays a key role.Whenn=1,the system(1.1)has a unique global solution[4].Whenn=2,there is a critical mass phenomenon[5],if,the system(1.1)processes a globally bounded classical solution;if,the solution of the system(1.1) will blow up [6].Whenn≥3,if Ω is a ball,then for arbitrarily small massm:=there exists(u0,v0)such that(u,v)blowing up[7].

Ever since 1970,mathematicians have intensively investigated different types of chemotaxis models for a variety of chemotaxis processes [2].When considering the logistic source,some researchers studied the corresponding quasilinear chemotaxis system of(1.1)

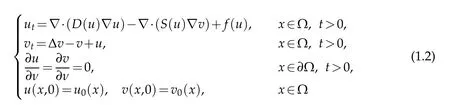
withD,S∈C2([0,∞))satisfyingD(s)≥c0sρ,c1sq≤S(s)≤c2sq.Whenf≡0,previous works have investigated whether the solutions are globally bounded or blow up [8–10].It is well-known that logistic sources favor the existence of the globally bounded solution.Indeed,iff(s) is a smooth function fulfillingf(0)≥0 andf(s)≤as−µs2for alls>0,it is shown that wheneverq<1,there exists a unique globally bounded and classical solution [11,12].Whenf(s)≤a−µs2for alls≥0,witha≥0 andµ>0 properly large,ifn≥3 and Ω is convex,Winkler [13] showed the global boundedness of solutions.The chemotaxis signal of(1.2)is produced directly by cells,yet the signal generation undergoes intermediate stages in some realistic biological processes[14–16],the indirect signal production mechanism can cause different interaction of cross-diffusion and the logistic source.The chemotaxis system with indirect signal production[16]was introduced

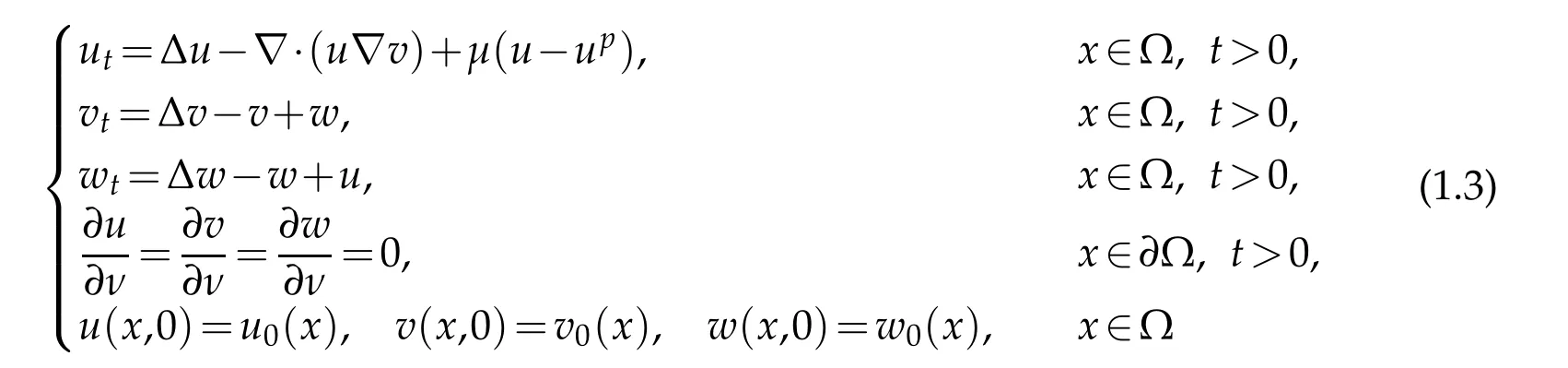
withµ>0,p>1.It was shown that ifthe solution is globally bounded;ifµ>0 is sufficiently large,(u,v,w)satisfies‖u(·,t)−1‖L∞(Ω)+‖v(·,t)−1‖L∞(Ω)+‖w(·,t)−1‖L∞(Ω)→0 ast→∞.

Wang[17] studied the more realistic nonlinear diffusion situation and came up with the following quasilinear fully parabolic chemotactic system with indirect signal production and logistic source

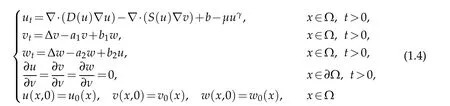
in a smooth bounded domain Ω ⊂Rn(n≥1) with homogeneous Neumann boundary conditions,where the parametersb≥0,γ,ai≥1,µ,bi(i=1,2)are assumed to be positive constants,νdenotes the outer normal derivative on∂Ω,the functionsD,S∈C2([0,∞))satisfy

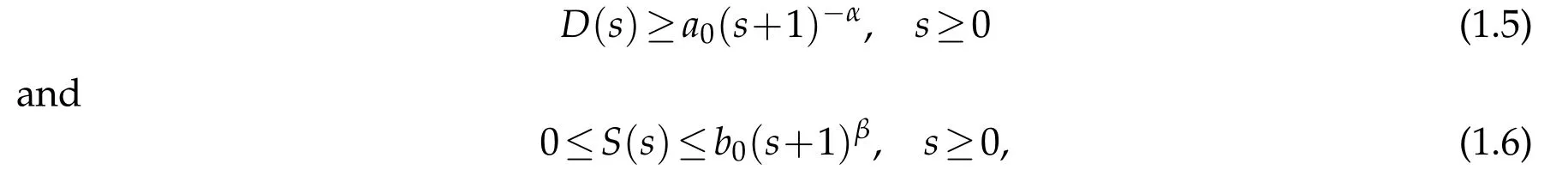
wherea0,b0>0 andα,β∈R are constants.The author considered the boundedness of solutions in (1.4),then he obtained the global boundedness of solutions in four cases:the self-diffusion dominates the cross-diffusion;the logistic source suppresses the crossdiffusion;forµ>0 sufficiently large,the logistic dampening balances the cross-diffusion;the self-diffusion and the logistic source both balance the cross-diffusion withµ>0 suitably large.

Inspired by the above works[15–17],in this paper,we further consider the asymptotic behavior of solutions to(1.4).

The main result of this paper reads as follows.

Theorem 1.1.Let γ≥1,Ω⊂Rn(n≥1)be a bounded domain with smooth boundary.Assume that D,S satisfy(1.5)and(1.6)with a0,b0>0,α,β∈R.Suppose that any nonnegative initialvalue0<ω<1.Then there exist b≥0andµ>0properly large,such that the global classical solution of(1.4)satisfies

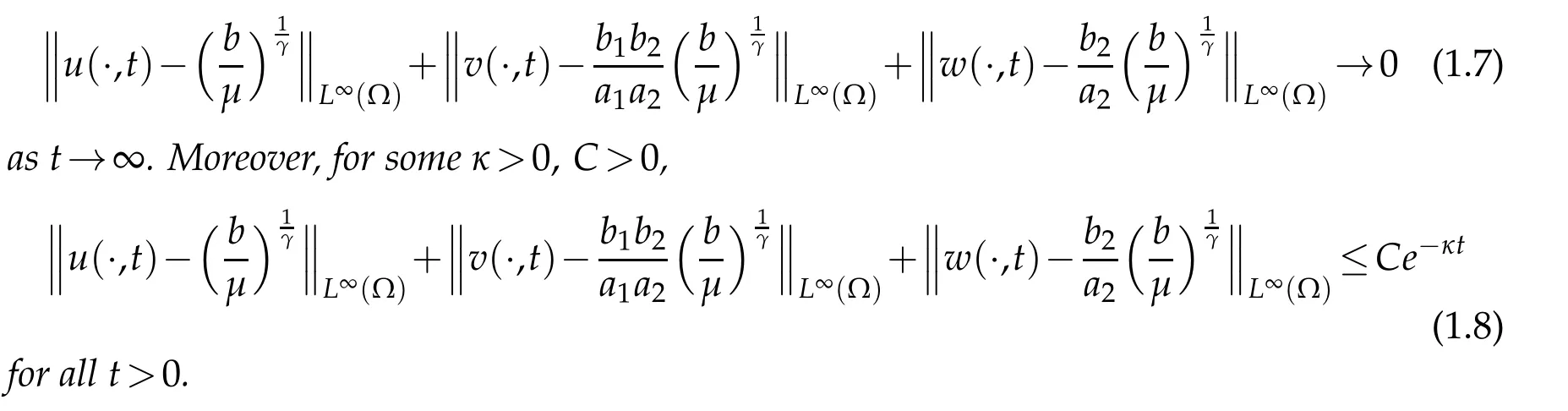
This paper is organized as follows.In Section 2,we obtain a lower bound foruby setting up an estimate of ∆vand using the comparison principles.In Section 3,we construct the corresponding energy function to prove Theorem 1.1.

2 A lower bound for u

To prove the main result,at the beginning,we give a lemma about the Laplacian in Ωwith homogeneous Neumann boundary conditions.

Lemma 2.1(Neumann Laplacian[16,18]).Let p∈(1,∞),λ∈(0,1).∆N shows the realization of the Laplacian in Lp(Ω)with domain

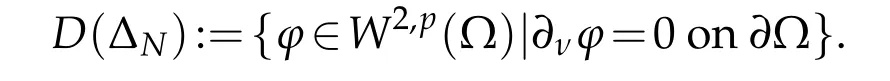
Then the operator A:=−∆+λ is sectorial and processes closed fractional powers Aδ for arbitrary δ>0with dense domain D(Aδ)known to have the embedding property

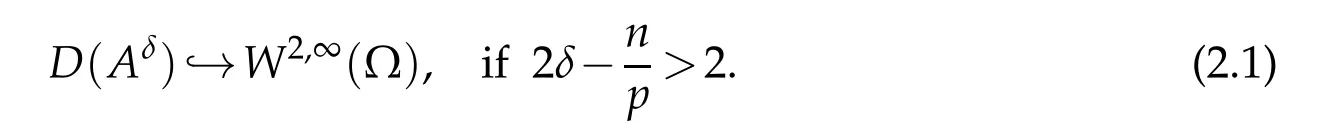
Furthermore,if(e−tA)t≥0represents the corresponding analytic semigroup,we can see that there exists a constant Cp,δ>0such that

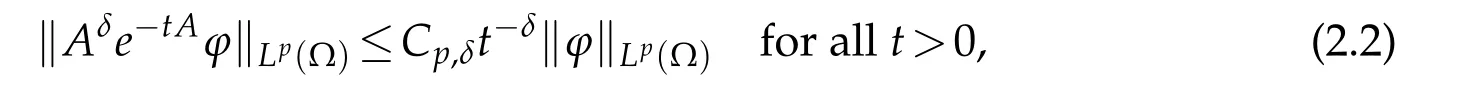
provided ϕ∈Lp(Ω).

Inspired by[19],then we establish an estimate of ∆vpromising the validity of a lower bound foru.

Lemma 2.2.Let γ≥1,δ0∈(0,1)and a2≥1.If(u0,v0,w0)∈Cω×W1,∞(Ω)×W1,∞(Ω),0<ω<1,and(u,v,w)is the solution of(1.4).Then for some p>1,there exists a constant C1>0independent of initial data such that

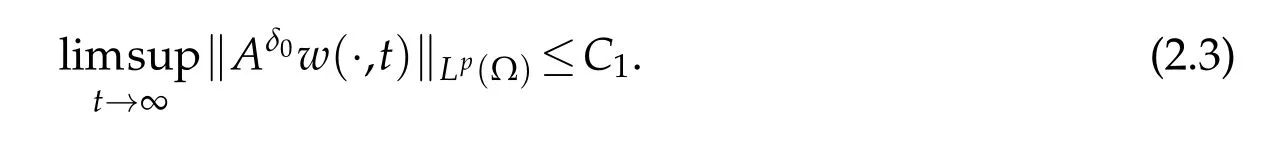
Proof.According to the globally bounded solution of(1.4),there existsC2such that

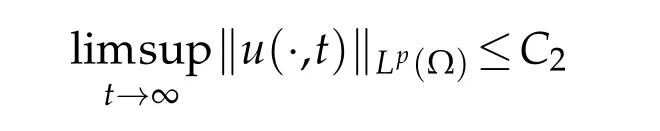
for allt>0.Then there exists suitably larget0=t0(u,v,w)>0 satisfying

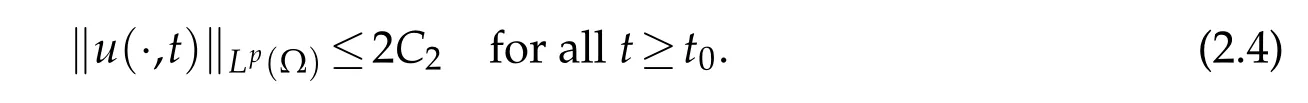
For the third equation in(1.4),by means of the variation-of-constants representation,we have

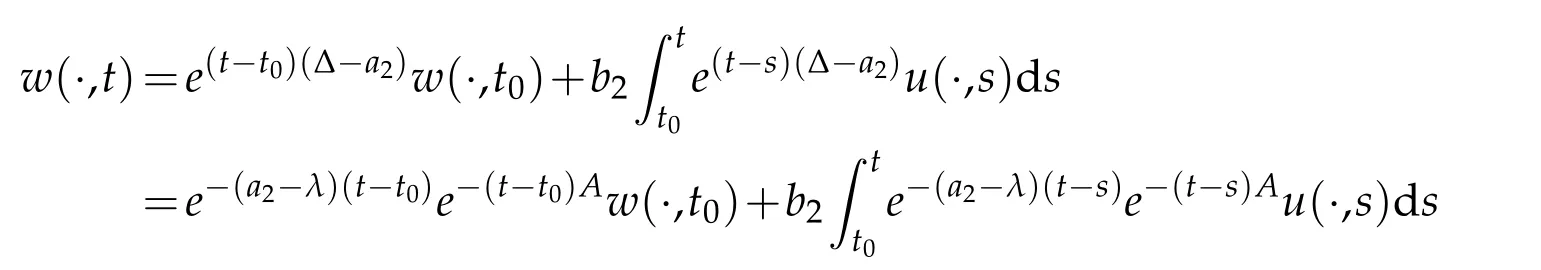
for allt∈(t0,∞).In view of(2.2)and(2.4),we can see that

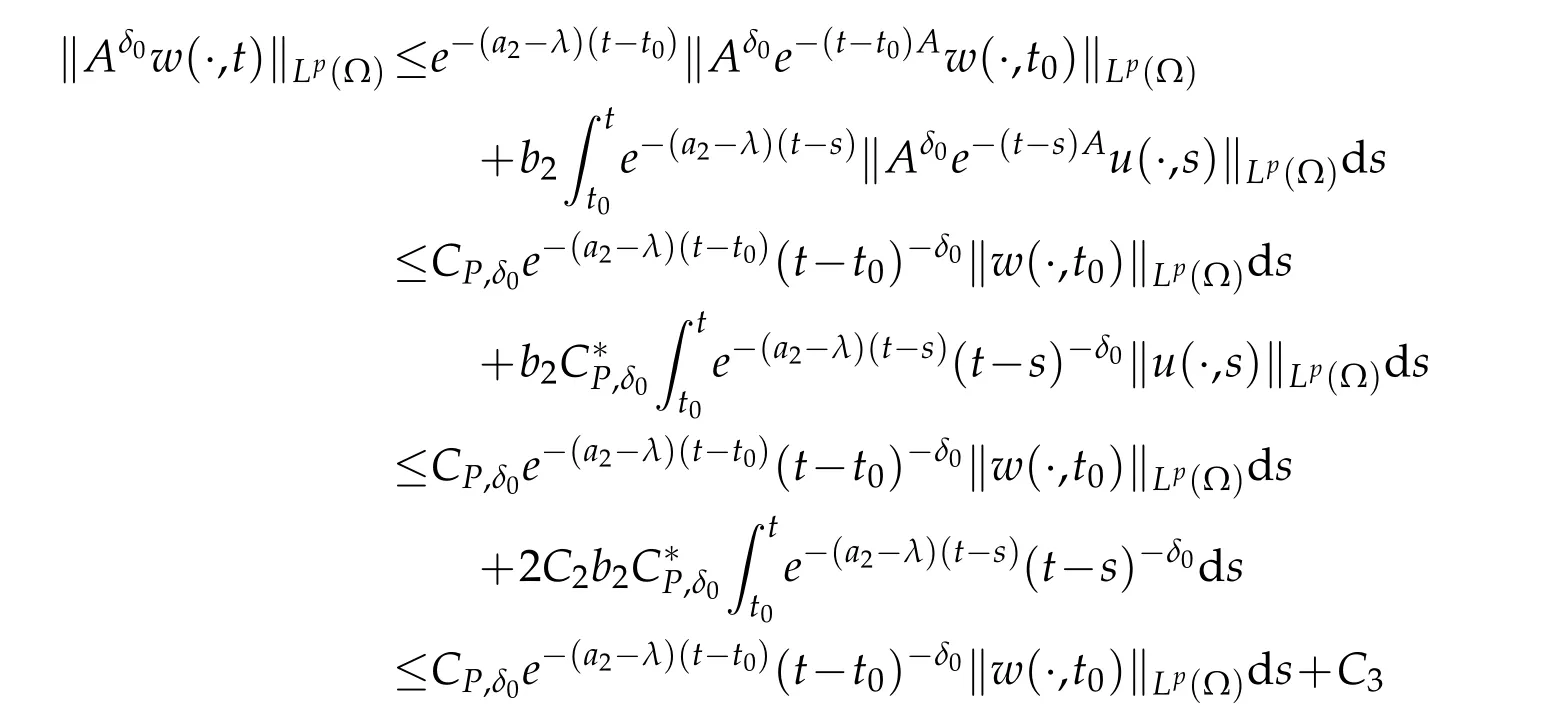
for allt∈(t0,∞),whereC∗P,δ0>0 anddσ<∞on the condition thatδ0∈(0,1)anda2≥1.Thereafter,

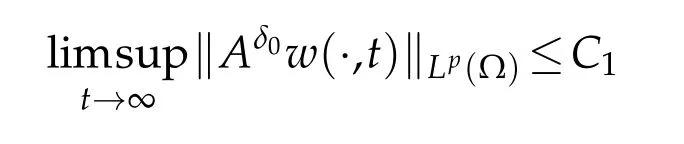
with someC1>0.

Lemma 2.3.Let γ≥1,a1≥1.If(u0,v0,w0)∈Cω×W1,∞(Ω)×W1,∞(Ω),0<ω<1,and(u,v,w)is the solution of(1.4),we can choose a constant C∗>0independent of initial data such that

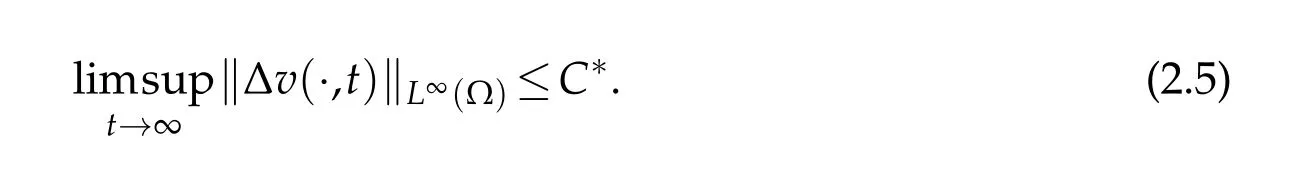
Proof.According to(2.3),then there existst0=t0(u,v,w)>0 satisfying

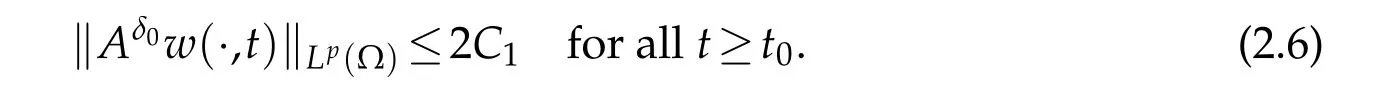
In addition,let us fix anyδ1∈(1,2) satisfyingδ1−1<δ0<1 and choosep>1 satisfyingthen

Employing the variation-of-constants representation forv,we obtain

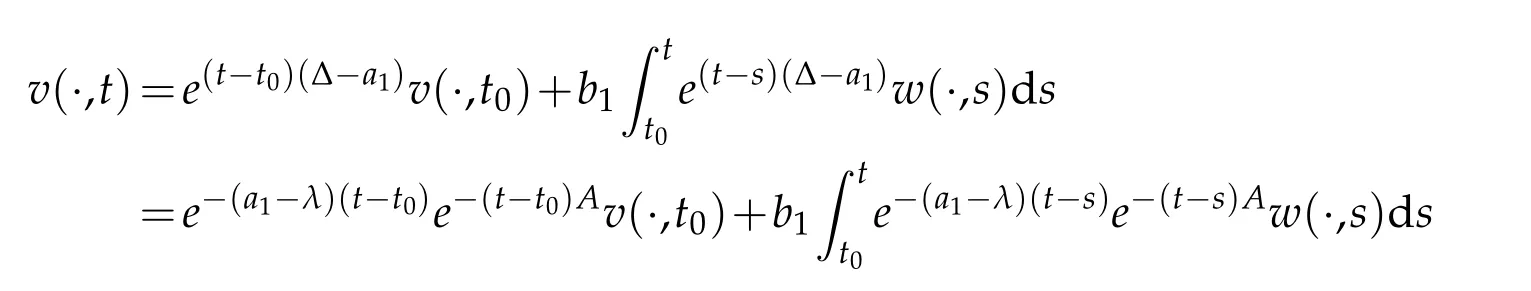
for allt≥t0.Combining(2.1),(2.6)and(2.7),we can write

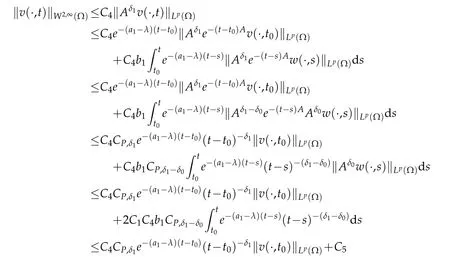
for allt∈(t0,∞),wheredσ<∞on the condition thatδ1−δ0∈(0,1)anda1≥1.Thereafter,

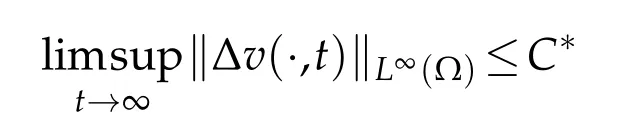
with someC∗>0.

Lemma 2.4.Let γ≥1.If(u0,v0,w0)∈Cω×W1,∞(Ω)×W1,∞(Ω),0<ω<1,and(u,v,w)is the solution of(1.4).Assume that D,S satisfy(1.5)and(1.6),then there exists a constant b∗>0such that if b>b∗,thus

Proof.According to(2.5),we can see that there existst0=t0(u,v,w)>0 satisfying

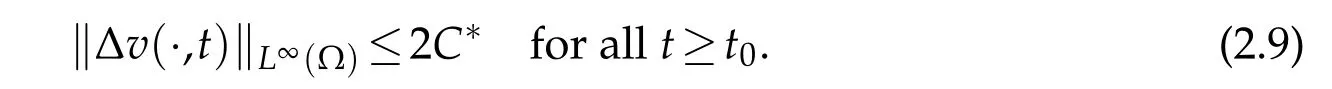
Letb>b∗:=max{2γC∗b0,2βC∗b0+2β−1µ},we shall treat the first equation of(1.4)in two cases:γ≥βandγ<β.

Whenγ≥β,the first equation of(1.4)infers that

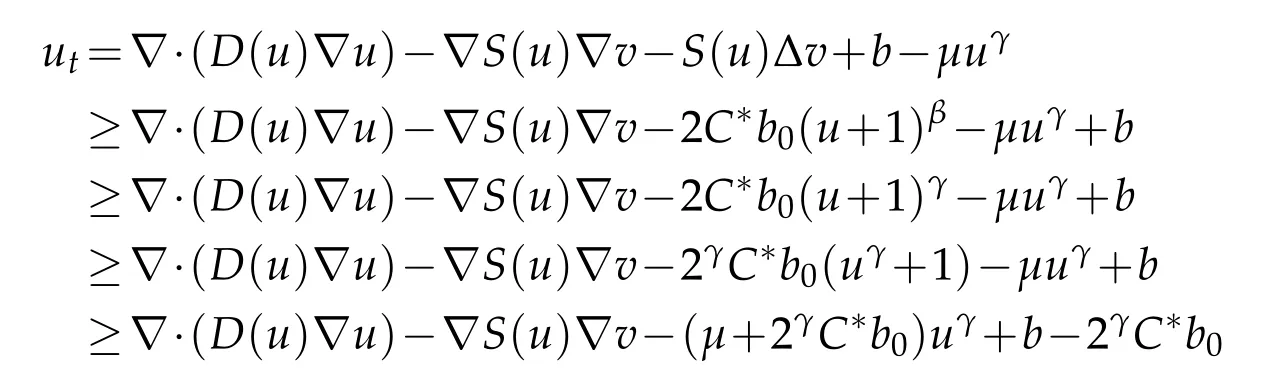
for allx∈Ω,t≥t0.Assume that the functiony(t)∈C1([t0,∞))satisfies

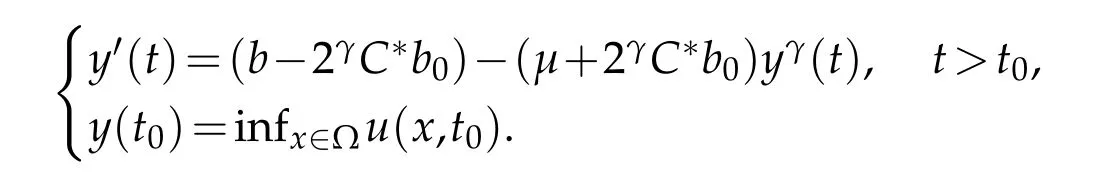
Therefore,relying on the comparison principle[19],we can write

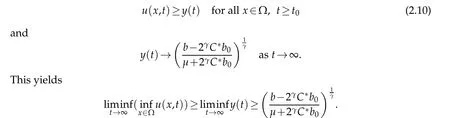
Whenγ<β,the first equation in(1.4)infers that

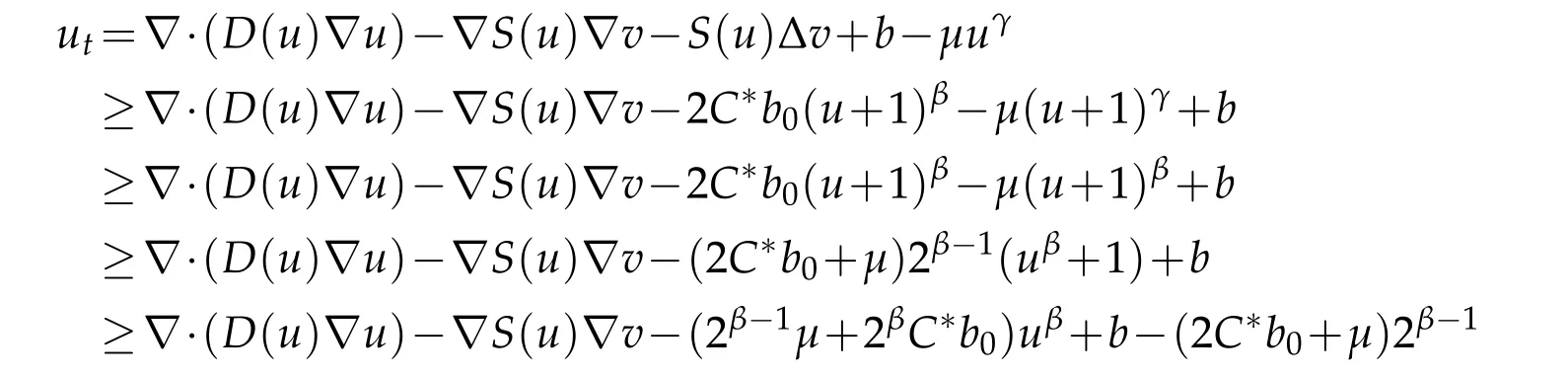
for allx∈Ω,t≥t0.Suppose that the functiony(t)∈C1([t0,∞))satisfies

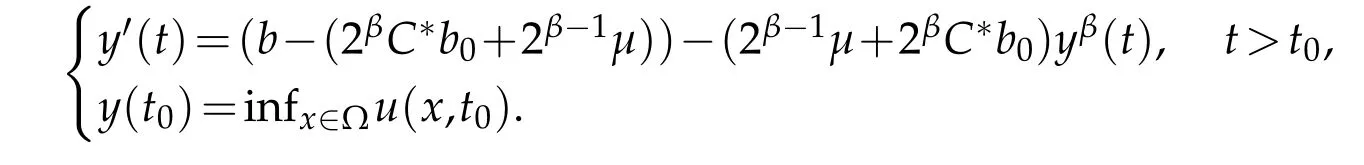
Therefore,using the comparison principle,we can see that

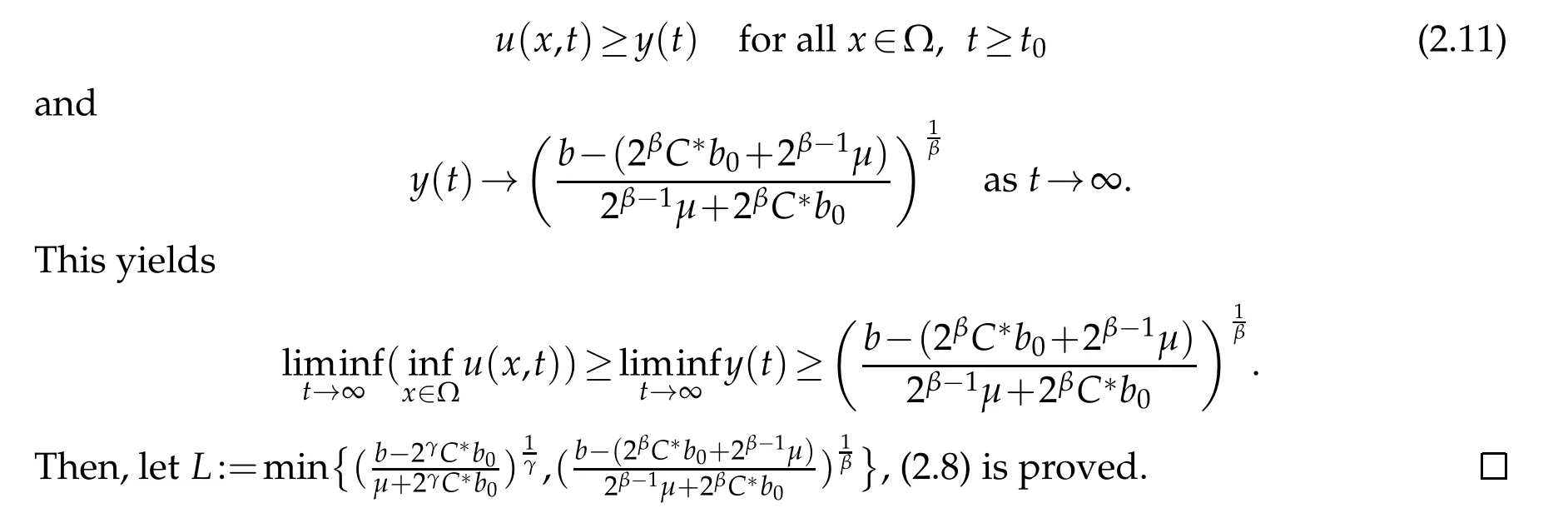
3 Asymptotic behavior

First,the following lemma from elementary analysis[20]is a useful tool in this section.

Lemma 3.1.Let f:(1,∞)→[0,∞)be uniformly continuous such thatThen

We next construct an appropriate energy function to(1.4),the energy function is prepared for the proof of asymptotic behavior.According to the parabolic regularity [21]with the global boundedness of(u,v,w),we conclude that there existρ∈(0,1)andH>0 such that

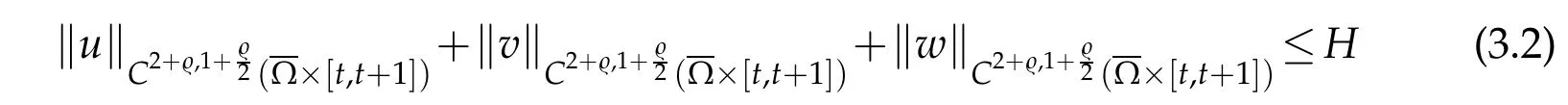
for allt>1.We letψ:(0,∞)→R be defined by

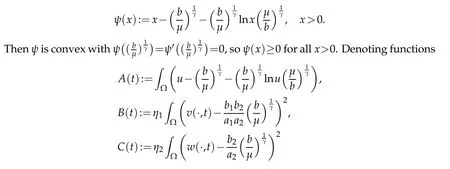
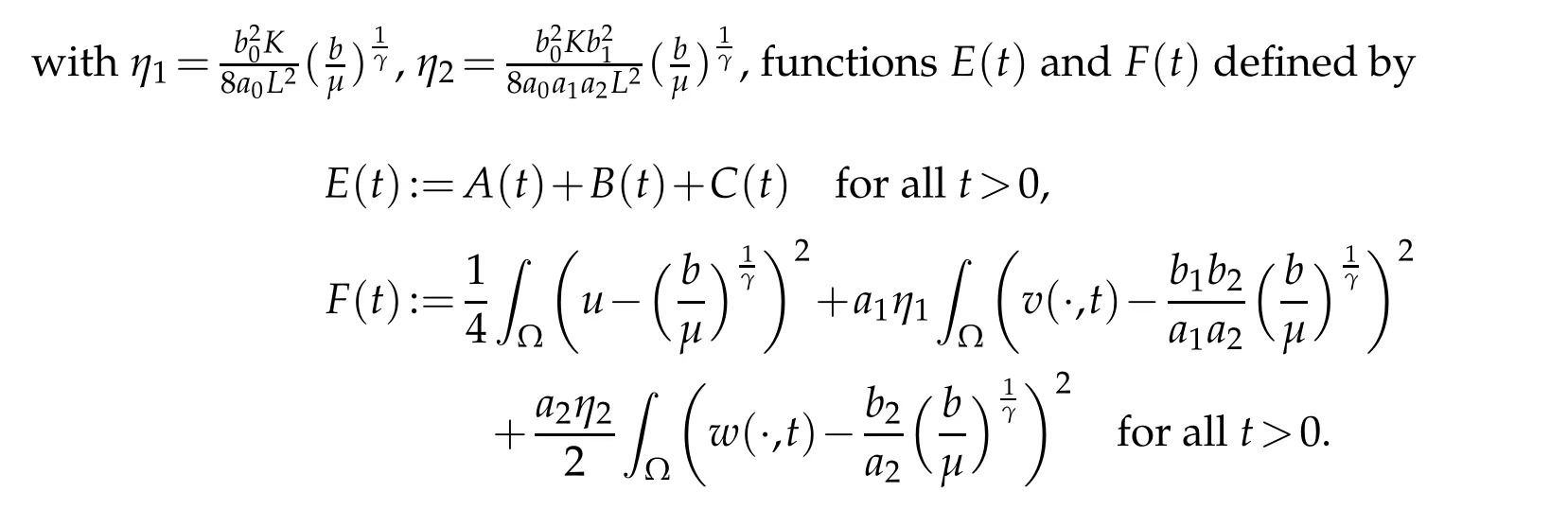
Lemma 3.2.Let γ≥1.If(u0,v0,w0)∈Cω×W1,∞(Ω)×W1,∞(Ω),0<ω<1,and(u,v,w)is the solution of(1.4),and D,S satisfy(1.5)and(1.6).Then there exist b≥0andµ>0properly large,such that the functions E(t)and F(t)satisfy

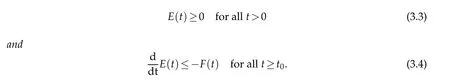
Proof.Notice thatE(t)≥0 is obvious.In terms of the first equation in(1.4),we obtain

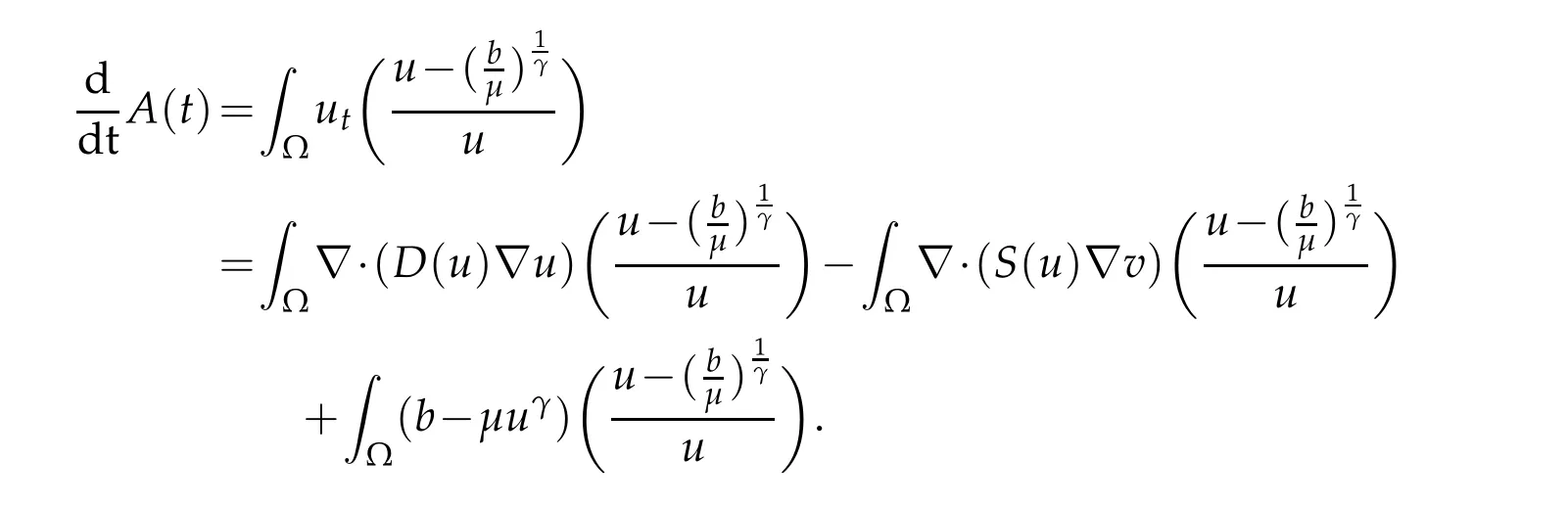
In terms of the globally bounded solution of(1.4),we can see that(u+1)2β+α≤Kfor eachα,β∈R,t>0.Using integration by parts,the mean value theorem,Young’s inequality and(u+1)2β+α≤K,we have

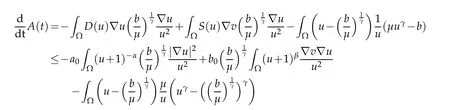
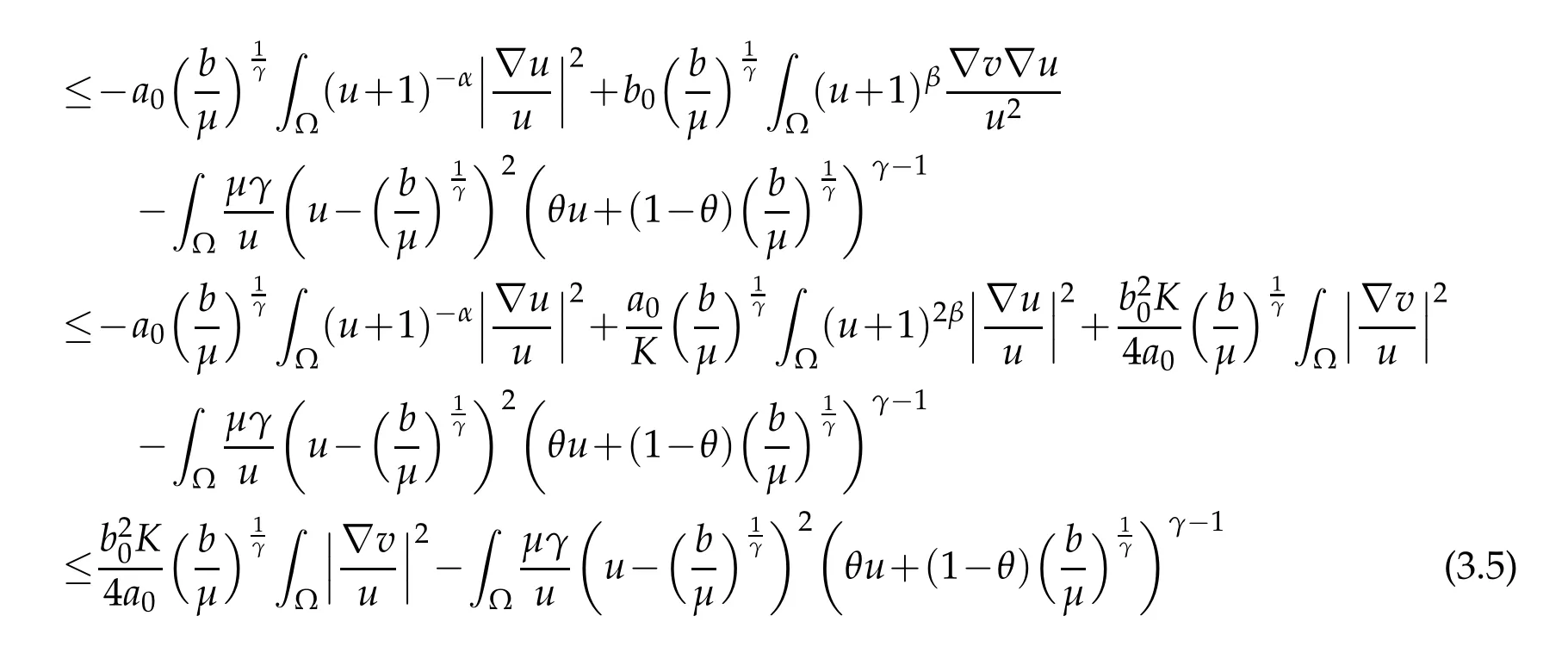
withθ=θ(x,t)∈(0,1) for allx∈Ω andt>0.Using the second equation of(1.4),we can see that

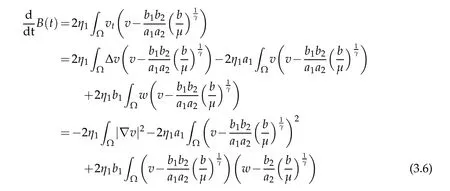
for allt>0.Using the third equation in(1.4),we can write

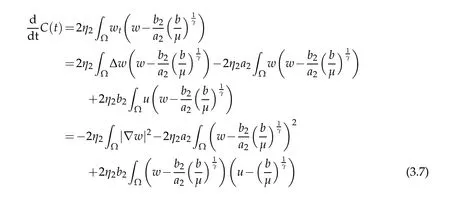
for allt>0.Hence,collecting terms above(3.5)-(3.7),we get

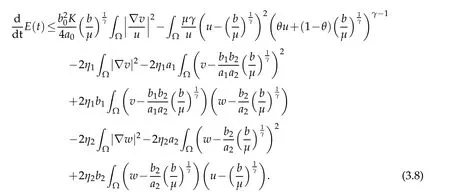
In terms of(3.8),using Young’s inequality and(2.8),we have

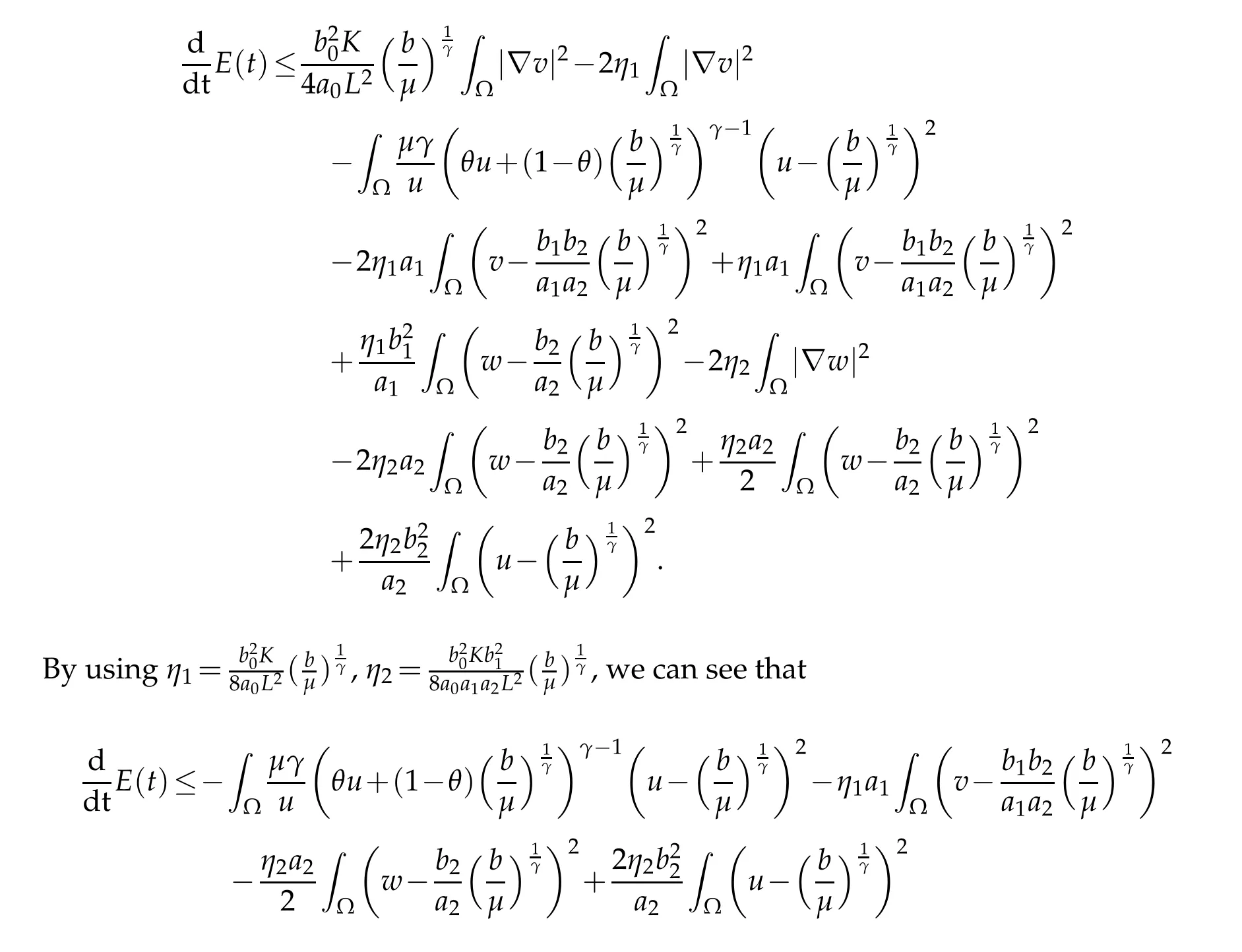
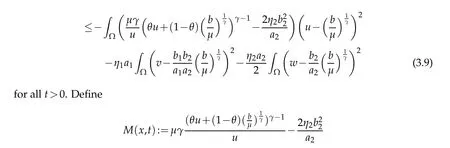
withθ=θ(x,t)∈(0,1)for allx∈Ω andt>0,we could split into two casesγ≥2 and 1≤γ<2 to arrive at the estimate.

Ifγ≥2,in light of Lemma 2.4,there existst0>0 suitably large such that

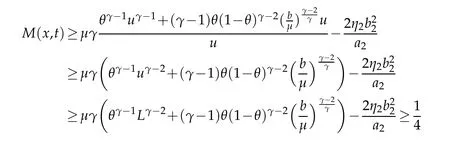
withx∈Ω,t≥t0for allµ>µ1.

If 1≤γ<2,in light of(2.4)and Lemma A.1[22],there existsµ1>0 suitably large such thatM(x,t)≥1/4.Combining with(3.9),we complete the proof of(3.4).

We are now in the position to prove our main result.

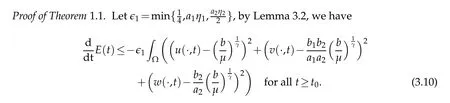
Integrating(3.10)fromt0to ∞,we obtain

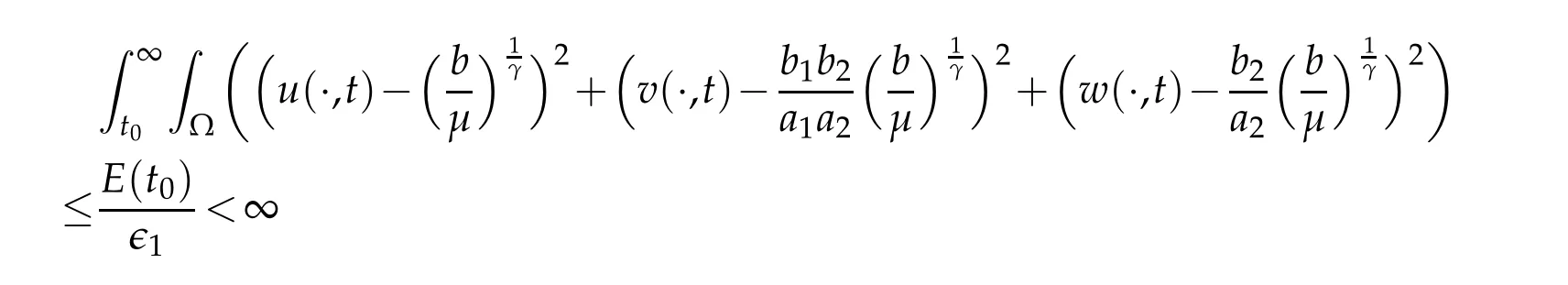
Acknowledgments

The paper is supported by the National Science Foundation of China(11301419)and the Meritocracy Research Funds of China West Normal University[17YC382].