零模关于一致模的条件分配性方程
2021-10-18侯晓东张继鹏
侯晓东 张继鹏
(泰山科技学院 数理教学部,山东 泰安 271000)
聚合算子广泛应用于多个领域,如:人工智能、信息融合及决策理论。条件分配性[1-8]作为两个聚合算子之间的一个重要性质,极具研究价值。作为信息论最优化中比较直接的应用,伪分析通常要求算子之间要满足一定的条件分配性方程[9,10]。
一致模和零模作为三角模、三角余模的两种推广,研究领域如:不同类一致模的结构、特征刻画、有关的吸收方程以及函数方程等。文献[9,10]研究了零模关于一致模的条件分配性方程:
F(x,U(y,z))=U(F(x,y),F(x,z)),x、y、z∈[0,1],0 关于零模F 关于一致模U的条件分配性方程: F(x,U(y,z))=U(F(x,y),F(x,z)),x、y、z∈[0,1],0 文献[11]已给出取小、取大一致模时的完整解。在此基础上,本文讨论带有连续、阿基米德基础算子的一致模类的条件分配性方程。 本节给出文中涉及到的概念及结论。 定义1:若二元函数U:[0,1]2→[0,1],对于任意x、y、z∈[0,1]满足下列条件: (1)U(x,y)=U(y,x), (交换性) (2)U(x,U(y,z))=U(U(x,y),z), (结合性) (3)U(x,y)≤U(x,z),y≤z (单调性) (4)U(e,x)=x, (单位元e∈[0,1]) 称U为一致模,e 为一致模U的单位元。当e=1 时,一致U退化为三角模T;当e=0 时,一致模U退化为三角余模S。若U为带有单位元e∈]0,1[的一致模,根据定义可构造二元函数TU、SU:[0,1]2→[0,1]:[12]: 分别记公式(1)中的一致模为Umin,公式(2)中的一致模为Umax。 定理3:设U是带有单位元e∈]0,1[的一致模。TU与SU均为严格的,则下列之一成立: (i)U∈Umin;(ii)U∈Umax;(iii)U是可表示一致模; 定理4:设U是带有单位元e∈]0,1[的一致模。TU为严格的,SU为幂零的,则下列之一成立: (i)U∈Umin;(ii)U∈Umax; 定理5:设U是带有单位元e∈]0,1[的一致模。TU为幂零的,SU为严格的,则下列之一成立: (i)U∈Umin;(ii)U∈Umax; 定理6:设U是带有单位元e∈]0,1[的一致模。TU与SU均为幂零的,则下列之一成立: (ii)U∈Umin;(ii)U∈Umax。 下面介绍零模的概念及相关结论。 定义7[13]:设二元函数F:[0,1]2→[0,1],满足交换性、结合性、非递减性,并且存在吸收元k∈[0,1],即: F(k,x)=k,x∈[0,1],F(0,x)=k,其中x≤k;F(1,x)=k,其中x≥k; 称F 为零模。显然,当k=0 时,零模F 退化为三角模T;当k=1时,零模F 退化为三角余模T。 定理2.12[13]:设F 是带有吸收元k∈]0,1[的零模,则F 的结构如下: 其中:T为三角模,S为三角余模。 基于具有连续基础算子的一致模,在给定基础算子类型的条件下研究方程: F(x,U(y,z))=U(F(x,y),F(x,z)),x、y、z [0,1],0 讨论如下三种情况:TU和SU为幂等的或者阿基米德的;TU=min 且SU为连续的; TU为连续的且SU=max。 定理2.1:设F 是带有吸收元k∈]0,1[的连续零模,一致模U具有连续基础三角模TU和基础三角余模SU,单位元e∈]0,1[。若连续零模F 与一致模U满足条件分配性方程: F(x,U(y,z))=U(F(x,y),F(x,z)),x、y、z [0,1],0 (i)e 其中:T2*是连续三角模,T2**是严格三角模,S2*和S2**是连续三角余模,S*是幂零三角余模,并且幂零三角余模S*中满足s(1)=1的加法生成子也是严格三角模T2**的乘法生成子。 (iii)e 因此,e 是零模F 的幂等元,从而其基础三角余模SF具有序和结构。 ②区间[e,k]是一致模U的幂等元。令x∈]0,1[,y=z=e,代入(3)得 F(x,e)=F(x,U(e,e))=U(F(x,e),F(x,e))。 由于F 是连续的,{F(x,e):x∈[0,1]}=[e,k]均是U的幂等元。所以,SU具有序和结构,对任意的(x,y)∈[0,e]2]k,1]2,有U(x,y)=max(x,y)。 由于TU=min,所以对任意的(x,y)∈[0,e]2,有U(x,y)=min(x,y),SF是连续三角余模。 ③接下来讨论当(x,y)∈[k,1]2时,零模F 和一致模U 的结构。若存在a∈]k,1[是U的幂等元,则对任意的x∈]k,1[,有 F(x,a)=F(x,U(a,a))=U(F(x,a),F(x,a)), 由于F 是连续的,{F(x,a):x∈[k,1]}=[k,a]都是U的幂等元。 若a=1,则x∈[k,1]是U 的幂等元:任意的(x,y)∈[e,1]2,有SU(x,y)=max(x,y)。由于任意的三角模都关于SU(x,y)=max(x,y)分配,所以TF为任意连续三角模。 若存在一致模U的最大非平凡幂等元a<1,则(ii)成立。 反之,通过计算得知:若零模F 和一致模U具有上述定理中的任何一种形式,则(3)显然成立。同理可证其它结论成立。 本文讨论一类连续零模关于一致模的条件分配性方程,其中U为带有连续阿基米德基础算子的一致模。我们证明了基础三角余模TU=min 和基础三角余模SU=max时方程的非空解。在未来的工作中,我们计划讨论上述结论效用理论中的应用[13]。1 预备知识


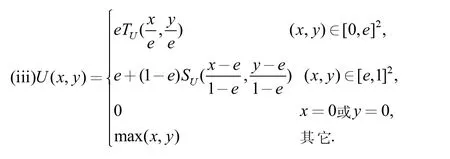


2 主要结论

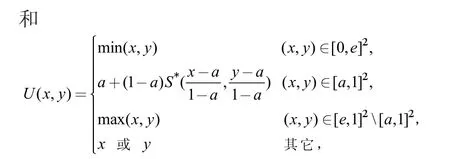



3 结论
