许 晶

（集宁师范学院 数学与统计学院，内蒙古 乌兰察布012000）

0 引言

Hamilton系统是一种经典的动力学系统，自从1834年Hamilton为了研究几何光学而建立后，被广泛地应用到天体力学、物理学、数学等各个领域，逐渐成为科学家们研究的热点.常见的Hamilton系统有经典Hamilton系统、广义Hamilton系统、自治Hamilton系统、无穷维Hamilton系统.近年来，很多学者致力于研究Hamilton形式的反问题和属性，及其在物理、力学方面的应用等相关内容.2009年，高强和钟万勰给出了Hamilton系统基于辛矩阵乘法显式时不变正则变换和时变正则变换，通过引入含参变量的近似Hamilton系统，并以该系统为基础进行辛矩阵乘法的正则变换，从而实现Hamilton系统既保辛又保能量的算法［1］.2014年，Mahomed等人通过Hamilton系统的首次积分使方程得以降阶，得到方程的封闭解［2］.2017年，蒋宪宏等人以Hamilton系统的正则变换和生成函数为基础，研究了线性时Hamilton系统边值问题的保辛算法，该方法保持了Hamilton系统原有的特性［3］.

本文选取无穷维Hamilton系统作为研究对象，利用一定变换，获得Hamilton正则形式.获得该形式的方法一般来说有几种，一种是Lagrange泛函方法，运用Legendre变换，确定Hamilton泛函，进而完成Hamilton正则化，该方法也被称为获得Hamilton系统的经典方法；其次是由Olver提出的全Hamilton函数法，该方法主要是依赖于乘法算子，并借助Hamilton函数，获得Hamilton形式；最后是代数方法，该方法主要结合了高等代数中的带余除法，避开了求Lagrange泛函这一难题.文献［4］由阿拉坦仓等人首次提出利用矩阵多元多项式的带余除法获得Hamilton正则形式，在其博士论文中也有阐释［5］，文献［6］和［7］是在以上基础上，先设定Hamilton算子的形式，根据已知算子的形式，得到关于Hamilton算子的方程组，进而得到Hamilton正则形式，除以上几种方法外，还由利用Lax对获得Hamilton正则形式，以及迹恒等式的方法等.

本文是在文献［4］的基础上，在没有事先设定Hamilton算子的情况下，针对代数方法进行分析，将一类偏微分方程通过带余除法，令余式为零，讨论Hamilton算子，给出Hamilton算子所满足的方程组，实现机械程序化，从而获得无穷维Hamilton线性正则形式.

1 预备知识

本文考虑微分方程系统：

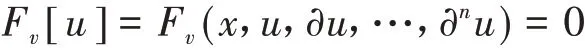
该系统是N个n阶微分方程组成，其中，v=1，…，N.自变量x=(x1，x2，…，xk)，因变量u=(u1，u2，…，um)，∂nu表示u对x的n阶偏导数.

定义1［6］称如下发展方程（组）为无穷维Hamilton正则系统为变分导数.

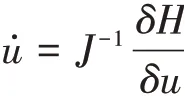
无穷维Hamilton正则系统分为线性无穷维Hamilton正则系统和非线性无穷维Hamilton正则系统，由Vainberg［8］定理可知，线性Hamilton系统可以简化成如下分离变量的形式.

定义2［6］设X是Hilbert空间，H：D（H）⊂X×X→X×X为线性微分算子，如果H满足H*=JHJ，则称发展型方程（组）

注释1若发展方程（组）式（1）中H不显含x，式（1）为“∂/∂x”-型Hamilton正则系统，式（1）转化为如下形式：

若发展方程（组）（1）式中H不显含t，式（1）为“∂/∂t”-型Hamilton正则系统，式（1）转化为如下形式：在本文中，主要讨论的是第一种形式.

定义3［6］给定微分函数P(x，u(n))，其i阶全导数的一般形式：

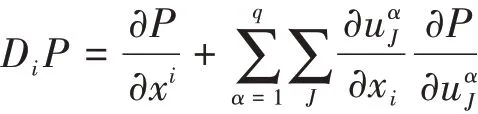
其中，J=（j1，…，jk），且有特别的，对于P（xi，u（n）），相应的坐标为xi=(x，t)，其全导数引理1［5］一元n次多项式对于因子(x-h)的整除关系表示

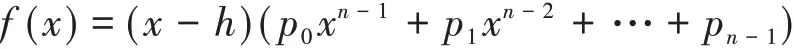
从而比较左右指数相等项的系数，获得p0，p1，…，pn-1.

算子

2 方法简介

依据文献［4］，并利用引理1，对矩阵的带余除法做了进一步的推广，并给出将微分方程转化到Hamilton系统下的机械化方法，具体步骤如下：

步骤（2）：无穷维线性Hamilton正则系统形式为ω̇=Hω，令Hamilton系统的矩阵多元多项式为：

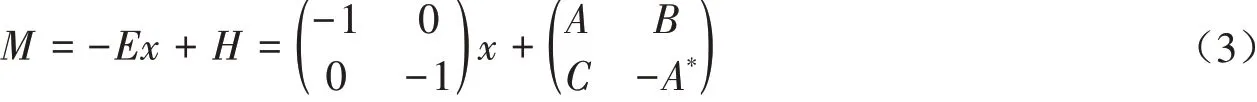
步骤（3）：通过带余除法，令Δ=MQ+R，有

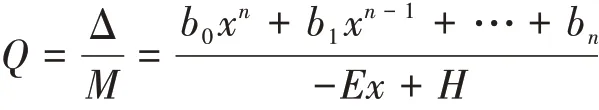
即Q=-b0xn-1-(Hb0+b1)xn-2-…-(Hn-1b0+Hn-2b1+…+bn-1)，从而得到余式R的表达式：

R=Hnb0+Hn-1b1+…+Hbn-1+bn（4）

步骤（4）：为了能够整除，令R=0，即可得到Hamilton算子中A，B，C，A*，从而，得到了该微分方程的Hamilton正则形式ω̇=Hω.

注释2在此，我们讨论H算子的四阶形式，即：

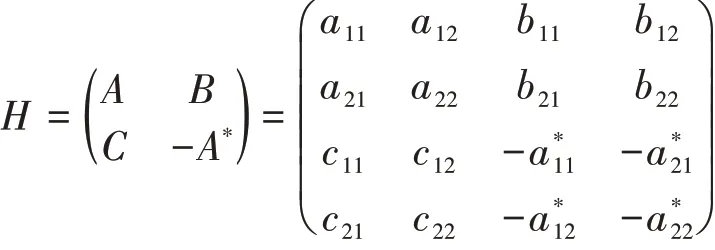
不妨记其中，H1=H.

由余式R=0可知，Hamilton算子满足以下方程组，

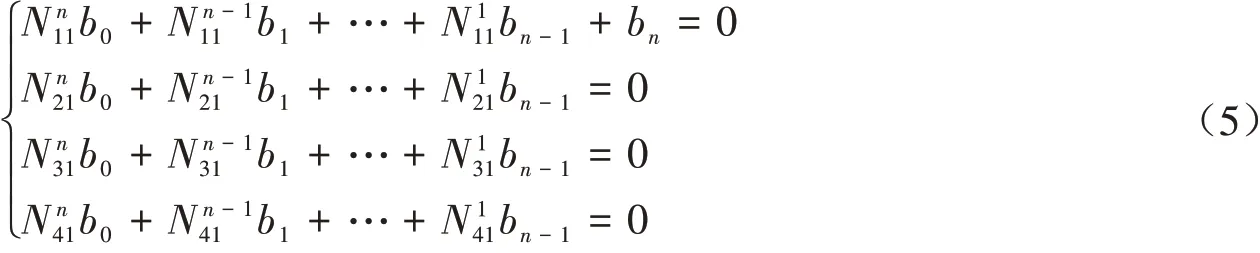
通过以上关系式，可以获得Hamilton正则形式.

3 具体算例

以下算例均为当Hamilton算子为二阶形式，无法获得Hamilton正则方程的时候，作者尝试了由二阶升四阶的处理方式，从而获得了新的Hamilton正则形式.

例1：考虑热传导方程ut=uxx的Hamilton正则表示.

解：令Δ=uxx-ut，其矩阵形式为：

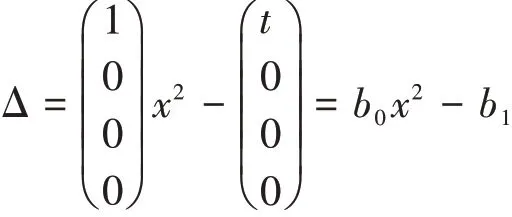
Hamilton系统的矩阵多元多项式：

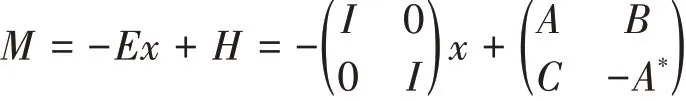
其中，

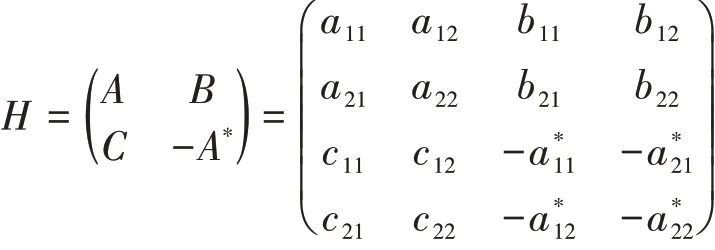
故有Δ=MQ+R，其中余式R=H2b0-b1=0，由式（5）进一步展开，得：

I’m forever on a diet, since I put on weight easily.我永远都在减肥，因为我很容易长胖。

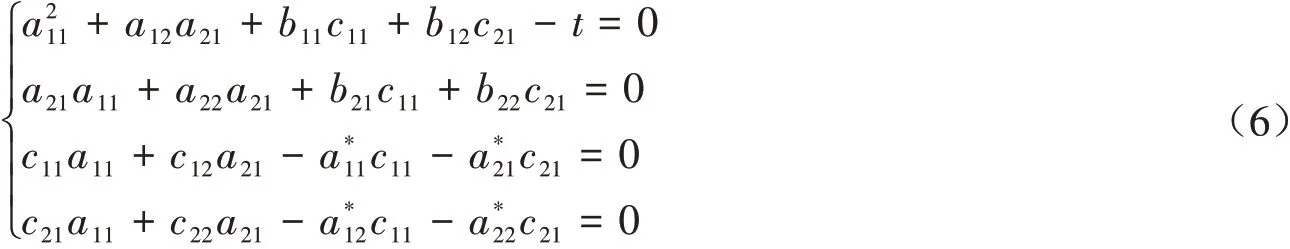
方程组（6）有很多组解，由此根据A，B，C，-A*的不同形式获得不同H算子，从而得到方程的Hamilton正则形式，不妨假设H算子为准对角形式，即B=C=0，式（6）变化为：

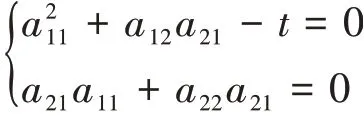
当a11=a22=0，a12=-1，a21=-Dt时，有

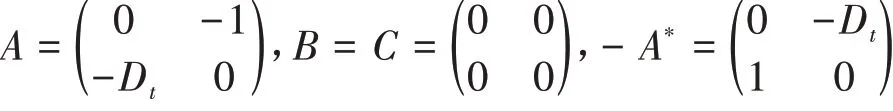
Hamilton正则表示如下：

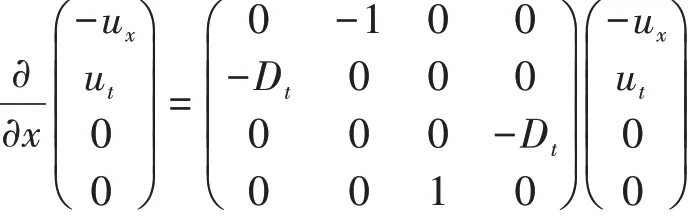
例2：考虑Burgers方程uxx+uux-ut=0的Hamilton正则表示.

解：令Δ=uxx+uux-ut，其矩阵形式为：

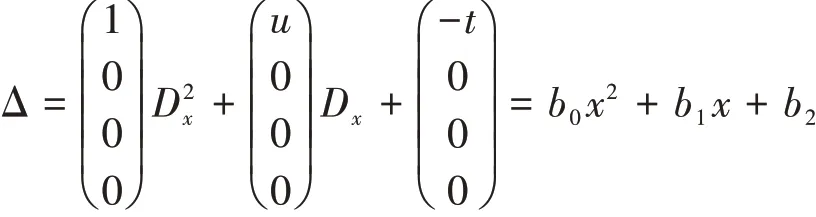
Hamilton系统的矩阵多元多项式：

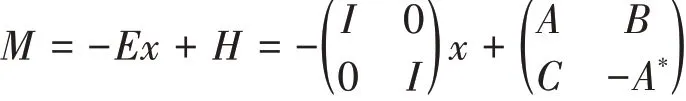
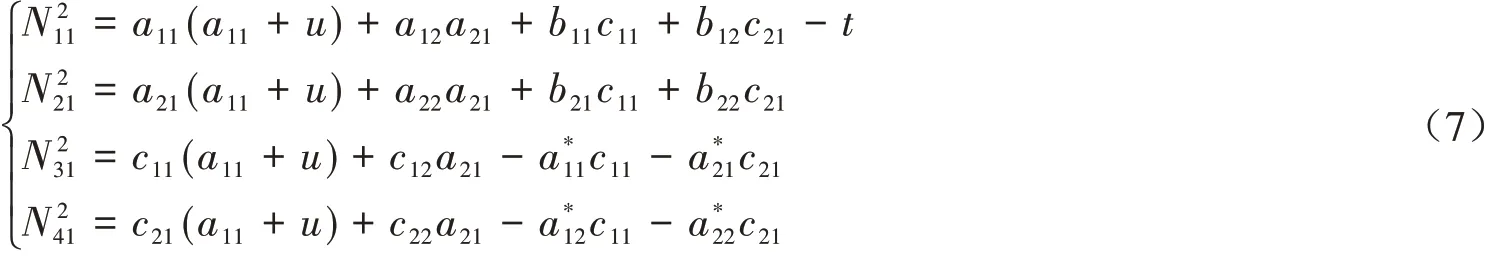
利用带余除法，令余式R=H(Hb0+b1)-b2=0，式（5）变化为：方程组（7）有很多组解，由此根据A，B，C，-A*的不同形式获得不同H算子，从而得到方程的Hamilton正则形式，不妨假设H算子为准对角形式，即B=C=0，式（6）变化为：

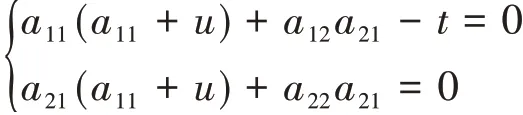
令a11=-u，a22=0，a12=1，a21=Dt，得到该方程的Hamilton正则形式：

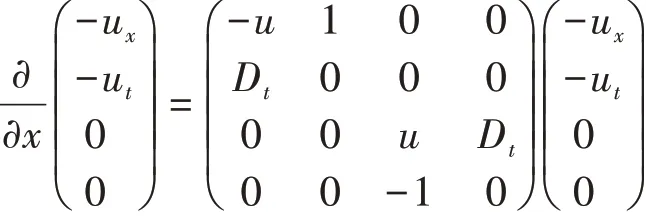
以上两个例子并不是只有一种结果，根据Hamilton算子的不同形式，A，B，C，A*满足不同关系，可以获得不同结果，本文提供了获得Hamilton算子的一种方法，尤其对于Hamilton算子为二阶行不通的时候，可以尝试升阶作进一步处理.

综上所述，该方法的核心是把微分多项式转换为算子多项式，利用矩阵多元多项式的运算形式，从而将微分方程因式分解后得到Hamilton正则形式.

4 结束语

本文主要针对代数方法进行分析，通过阅读并整理资料，以Hamilton算子为四阶的形式作为探究对象，将一类偏微分方程利用带余除法，令余式为零，讨论Hamilton算子，给出Hamilton算子所满足的方程组，在一定程度上实现了机械程序化.其优势一是当Hamilton算子为二阶形式，但又得不到解的时候，通过升阶的处理，为Hamilton算子的获得提供一条思路；二是简单，易操作，甚至只利用一些高等代数的知识即可实现，对于数学方面的本科生如作偏微分方程的一些训练，不失为一块较好的例子.本人知识有限，该方法的缺点在于由于得到Hamilton算子是以方程组的形式出现，解该方程组时，只能得到一部分解，因此也只能得到部分Hamilton算子，如果能够将该方法作一些处理，从而扩大获得Hamilton算子的形式，是本人应该做的一部分工作.