李文静 贾美美 †

（1.内蒙古工业大学电力学院，呼和浩特010080）（2.内蒙古自治区机电控制重点实验室，呼和浩特010051）

引言

1963年，Lorenz提出了Lorenz混沌系统，其混沌吸引子的拓扑结构与蝴蝶的形状十分相似，是一种双翅膀混沌系统，该系统的提出掀起了混沌研究的热潮［1］.混沌在保密通信［2-5］、图像加密［6-8］等领域具有良好的应用前景.为了将混沌更好地应用于保密通信，人们长期致力于研究具有复杂拓扑结构和丰富动力学行为的混沌系统，例如单方向多翅膀混沌系统和多方向网格多翅膀混沌系统.由于单方向多翅膀混沌系统和多方向网格多翅膀混沌系统具有多个可调参数，即数量众多的翅膀能在相空间中呈现单个方向分布甚至多个方向分布的网格状图案，各个翅膀之间具有互相嵌套的拓扑结构，翅膀的数量、大小及网格状分布的图像可以由可调参数来进行调节，具有更复杂的动力学行为.这种复杂性体现在混沌吸引子的相轨迹或状态变量的取值能在多个翅膀之间随机的跳变，从而使得当翅膀的数量越多时，这种跳变的随机性就越大，更有利于混沌加密［9，10］.因此，基于双翅膀混沌系统构造多翅膀混沌系统具有重要意义.

2008年，Yu等［11］采用符号函数基于广义双翅膀Shimizu-Morioka（S-M）混沌系统构造了单方向多翅膀混沌系统和二方向网格多翅膀混沌系统.2010年，Yu等［12］采用符号函数基于广义双翅膀S-M混沌系统、双翅膀Lü混沌系统、双翅膀Chen混沌系统、双翅膀Sprott-1混沌系统和双翅膀Sprott-2混沌系统构造了相应的单方向多翅膀混沌系统.2012年，周欣等［13］采用符号函数基于广义双翅膀Lorenz混沌系统构造了二方向网格多翅膀混沌系统.2015年，Huang等［14］采用分段时滞函数基于双翅膀Lorenz混沌系统构造了二方向网格多翅膀混沌系统.2016年，孙克辉等［15］采用符号函数基于简化双翅膀Lorenz混沌系统构造了二方向网格多翅膀混沌系统.2018年，Zhang等［16］采用锯齿波函数和阶梯函数基于提出的双翅膀混沌系统构造了二方向网格多翅膀混沌系统.2018年，Yu等［17］采用阶梯切换函数基于双翅膀Lorenz混沌系统构造了三方向网格多翅膀混沌系统.

2016年，Zhou等［18］采用符号函数与光滑磁控忆阻器基于改进的双翅膀Lü混沌系统构造了单方向多翅膀混沌及超混沌系统.文献［19-21］也报道了如何采用忆阻器来构造多翅膀混沌及超混沌系统.文献［11-17］采用的符号函数、分段时滞函数、锯齿波函数、阶梯函数、阶梯切换函数都是非光滑函数，其构造的多翅膀混沌或超混沌系统都是非光滑系统.然而，构造光滑多翅膀混沌系统和超混沌系统更加具有挑战性［19］.那么，是否可以采用光滑非线性函数基于光滑双翅膀混沌系统构造光滑多翅膀混沌系统？本文将给出明确的答案.

自 1980 年，Shimizu 和 Morioka［22］提出双翅膀S-M混沌系统以来，目前鲜有文献报道基于双翅膀S-M混沌系统构造光滑多翅膀S-M混沌系统问题.需要注意的是：双翅膀S-M混沌系统是光滑系统；本文采用的代数函数是光滑非线性函数；本文构造的新单方向多翅膀S-M混沌系统和新二方向网格多翅膀S-M混沌系统都是光滑系统.

本文首先以双翅膀S-M混沌系统为基础，基于代数函数提出了两个新多分段非线性函数fN(x)和fM(z).然后，通过采用非线性函数fN(x)代替双翅膀S-M混沌系统中的平方项，构造出新单方向多翅膀S-M混沌系统.通过采用多分段非线性函数fM(z)代替新单方向多翅膀S-M混沌系统中的状态变量z，构造出新二方向网格多翅膀S-M混沌系统.随后，分析了新单方向多翅膀S-M混沌系统和新二方向网格多翅膀S-M混沌系统的非线性动力学行为，并得到了新单方向多翅膀S-M混沌吸引子和新二方向网格多翅膀S-M混沌吸引子的产生机理.其产生机理为指标2鞍焦平衡点用于产生翅膀.同时，对上述系统进行了电路实现.

1 单方向多翅膀S-M混沌系统的构造

首先引入代数函数，如式（1）所示

随着参数值d的变化，g（x）∈［-1，1］.当d=1时，代数函数g(x)变为具体的代数函数［23］.图1表示参数d取不同值时代数函数g(x)的曲线.基于代数函数g(x)，构造多分段非线性函数fN(x)，可表示为

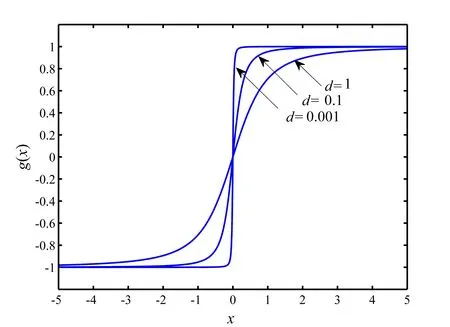
图1 代数函数g(x)的曲线Fig.1 Algebraic functiong(x)

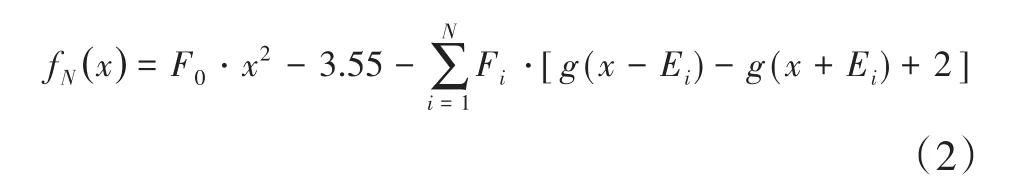
其中，F0=2，Fi=2 ⋅Ei，Ei=i+1.2，i=1，2，...，N（N<4），N为正整数.g(⋅)由式（1）定义，其中d=0.001.经典双翅膀S-M混沌系统［11］可表示为

其中，a=0.75，b=0.45是参数.x，y和z是状态变量.

为了构造单方向多翅膀S-M混沌系统，用多分段非线性函数fN(x)代替双翅膀S-M混沌系统（3）中的x2项，可得单方向多翅膀S-M混沌系统（4）.

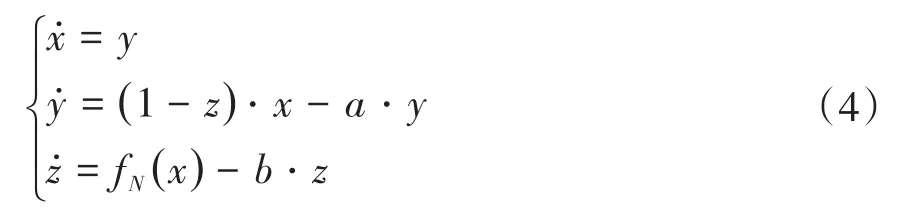
单方向多翅膀S-M混沌系统（4）可以产生4翅膀SM混沌吸引子，6翅膀S-M混沌吸引子和8翅膀SM 混沌吸引子 .当初值为 (1，1，1)，仿真时间为1000 s，4翅膀S-M混沌吸引子在x-z平面的相图如图2所示.4翅膀S-M混沌吸引子的Multisim电路实现结果如图3所示.对比图2和图3可知，电路实现结果与数值仿真结果一致.其他单方向多翅膀S-M混沌吸引子的电路实现结果也与对应的数值仿真结果一致，这里不再给出.

图2 4翅膀S-M混沌吸引子在x-z平面的相图Fig.2 Phase diagrams of the 4-wing S-M chaotic attractor in the x-z plane

图3 4翅膀S-M混沌吸引子的电路实现Fig.3 Circuit implementation of the 4-wing S-M chaotic attractor

2 单方向多翅膀S-M混沌系统的非线性动力学行为分析

2.1 单方向多翅膀S-M混沌吸引子的平衡点

为了研究单方向多翅膀S-M混沌吸引子的产生机理，对平衡点Q±n(x±n，y±n，z±n)进行分析 .令此混沌系统（4）中的ẋ=ẏ=ż=0，可得

由式（5）可得

根据式（6）可得单方向多翅膀S-M混沌系统（4）的平衡点Q±n(x±n，y±n，z±n)，n=0，1，2，...，N.图 4 表示当N=2时的多分段非线性函数fN(x).可以看到在x轴方向上有6个交点（x±0，x±1和x±2），在图中用‘·’表示.这6个交点可产生6个翅膀.

图4 当N=2时，多分段非线性函数fN(x)Fig.4 Multisegment nonlinear functionfN(x)withN=2

6 翅膀 S-M 混沌吸引子的平衡点Q±n（x±n，y±n，z±n）和特征值λ，如表1所示.由表1可知，特征值λ有一个负实根和一对实部为正的共轭复根.这表明平衡点（Q±0，Q±1和Q±2）为指标2［9］鞍焦平衡点.每个指标2鞍焦平衡点可产生一个相对应的翅膀，因此6个指标2鞍焦平衡点可产生6个翅膀.

表1 6翅膀S-M混沌吸引子的平衡点Q±n(x±n,y±n,z±n)和特征值λTable 1 EquilibriumQ±n(x±n,y±n,z±n)and eigenvalues λ of the 6-wing S-M chaotic attractor

2.2 单方向多翅膀S-M混沌吸引子的不变性和耗散性

单方向多翅膀S-M混沌系统（4）在(x，y，z)→(-x，-y，z)的变换下保持不变，即单方向多翅膀S-M混沌系统（4）关于z轴对称.通过体积的散度来计算单方向多翅膀 S-M 混沌系统（4）的耗散性，即

因此，单方向多翅膀S-M混沌系统（4）是耗散的.

2.3 单方向多翅膀S-M混沌吸引子的李亚普诺夫指数、分维数和庞加莱截面

本节以6翅膀S-M混沌吸引子为例来研究李亚普诺夫指数、分维数和庞加莱截面.当初值为(1，1，1)，仿真时间为3000 s，6翅膀S-M混沌吸引子的李亚普诺夫指数如图5所示.该图中有一个正的指数LE1，这表明单方向多翅膀S-M混沌系统（4）是混沌的.由LE1=0.348291，LE2=0.002137和LE3=-1.550427，可计算分维数［9］DL=2.226020.可知分维数是介于2和3之间的一个分数值，这表明单方向多翅膀S-M混沌系统（4）是混沌的.

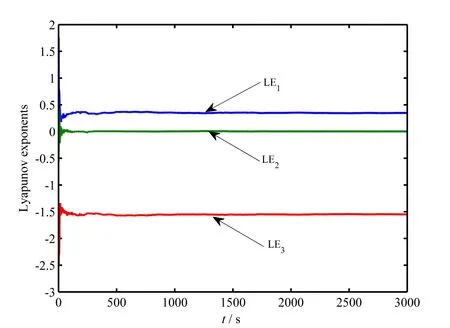
图5 6翅膀S-M混沌吸引子的李亚普诺夫指数Fig.5 Lyapunov exponents of the 6-wing S-M chaotic attractor

由图6可知，6翅膀S-M混沌吸引子的庞加莱截面由成片密集点组成，这表明单方向多翅膀S-M混沌系统（4）是混沌的.

图6 6翅膀S-M混沌吸引子的庞加莱截面Fig.6 Poincaré section of the 6-wing S-M chaotic attractor

3 二方向网格多翅膀S-M混沌系统的构造

本节利用代数函数g(x)构造多分段非线性函数fM(z)，并利用多分段非线性函数fM(z)构造二方向网格多翅膀S-M混沌系统.此系统能产生二方向网格多翅膀S-M混沌吸引子.利用代数函数g(x)构造多分段非线性函数fM(z)，其可以表示为

其中，G0=1.5，Ui=2iG0，i=1，2，...，M（M<2），M为整数.g(⋅)由式（1）定义，其中d=0.001.用多分段非线性函数fM(z)代替单方向多翅膀S-M混沌系统（4）中的状态变量z，可得二方向网格多翅膀S-M混沌系统（9）.

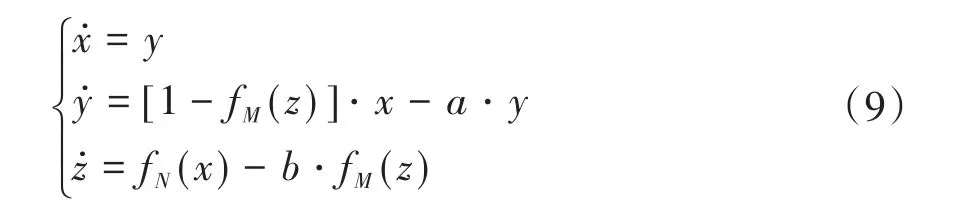
其中，a=0.75，b=0.45是系统参数.fN(x)和fM(z)分别由式（2）和式（8）定义.(2N+2)×(2M+2)网格多翅膀S-M混沌系统在x-z平面的相图如图7所示 .图 7（a），7（b）和 7（c）分别表示当 N=1，2，3，M=0时，4×2，6×2和8×2网格多翅膀S-M混沌吸引子的相图 .图7（d），7（e）和7（f）表示当N=1，2，3，M=1时，4× 4，6× 4和8× 4网格多翅膀S-M混沌吸引子的相图.

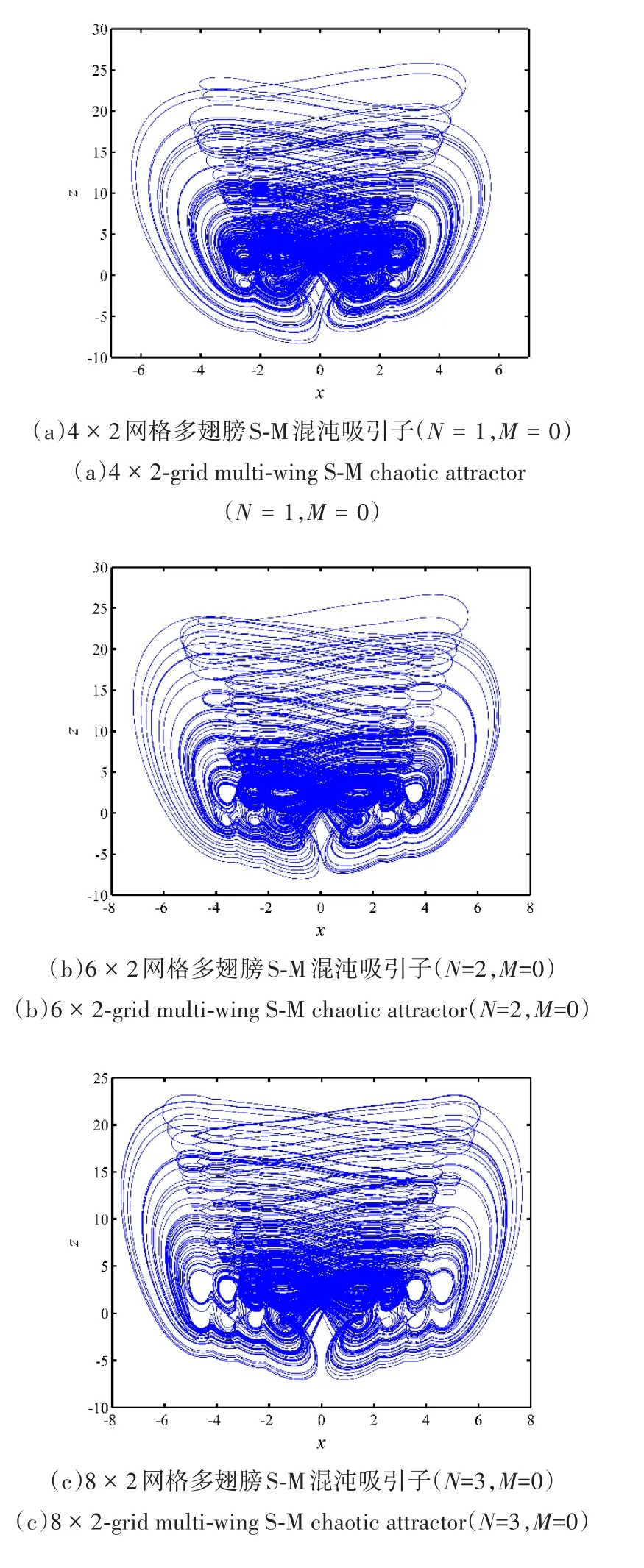
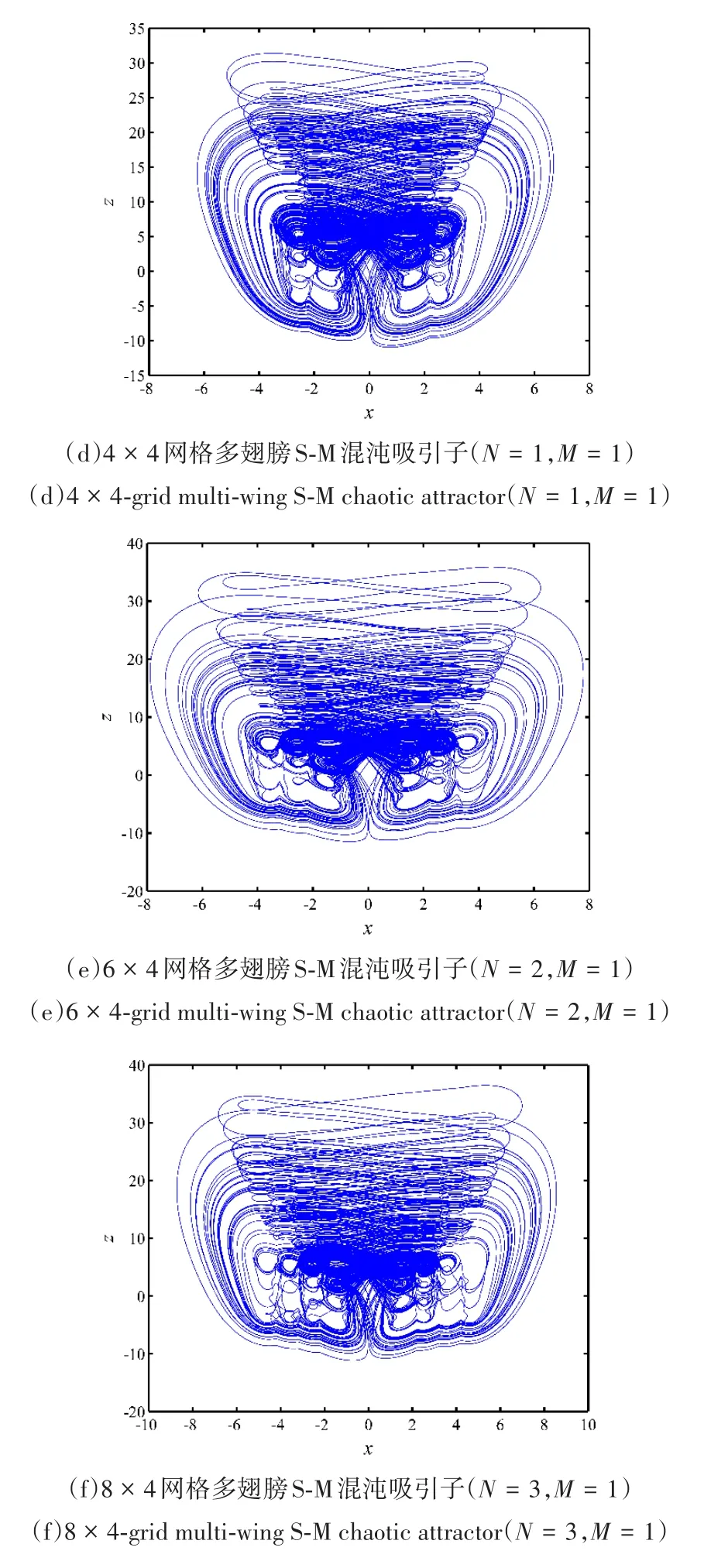
图7 (2N+2)×(2M+2)网格多翅膀S-M混沌吸引子在x-z平面的相图Fig.7 Phase diagrams of the(2N+2)×(2M+2)-grid multi-wing S-M chaotic attractors in the x-z plane

4×2网格多翅膀S-M混沌吸引子的Multisim电路实现结果如图8所示.对比图7（a）和图8可知，电路实现结果与数值仿真结果一致.其他二方向网格多翅膀S-M混沌吸引子的电路实现结果也与对应的数值仿真结果一致，这里不再给出.

图8 4×2网格多翅膀S-M混沌吸引子的电路实现Fig.8 Circuit implementation of the4×2-grid multi-wing S-M chaotic attractor

4 二方向网格多翅膀S-M混沌吸引子的非线性动力学行为分析

4.1 二方向网格多翅膀S-M混沌吸引子的平衡点、不变性和耗散性

本节通过分析平衡点 Q±n，±m(x±n，y±n，z±m)来研究二方向网格多翅膀S-M混沌系统的产生机理.令二方向网格多翅膀S-M混沌系统（9）中ẋ=ẏ==0，可得

由式（10）可得

由式（11）得到二方向网格多翅膀S-M混沌系统（9）的平衡点 Q±n，±m(x±n，y±n，z±m)，n=0，1，2，...，N，m=0，1，2，…M.图 9表示当 M=1时的多分段非线性函数fM(z).可以看到在z轴方向上有4个交点（z±0和z±1），在图中用‘·’表示.这4个交点可产生4个翅膀.

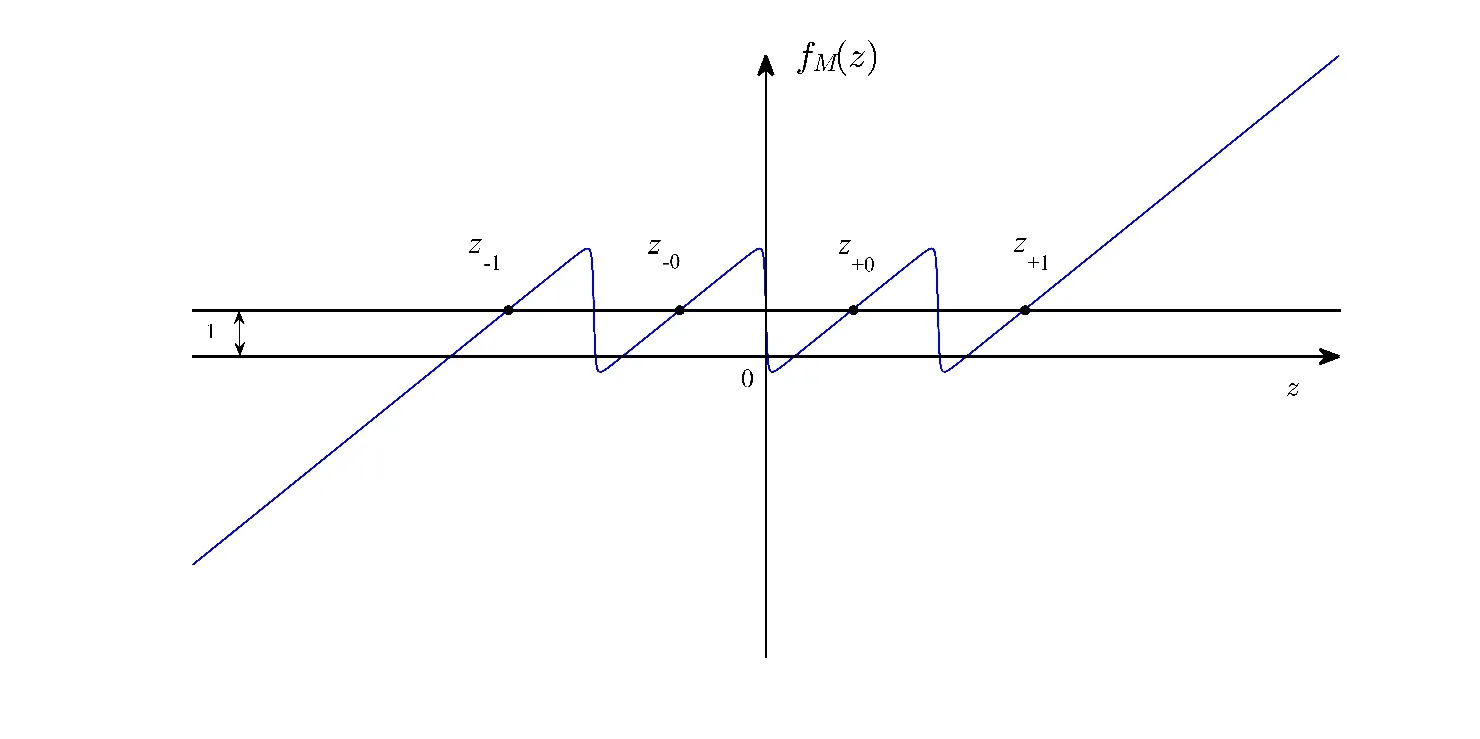
图9 当M=1时，多分段非线性函数fM(z)Fig.9 Multisegment nonlinear functionfM(z)withM=1

6×4网格多翅膀S-M混沌吸引子的平衡点Q±n，±m(x±n，y±n，z±m)和特征值 λ，如表 2 所示 .由表 2可知，特征值λ有一个负实根和一对实部为正的共轭复根 .这表明平衡点（Q±0，±0，Q±1，±0，Q±2，±0，Q±0，±1，Q±1，±1，Q±2，±1）为指标 2［9］鞍焦平衡点 .每个指标 2鞍焦平衡点可产生一个相对应的翅膀，因此24个指标2鞍焦平衡点可产生24个翅膀.

表2 6×4网格多翅膀S-M混沌吸引子的平衡点Q±n,±m(x±n,y±n,z±m)和特征值λTable 2 EquilibriumQ±n,± m(x±n,y±n,z±m)and eigenvalues λ of the6×4-grid multi-wing S-M chaotic attractor

二方向网格多翅膀S-M混沌系统（9）的不变性和耗散性计算方法与单方向多翅膀S-M混沌系统（4）相同，这里不再详细讨论.

4.2 二方向网格多翅膀S-M混沌吸引子的李亚普诺夫指数、分维数和庞加莱截面

本节以6×4网格多翅膀S-M混沌吸引子为例来分析李亚普诺夫指数、分维数和庞加莱截面.当初值为(1，1，1)，仿真时间为3000 s，6 × 4网格多翅膀S-M混沌系统的李亚普诺夫指数如图10所示.该图中显然存在一个正的李亚普诺夫指数LE1，这表明二方向网格多翅膀S-M混沌系统（9）是混沌的 .由 LE1=0.453331，LE2=-0.020405和 LE3=-1.567040，可计算分维数［9］DL=2.276269.可知分维数是介于2和3之间的一个分数值，这表明二方向网格多翅膀S-M混沌系统（9）是混沌的.

图10 6×4网格多翅膀S-M混沌吸引子的李亚普诺夫指数Fig.10 Lyapunov exponents of the 6×4-grid multi-wing S-M chaotic attractor

由图11可知，6×4网格多翅膀S-M混沌吸引子的庞加莱截面是由成片的密集点构成，这表明二方向网格多翅膀S-M混沌系统（9）是混沌的.

图11 6×4网格多翅膀S-M混沌吸引子的庞加莱截面Fig.11 Poincaré section of the6 × 4-grid multi-wing S-M chaotic attractor

5 动力学行为演变方向及复杂度分析

以6翅膀S-M混沌系统（a=0.75，b∈[0，2]）为例，分析李亚普诺夫指数如图12所示及分岔图如图13所示.从图12-图13可知，随着参数b的变化，6翅膀S-M混沌系统由混沌态（0≤b<1）演变为周期态（1≤b≤2）.

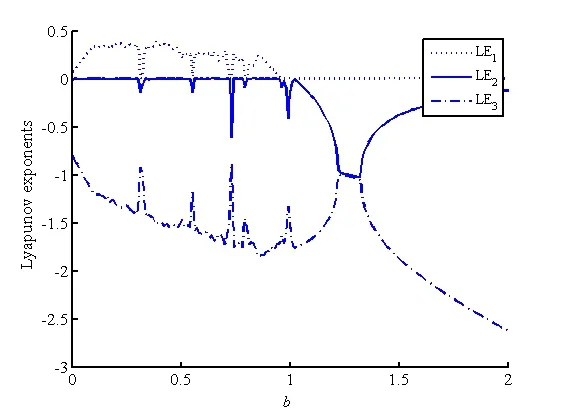
图12 随参数b变化的李亚普诺夫指数Fig.12 Lyapunov exponents with varying parameterb

图13 分岔图Fig.13 Bifurcation diagram

对经典双翅膀S-M混沌系统（3）、单方向多翅膀S-M混沌系统（4）以及二方向网格多翅膀S-M混沌系统（9），分别从SE复杂度［24］的最大值和平均值进行比较分析，结果如表3所示.由表3可知，对于二方向网格多翅膀S-M混沌系统（9），SE复杂度的平均值比经典双翅膀S-M混沌系统（3）、单方向多翅膀S-M混沌系统（4）的大.对于单方向多翅膀S-M混沌系统（4），SE复杂度的最大值和平均值比经典双翅膀S-M混沌系统（3）的大.由此可知对经典双翅膀S-M混沌系统（3）多翅膀化后，所得单方向多翅膀S-M混沌系统（4）以及二方向网格多翅膀S-M混沌系统（9）复杂度增加.需要注意的是，复杂度特性对比研究中，单方向多翅膀S-M混沌系统（4）以 6翅 膀 S-M 混 沌系 统（a=0.75，b∈[0，2]）为例，二方向网格多翅膀S-M混沌系统（9）以6×4网格多翅膀S-M混沌系统（a=0.75，b∈ [0，2]）为例.

表3 S-M混沌系统(3)，(4)，(9)复杂度特性对比Table 3 Comparison of complexity characteristics of S-M chaotic systems(3),(4),(9)

6 结论

本文基于光滑代数函数构造了两个新光滑多分段非线性函数fN(x)和fM(z).然后，采用这两个新光滑多分段非线性函数构造了新光滑单方向多翅膀S-M混沌系统和新光滑二方向网格多翅膀S-M混沌系统.翅膀的个数由指标2鞍焦平衡点的个数来确定.需要说明的是，该光滑代数函数也可以被用于构造其他新光滑多分段非线性函数.此外，本文构造的新光滑单方向多翅膀S-M混沌系统和新光滑二方向网格多翅膀S-M混沌系统可应用于保密通信，图像加密等领域.