隋广宇 , 李正光, 吴柏生

(1. 吉林大学 数学学院, 长春 130012; 2. 广东工业大学 机电工程学院, 广州 510006)

0 引 言

在航空、 航天、 机械、 建筑等许多工程领域, 结构的固有频率和模态振型关于设计变量或系统参数的导数信息, 即结构特征灵敏度分析, 是CAE(computer aided engineering)分析的重要组成部分, 常用于求解结构优化设计、 模型修改、 系统控制和损伤探测等工程问题[1]. 目前, 已有多种计算特征灵敏度的分析方法, 如有限差分法、 模态法、 代数法、 迭代法和Nelson类方法等[2-3].

相对于无阻尼结构, 阻尼结构更复杂且更能真实模拟现实结构, 其特征灵敏度分析也更有实际意义. 阻尼结构的模态振型和频率满足二次特征值问题：

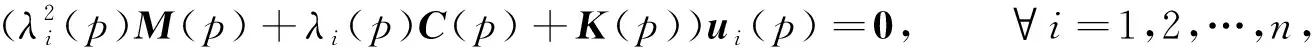
(1)

其中p为设计变量,M(p),K(p),C(p)是p的实对称矩阵函数, 分别为质量矩阵、 刚度矩阵和阻尼矩阵,n为系统自由度个数,ui为模态振型,λi为特征值.由于阻尼C(p)的存在, 因此特征值和模态振型是复数形式的.ω=Im(λi)/(2π)为阻尼圆频率.对问题(1)进行灵敏度分析, 主要有两种策略： 第一种策略是引入状态空间, 将原二次特征问题线性化, 转换为状态空间的一般广义特征值问题, 然后利用广义特征值灵敏度分析方法进行求解[4], 但由于引入了状态空间, 使问题的求解规模变为2n, 增大了问题的求解复杂度; 第二种策略是直接在n维空间进行求解.Adhikari[5-6]分别根据状态空间中的模态振型与频率关系和无阻尼模态的性质给出了n维空间上计算特征灵敏度的模态展开法; Li等[7]通过对模态法应用Neumann级数展开技术减小了模态截断的影响； Lee等[8]和Choi等[9]通过扩展无阻尼结构特征灵敏度分析中的代数方法, 利用加边形式构造出了模态灵敏度求解方程； Xie[10]提出了一种同时迭代方法求解阻尼结构特征灵敏度. 上述方法都是针对孤立阻尼频率的情形, 对于重频情形, Wang等[11-12]扩展了单频情形下的特解求解方法, 给出了加边形式及其改进的特解求解方程, 但由于加边的存在改变了原有矩阵的稀疏性, 增加了存储和计算困难; Li等[13]采用组合正则条件的方法给出一种特解求解方法, 但特解方程的建立同样采取了加边形式.

Nelson方法[14]最初是针对标准特征值问题的孤立特征值灵敏度分析提出的, 其优点是求解仅需所关心的频率和模态振型信息, 不需要对矩阵行列进行重排, 保持了原有矩阵的稀疏性. Cardani等[15]和Friswell等[16]扩展了Nelson方法用于求解阻尼结构的特征灵敏度分析, 但只适用于单频问题； Ojalvo[17]和Dailey[18]发展了Nelson方法求解对称广义重特征值的特征灵敏度分析问题； Guedria等[19]发展了Nelson方法用于求解特征二阶导数问题； Wu等[20]改进了Nelson方法, 给出了一种构造特解求解方程的方法, 用于求解重频特征灵敏度问题, 但其只适用于无阻尼系统.

针对阻尼结构重频复模态灵敏度计算问题, 本文提出一种新的扩展Nelson方法. 通过构造新的灵敏度特解控制方程, 并证明其系数矩阵的非奇异性, 扩展了Nelson方法, 使其可以求解计算结构重频复模态灵敏度问题. 本文方法仅需利用重频频率对应的模态振型, 无需扩大方程求解规模和矩阵重排. 数值实例显示了该方法的有效性.

1 扩展Nelson方法

假设阻尼振动系统(1)在设计点p0存在m重频率, 不妨令λi+1(p0)=λi+2(p0)=…=λi+m(p0)=λ,u1(p0),u2(p0),…,um(p0)是对应的线性无关模态振型.相应的二次特征值问题可以写成矩阵形式：

M(p)U(p)Λ2(p)+C(p)U(p)Λ(p)+K(p)U(p)=0,

(2)

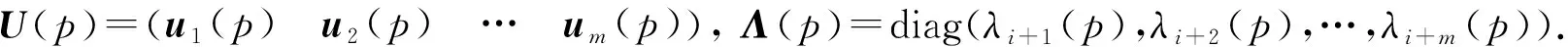
为保证特征向量的唯一性, 通常用下列正则条件：

UT(p)(2λ(p)M(p)+C(p))U(p)=Im,

(3)

其中Im是m阶单位矩阵.显然u1(p0),u2(p0),…,um(p0)的任意线性组合也是其特征向量, 并且一般情况下u1(p0),u2(p0),…,um(p0)不一定是可导的特征向量.记在p0处λi+1(p0)=λi+2(p0)=…=λi+m(p0)=λ的相应可导特征向量为Z, 则有Z=UΓ, 其中Γ为m×m阶正交矩阵.对可导的二次特征值问题：

M(p)Z(p)Λ2(p)+C(p)Z(p)Λ(p)+K(p)Z(p)=0,

(4)

关于设计变量p在p0点求导得

FZ′=G,

(5)

这里

F=λ2M+λC+K,G=-(2λM+C)ZΛ′-(λ2M′+λC′+K′)Z.

为书写方便, 省略上述式中各矩阵函数p的表示, 有( )′表示p0处的导数.对式(5)两边左乘UT并利用正则条件(3), 可得

EΓ=ΓΛ′,

(6)

其中E=-UT(λ2M′+λC′+K′)U.式(6)为m×m阶标准特征值问题, 求解可得Γ和Λ′, 继而得到可导特征向量Z.这里假设Λ′的各元素互异, 当Λ′有重根时, 需要考虑高阶导数信息.

方程(5)是一个秩为n-m的奇异方程, 不能直接求解得到Z′, 本文扩展Nelson方法, 将方程的解即特征向量导数表示为通解加特解形式, 即

Z′=V+Zc,

(7)

这里V是特解.特解V也满足方程(5), 下面求该特解.将式(4)写成如下形式：

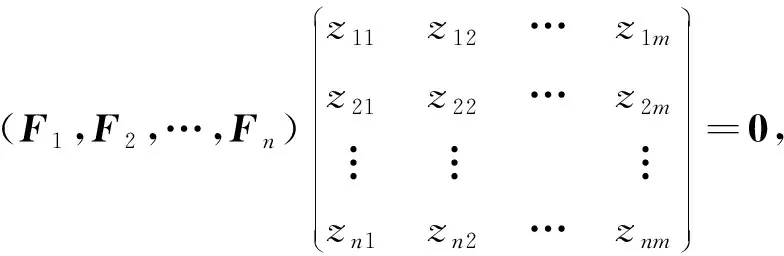
(8)

其中Fj(j=1,2,…,n)表示矩阵F的第j列.因为矩阵F的秩是n-m, 特征向量矩阵Z的秩是m, 所以可从Z中选择m行得到一个m阶的子块Zm,m, 并使该子块的行列式非零.不失一般性, 假设Z的前m行满足上述条件, 即

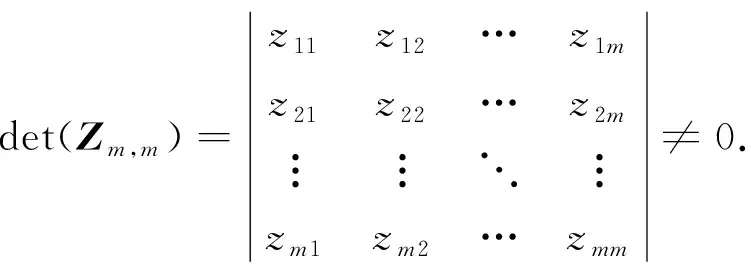
(9)

则式(8)可写成下列形式：

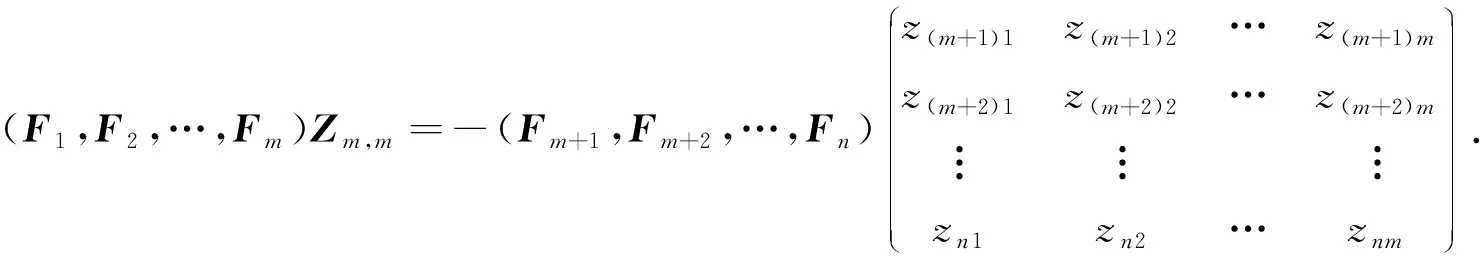
(10)

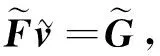
(11)

将ZT左乘方程(5)两端得到ZTG=0, 进而有

ZT(FV-G)=0.

(12)

将式(12)写成分块形式:

(13)

展开式(13)有

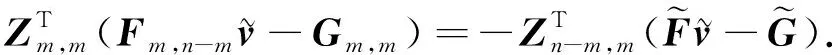
(14)

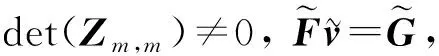
(15)

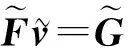
在实际计算特解V时, 不需要将矩阵F删去某些行列及重排, 只需根据Z选出一些行列, 将这些行列的非对角线元素设为零, 对角线元素不变即可, 这样可以获得较好的条件数.相应地, 将G的对应行元素设为零即可.

对方程(5)关于设计变量p求导, 有

将式(16)两边同时左乘ZT可得

将Z′=V+Zc代入式(17), 由规范化条件ZT(2λM+C)Z=Im得

对比式(18)两边, 当i≠j时, 有

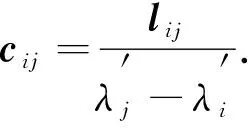
(19)

当i=j时, 对规范化条件ZT(2λM+C)Z=Im求导, 代入Z′=V+Zc并应用ZT(2λM+C)Z=Im, 得矩阵c的对角元为

cii=-0.5[ZT(2λM′+C′)Z-ZT(2λM+C)V-VT(2λM+C)Z]-ZTMZΛ′.

(20)

从而得到了系数矩阵c的所有元素, 将特解V与通解系数矩阵c代入式(7)即可得模态灵敏度Z′.

扩展的Nelson方法求解阻尼结构特征灵敏度分析步骤如下：

1) 求解方程(6), 由已知的特征模态计算可导的特征模态和特征值导数；

2) 从可导的特征向量矩阵Z中选择一个m阶的非奇异矩阵, 记录所选择的行数lj(j=1,2,…,m);

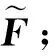
6) 利用式(19),(20)得到矩阵c；

7) 利用式(7)得到模态振型灵敏度Z′.

2 数值实验

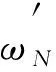
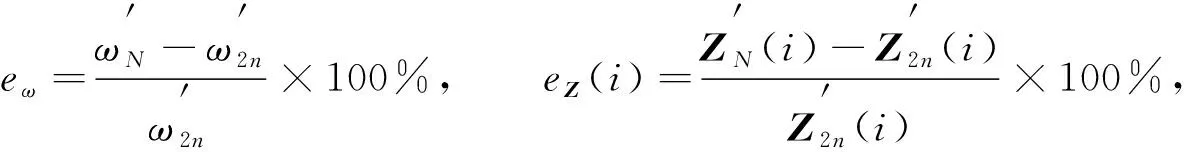
其中Z(i)表示向量Z的第i个分量.采用模态置信准则[21]

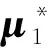
例1考虑如图1所示带有黏性阻尼的质量弹簧系统, 其中k=1 000 N/m,m=1 kg,c=10 N·s/m,k1=1 000 N/m. 系统的质量矩阵M、 刚度矩阵K和阻尼矩阵C分别为

将刚度k作为设计参数p, 在p0=1 000 N/m点系统矩阵的导数分别为

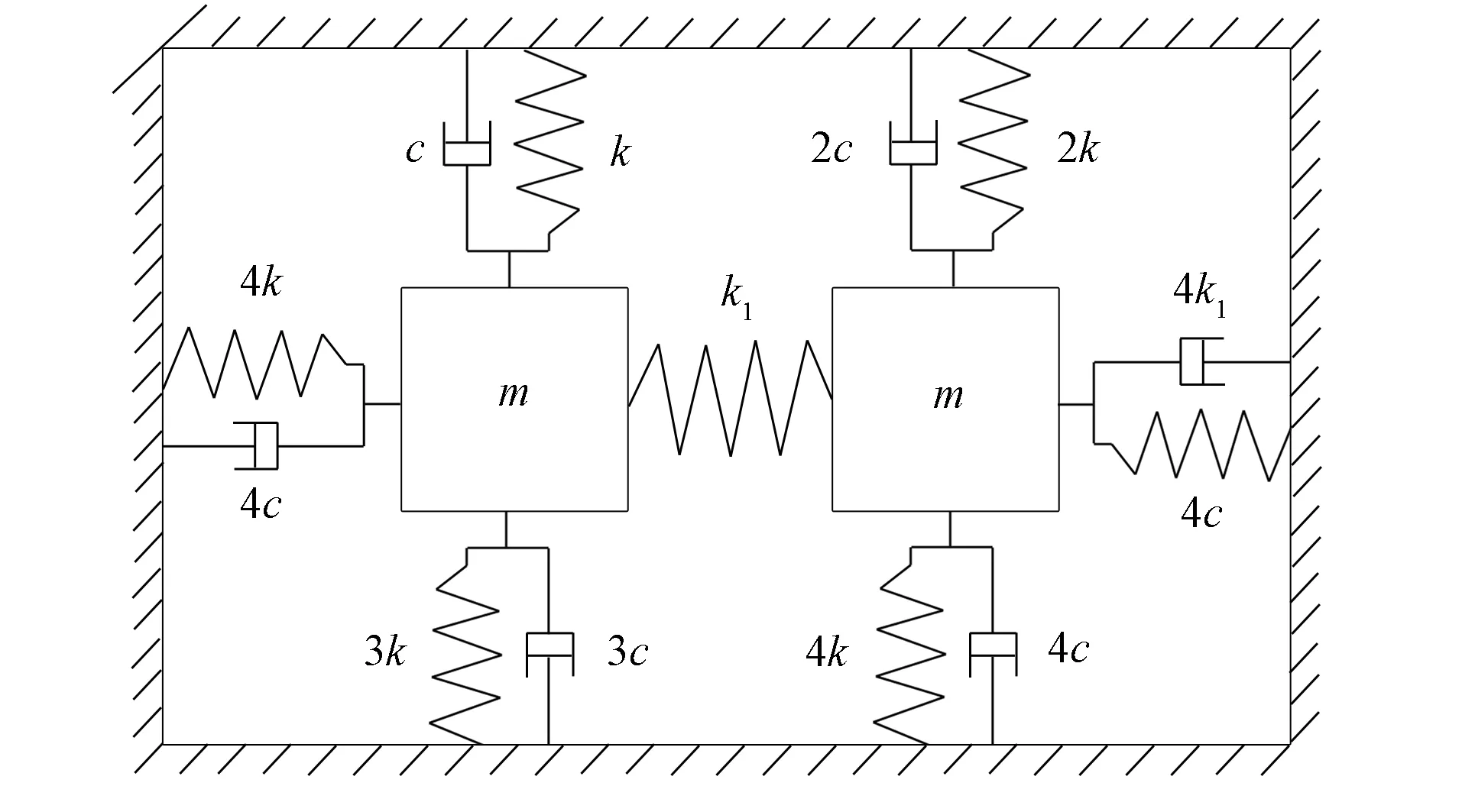
图1 质量弹簧阻尼系统Fig.1 Mass spring damped system

该系统有一个复重特征值

λ=-20.000 0+60.000 0i,

对应的系统阻尼圆频率ω=9.549 3 rad/s. 使用本文方法和2n空间线性化方法得到的频率灵敏度列于表1, 两个可导的模态及模态灵敏度分别列于表2和表3. 由表1～表3可见, 本文方法求解得到的频率灵敏度误差在计算机精度下达到0, 而模态振型灵敏度的各分量误差也达10-13量级. 本文方法计算得到两个可导模态振型的灵敏度与2n空间线性化方法得到的模态振型灵敏度MAC值均为1.0. 结果表明, 本文方法计算精度较高.

表1 质量弹簧阻尼系统频率灵敏度比较

表2 质量弹簧阻尼系统可导模态振型1及其灵敏度比较

表3 质量弹簧阻尼系统可导模态振型2及其灵敏度比较

例2考虑如图2所示的由相同微结构组成的一个平面桁架系统, 该系统每个局部结构均可视为由弹簧阻尼结构组成, 其材料特性为： 材料密度ρ=7.8×103kg/m3, 弹性模量E=2.1×1011Pa, 阻尼系数c=100 N·s/m, 杆的截面积为A=0.1 m2.

考虑如图3所示深色部分杆件的截面积为设计变量, 考虑其在A0=0.1 m2的圆频率及模态振型灵敏度. 该结构有一个重特征值λ=-2.258 1×10-4+3.672 5×102i, 对应的圆频率为58.449 9 rad/s. 使用本文方法和线性化策略计算圆频率及图2所示黑点处x方向自由度模态分量灵敏度, 结果列于表4～表6.由表4～表6可见, 本文方法求解得到的频率灵敏度误差在计算机精度下达10-8, 而特征模态振型灵敏度分量的误差达10-6量级.本文方法计算得到两个可导模态振型的灵敏度与2n空间线性化方法得到的模态振型灵敏度MAC值均为1.0. 结果表明, 本文方法计算精度较高. 本文方法的计算时间是0.015 2 s, 2n空间线性化方法的计算时间是0.0757 s, 本文方法的计算效率约为线性化方法的5倍.

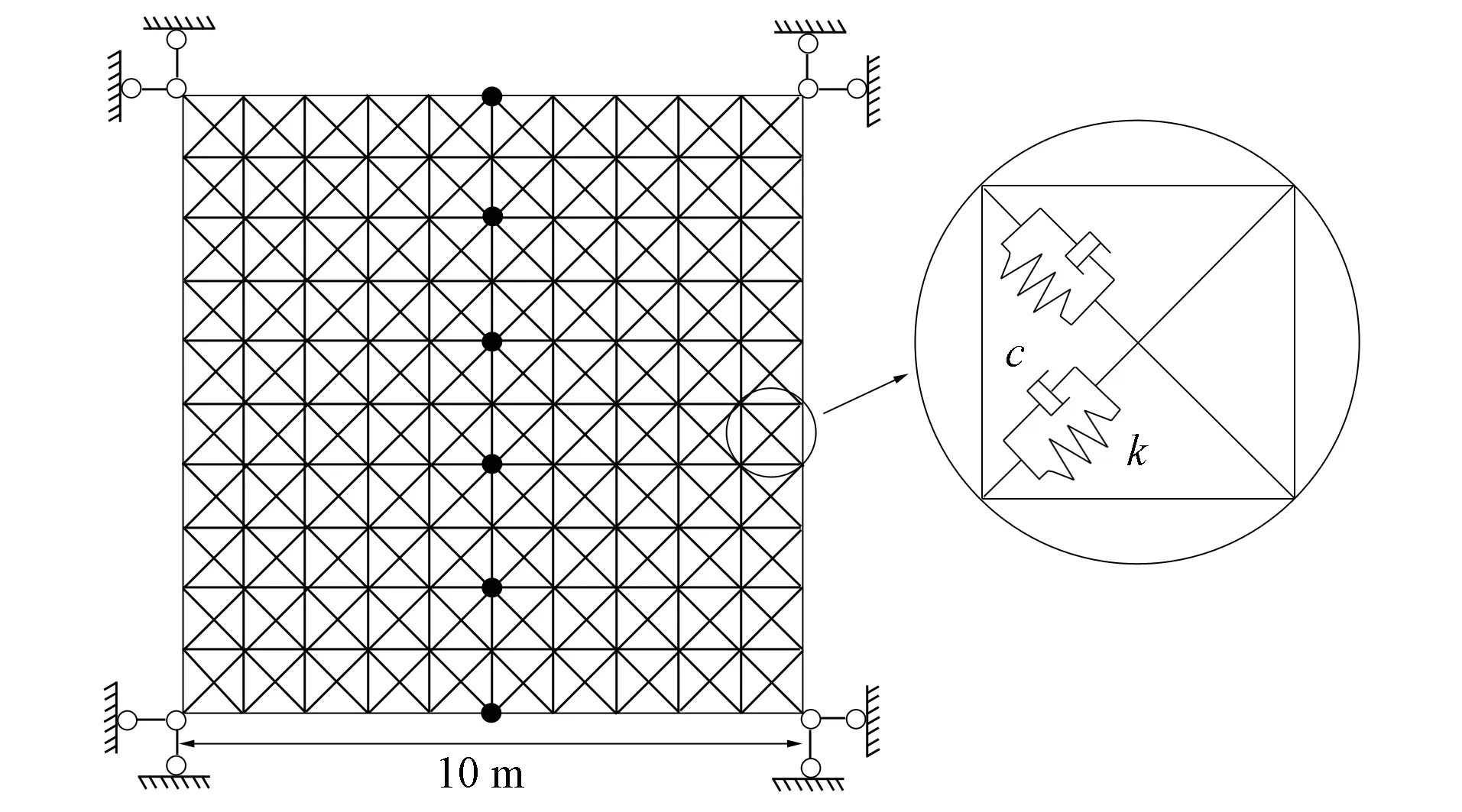
图2 平面桁架结构Fig.2 Plane truss structure

图3 桁架结构设计变量Fig.3 Design variables of truss structure

表4 平面桁架系统频率灵敏度比较

表5 平面桁架系统可导模态振型1及其灵敏度比较

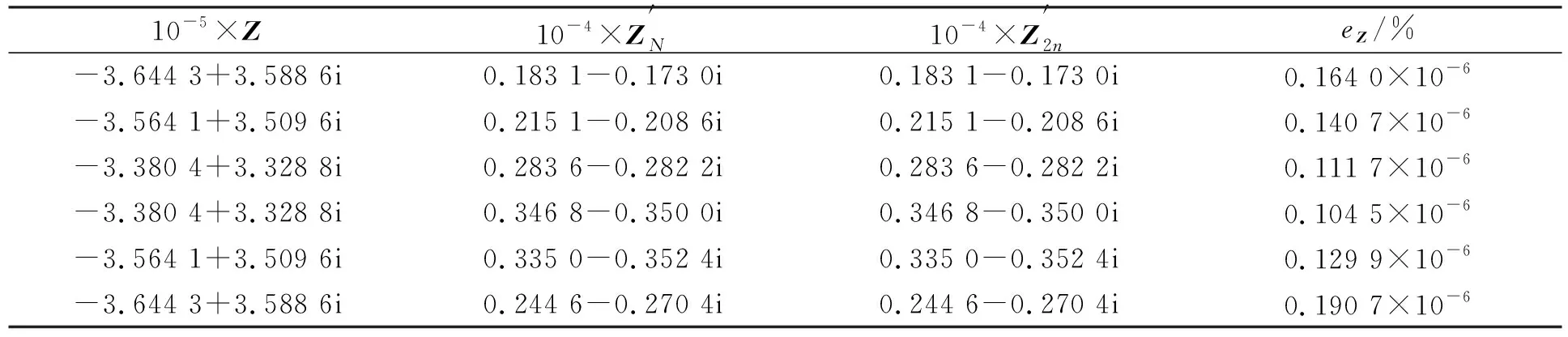
表6 平面桁架系统可导模态振型2及其灵敏度比较

综上所述, 针对阻尼结构重频复模态灵敏度计算问题, 本文提出了一种新的扩展Nelson方法, 通过构造新的灵敏度特解控制方程, 并证明其系数矩阵的非奇异性, 使其可以计算结构重频复模态振型灵敏度. 本文方法仅需利用重频频率对应的模态振型, 无需扩大方程求解规模和矩阵重排, 数值实例验证了本文方法的有效性.