王松华, 夏 师, 黎 勇

(百色学院 数学与统计学院, 广西 百色533000)

0 引 言

考虑如下无约束优化问题：

min{f(x)|x∈n},

(1)

其中：f:n→二次连续可微.非线性共轭梯度法是求解大规模无约束优化问题的一类重要方法, 其迭代公式为

xk+1=xk+αkdk,

(2)

d0=-g0,dk=-gk+βkdk-1,k≥1,

(3)

式中αk为步长因子,dk为搜索方向,gk为梯度函数f(xk)的简记,βk为共轭参数.经典的共轭梯度法有FR(Fletcher-Reeves),PRP(Polak-Ribière-Polyak),HS(Hestenes-Stiefel),CD(Conjugate-Descent),DY(Dai-Yuan)和LS(Liu-Storey)算法等[1]. 研究表明,类共轭参数公式的分子为‖gk‖2(‖‖为欧氏范数), 这类算法在弱Wolfe-Powell线搜索条件下对一般函数全局收敛, 但数值结果并不理想； 而类共轭参数公式的分子为这类算法具有自动重开始的性能, 可有效避免连续产生小步长, 数值结果较好, 但在弱Wolfe-Powell线搜索下算法的下降性不能保证.

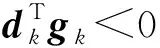
(4)

基于充分下降性的条件, Hager等[6]在自调比BFGS方法(拟牛顿法)的基础上提出了一种修正HS共轭梯度法, 称为HZ(Hager-Zhang)共轭梯度法, 其共轭参数公式为

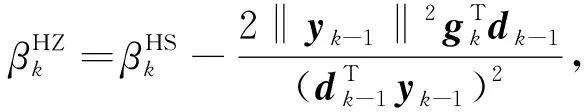
(5)

(6)

其中η>0.本文简称该方法为HZb算法. HZb算法具有稳定和有效的数值性能, 是目前数值结果性能最好的算法之一[7]. 之后, Hager等[8]又将HZ算法进行推广, 得到了与文献[2]方法完全相似的理论结果, 本文简称为HZp算法, 其共轭参数公式为

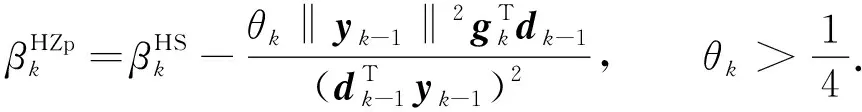
(7)

文献[9-13]基于搜索方向满足充分下降条件的理论方法, 给出了HZ算法的推广及应用.

文献[14-16]对线搜索型非线性共轭梯度法的研究表明, 搜索方向具有信赖域性质, 对算法的全局收敛性分析有积极作用, 即搜索方向满足下列条件：

‖dk‖≤c0‖gk‖, ∀k∈,c0>0.

(8)

文献[6,8-13]中的HZ算法及其推广算法均满足充分下降性条件, 但没有信赖域性质. Yuan等[16]研究了一类新型非凸函数的共轭梯度法簇, 构建了一组搜索方向公式自动满足条件(7),(8), 不仅有良好的收敛性质, 而且初步数值实验结果表明, 该算法比经典PRP,HS,CD,FR,LS和DY等算法性能更好. 文献[16]还给出了一种修正HZ搜索方向公式, 但未建立相应的算法. 受文献[6,8,14-16]工作的启发, 本文提出一类针对大规模无约束优化问题的修正HZ共轭梯度法, 并讨论新算法的全局收敛性和R-线性收敛速度, 给出其数值性能分析.

1 算法及其性质

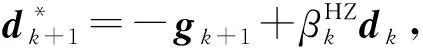
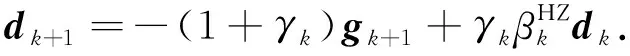
(9)

本文采用弱Wolfe-Powell线搜索[17], 并联合搜索方向式(9), 构建新的修正HZ算法, 简称为MHZ算法, 其步骤如下：

取初始点x0∈n, 常数令k∶=0.

1) 如果‖gk‖≤ε, 则停止;

2) 采用弱Wolfe-Powell(WWP)线搜索计算步长αk, WWP线搜索公式为

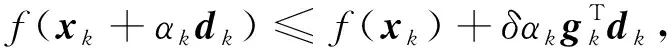
(10)

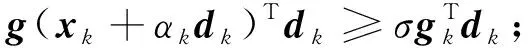
(11)

3) 计算xk+1=xk+αkdk;

4) 如果‖gk+1‖≤ε, 则停止;

6) 计算修改后的搜索方向

7) 令k=k+1, 返回步骤2).

引理1如果搜索方向由MHZ算法给出, 则下式成立：

(12)

证毕.

引理2如果搜索方向由MHZ算法给出, 则下式成立：

‖dk+1‖≤(1+ρ0)‖gk+1‖, 0<ρ0<1.

(13)

证明： 当k=0时, 式(13)显然成立.当k≥1时, 对式(9)两边取范数, 可得

证毕.

引理1表明, MHZ算法的搜索方向不依赖任何线搜索, 满足充分下降性; 引理2表明, MHZ算法的搜索方向具有信赖域性质.

2 MHZ算法收敛性分析

假设11) 目标函数f(x)二次连续可微, 有下界； 定义的水平集L0={x|f(x)≤f(x0)}有界.

2) 目标函数f(x)的梯度gk是Lipschitz连续的, 即存在常数L>0, 使得下式成立：

‖g(x)-g(y)‖≤L‖x-y‖, ∀x,y∈n.

(14)

结合引理1、 引理2和假设1, 下面证明MHZ算法是全局收敛的, 所用方法类似文献[16]中定理3.

定理1如果假设1成立, 序列{xk,dk,αk,gk}由MHZ算法给出, 则下式成立：

(15)

证明： 由式(10),(12), 可得

整理得

δαk(1-ρ0)‖gk‖2≤f(xk)-f(xk+1),

(16)

对不等式(16)从k=0到∞累加求和, 并结合假设1中1), 可得

即

αk‖gk‖2→0,k→∞.

(17)

由式(11),(13),(14), 可得

整理得

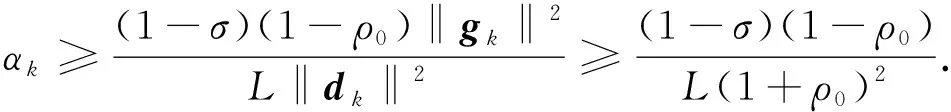
(18)

假设2若函数f(x)为二次连续可微一致凸函数, 则对∀x,d∈n, 存在SM≥sN>0, 使得下式成立:

sN‖d‖2≤dT2f(x)d≤SM‖d‖2,

假设1和假设2表明, 问题(1)存在唯一解x*, 对∀x∈n, 如下两个不等式成立：

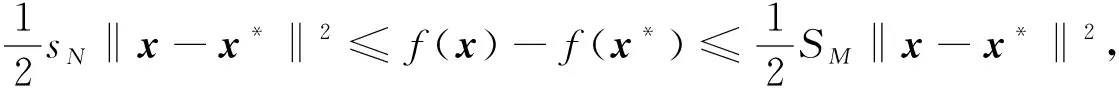
(19)

sN‖x-x*‖≤‖g(xk)‖≤SM‖x-x*‖.

(20)

定理2若假设2成立,x*是问题(1)的唯一解, 则存在常数a>0,l0∈(0,1), 使得下式成立:

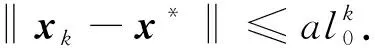
(21)

证明： 由式(4),(10), 再联合式(19),(20), 可得

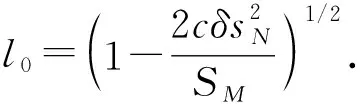
由式(19), 得

定理2表明, MHZ算法对一致凸函数具有R-线性收敛速度.

3 数值实验

为检验MHZ算法的有效性, 本文采用文献[18]的40个非线性函数进行数值实验, 函数名称列于表1. 将MHZ算法与HZ算法、 HZb算法、 HZp算法进行对比分析. 数值实验中, 对应的HZ算法、 HZb算法和HZp算法, 分别在MHZ算法中, 采用下式替换MHZ算法的步骤5)和步骤6)计算搜索方向dk+1, 其余步骤不变, 3类对比算法的搜索方向dk+1公式分别为

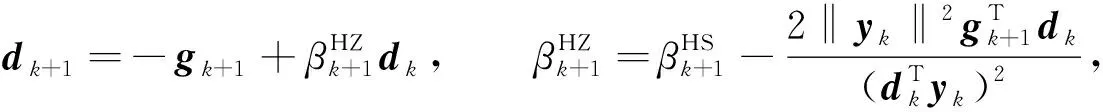
(23)

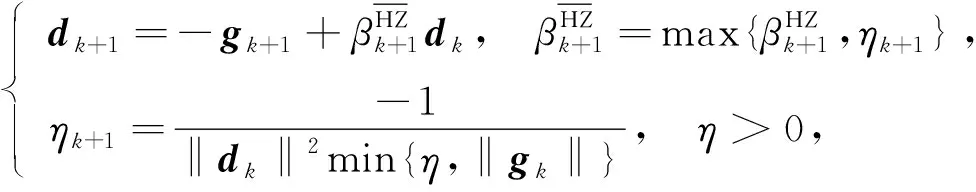
(24)

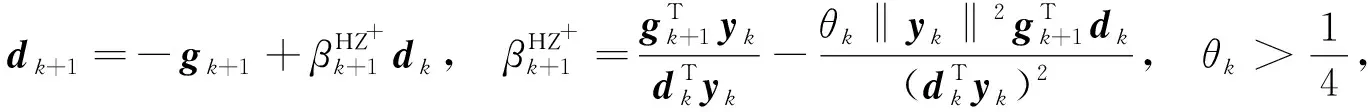
(25)

其中yk=gk+1-gk.

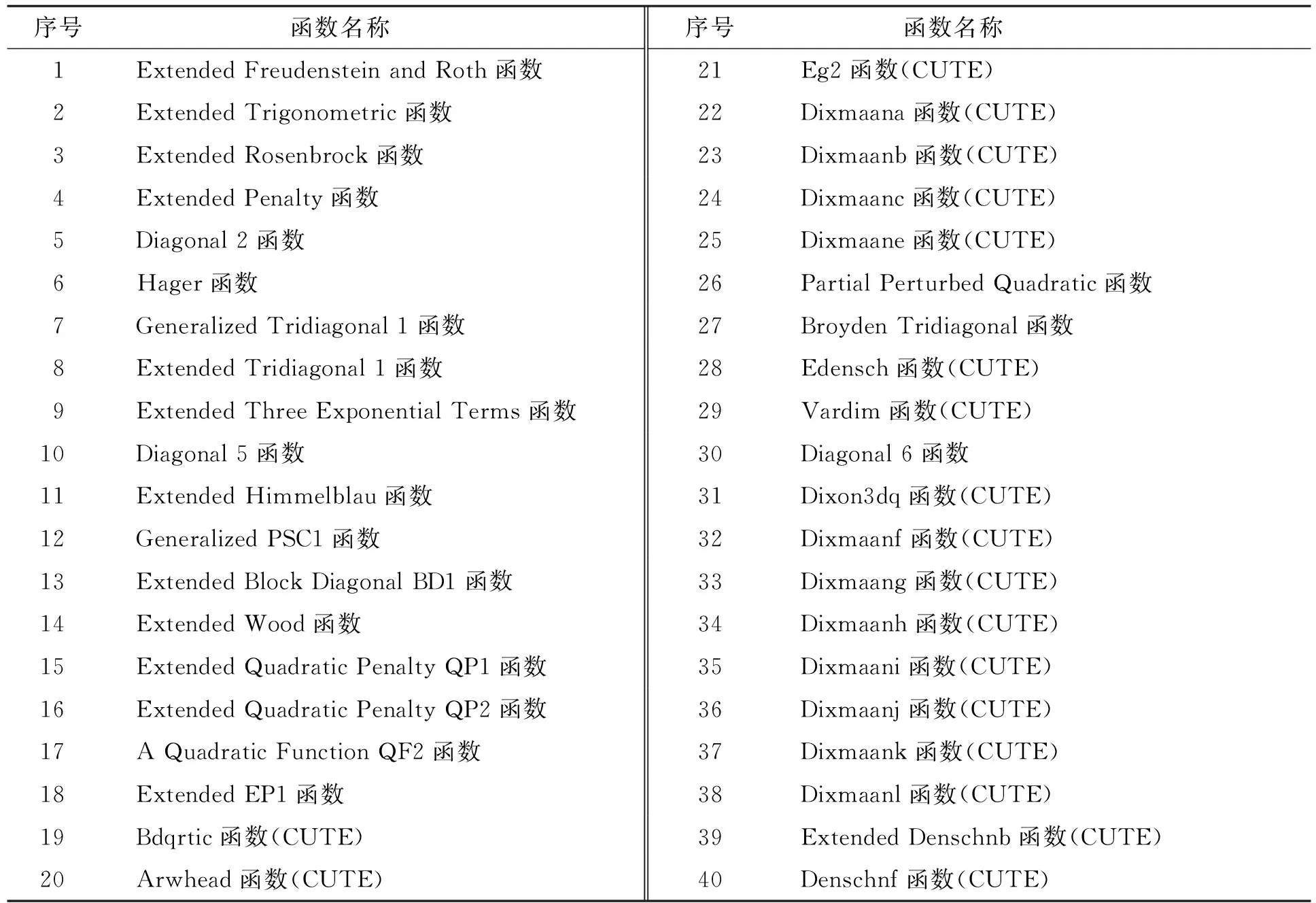
表1 测试函数名称

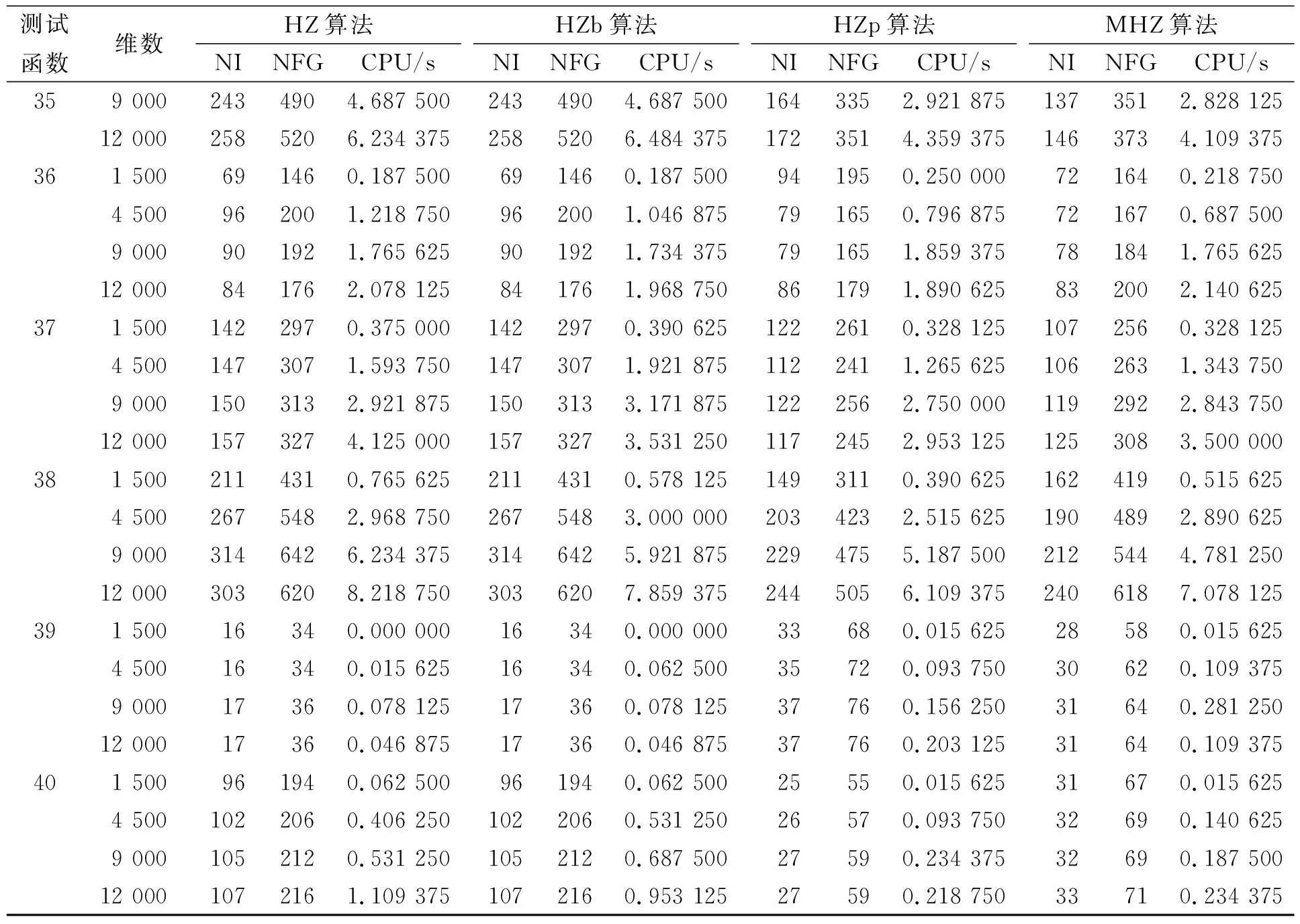
数值实验采用MATLAB编写程序并运行. 计算机配置： Windows 10操作系统, Intel(R)Xeon(R)CPU, E5507 @2.27 GHz, 内存4.00 GB； 终止条件： ‖gk‖≤10-6或者迭代次数NI<800； 4种算法相应的参数设置：δ=0.22,σ=0.93,ρ0=0.18,η=3,θ=1,ε=10-6； 维数为1 500,4 500,9 000,12 000； 主要针对4种算法的迭代次数NI、 函数值的计算次数NFG和实验运行所需时间CPU这3个常用指标进行测试. 4种算法的数值实验结果列于表2.

表2 4种算法的数值实验结果

续表2

续表2

续表2

由表2可见, 4种算法均能解决所给定的测试问题, MHZ算法比HZ算法、 HZb算法和HZp算法更有效. 下面采用Dolan等[19]的评价准则, 对4种算法进行综合性能评估. 该评价准则为： 曲线越靠上所对应的算法越稳定, 效果越好. 4种算法的迭代次数、函数值计算次数和CPU运行时间的性能评估结果如图1所示. 在计算精度一致的条件下, 由图1(A),(B)可见, MHZ算法最优, 其次为HZb算法和HZp算法, 这3种算法均比HZ算法好, 充分说明了这4类算法的性能发展趋势. 由图1(C)可见, 4种算法CPU运行时间较接近, MHZ算法总体结果较好, 这可能是因为本文实验相关参数的取值对CPU运行时间有一定影响.

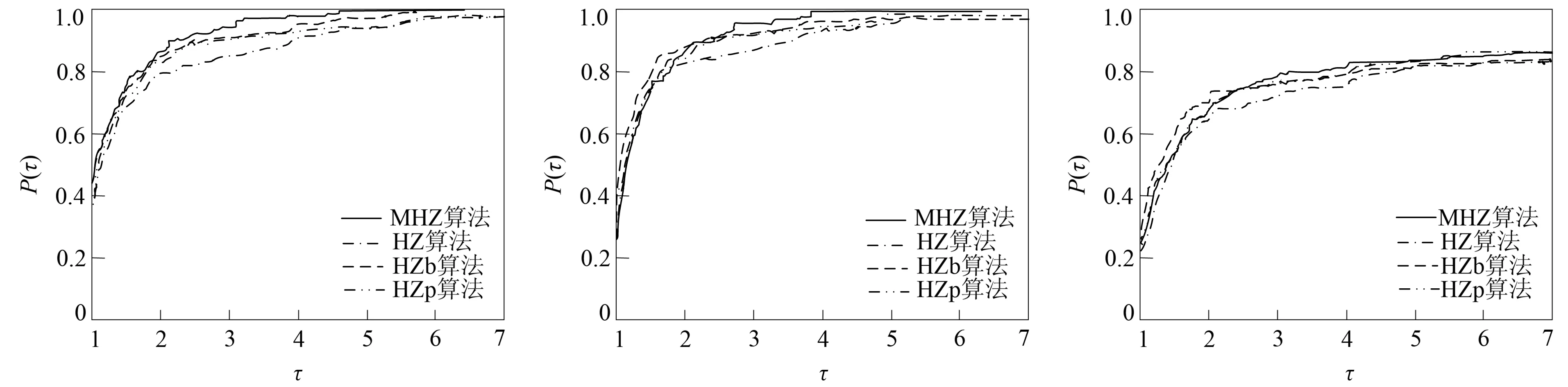
图1 4种算法的迭代次数(A)、 函数值计算次数(B)和CPU运行时间(C)性能评估Fig.1 Performance evaluation of iteration numbers (A), calculation numbers of function value (B) and CPU runtime (C) for four algorithms

综上所述, 本文基于文献[16]的搜索方向, 利用弱Wolfe-Powell线搜索构建了MHZ算法, 该算法具有如下优点： 1) 搜索方向具有充分下降性和信赖域性质； 2) 在常规假设条件下, 算法不仅对一般函数全局收敛, 在所给的条件下对一致凸函数具有R-线性收敛速度； 3) 数值实验结果表明, 在求解无约束优化问题上, MHZ算法比MZ算法、 HZb算法和HZp算法更有效.