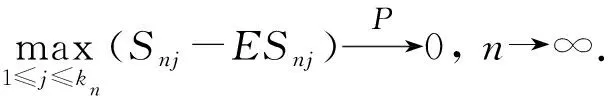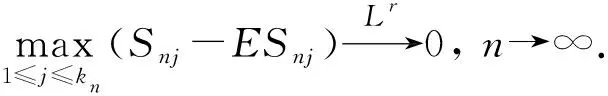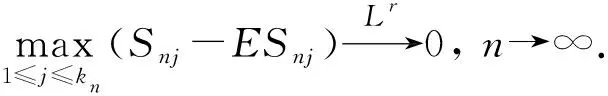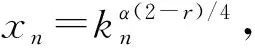NSD随机阵列加权和最大值的收敛性
2021-09-22胡学平王柳柳
胡学平, 王柳柳, 杨 瑞
(安庆师范大学 数理学院, 安徽 安庆 246133)
1 引言与预备知识
随机序列在金融风险和可靠性系统等领域应用广泛, 目前已取得了许多研究成果. 文献[1]在超可加函数的基础上, 引入了负超可加相依(negatively superadditive dependent, NSD)随机序列, 并通过一个例子表明NSD序列不蕴含NA(negatively associated)序列. 文献[2]研究表明, NA序列是NSD的. 因此, NSD序列是一类更广泛的相依序列. 文献[1]还举例说明了排列分布、 椭球等高分布、 多项分布、 Dirichlet分布、 多元超几何分布等在一定条件下均具有NSD序列的性质. 故研究NSD序列的极限性质有一定的理论意义. 文献[3]研究了NSD序列加权和的强收敛性质; 文献[4-8]分别研究了NSD变量的完全收敛性、 加权和的完全收敛性及其移动平滑过程的完全收敛性; 文献[9]和文献[10]分别给出了NSD序列的Rosenthal型矩不等式及其在NSD误差下EV(errors-in-variables)回归模型中估计量的相合性等结果; 文献[11]给出了NSD误差下线性模型最小绝对偏差(LAD)估计的线性表示.
如果对任意的x,y∈n, 有
φ(x∨y)+φ(x∧y)≥φ(x)+φ(y),
则称函数φ:n→是超可加的.其中x∨y表示各分量中取最大值者,x∧y表示各分量中取最小值者.
定义1[1]对于随机向量X=(X1,X2,…,Xn), 如果其满足
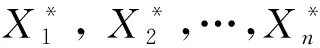
定义2[12]设{Xnk, 1≤k≤kn↑∞,n≥1}为一个随机变量阵列, {ank, 1≤k≤kn,n≥1}为一个实数阵列, 且对任意n∈, 存在常数C>0, 使得若满足

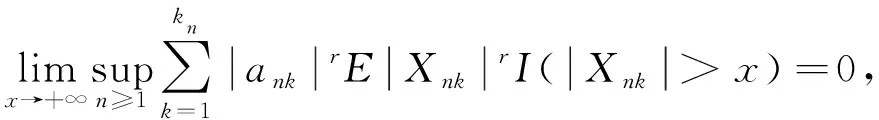
(1)

易证式(1)等价于下列两式成立:
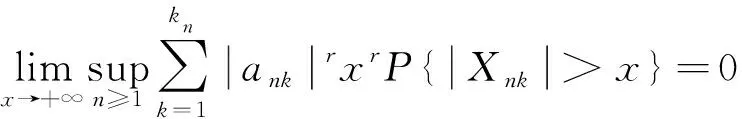
(2)

(3)
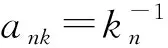
引理1[1]如果随机向量(X1,X2,…,Xn)是NSD的, 且f1,f2,…,fn均为非降函数, 则(f1(X1),f2(X2),…,fn(Xn))也是NSD的.
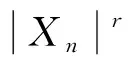
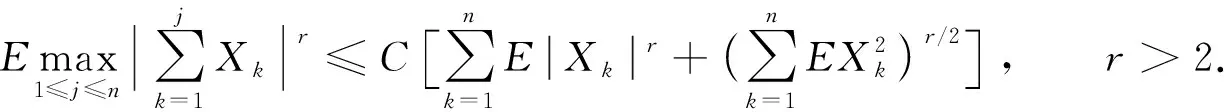

证明: 令
则对0 根据式(2), ∀ε>0, ∃M>0, 使得当t>M时, 有 由ε的任意性及0 定理1设{Xnk, 1≤k≤kn,n≥1}是一个行NSD随机阵列, {ank, 1≤k≤kn,n≥1}为一个实数阵列, 若对1≤r<2, 满足下列条件: 则 因为 故只需证明I1→0,I2→0. 根据Markov不等式及引理2, 有 根据引理3, 取p=2, 可得I11→0,n→∞.对于I12, 由条件(ii)和条件(i)可得 证明: 沿用定理1的记号, 根据Cr-不等式、 Jensen不等式、 引理2及式(1), 有 下面证明I3→0,I4→0,n→∞.与定理1中I1→0的证明类似可得I3→0,n→∞; 由式(1)可得I4→0,n→∞. 定理3设{Xnk, 1≤k≤kn,n≥1}是一个行NSD随机阵列, {ank, 1≤k≤kn,n≥1}为一个实数阵列,kn=O(n),n→∞.若对0 则 由Markov不等式及引理2, 有 由条件(ii)可知, 存在M>0, 使得当x>M时, 有 因为xn→∞, 从而∃n0, 使得当n≥n0时, 有xn>M, 再注意到δ>2,αr≥1, 于是有 条件(ii)等价于 因此对上述的n0和M, 当xn>M时, 结合kn=O(n), 有 类似定理3的证明可得: 推论3设{Xnk, 1≤k≤kn,n≥1}是一个行NA随机阵列, {ank, 1≤k≤kn,n≥1}为一个实数阵列,kn=O(n),n→∞.若对0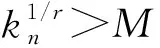
2 主要结果