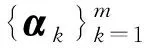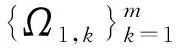非线性含参系统无穷多正周期解的存在性
2021-09-22杨伟
杨 伟
(西北师范大学 数学与统计学院, 兰州 730070)
0 引 言
一阶微分方程周期边值问题在生物医学、 经济学、 工程和物理学等领域应用广泛. 例如, 超音速流中飞行器壁板的气动弹性稳定性问题, 常微分方程组下的中等收入陷阱问题, 医学中处理心脏舒张问题常用的Carathéodory方程模型[1]
y′(t)=ay(t)+f(t),
(1)
以及生物学中研究种群捕食关系的Lotka-Volterra模型[2]

(2)
等. 其中关于单个方程周期边值问题正解的存在性研究目前已有许多成果[3-7]. 例如, Chen等[3]研究了一阶周期边值问题
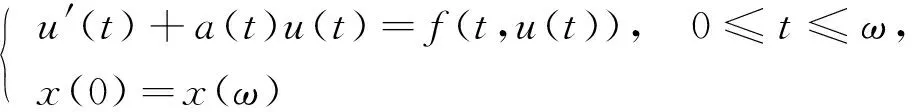
(3)

定理1[3]假设下列条件成立:

2) 存在χ≫0, 使得p∶=a+χ≻0;
3)f∈C([0,T]×[0,∞),[0,∞)),f(t,u)≥-χ(t)u.
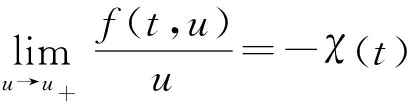
但关于系统周期边值问题正解的存在性研究目前文献报道较少[8-9]: Precup[8]研究了一阶非线性微分方程系统

(4)

定理2[8]假设存在αi,βi>0且αi≠βi(i=1,2), 使得
B1ωΓ1≤α1,A1ωγ1≥β1,
B2ωΓ2≤α2,A2ωγ2≥β2,
则问题(4)至少存在一个正周期解, 其中Ai,Bi,Γi(i=1,2)的表达式参见文献[4].

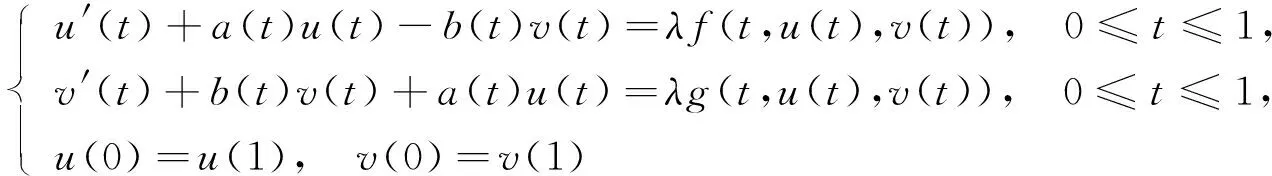
(5)
无穷多正周期解的存在性.本文总假设:
(H1)a,b: [0,1]→[0,∞)是连续函数且在[0,1]的任意子区间上不恒为零;
(H2)f,g: [0,1]×[0,∞)×[0,∞)→[0,∞)是连续函数.
为方便, 定义
z∶=(u,v)T, ‖z‖=‖u‖∞+‖v‖∞,
w∶=(f,g)T, ‖w‖1=‖f‖1+‖g‖1,
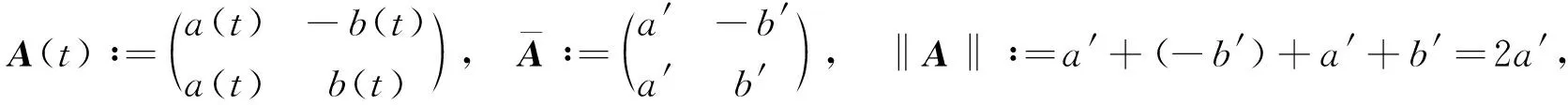
其中

设G(t,s)为非线性含参系统(5)对应的Green函数, 定义


1 预备知识
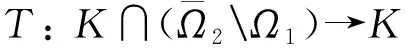
1) ‖Tu‖≥‖u‖,u∈K∩∂Ω1, ‖Tu‖≤‖u‖,u∈K∩∂Ω2;
2) ‖Tu‖≤‖u‖,u∈K∩∂Ω1, ‖Tu‖≥‖u‖,u∈K∩∂Ω2.
定义1[11]假设B是一个n×n常数矩阵, 定义矩阵指数eB为下列矩阵级数之和:

(6)
其中E为n阶单位矩阵,Bm是矩阵B的m次幂, 这里规定B0=E, 0!=1.
注1定义1的级数对所有的B都是收敛的.
注2对定义1中任意矩阵B, eB存在, 且
(eB)-1=e-B.
(7)
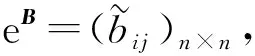
引理2[11]假设x=(x1,x2,…,xn),B是n阶常数矩阵, 则齐次线性微分方程组x′=Bx的基解矩阵为Φ(t)=eBt且Φ(0)=E.
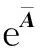
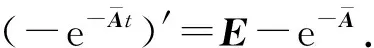

引理4假设条件(H1),(H2)成立, 则非线性含参系统(5)等价于积分方程

(8)
其中

(9)
证明: 系统(5)可表示为
z′(t)+A(t)z(t)=λw(t,z(t)),
(10)
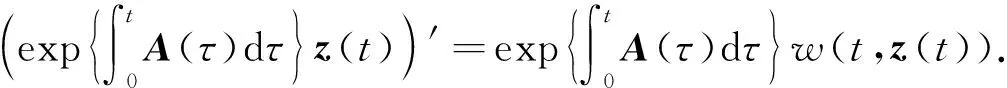
(11)
对式(11)关于0到t积分, 可得
对式(11)关于t到1积分, 可得
由u(0)=u(1)可得
从而
证毕.
定义Banach空间X如下: 设X={z(·)∈C([0,1],[0,∞)×[0,∞)):z(0)=z(1)}, 并设

是X中的锥.定义算子Tλ:K→X, 则

(12)
引理5假设条件(H1),(H2)成立, 则Tλ(K)⊂K.
证明: 假设z=(u,v)T∈K, 则

引理6假设条件(H1),(H2)成立, 则算子Tλ:K→K是一个紧算子.
证明: 考虑式(12).设S⊂C[0,1]是一个有界集, 则存在常数D>0, 使得对任意的z∈S, ‖z‖≤D.再结合w的连续性, 可得w在[0,1]×[0,D]中是一致连续的.从而可设存在常数F>0, 使得|w(t,z(t))|≤F,z∈[0,D], 于是
因此算子Tλ:K→K是一致有界的.
对任意的t1,t2∈[0,1](t1 记L∶=2λFM′, 则有 |Tλz(t1)-Tλz(t2)| |Tλz(t1)-Tλz(t2)|<ε. 因此, 算子Tλ:K→K是等度连续的.根据Arzela-Ascoli定理[11], 算子Tλ:K→K是紧的.证毕. 定理3假设m∈∪{+∞}, 且存在点列使得 rk+1 对于A∈(0,Λ2),B∈(Λ1,+∞)及每个自然数k, 假设w满足如下条件: (i) 当σrk<‖z‖ (ii) 当0<‖z‖ {Ω1,k}={z∈K: ‖z‖ {Ω2,k}={z∈K: ‖z‖ 对每个固定的常数k, 当z∈K∩∂Ω1,k时, 有 对任意的s∈[0,1], 结合条件(i), 有 即当条件(i)成立时, 有 ‖Tλz‖≥‖z‖. (13) 另一方面, 当z∈K∩∂Ω2,k时, 有 z(s)≤‖z‖, (14) 对任意的s∈[0,1], 结合条件(ii), 有 即当条件(ii)成立时, 有 ‖Tλz‖≤‖z‖. (15) 根据引理1中条件1), 可得算子Tλ有m个不动点.将这些不动点用αk表示, 则其满足 rk≤‖αk‖≤Rk,k=1,2,…,m. {Ω3,k}={z∈K: ‖z‖ 对每个固定的常数k, 当z∈K∩∂Ω3,k时, 式(14)成立.对任意的s∈[0,1], 结合条件(ii), 有 即当条件(ii)成立时, 式(15)成立.另一方面, 结合式(15)及引理1中条件2), 可得算子Tλ有(m-1)个不动点.将这些不动点用βk表示, 则其满足 Rk+1≤‖βk‖≤rk,k=1,2,…,m-1. 因此, 非线性含参系统(5)有(2m-1)个正周期解.证毕. 注3当m=+∞时, 非线性含参系统(5)有无穷多个正周期解.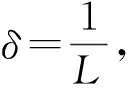
2 主要结果