唐 颖, 李永祥

(西北师范大学 数学与统计学院, 兰州 730070)

0 引 言

非线性项中含梯度项的一般椭圆边值问题描述了等离子体物理学、 气体动力学及固体物理学中的许多现象， 研究其解的存在性与唯一性有一定的理论意义. 本文讨论单位球上含梯度项的椭圆边值问题(BVP)：

(1)

径向解的存在性与唯一性, 其中:Ω={x∈N: |x|<1},+=[0,+∞),N≥2;f:I××+→为非线性连续函数,I=[0,1].

对非线性项中不含梯度项的特殊情形, 即简单椭圆边值问题:

其径向解的存在性已有较深入的研究[1-4].对非线性项含梯度项的情形, 当Ω为环形区域或球外部区域时, 文献[5-7]讨论了其正径向解的存在性, 其中文献[5-6]在非线性函数f(r,ξ,η)非负, 且允许f关于ξ,η超线性或次线性增长的条件下, 利用不动点指数理论获得了BVP(1)正径向解的存在性结果.但对于球域该结果并不成立.事实上, 文献[5]给出了一个典型的例子:

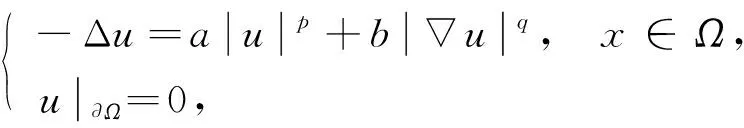
(2)

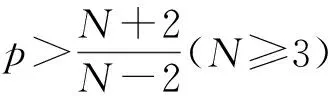
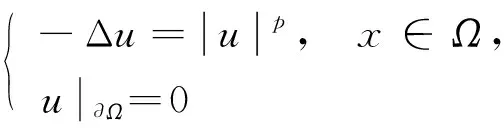
(3)

没有正径向解.此时, BVP(3)为BVP(2)中a=1,b=0的特例.因此, BVP(2)在球域上无正径向解.研究球域上椭圆边值问题径向解的存在性比环域及球外部区域上的椭圆边值问题径向解的存在性更复杂.目前， 关于球域上BVP(1)径向解的存在性结果研究报道较少.文献[8]用上下解方法研究了单位球上BVP(1)正径向解的存在性, 在非线性项f满足适当的不等式条件下, 获得了BVP(1)正径向解的存在性结果, 该不等式条件允许f(r,ξ,η)关于ξ和η负向超线性增长.本文研究单位球上椭圆BVP(1)径向解的存在性与唯一性, 在允许f(r,ξ,η)关于ξ和η超线性增长的条件下, 用Schauder不动点定理给出BVP(1)径向解及正径向解的存在性结果, 并通过进一步加强条件讨论该问题径向解的唯一性.

1 预备知识

对椭圆边值问题(1)的径向对称解u=u(|x|), 令r=|x|, 则其可转化为区间I上的常微分边值问题(BVP)：

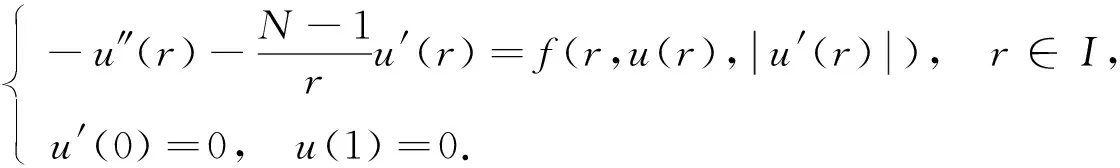
(4)

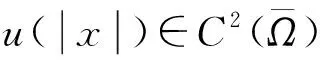
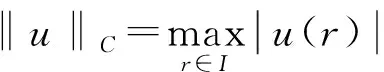
构成的Banach空间.

为讨论BVP(4), 先考虑相应的二阶线性边值问题(LBVP)：

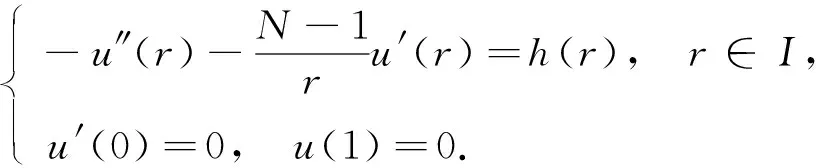
(5)

引理1[8]对∀h∈C(I), LBVP(5)有唯一解u∶=Sh∈C2(I), 解算子S:C(I)→C1(I)为线性全连续算子, 且

(6)

由式(6), 易得

(7)

引理2对∀h∈C+(I), 线性边值问题(5)的解u=Sh满足u≥0,u′≤0.

证明: 将方程(5)两边同乘rN-1, 得

-(rN-1u′(r))′=rN-1h(r),r∈I.

(8)

对方程(8)两边积分, 再应用方程(5)的边界条件, 得

因此u(r)≥0,u′(r)≤0,r∈I.证毕.

记

其中R1,R2为正常数, 则ΩR1,ΩR2为C1(I)中的凸闭集.

2 主要结果

假设条件:

|f(r,ξ,η)|≤R1, (r,ξ,η)∈I××+.

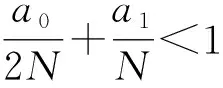
|f(r,ξ2,η2)-f(r,ξ1,η1)|≤a0|ξ2-ξ1|+a1|η2-η1|.

定理1设f:I××+→连续.若f满足条件(H1), 则BVP(1)至少有一个径向解.

证明: 对∀u∈ΩR1, 令

F(u)(r)∶=f(r,u(r),|u′(r)|),r∈I,

则F:ΩR1→C(I)连续, 且将有界集映为有界集.定义映射A=S∘F, 由引理1知,S:C(I)→ΩR1为线性全连续算子.因此, 算子A:ΩR1→ΩR1为线性全连续算子.由S的定义, BVP(4)的解等价于算子A的不动点.

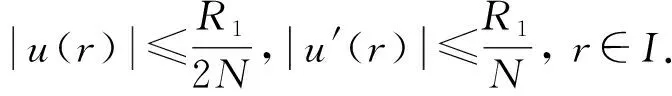
即A(ΩR1)⊂ΩR1.由Schauder不动点定理知,A在ΩR1中有不动点.该不动点为BVP(4)的解, 因此, BVP(1)有径向解.证毕.

定理2设f:I××+→连续.若f满足条件(H2), 则BVP(1)有唯一径向解.

证明: 先证存在性, (H2)⟹(H1).

令

(r,ξ2,η2)=(r,ξ,η), (r,ξ1,η1)=(r,0,0),

由条件(H2), 有

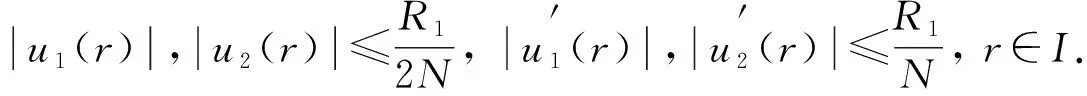
对式(9)两端取‖·‖C, 得

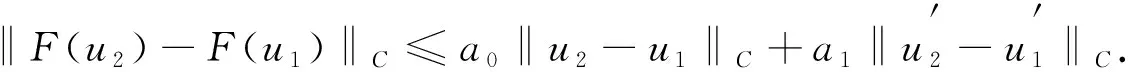
(10)

令u=u2-u1, 故

u=u2-u1=A(u2)-A(u1)=S(F(u2)-F(u1))=Sh.

由S的定义,u为h=F(u2)-F(u1)∈C(I)相应LBVP(5)的解.因此, 由式(6)及式(10), 得

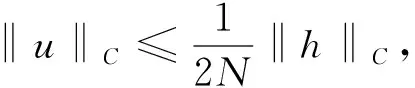
(11)

(12)

(13)

将式(11)乘a0, 由式(13), 得

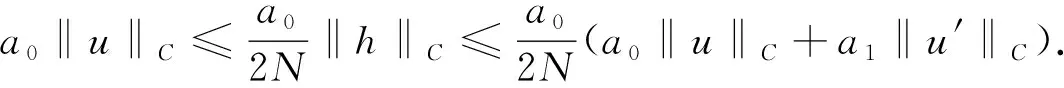
(14)

将式(12)乘a1, 由式(13), 得

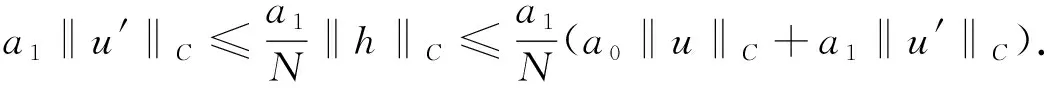
(15)

由式(13)～(15), 有

所以

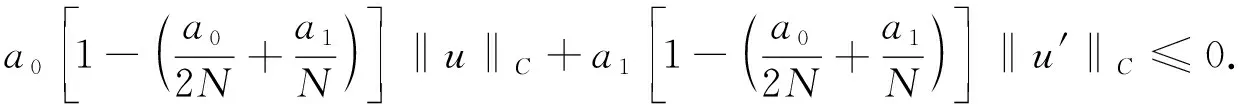
(16)

在定理1和定理2中, 非线性项f(r,ξ,η)关于ξ,η可超线性增长.当f(r,ξ,η)关于ξ,η均一次增长时, 有:

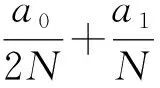
|f(r,ξ,η)|≤a0|ξ|+a1η+C, ∀(r,ξ,η)∈I××+.

定理3设f:I××+→连续.若f满足条件(H3), 则BVP(1)至少有一个径向解.

由引理2, LBVP(5)的解算子S为正算子.假设非线性项f非负, 下面给出BVP(1)正径向解的相关结果.

定理4设f:I×+×+→+连续.若f满足条件(H4), 则BVP(1)至少有一个正径向解.

证明: 对∀u∈ΩR2, 令

F(u)(r)∶=f(r,u(r),|u′(r)|),r∈I,

则F:ΩR2→C+(I)连续, 且将有界集映为有界集.定义映射A=S∘F, 由引理1知,S:C+(I)→ΩR2为线性全连续算子, 因此, 算子A:ΩR2→ΩR2为线性全连续算子.再由S的定义知, BVP(4)的解等价于算子A的不动点.

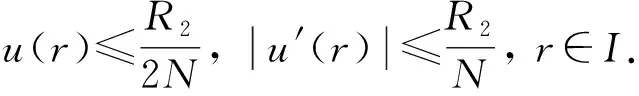
即A(ΩR2)⊂ΩR2.由Schauder不动点定理知,A在ΩR2中有不动点.该不动点为BVP(4)的正解, 因此, BVP(1)有正径向解.证毕.

在定理4中, 非线性项f(r,ξ,η)关于ξ,η也可超线性增长.当f(r,ξ,η)关于ξ,η均一次增长时, 有:

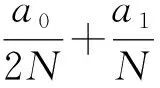
f(r,ξ,η)≤a0ξ+a1η+C, ∀(r,ξ,η)∈I×+×+.

定理5设f:I×+×+→+连续.若f满足条件(H5), 则BVP(1)至少有一个正径向解.

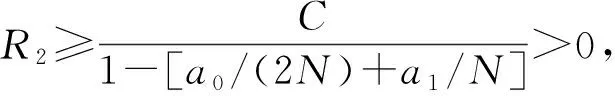
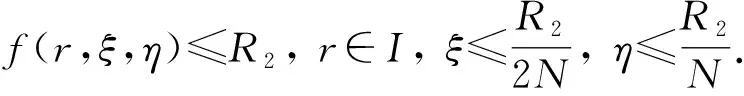
例1设N≥2, 考虑单位球Ω={x∈N: |x|<1}上含梯度项的椭圆边值问题：

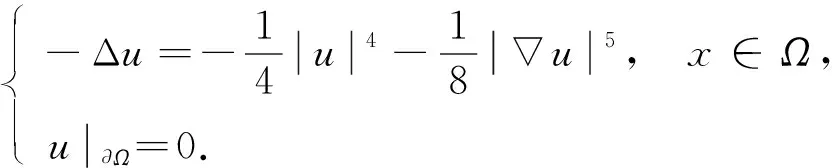
(17)

对应于BVP(1), 相应的非线性项为

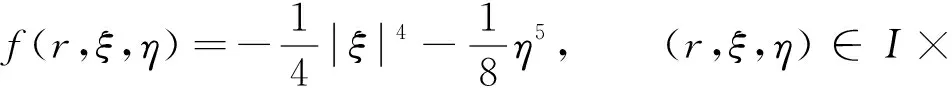
(18)

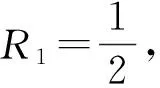
即∃R1>0, 使得f(r,ξ,η)满足条件(H1).因此由定理1知, BVP(17)有径向解.

例2设N≥2, 考虑单位球Ω={x∈N: |x|<1}上含梯度项的椭圆边值问题：

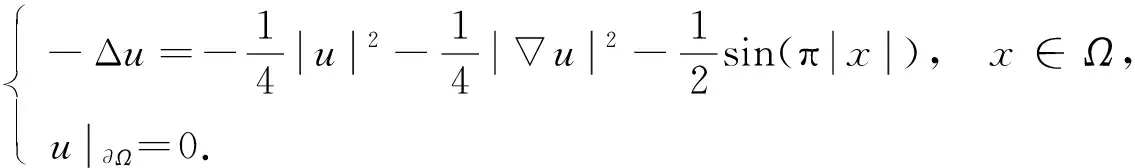
(19)

对应于BVP(1), 相应的非线性项为

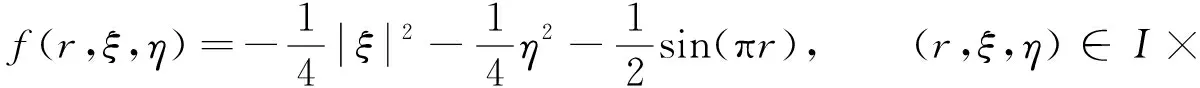
(20)

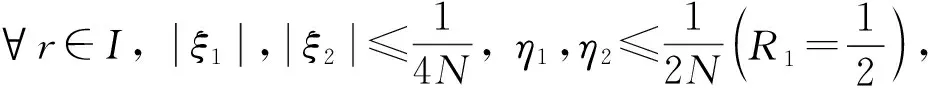
由式(20), 有

因此由式(21), 有