泊松过程和卡方拟合检验在地震间隔时间中的应用
2021-09-17刘芝秀
熊 可,刘芝秀
(1.南昌工程学院 理学院,江西 南昌 330099;2.江西财经大学 统计学院,江西 南昌 330077)
世界上几乎每天都在发生地震,其中的强地震往往会给人类社会造成比较大的危害,因而人们很早就开始了对地震的研究。虽然研究人员已从各个方面对地震进行了详细深入的研究,但是就目前的技术手段来讲,地震何时何地发生仍然是难以预测的,至少难以提前足够多的时间对地震进行预测。地震的发生具有很强的随机性,所以地震发生的统计规律一直是地震研究方面的一个热点,近几年仅我国研究人员就基于地震数据进行了持续不断的研究,发表了上百篇的论文[1],由此可见地震数据的研究是一个持续更新的过程。
在对地震数据进行研究的过程中,了解地震发生的时间是重要的,本文着重分析了两次相邻地震发生的时间间隔,利用随机过程模型和假设检验的方法验证得到了本文所用数据记录的地震间隔时间的一个概率分布,需要强调的是地震间隔时间的概率密度函数与所研究的数据是密切相关的,它有多种不同的经验概率分布[2-4],事实上,我们目前并没有立足物理机理推导证明出地震间隔时间的精确分布,因而不同的数据和经验分布都有助于地震间隔时间精确分布的发现与证明。
本文所使用的数据来自中国地震台网http://www.ceic.ac.cn/speedsearch?time=10,采集了2020年3月25日至2021年3月20日之间发生的破坏力较强的6.0级以上的地震信息。
1 预备知识
为讨论强震间隔时间的分布,首先介绍下重要的指数分布。
定义1指数分布
若随机变量X的密度函数为[5]
(1)
则称X服从指数分布,记作X~Exp(θ),其中参数θ>0。
它的期望E(X)为θ,分布函数为
(2)
检验一个总体的分布有如下卡方拟合检验方法
定义2分布拟合检验
检验的原假设为[5]
H0:总体X的分布函数是F(x;θ1,…,θr)
其中F形式已知,θ=(θ1,θ2,…θr)未知。在H0为真的情况下,将X的全部可能取值Ω分为子集A1,A2,…,Ak,满足∀AiAj=φ,i,j=1,2,…,k且k>r+1。
记fi(i=1,2,…,k)为x1,x2,…,xn落在Ai中的个数,即在n次相互独立的随机试验中,事件Ai={X的值落在子集Ai内}发生的次数为fi次,因此事件Ai发生的频率为fi/n。
另一方面,按照原假设中总体X的分布可计算事件Ai所发生的概率
P(Ai)=pi(θ1,θ2,…,θr)=pi(θ)=pi,
则得一个检验统计量如下
(3)
它近似地服从卡方分布,即
(4)
由此可知,在显著性水平α下,假设检验的拒绝域为
(5)
下文还需要与指数分布密切相关的泊松过程。
定义3泊松过程
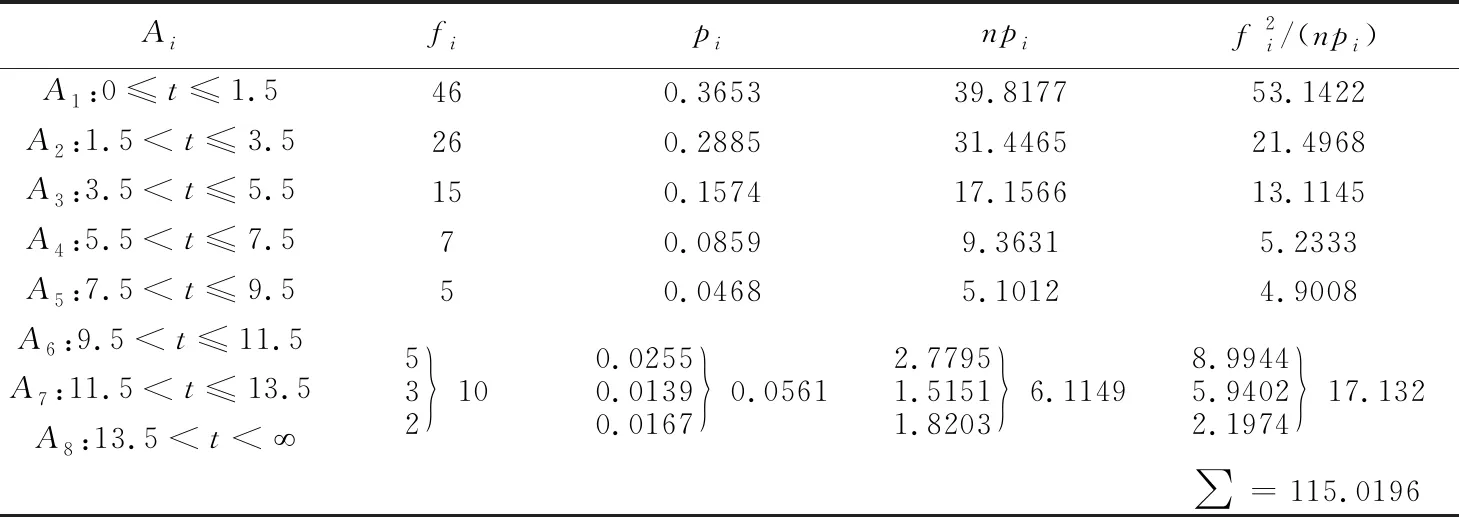
以N(t),t≥0表示在时间间隔(0,t]内出现的质点数,将增量N(t)-N(t0)记成N(t0,t),0≤t0 Pk(t0,t)=P{N(t0,t)=k},k=0,1,2,…. 如果N(t)满足如下条件 (1)对应任意选定的正整数n和任意选定的n个时刻0≤t0 N(t0,t1),N(t1,t2),…,N(tn-1,tn) 相互独立; (2)对于充分小的Δt P1{t,t+Δt}=P{N(t,t+Δt)=1}=λΔt+ο(Δt), 其中常数λ>0称为过程N(t)的强度,ο(Δt)是当Δt→0时关于Δt的高阶无穷小; (3)对于充分小的Δt 亦即对于充分小的Δt,在(t,t+Δt]内出现2个或2个以上质点的概率与出现一个质点的概率相比可以忽略不计; (4)N(0)=0.则称N(t)为强度为λ的泊松过程。 之所以说泊松过程与指数分布密切相关是因为强度为λ的泊松过程的相邻质点间间隔时间是相互独立的随机变量,且服从参数为1/λ的同一个指数分布。 从数据中可以得到全世界2020年3月25日至2021年3月20日一年间共发生6.0级以上强地震109次,平均每隔3.3天发生一次6.0级以上强地震,按间隔时间统计6.0级以上强地震次数如表1所示。 根据实际经验不难知道,6.0级以上强地震并不是每时每刻都在发生,存在一个时刻是没有发生6.0级以上强地震的,记此时刻为0,用N(t)表示在间隔时间(0,t]内发生的6.0级以上地震的次数,再类似定义3中定义记号N(t0,t)和Pk(t0,t)。显然,N(0)=0;而且,在很小的时间间隔内同时发生2次和2次以上的6.0级以上强地震的概率是非常微小的,事实上6.0级以上强地震发生一次本身就有持续的时间,瞬间间隔发生2次以上的6.0级以上强地震概率为0,即有 那么在不相重叠的时间区间上发生6.0级以上强地震关系是否明显呢?即 0≤t0 是否相互独立,一般情况下,它们明显不是独立的。因为发生大地震的地方接着会有余震,毗邻间隔时间发生的地震次数有很强的相关性,但此处考虑的是6.0级以上强地震,其余震很难维持在6.0级以上,所以可以近似的认为在不相重叠的时间区间上发生6.0级以上强地震次数是不相关的;另一方面,在一定的时间间隔内发生1次6.0级以上强地震的概率是可能的,而且时间间隔越大发生的概率就越大,概率大小与时间长短具有一定的正向关系。又由前述分析可知,在不相重叠的时间区间上发生6.0级以上强地震次数是独立的,又由于N(tn-1,tn)都是描述发生6.0级以上强地震次数这同一个现象,仅仅只是时间起点不一样,可以推知在等时间间隔上是否发生6.0级以上强地震这一随机现象是同分布的,所以对应给定的时间间隔发生6.0级以上强地震的概率应该与时间间隔有一个固定的比率,即 P{N(t,t+Δt)=1}=λΔt+ο(Δt) 其中λ为一个比率参数,即强度。 从以上经验可以推断,发生6.0级以上强地震的过程正是一个泊松过程,由此可知两次相邻的6.0级以上强地震的间隔时间,记其为T,服从指数分布,设其密度函数为 其中λ=1/θ。 下面进一步对此做假设检验,假设T服从指数分布,即原假设为 在假设情况下,T的全部可能取值Ω为[0,+∞)。将[0,+∞)分为如下不相交的小区间: A1=[0,1.5],A2=(1.5,3.5],A3=(3.5,5.5],A4=(5.5,7.5], pi=P(Ai)=P{ai 得 表2 χ2统计量计算表 上面在显著性水平α=0.05下验证了相邻两次6.0级以上强地震发生的间隔时间T是服从指数分布的,其实用指数分布拟合间隔时间分布的具体偏差是多大还可以换一个更直观的角度进行观察,可用给定间隔时间的理论与实际偏差次数和实际次数的比值来评估指数分布拟合间隔时间分布的效果。由表2第2列和第4列数据四舍五入得间隔时间给定的理论次数和实际次数如表3。 由表3可以看到,给定间隔时间的理论与实际次数的差额为表3第4行差额的和,即18次,而实际次数为第2行实际频数的和109次,其偏差比率为 表3 间隔时间给定的理论与实际次数对比 上述偏差率小再次说明了用指数分布拟合6.0级以上强地震间隔时间分布的效果是良好的。2 理论分析结果与数据验证


A5=(7.5,9.5],A6=(9.5,11.5],A7=(11.5,13.5],A8=(13.5,∞).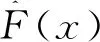

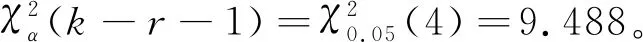
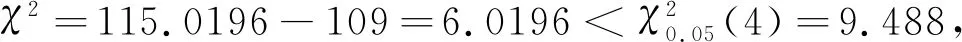
3 拟合评价