(刘永建)

Guangxi Colleges and Universities Key Laboratory of Complex System Optimization and Big Data Processing,Yulin Normal University,Yulin 537000,China E-mail:liuyongjianmaths@126.com

Stanislaw MIóRSKI

College of Applied Mathematics,Chengdu University of Information Technology,Chengdu 610225,China Jagiellonian University in Krakow,Chair of Optimization and Control,ul.Lojasiewicza 6,30348 Krakow,Poland E-mail:stanislaw.migorski@uj.edu.pl

Van Thien NGUYEN

Departement of Mathematics,FPT University,Education Zone,Hoa Lac High Tech Park,Km29 Thang Long Highway,Thach That Ward,Hanoi,Vietnam.E-mail:Thiennv15@fe.edu.vn

Shengda ZENG (曾生达)†

Guangxi Colleges and Universities Key Laboratory of Complex System Optimization and Big Data Processing,Yulin Normal University,Yulin 537000,China Jagiellonian University in Krakow,Chair of Optimization and Control,ul.Lojasiewicza 6,30348 Krakow,Poland E-mail:zengshengda@163.com

Abstract The goal of this paper is to study a mathematical model of a nonlinear static frictional contact problem in elasticity with the mixed boundary conditions described by a combination of the Signorini unilateral frictionless contact condition,and nonmonotone multivalued contact,and friction laws of subdifferential form.First,under suitable assumptions,we deliver the weak formulation of the contact model,which is an elliptic system with Lagrange multipliers,and which consists of a hemivariational inequality and a variational inequality.Then,we prove the solvability of the contact problem.Finally,employing the notion of H-convergence of nonlinear elasticity tensors,we provide a result on the convergence of solutions under perturbations which appear in the elasticity operator,body forces,and surface tractions.

Key words Mixed variational-hemivariational inequality;H-convergence;homogenization;Clarke subgradient;Lagrange multiplier;elasticity operator

1 Introduction

The aim of this paper is to investigate a mathematical model described by a system consisting of a hemivariational inequality and a variational inequality in re flexive Banach spaces.Such systems appear as weak formulations of various static contact problems in the theory of elasticity and are motivated by a menagerie of friction and contact boundary conditions.We will analyze a new nonlinear frictional contact problem which is described by a nonlinear elastic constitutive law and mixed boundary conditions.The latter combine the Signorini unilateral frictionless contact condition,nonmonotone multivalued contact and friction laws with locally Lipschitz super potentials.

Note that the theory of hemivariational inequalities started in the 1980s with the contributions of P.D.Panagiotopoulos[32–34],and since then it has considerably enriched the development of variational inequalities in many directions.The main idea behind hemivariational inequalities was to remove the hypotheses on the differentiability and convexity of energy functionals and to derive the variational formulations of various mechanical problems with the help of the generalized subgradient of Clarke.Hemivariational inequalities cover boundary value problems for PDEs with nonconvex,nonmonotone and possibly multivalued laws,in particular,problems where the Clarke subgradient is a pseudomonotone operator;see[30].The literature on hemivariational inequalities has been signi ficantly enlarged in the last forty years,mainly because of their multiple applications to a wide fields;see monographs[26,27,30,36]for analysis of various classes of such inequalities,and,see,for example,[3–5,13–16,18–20,28,29,38–40].

The novelties of this paper are several.First,we formulate the frictional contact problem as a mixed variational-hemivariational inequality.This formulation of the contact model under consideration is new and is studied here for the first time.Another formulation,in the form of a single variational-hemivariational inequality,can be found in[7,21–24,27,30,36].Second,we apply a recent abstract result from[2]and prove the existence of solutions to a mixed variational-hemivariational inequality.Third,we demonstrate a result on the convergence of solutions to the contact problem under perturbations which appear in the elasticity operator,body forces,and surface tractions.We will apply the notion of

H

-convergence of nonlinear elasticity tensors,as outline in,[1,6,8,11].Using this notion allows one to deal with the homogenization process modeling the periodic structures.The applications of

H

-convergence to mixed variational-hemivariational inequalities has not been studied.

Mixed variational-hemivariational inequalities have been considered very recently in[2,25].The application of homogenization to pure boundary hemivariational inequalities in linear elasticity can be found in[17].Finally,we note that the recent results on the mathematical theory of contact mechanics are available in recent monographs[12,27,35]and the references therein.

The structure of the paper is as follows:in Section 2,a complicated frictional elastic contact problem is introduced and studied for which we prove the theorem of the existence of solutions for the contact problem under consideration;Section 3 deals with the convergence of solutions to the model under the

H

-convergence of nonlinear elasticity tensors,perturbations in the body forces,and surface tractions.

2 A Nonlinear Frictional Elastic Contact Model

This section is devoted to studying a complicated static frictional contact problem in elasticity.We first recall a recent theoretical result concerning the existence and uniqueness of a mixed variational-hemivariational inequality.Then,we deliver the classical mathematical formulation for the elastic contact problem under consideration.In addition,under suitable assumptions,we obtain the weak formulation of the contact problem,which is formulated by a mixed variational-hemivariational inequality.Finally,an existence and uniqueness theorem for the contact problem is established.

Throughout this paper we use the notion of a generalized directional derivative and the Clarke generalized subgradient recalled below;see,for example,[10,27].Let

J

:

X

→R be a locally Lipschitz function on a Banach space

X

.The generalized directional derivative of

J

at

x

∈

X

in the direction

v

∈

X

is de fined by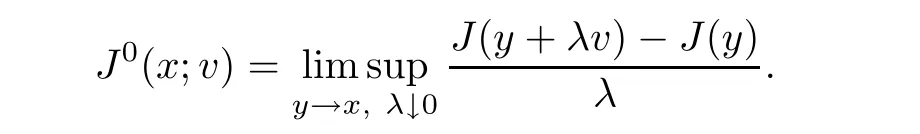

The generalized subgradient of

J

at

x

is a subset of the dual space

X

,given by

Let

V

,

E

and

X

be re flexive Banach spaces,and Λ be a nonempty subset of

E

.We denote by〈·

,

·〉the duality pairing between

V

and its dual

V

.Given an operator

A

:

V

→

V

,a function

J

:

X

→R,a bilinear function

b

:

V

×

E

→R,an operator

γ

:

V

→

X

and an element

f

∈

V

,we consider the following mixed variational-hemivariational inequality:

Problem 2.1

Find(

u,λ

)∈

V

×Λ such that the following two inequalities hold:

The following theorem is a direct consequence of[2,Theorem 15]:

Theorem 2.1

Let Λ be a nonempty,closed and convex subset of

E

with 0∈Λ.Assume that the following conditions are ful filled:

∂J

:

X

→2isbounded,that is,

∂J

maps the bounded subsets of

X

into bounded subsets of(i)

J

:

X

→R is a locally Lipschitz function such that its generalized subdifferential operator

X

∗;

(iv)

γ

:

V

→

X

is a linear and continuous operator.Then,for each

f

∈

V

,Problem 2.1 has at least one solution(

u,λ

)∈

V

×Λ,which is unique in its first component.Next,we move our attention to studying a static frictional elastic contact problem.We provide a description of this problem,give its weak formulation,and prove an existence result.We suppose that a nonlinear elastic body occupies,in the reference con figuration,a bounded domain Ω in R,

d

=2,3 with Lipschitz boundary Γ=

∂

Ω,which is considered to be partitioned into four mutually disjoint measurable parts Γ,Γ,Γand Γwith meas(Γ)

>

0.In this paper,the indices

i

,

j

,

k

,

l

run from 1 to

d

,unless stated otherwise,and the summation convention over repeated indices is used.In what follows,we shall adopt the standard notation:ν and Sdenote the unit outward normal on the boundary

∂

Ω,and the space of symmetric tensors of second order on R,respectively.The inner products and norms in Rand Sare given by

Throughout this paper,we denote by u=(

u

),σ=(

σ

),and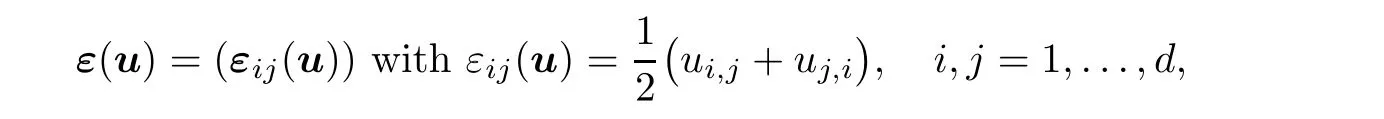

accordingly.Similarly,the normal and tangential components of stress field σ on the boundary are de fined by

respectively.

We now formulate the classical mathematical model of the static contact problem.

Problem 2.2

Find a displacement field u:Ω→Rand a stress field σ:Ω→Ssuch that

We describe shortly the physical meaning of the equations and conditions in Problem 2.2.Equation(2.4)represents a nonlinear elastic constitutive law in which A stands for a nonlinear elasticity operator.Moreover,equality(2.5)is the equation of equilibrium,where the symbol“Div”denotes the divergence operator,that is,

and frepresents the density of volume forces.The standard boundary conditions(2.6)and(2.7)reveal the physical phenomena that the elastic body is fixed on Γand that it is subjected to surface tractions of density fon Γ.The contact condition(2.8)is the so-called unilateral contact with frictionless effect;for more details concerning this contact boundary condition,we refer to[12,27,36].Condition(2.9)represents a multivalued subdifferential contact condition in the normal direction of Γ,where

j

is assumed to be locally Lipschitz with respect to its last variable,which is not convex in general.Furthermore,the condition in(2.10)is a friction law governed by the generalized gradient of a locally Lipschitz potential

j

.Such a frictional condition has been investigated many times,for instance,in[17,27,36]and the references therein.

To explore the unique solvability of Problem 2.2,we now impose the following assumptions:

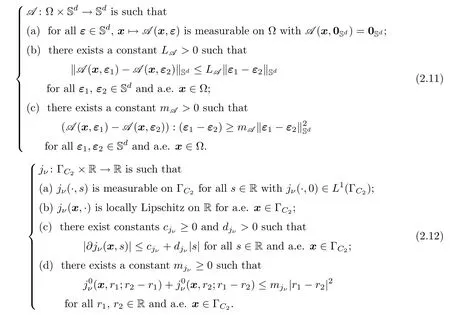
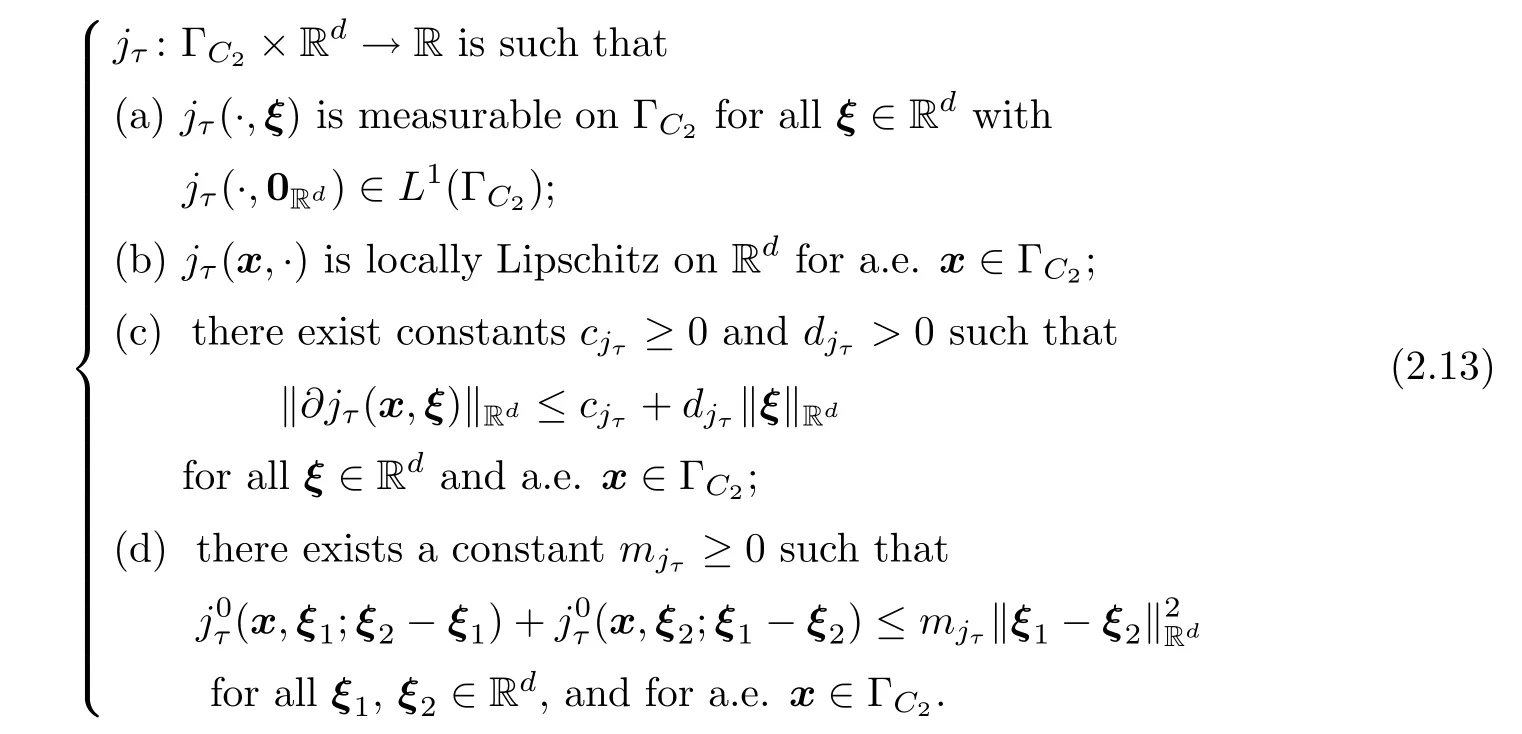
Finally,we suppose that the densities of volume forces and surface tractions have the following regularity:

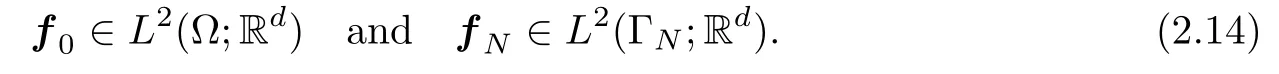
To establish the variational formulation of Problem 2.2,we consider the function spaces

Obviously,H is a Hilbert space with the inner product and corresponding norm given by

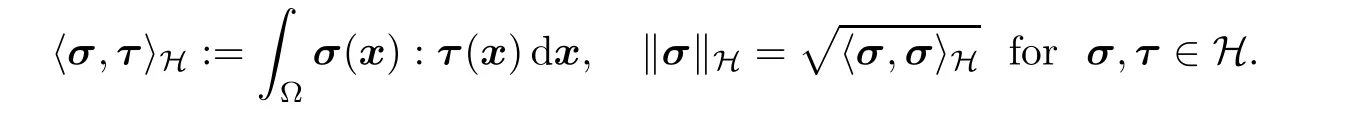
is a Hilbert space as well.

Throughout the paper,we denote by γ:

V

→

L

(Γ;R)the trace operator for vector-valued functions.Furthermore,we introduce a map

β

:

V

→

L

(Γ)de fined by

and we denote by

Y

=

H

2(Γ)⊂

L

(Γ)the image of

V

under the function

β

,that is,

By virtue of the trace theorem,it is not difficult to find that the space

Y

,endowed the norm

is a re flexive Banach space.Let

E

be the dual space of

Y

,and de fine a subset

S

of

V

by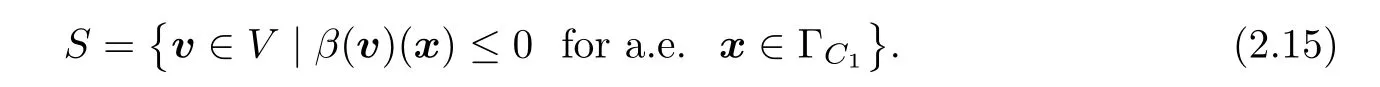

Moreover,we introduce a closed and convex subset Λ of

E

de fined as

where〈·

,

·〉represents the duality pairing between

E

and

Y

.Subsequently,we assume that(u

,

σ)are smooth enough on Ω such that(2.4)–(2.10)are satis fied.For any v∈

V

fixed,multiplying the equation of equilibrium(2.5)by v−u and applying the Green formula(see,for example,[27,Theorem 2.25]),it turns out that

The boundary conditions(2.6)and(2.7)imply

where f∈

V

is de fined by

which is obtained by applying the Riesz representation theorem.Next,taking into account(2.9),(2.10),the equality

and the de finition of the Clarke subgradient

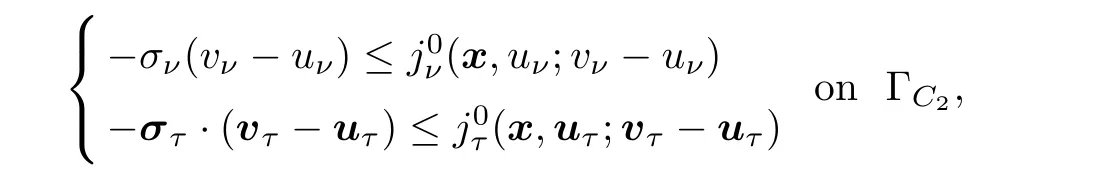
we obtain

Consider a multiplier

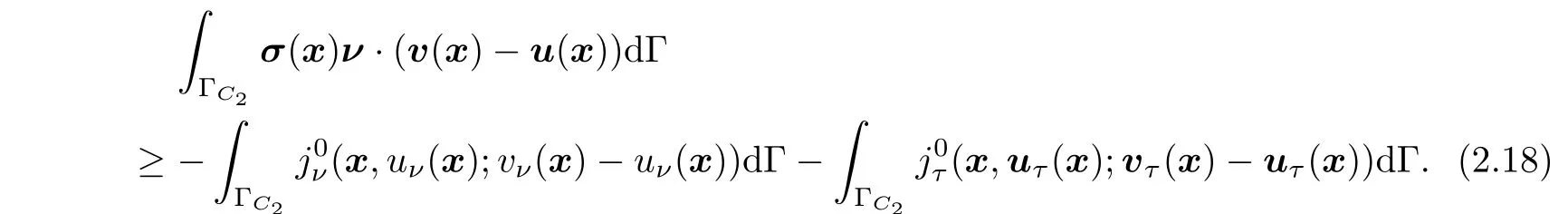
λ

∈

E

de fined by

and a bilinear function

b

:

V

×

E

→R given by

From the above equalities and the frictionless boundary condition(2.8),it follows that

Combining(2.8),(2.15),(2.16),(2.19)and(2.20),we deduce that

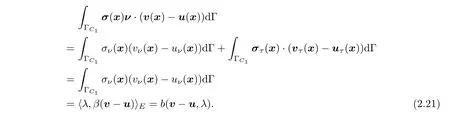
λ

∈Λ,u∈

S

,and

From(2.4),(2.17),(2.18),(2.21)and(2.22),we derive the following variational formulation of Problem 2.2:

Problem 2.3

Find a displacement field u∈

V

and a multiplier

λ

∈Λ such that

Using Theorem 2.1,we conclude the following existence result for Problem 2.3(let γbe the trace operator from

V

to

L

(Γ;R)):

Theorem 2.2

Assume that(2.11)–(2.14)hold.If,in addition,the smallness condition is satis fied,then Problem 2.3 has at least one solution(u

,λ

)∈

V

×Λ,which is unique in its first component.

Proof

We shall invoke Theorem 2.1 to conclude the desired assertion.To this end,we will verify that all conditions of Theorem 2.1 are valid.We now de fine an operator

A

:

V

→

V

and a function

J

:

X

→R by

where

X

=

L

(Γ;R).It follows from hypotheses(2.12),(2.13)and[27,Theorem 3.47]that

J

is a locally Lipschitz function such that

for all u,v∈

X

.Also,from hypotheses(2.12)(c),(2.13)(c)and[27,Theorem 3.47(vi)],we find constants

α

≥0 and

β

>

0 such that

which implies that the subdifferential operator

∂J

:

X

→2is bounded.Moreover,assumptions(2.12)(e)and(2.13)(e),and the inequality(2.28),reveal that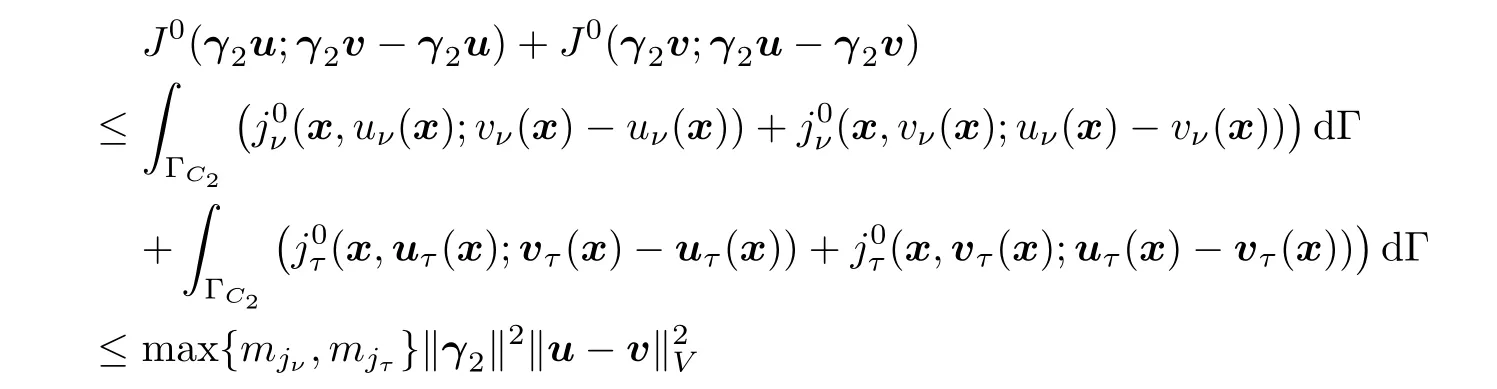

for all u,v∈

V

.This leads to the inequality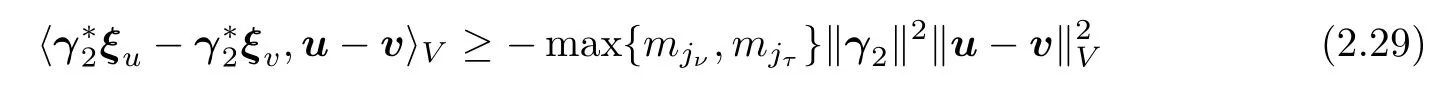

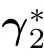
On the other hand,the hypothesis(2.11)(b)guarantees that

for all u,v∈

V

.This means that

A

is a Lipschitz continuous operator.Since A(x

,

0)=0for a.e.x∈Ω,this results in us getting that‖

A

u‖≤

L

‖u‖for all u∈

V

.Furthermore,hypothesis(2.11)(c)implies that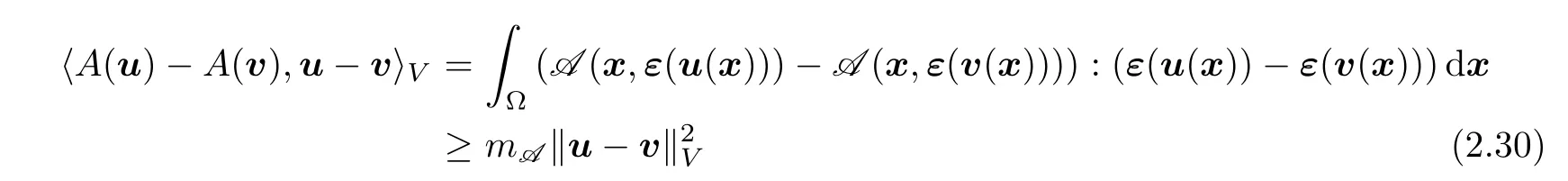

for all u,v∈

V

.Combining(2.29)and(2.30),one has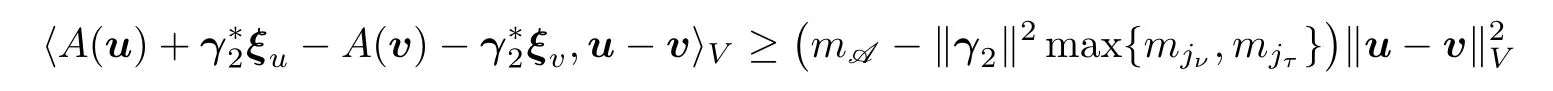

for all ξ∈

∂J

(γu),ξ∈

∂J

(γv),and u,v∈

V

.

This identity leads to

Letting

ρ

∈

E

be arbitrary,we have

Hence,all conditions of Theorem 2.1 have been veri fied.We are now in a position to apply Theorem 2.1 to conclude that the following problem has at least one solution(u

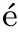
,λ

)∈

V

×Λ,which is unique in its first component:

It follows from(2.28)that(u

,λ

)∈

V

×Λ is also a solution to Problem 2.3.Finally,we will show that the first component u of the solution to Problem 2.3 is unique.Let(u

,λ

),(u

,λ

)∈

V

×Λ be two solutions to Problem 2.3.Then,we have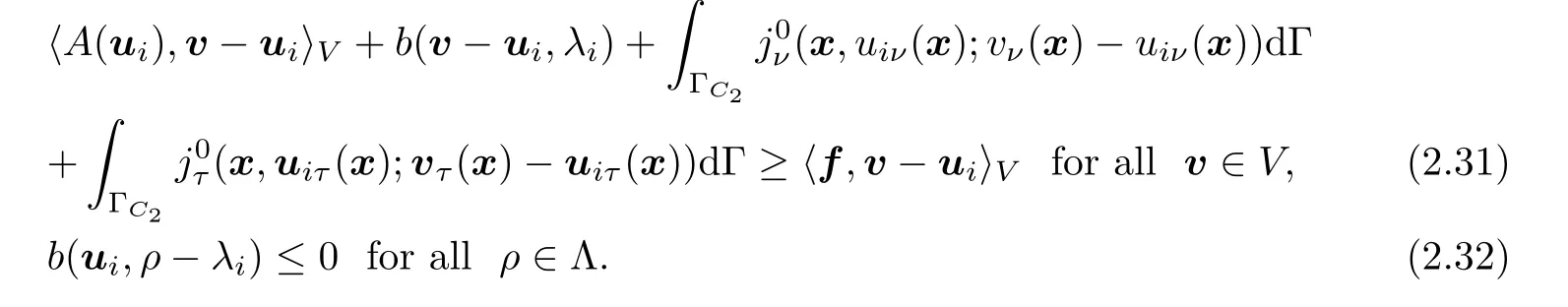

Inserting

ρ

=

λ

and

ρ

=

λ

into(2.32)for

i

=1 and 2,respectively,we add the resulting inequalities to obtain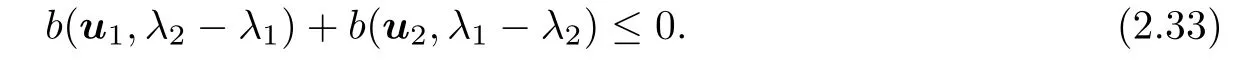

Finally,taking v=uand v=uin(2.31)for

i

=1 and 2,respectively,and combining the resulting inequalities with(2.33),we derive

hence u=u.This completes the proof.

3 Convergence Analysis

In this section,we are interested in the study of the behavior of a sequence of solutions to the nonlinear elastic contact problem,Problem 2.2,under the perturbations in the nonlinear elasticity operator A,volume forces f,and surface tractions f.

Given a sequence{A}⊂

S

,

k

∈N,and a function g∈

H

(Ω;R),consider the Dirichlet problem with homogeneous boundary condition

It is worth mentioning that the notion of the

H

-convergence of elasticity operators is a critical mathematical tool for studying the homogenization of periodic problems.For example,if A∈

S

is such that A(·

,

ε)is periodic and

ε>

0,then,putting

we have that A

H

-converges to Aas

ε

→0,where Ais independent of the spatial variable.The following theorem reveals that each sequence in

S

is relatively compact in the sense of

H

-convergence:

Furthermore,we recall a fundamental convergence result,which will play an important role in the main result of this section;its proof can be found in[1,Lemma 1.43]and[10,Lemma 11].

Lemma 3.4

(Compensated compactness)Let{z}be a sequence converging to zweakly in

H

(Ω;R),and let{h}be a sequence converging to hweakly in H such that

Then,the sequence{h:ε(z)}converges to h:ε(z)in the sense of distributions on Ω,namely,Z

For more details on

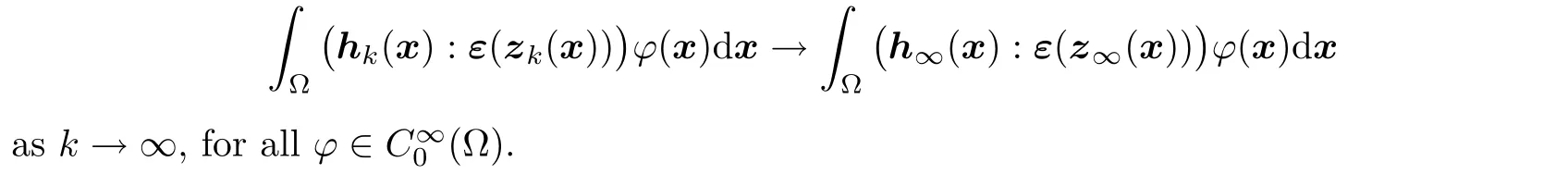
G

and

H

-convergences,we refer to[8,9,41].Let

k

∈N∪{∞}be a parameter and let{A}be a sequence in

S

.We consider the following perturbed problem:find a displacement field u∈

V

and a multiplier

λ

∈Λ such that

Since the constraint set in inequality(3.3)is the whole space

V

,problem(3.3),(3.4)can be equivalently formulated as

Theorem 3.5

Let{(f

,

f)}and{A}be two sequences in

H

×

L

(Γ;R)and

S

,respectively.Assume that hypotheses(2.11)-(2.14)and(2.25)are ful filled.If,in addition,the following convergences are satis fied:

then the sequence(u

,λ

)∈

V

×Λ of solutions to problem(3.5),(3.6)for

k

∈N,associated with(f

,

f),has a subsequence converging weakly in

V

×Λ as

k

→∞to the solution(u

,λ

)∈

V

×Λ to the following problem:

Proof

For each

k

∈N∪{∞},Theorems 2.1 and 2.2 show that problem(3.5)-(3.6)has at least one solution(u

,λ

)∈

V

×Λ for each

k

∈N,which is unique in its first component.Let f∈

V

be such that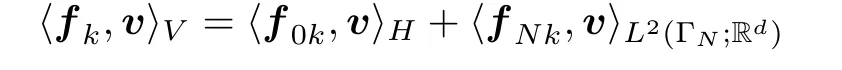

for all v∈

V

,for all

k

∈N.The proof will be carried out in three steps.

Step 1

The sequences{u}and{

λ

}are both uniformly bounded in

V

and Λ,respectively.Recall that 0∈Λ,so we take

ρ

=0in(3.6)to get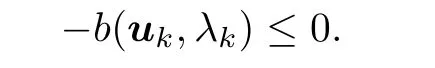

Inserting v=−uinto(3.5),this yields that

Taking into account the last two inequalities,one has

Moreover,inequalities(2.12)(d)and(2.13)(d)imply that

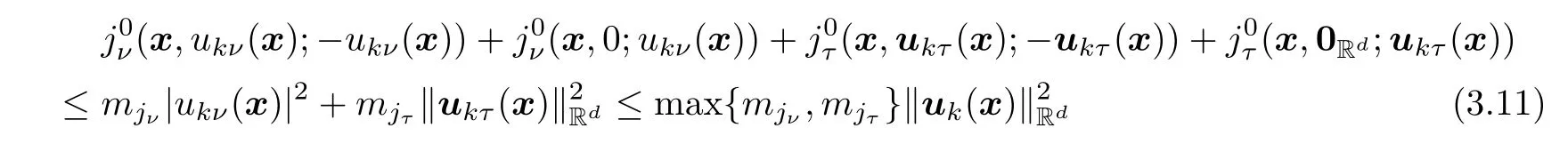
for a.e.x∈Γ.On the other hand,(2.12)(c)and(2.13)(c)entail that

for a.e.x∈Γ(C).Combining(3.11)and(3.12),we have

Next,we shall prove the uniform boundedness of{

λ

}in Λ.For any w∈

V

{0},taking v=−w in(3.5),one has

From the boundness of{u},we obtain

for all w∈

V

{0},where

M

>

0 is such that

for all

k

∈N.Passing to the supremum in(3.14)with w∈

V

{0},this yields that

which means that the sequence{

λ

}is uniformly bounded in Λ.The re flexivity of the spaces

V

,

E

and H implies that there exist subsequences,still denoted in the same way,and elements u∈

V

,

λ

∈Λ and η∈H such that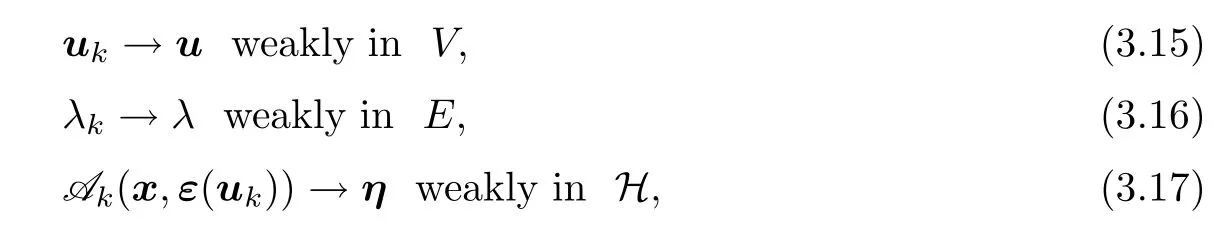

as

k

→∞.

Step 2

We will identify the limit η in(3.17)and show that η(x)=A(x

,

ε(u))for a.e.x∈Ω.

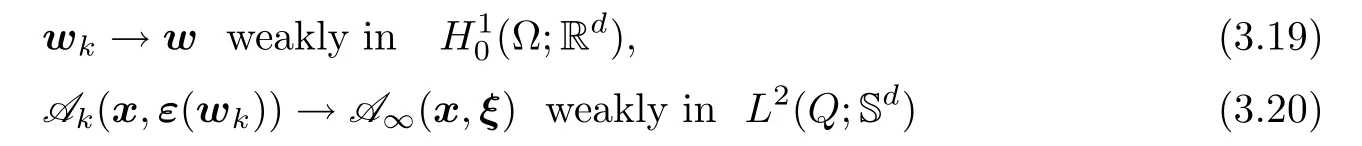
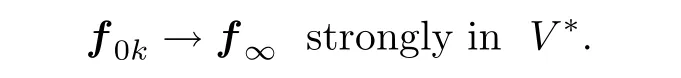
The latter,combined with the facts that,

as well as the compensated compactness result of Lemma 3.4,shows that

For any δ∈S,we insert ξ=ξ:=

t

δ+(1−

t

)ε(u)with

t>

0 into the above inequality to obtain

Passing to the limit as

t

→0,we obtain

This means that

Therefore,from(3.17),we verify the desired conclusion.

Step 3

We will prove that the pair(u

,λ

)is a solution to problem de fined in(3.8)and(3.9).Note that the operators γ:

V

→

L

(Γ;R)and

β

:

V

→

L

(Γ)are both compact,thus,by convergence(3.15),it follows that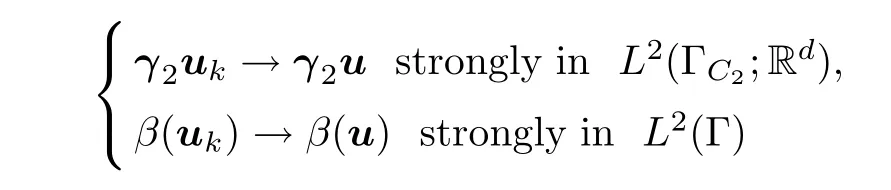

as

k

→∞.This implies that

On the other hand,it follows from the converse Lebesgue-dominated convergence theorem(see,for example,[27,Theorem 2.39])that by passing to a subsequence if necessary,we have

Since the sequence{u}is uniformly bounded in

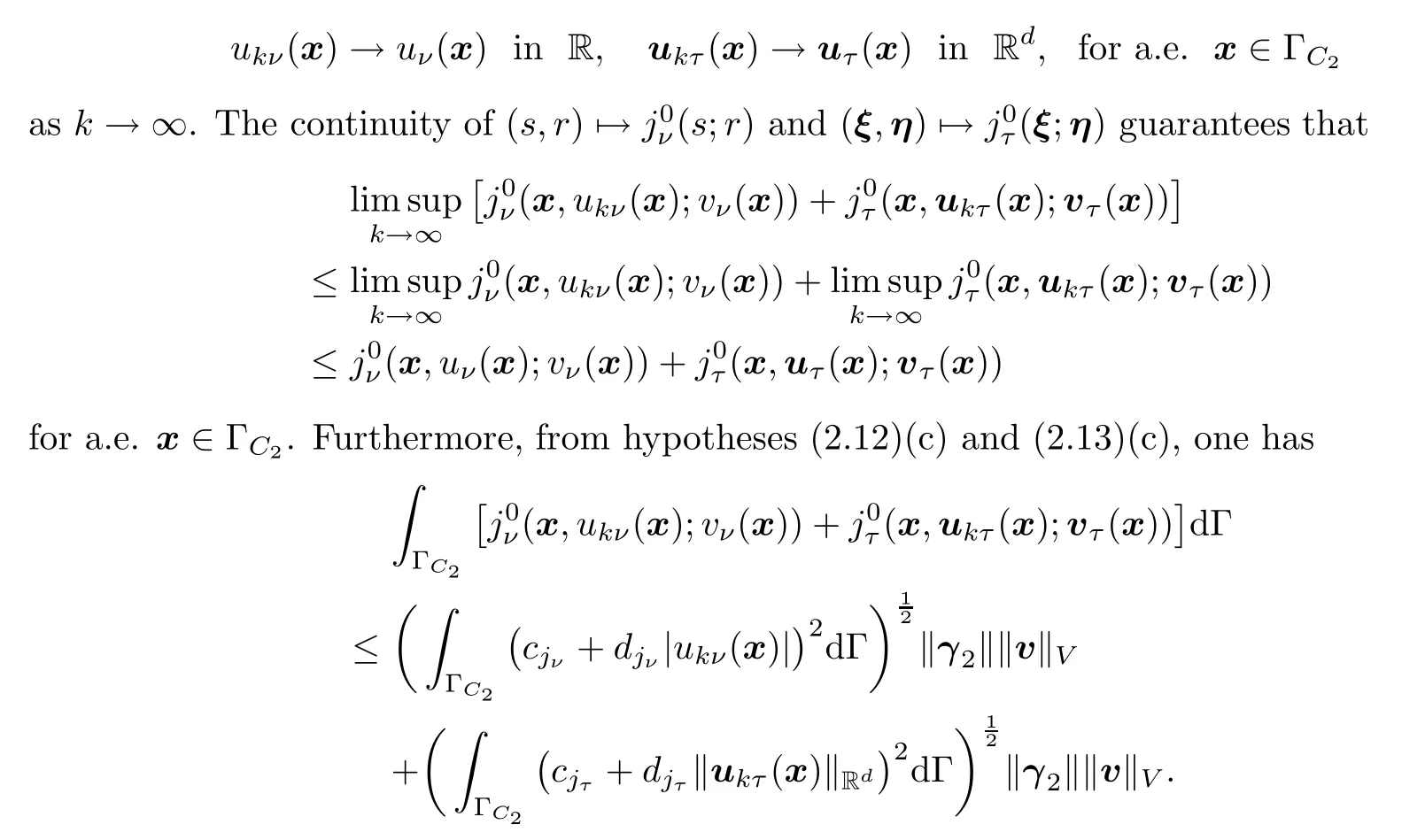
V

,by the Fatou lemma(see,for example,[27,Theorem 1.64])we get that

From(3.17),(3.22)and(3.23),it follows that

for all v∈

V

.Combining(3.21)and(3.24),we conclude that(u

,λ

)∈

V

×Λ is a solution to problem(3.8),(3.9).

Remark 3.6

From Theorem 2.2,we can see that the first component of a solution for(3.8)and(3.9)is unique.This implies that each subsequence of{u}converges weakly to the same limit u.Consequently,we conclude from[35,Theorem 1.20]that the whole sequence{u}converges weakly in

V

to u.

Acknowledgements

This article is honor of the 75th anniversary of Yulin Normal University.