胡珍妮，常在斌，崔娟

（西安交通工程学院，陕西 西安 710300）

自回归移动平均模型(Autoregressive Moving Average，ARMA)的频谱估计被认为是一些应用领域中值得关注的话题，如工程、计量经济学等。不同的方法已经被研究，包括两个方面：最优方法（如最大似然估计）、基于尤尔-沃克方程的次优方法（使用线性方程对参数进行估计）。

ARMA过程的估计方法被广泛研究，特别是参数的单独估计[1-2]，其中文献[3-4]使用尤尔-沃克方程估计AR的过程参数，然后通过Durbin方法估计MA过程参数。在这些方法中，应用最广泛的是改进的尤尔-沃克方程(Modified Yule-Walker Equations,MYWE)和最小二乘法尤尔-沃克(Least Squares Yule-Walker,LSYW)方法，这些方法为ARMA频谱估计提供了相似的结果。

目前，贝叶斯推理已经成功地用于实际问题中。在贝叶斯推理中，未知参数被认为是一个随机变量[5]，因此假设与先验相关联的概率分布是从过去的数据或专家意见中指定的[6]。文中的主要目标是证明贝叶斯方法估计参数ARMA过程的可行性，通过比较ARMA模型参数的估计值和功率谱的估计值[7-8]，对经典估计方法和贝叶斯估计方法进行了比较。由简单的蒙特卡罗模拟MCMC算法得到了参数的平均估计值及其各自的标准偏差。

1 ARMA光谱模型

考虑阶数为(p,q)的ARMA平稳随机过程，由以下差分方程式定义：

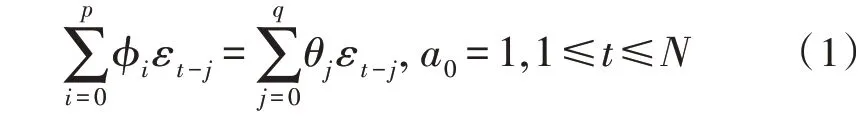
其中，i=0,1,…,p;j=0,1,…,q是过程参数，εt是均值为零、方差为2的白噪声。因此，要估计的参数向量为：

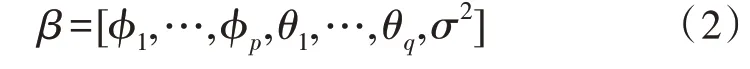
系统函数在z平面上定义ARMA过程的功率谱密度为：

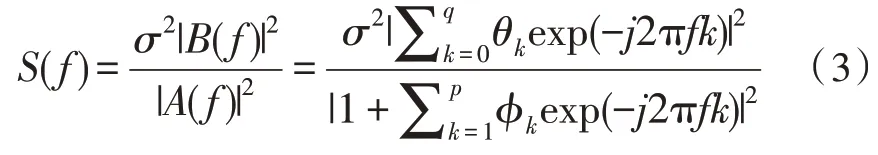
函数S(f)是自相关函数的傅里叶变换，估计频率有非负周期性，周期为1 Hz，频带限制在±0.5 Hz。

ARMA光谱估计的问题首先在于选择合适的模型，以便可以估计过程参数的向量，然后将估计值替换到光谱密度函数中。函数S(f)的这种参数化是通过使用参数β的向量实现的。

2 使用尤尔-沃克方程的估计方法

在使用修正的尤尔-沃克方程(MYWE)和最小二乘尤尔-沃克(LSYWS)时，在参数估计中使用了多于p个线性方程。在两种方法中，都可以对误差进行加权以稳定方差。此外，这些方法为ARMA频谱估计提供了相似的结果。

2.1 最小二乘尤尔-沃克方法

最小二乘尤尔-沃克方法旨在减少MYWE估计量的方差，提高估计量的质量。已知ARMA过程的自相关函数定义为：

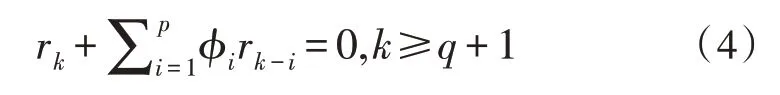
从MYWE出发，首先描述了改进的尤尔-沃克方程的最小二乘法，用于估计AR过程的参数，因为ARMA过程的尤尔-沃克扩展方程可以表示为r=-RΦ。其中，R是展开的自相关矩阵，r是自相关向量，可以获得AR矢量参数Φ=[φ1,…φp]T的一致估计。当M-q＞p时，方程式个数多于未知数个数，有解。为了估计自相关参数，应引入一个大小为(M-q)×1的误差e，公式为=-Φ+e。其中，和分别对应于r和R的估计量。

使用无偏自相关rk来估计r和R是很方便的，使近似误差的偏差为零。因此，可以使用最小二乘法来找到使误差平方和最小的向量，即由此可得，。

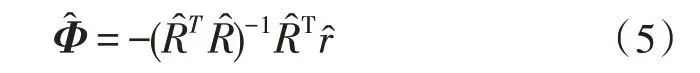
2.2 MA估计中使用AR滤波器的方法

新的分离估计方法包括利用Durbin方法的MA参数估计[9-10]对信号xt进行新的AR滤波，从而确定一个新的信号，如图1所示，表达式为。

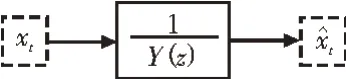
图1 AR滤波器滤波

在图1中，1/Y(z)是系统传递函数，并且，此过程类似于重复Durbin方法的第二步，这是独立估算方法的关键思想。

已知，AR(∞)过程可以作为MA过程的一种方法。在该方法中，使用新的信号估计值xt通过LSYW方法获得新的AR估计值，然后通过Durbin方法确定新的MA估计值[11]。提出方法的关键思想是从AR滤波中得到一个新信号，当ARMA过程的参数被重新估计时，它将提供更好的估计。

3 贝叶斯估计

在贝叶斯框架中，推理是基于参数β的后验分布，表示为p(β|x)，进而用于涉及到决策的推理和决策。后验分布p(β|x)是从先验分布f(β)提供的信息和数据通过似然L(β|x)提供的信息组合中得到的。因此，利用贝叶斯定理，给出了后验分布：

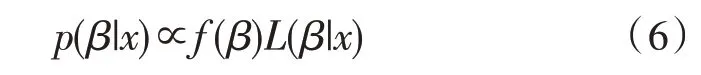
先验分布表示实验运行前有关参数β的不确定状态，后验分布描述观察到数据x后对参数β的更新信息。

对于一个ARMA(p，q)模型，需要估计参数β和σ，其中β=(φ1,…,φp,θ1,…,θq)。在给定矢量参数(β，σ)的情况下，针对观察值X的似然函数可以写成：

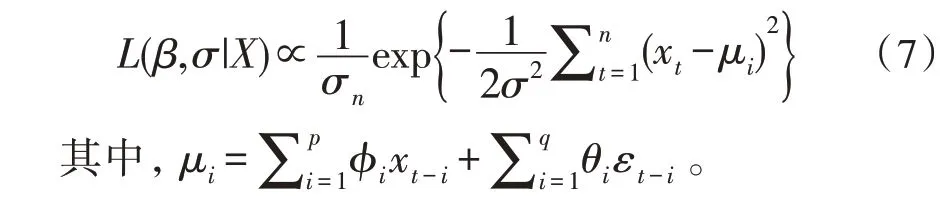
上述似然结合先验分布，得到的后验分布为：

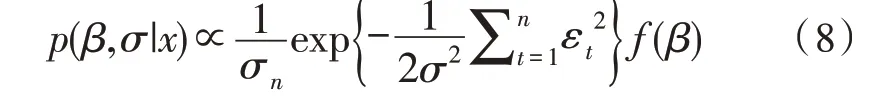
对于变量xi-p，i=1,2,…,p，误差项为εi-q，i=1,2,…,q。

为了进一步进行贝叶斯分析，有必要在参数空间上指定先验分布。根据所有当前可用的信息，可以使用不同的先验分布。如果研究参数的先验信息不可用或不存在[12-14]，则初始参数的不确定性可以用非信息先验分布来量化。因此，对于ARMA系数，可以将均匀分布用作先验分布。假设一个先验条件，即β的分量是独立的，则β的总体先验是其组件的先验乘积。因此，β和σ2的联合先验分布具有以下形式：

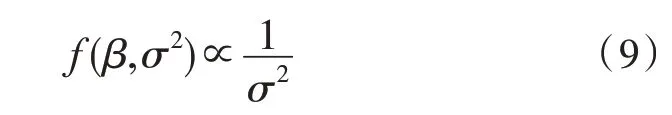
其中，-∞<β<∞和0<σ2<∞。

也可以考虑其他先验规范作为β分量的独立信息正态分布，即βj～N(μ,),j=1,…,k，均值μ和方差指定了信息先验作为参数σ2的逆Gamma分布，即σ2～IG(aσ,bσ)的超参数aσ和bσ已知。因此，β和σ2的联合先验将为f(β,σ2)∝f(β)f(σ2)。

为了从模型中获得每个参数的边际后验分布，需要解决涉及联合后验密度的积分，这些积分在解析上不易处理，并且标准积分逼近的效果不佳。在这种情况下，使用马尔可夫链蒙特卡罗(MCMC)方法进行贝叶斯后验推理。具体而言，可以运行一种算法来模拟从后验分布中提取的长链，并基于从样本中计算出的参数或参数函数的后验总结进行推断。MCMC本质上是使用马尔可夫链的蒙特卡罗积分。

假设在时间t处，首先从提议分布q(η|γt)中对候选点η进行采样来选择γt+1，接受候选η的概率为：

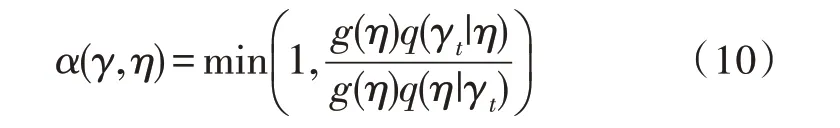
如果候选点被接受，则下一状态变为γt+1=η。如果拒绝，则γt+1=γt且链条不移动。从MCMC算法获取β每个分量的随机样本后，重要的是研究诸如收敛和混合等问题，以确定该样本是否可以被合理地视为目标后验分布的一组随机实现。除了正式程序外，查看边际迹线图是检查输出的最简单方法。这样，链的所有值都具有由均衡分布给出的边际分布。

4 数值图示

下面描述蒙特卡罗模拟，以便获得与每个ARMA流程相对应的参数和频谱功率密度的估计。仿真和程序在Matlab中实现。

模拟中使用的方法是改进的尤尔-沃克方程MYWE、最小二乘改进的尤尔-沃克方程(LSYW)、具有AR滤波的最小二乘尤尔-沃克方程(LSYWSAR)、最大似然估计器(MLE)、考虑非信息先验和独立正态先验参数的贝叶斯估计器。

为了评估这些方法的性能，从相同的种子中生成随机数据，并随序列的变化而变化，i=1,…,B,B是每次模拟中的重复次数。使用N=256个观测值和B=30次重复进行此操作。从均值等于零且方差等于1的标准高斯分布(白噪声)生成随机数，然后生成过程ARMA的信号。

改进的协方差是Durbin方法的标准，选择较大的AR过程阶数，并根据要分析的光谱特征选择了方程数M。另一方面，对于极点远离单位圆的频谱，M取一个小数，它的一个极点靠近单位圆，另一极点远离单位圆。

在第一个示例中，使用ARMA(4,2)模型，其中M=10，L=85，N=256；在第二个示例中，使用ARMA(4,4)模型，其中M=20，L=125,N=256。

示例1 ARMA(4,2)模型

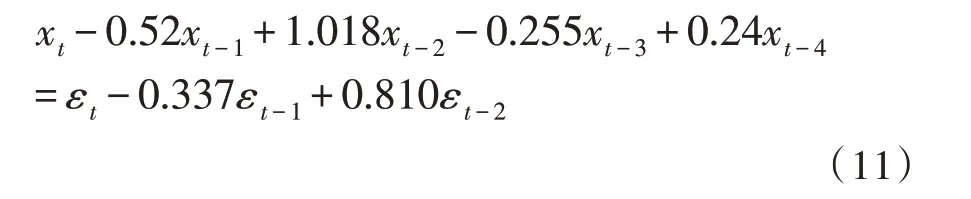
示例2 ARMA(4,4)模型

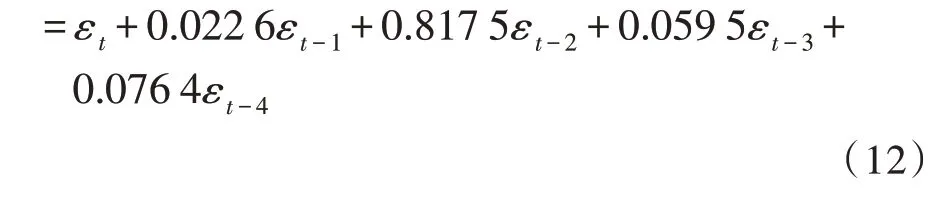
首先，利用示例1的数据拟合ARMA(4,2)模型，对经典方法进行比较分析，LSYWS方法相比其他方法提供了估计参数的最佳平均值，但与AR模型的LSYW方法相比，变异性稍大。LSYW方法产生中间估计值，但性能优于MYWE和MLE方法。这些事实可以通过图2(a)～2(d)中频谱功率的平均估计来观察，这表明LSYWS方法提供了最佳估计。将文中研究的经典贝叶斯方法与非信息性先验贝叶斯方法进行比较发现，两种贝叶斯方法的参数估计值均与LSYWS方法相似，但变异性较小(参见图2(e)、2(f))。图2中，虚线是理论值，实线是估计值的平均值。

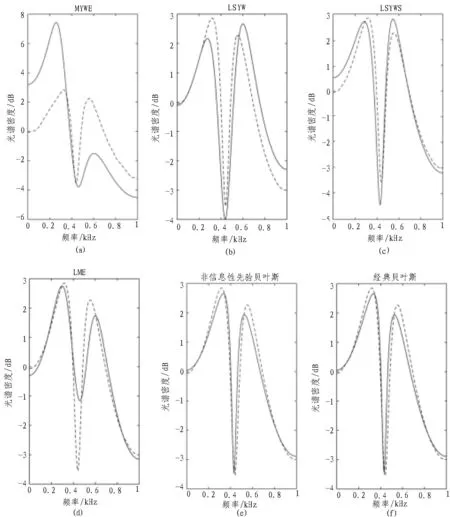
图2 光谱密度与频率之间的关系(ARMA(4,2)模型)

通过使用非信息性先验，获得了比经典先验算法更好的估计，这是由于LME给出的平均先验不能产生如此好的结果。应用于ARMA(4,4)模型的估计方法MEYW、LSYW、LSYWS和MLE的结果见图3。在这种情况下，所有考虑方法的参数平均估计值近似相等，只是平均估计值的标准偏差显示出与贝叶斯标准偏差之间的差异[15-16]。非信息性先验下的标准差比其他方法的值小，但略小于MLE法得到的标准差，该分析还可以通过功率谱估计值的曲线来确认。在这种情况下，这种相似性可能是由于ARMA(4,4)具有稳定的功率谱，并且比以前的情况要估计更多的参数。

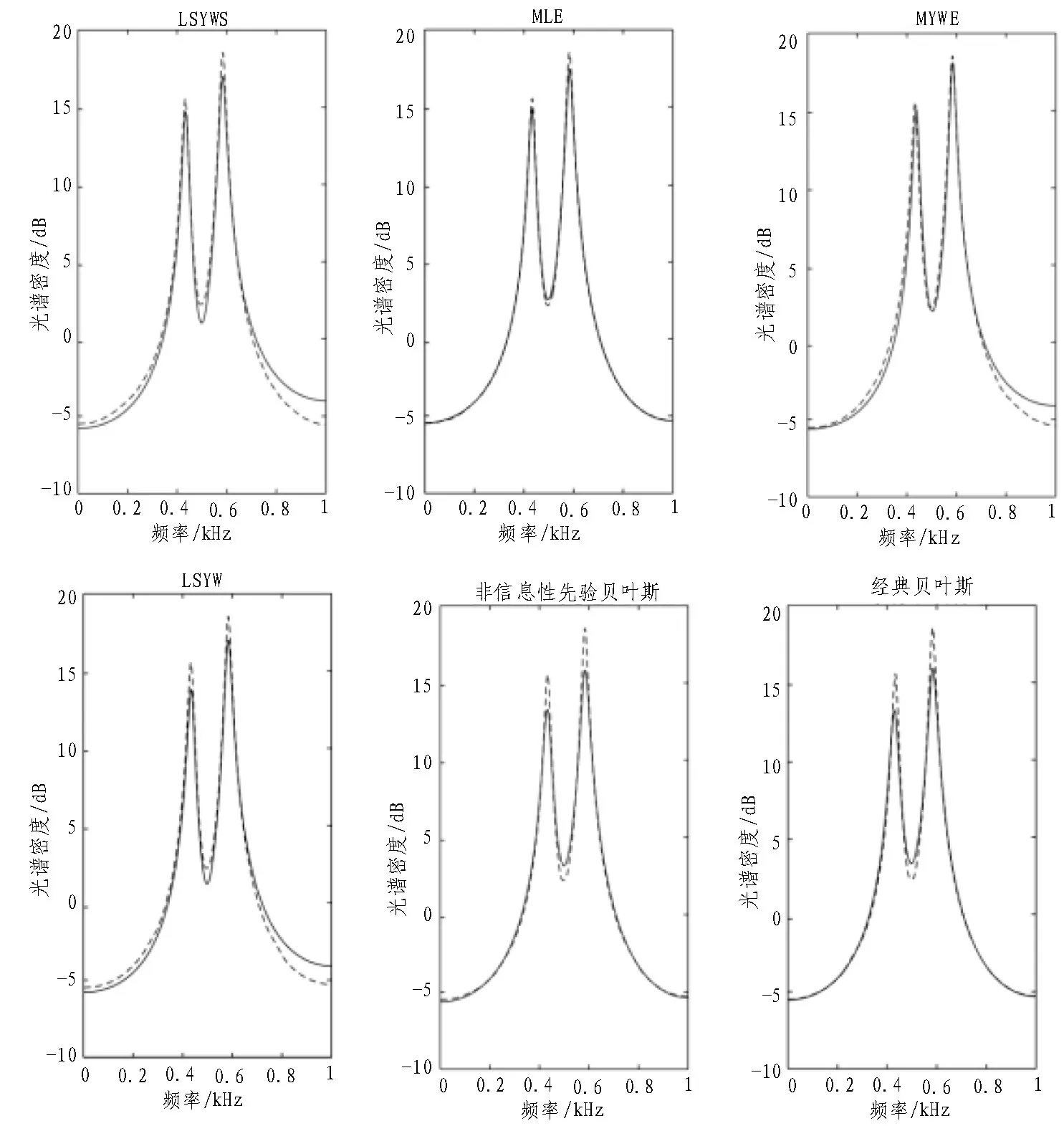
图3 光谱密度与频率之间的关系(ARMA(4,4)模型)

5 结论

文中通过使用非信息先验分布估计ARMA模型的密度谱来描述贝叶斯方法[17-18]。将该贝叶斯方法与非贝叶斯方法——LSYWS方法和LSYW进行了比较，二者均基于尤尔-沃克方程。引入了两个具有不同顺序的ARMA模型，以说明所建议的方法并检查其性能。该研究表明，考虑ARMA(4,2)模型，贝叶斯方法比其他方法产生的估计值更准确。对于不太稳定的ARMA模型，贝叶斯方法是合理的，并且可以选择任何一种方法来获得更稳定的功率谱。与其他方法相比，贝叶斯方法提供了适用于任意阶次ARMA模型的光谱的最佳拟合。