Modeling Dysentery Diarrhea Using Statistical Period Prevalence
2021-08-26FouadAbolaban
Fouad A.Abolaban
Department of Nuclear Engineering,College of Engineering,King Abdulaziz University,Jeddah,21589,Saudi Arabia
ABSTRACT Various epidemics have occurred throughout history,which has led to the investigation and understanding of their transmission dynamics.As a result,non-local operators are used for mathematical modeling in this study.Therefore,this research focuses on developing a dysentery diarrhea model with the use of a fractional operator using a one-parameter Mittag–Leffler kernel.The model consists of three classes of the human population,whereas the fourth one belongs to the pathogen population.The model carefully deals with the dimensional homogeneity among the parameters and the fractional operator.In addition,the model was validated by fitting the actual number of dysentery diarrhea infected cases covering 52 weeks in 2017,which occurred in Ethiopia.The biological parameters were fitted,and fractional order ν was optimized.The basic reproduction numbers R0 were 1.7031 and 1.9581,which correspond to the fractional and integer-order models,respectively.The fractional model showed smaller discrepancies compared to the integer-order model when the models were fitted and validated with the actual cases of infected humans.Qualitative theory for the existence and uniqueness of the solutions was extensively explored,and the stability of equilibria was investigated.The most influential parameters were found via forward sensitivity indices.This multidisciplinary research shows and explains the results of numerical simulations applied to a biological issue.
KEYWORDS Dysentery diarrhea model;Mittag–Leffler kernel;fractional operator
1 Introduction
The literature provides mathematical models for the transmission of infectious diseases.These models play a significant role in quantifying and evaluating the effective control and preventive measures of infectious diseases[1–3].Furthermore,mathematical modeling has been used in several ways as a versatile and effective way of studying the dynamics of infectious disease transmission.This can include the classic susceptible,infected,and recovered(SIR)model or more advanced models[4].Mathematical analysis and numerical simulations can be collectively used for the development and evaluation of persuasive control measures.
It is popularly known that mathematical models can predict the emergence of infectious diseases and epidemics,which are beneficial for public health planning and initiatives.By using compartmental models as a simple mathematical structure,the complex dynamics of epidemiological processes can be examined[5].These compartmental models divide the population into two distinct health categories.The first category is depicted byS,and involves those susceptible to pathogen infection,while the second,denoted by I,involves the pathogen-infected humans.The manner in which these two populations interact is based on phenomenological assumptions used to develop the models.Ordinary differential equations(ODEs)are typically used to develop these models.
Additionally,other populations denoted by R,which is the image of the immune/removed/recovered compartment,are considered to make these models more practical.A significant challenge here is to obtain sufficient parameters for a particular disease,which would determine the factors affecting potential control measures,such as medication or vaccination.The crucial question is about the execution of such measures from an optimal viewpoint.Several notable attempts have recently been made to introduce this research program for various diseases with integer compartmental models[6–11].
Over the past few decades,many scientists have shown that fractional models can effectively represent natural phenomena compared to integer-order differential equations.Therefore,fractional calculus has gained more importance and popularity for modeling realistic cases,especially memory effects[12–14].Due to this particular function,various fractional operators have been developed to accurately model the memory effects of various types of diseases[15–22].Nevertheless,further research is required to explain such complex dynamics.Classical fractional models with singular operators cannot effectively model the non-locality of real-world applications.To overcome this challenge,we investigated and examined a new fractional version of an epidemiological model for the dysentery diarrhea involving the ABC operator,known to have a non-singular kernel with memory effects.
2 Formulation of the Dysentery Diarrhea System
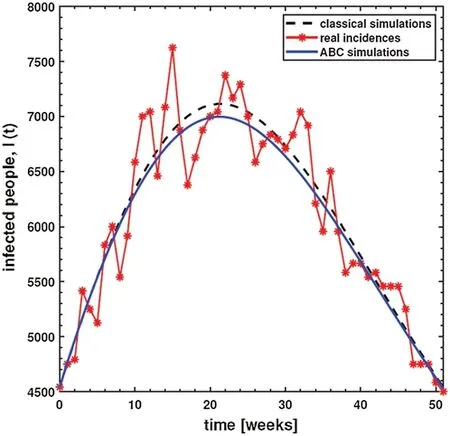
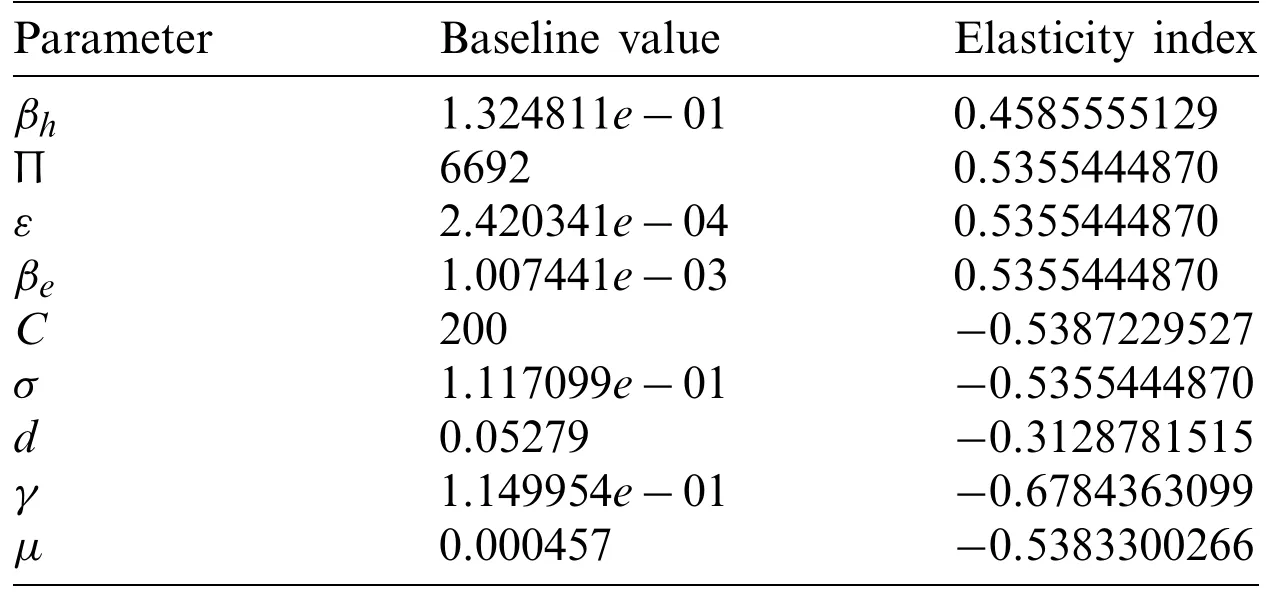
This section demonstrates the formulation of the dysentery diarrhea disease in terms of a deterministic model based on a nonlinear system of ODEs over a finite time interval[0,T],0 The model is designed based on the following assumptions: •Transmission of the dysentery diarrhea disease occurs through multiple pathways. •There is a homogeneously mixed population •Π is the rate of recruitment of those susceptible either by birth or immigration •Standard incidence is assumed in the human to human interaction •Logistic phenomenon is taken into consideration in the human to environment interaction,which is represented below: whereCstands for theShigellaconcentration that causes a 25% likelihood of getting the disease •βhandβestand for rates of ingestingShigellafrom human to human interaction and through a contaminated environment,respectively.βh=ap(a= contact rate andp= probability of disease transmission per contact) •After losing immunity,individuals return toS(t)at a rate ofα •Infected individuals cause concentration ofShigellaat a rate ofε •Shigellapopulation dies at a rate ofσ •Rate of recovery of infected humans isγ •Natural mortality rate of humans isμwhere death due to dysentery diarrhea disease occurs at a rate ofd •Non-negativity is assumed for all biological parameters introduced within the model Hence,after incorporating all the above assumptions and considering the Atangana–Baleanu differential operator taken in the Caputo sense[15],we have obtained the following coupled nonlinear system of ordinary differential equations: subject to the following initial conditions: S(0)=S0≥0,I(0)=I0≥0,R(0)=R0≥0,B(0)=B0≥0, We then obtain: where, The kernels in Eq.(5)satisfy the Lipschitz condition for 0 ≤Mi<0,i=1,2,···4.WhenS(t)andS∗(t)are two functions,we get: whereM1=(Πh+ΠB+μν). Thus, Repeating the same procedure above,yields: Subsequently,Eq.(4)gives: whereS(t)≥0,I(t)≥0,R(t)≥0,B(t)≥0.The difference between successive components can be denoted byrespectively.Thus in view of Eqs.(7)–(9),we obtain: Theorem 3.1The fractional proposed model possesses a unique solution for t∈[0,T]if the condition is satisfied Proof.Based on the assumptions thatS(t),E(t),Q(t),IA(t),IS(t),R(t)are bounded functions,it is therefore clear that the kernelsF1,F2,F3,F4,F5,F6from Eqs.(7)–(8)satisfy the Lipschitz condition.Hence,Eq.(10)can be viewed as: Hence,the sequences above exist asAlso,using the triangular inequality for anykvalue,Eq.(12)yields: For the validation of an epidemiological model,it is extremely important to compare the results of simulations with the actual data of infected individuals.This increases the reliability of the proposed disease model.Similar values from the simulations and actual data give better information on the disease being investigated.In addition,unknown values of the working parameters that contribute to the model can be determined. There are different techniques including maximum likelihood estimation,Bayesian technique,nonlinear least-squares approach,and probability plotting,which can be used to obtain the best parameters.In this research,we utilized the nonlinear least-squares approach for computing the best-fitted parameters,including Π,βh,βe,d,ν,ε,andσ,along with the most important parameter of our proposed model,called the fractional orderν(one of the major components of the study).We also obtained the best-fitted parameters for the classical dysentery system and ABC fractional dysentery system,which are shown in Tab.1.The actual data for the dysentery diarrhea infected individuals was from Ethiopia,which covered a period of 52 weeks in 2017[26]. Table 1:Best fitted and constant parameters for classical(ν=1)and ABC(ν/=1)versions of the model When the least-squares technique is utilized,we need to minimize the objective function.This is achieved by tuning the system’s parameters to fit the available data points accurately.Real data cases for the dysentery diarrhea disease in this study are denoted bympoints(xn,yn),n=1,...,m,wherexnstands for independent quantity andynshows dependent quantity.The system function has the structureh(x,r),wherestuned parameters are shown in a vector of parameters,r.Hence,the objective is to identify the parameters which ensure that the system’s simulations for the infected cases fit well with the actual data points. In the present study,we obtained the best fit by measuring the difference between the real data and the simulations.This is shown below: Finally,the optimal set of parameters is obtained,as shown in Tab.1,with the least-squares approach while minimizing the absolute relative error,on average,as shown below: whereNstands for the total data value,which is 52 in this study.Moreover,real prevalent cases of the dysentery diarrhea disease,along with the classical and the ABC system’s simulations for the infected individuals,are listed in Tab.2.In addition,Fig.1 shows the best fit of the classical and ABC system with the real cases.The ABC system showed an average absolute relative error of 3.4284e−02,and the classical system was 3.4432e−02.Therefore,it shows that the ABC system had some advantages compared to the classical dysentery diarrhea system.In addition,the basic reproductive numberswere 1.7031 and 1.9581 for the ABC and classical systems,respectively.This clearly shows that the disease can be well prevented if the ABC operator is taken into consideration while modeling the epidemic. Table 2:Dysentery diarrhea cases for 52 weeks in 2017 from Ethiopia[23]:First,second and third rows stand for real cases,classical simulations and ABC simulations,respectively Figure 1:Plots and comparison of the real incidence cases,classical(ν = 1)and ABC(ν =9.9410e−01)systems for the dysentery diarrhea The numerical values indicating the relative significance ofR0are given in Tab.3.Some parameters are positive while some are negative.Parameters with positive values mean that an increase in the parameter’s values will have a major effect on the frequency of the ailment spread.On the other hand,parameters with negative values mean an increase in such parameters would decrease the effect of the disease.A representation of the values given in Tab.3,is shown in Fig.2. Table 3:The baseline values and elasticity indices for different model parameters(2)[R0 =1.703052076] Figure 2:Elasticity indices for various parameters of 0 In this section,an algorithm is first developed to obtain the approximate solution of the ABC dysentery diarrhea model,wherein the operator uses non-local and non-singular types of the kernel.The algorithm being developed is discussed in[28],which entails the combination of the fundamental theorem of fractional calculus and two-step Lagrange type polynomial.Therefore,the fundamental theorem of fractional calculus on the Cauchy type initial value problem is given below: This leads to: Att=tn+1,n=0,1,2,...,we have: With the help of interpolation polynomial,we approximate functionG(τ,w(τ))over[tv,tv+1]: Eq.(24)becomes: By solving the above integrals,we obtain the approximate solution shown below: Hence,the proposed dysentery diarrhea model becomes: where, Using numerical simulations,the ABC dysentery diarrhea model(2)uses the developed algorithm shown above.Different values of the key parameters are chosen to investigate their effects on the dynamics of the disease.These parameter values are taken from Tab.1.With simulations,we can identify important parameters that significantly affect the model’s dynamics.In order to investigate the transmission rate of dysentery due to human to human interaction(βh)and environment to human interaction(βe),we vary both parameters,as shown in Fig.3. Figure 3:Behavior of diarrhea infected people with increasing values of(a)effective transmission rate of dysentery due to human to human interaction(βh)and(b)effective transmission rate of dysentery due to the environment to human interaction(βe),while taking the remaining parameters from Tab.1 This shows that diarrhea disease is principally due to the environment to human interaction.It means that humans must take care of their hygiene and surroundings in order to avoid the spread of dysentery.In order to investigate the effect of the concentration ofShigellapathogen(C)and the net death rate ofShigellapathogen(σ),we have varied both parameters,as shown in Fig.4.This demonstrates that decreasing the values of the net death ofShigellapathogen leads to a reduction in the infection,while its concentration(C)follows the same pattern as the normal curve. Figure 4:Behavior of diarrhea infected people with increasing values of(a)concentration of Shigella pathogen(C),and(b)net death rate of Shigella pathogen(σ),while taking the remaining parameters from Tab.1 In order to investigate the effect of the pathogen shedding rate of infected humans(ε)and the recovery rate of dysentery(γ),we have varied both parameters,as shown in Fig.5.This demonstrates that increasing the values ofεcauses the infection rate to rise.This is because its shedding rate on humans also increases,whereas a slight improvement in the recovery rate decreases the infection rate substantially. Figure 5:Behavior of diarrhea infected people with increasing values of(a)pathogen shedding rate of infected humans(ε)and(b)recovery rate of dysentery(γ),while taking the remaining parameters from Tab.1 Finally,in order to investigate the effects of different parameters on the basic reproductive number,0,we have presented various contour plots,as shown in Fig.6.This shows that dysentery diarrhea can be prevented effectively if some strategies,including environment to human interaction,the concentration ofShigellapathogen,and pathogen shedding rate,are carefully considered. Figure 6:Behavior of basic reproductive number,0 under the influence of different parameters of the proposed ABC system(2) In the present research,one of the robust non-local and non-singular fractional operator,called Atangana-Baleanu,was used to model dysentery diarrhea.The employed fractional operator was suitable for the investigation of transmission dynamics of a disease from the literature.The fractionalized order isν,and the dimensional consistency between the rest of the parameters has been considered.Consequently,several important features of the proposed fractional variant of the model,such as the formation of the model,existence and uniqueness of the solution by means of fixed point theorem,stability analysis,sensitivity analysis and most importantly,the estimation of the parameters have been reported.It was observed that the fractional variant of the model represents the behavior of the ailment more accurately than the integer-order variant.The dimensional homogeneity among parameters and the ABC operator have been authenticated by fitting the dysentery diarrhea infected cases from Ethiopia covering a period of 52 weeks in 2017.In addition,the ABC operator’s fractional order,νwas optimized.This returns a basic reproduction number,0of 1.7031 and0of 1.9581,for the integer model.It is shown that the ABC model has smaller values than the integer-order,whereas the proposed models match the actual cases of infected humans. Furthermore,in order to shed more light on the features of the model,various numerical simulations were carried out using an effective numerical scheme.In future studies,we plan to apply the techniques used in[29–34]to understand dysentery diarrhea dynamics in greater detail.In addition,optimal control theory will be utilized to devise effective control strategies to eliminate the epidemic. Acknowledgement:This project was funded by the Deanship of Scientific Research(DSR)at King Abdulaziz University,Jeddah,under Grant No.RG-6-135-40.The authors,therefore,gratefully acknowledge DSR technical and financial support. Funding Statement:This research is supported by the King Abdulaziz University RG-6-135-40. Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
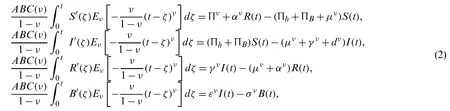
3 Existence and Uniqueness




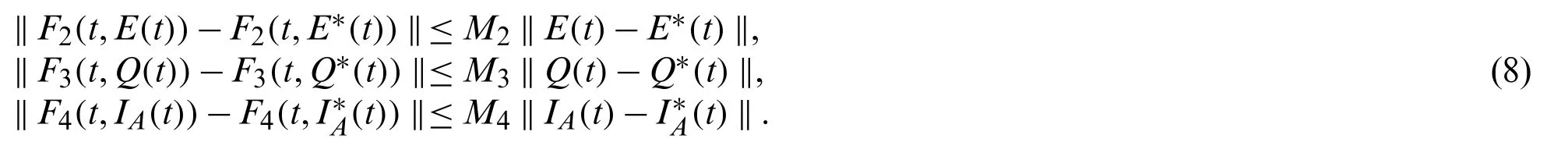

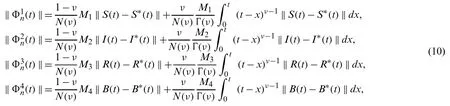



4 Stability and Basic Reproductive Number

4.1 Global Stability of the Ailment-Free Equilibrium

5 Parameters Estimation




6 Sensitivity



7 Simulations for the ABC Model





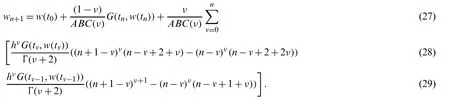
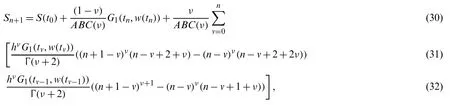






8 Conclusion
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- Monte Carlo Simulation of Fractures Using Isogeometric Boundary Element Methods Based on POD-RBF
- A Pseudo-Spectral Scheme for Systems of Two-Point Boundary Value Problems with Leftand Right Sided Fractional Derivatives and Related Integral Equations
- A Numerical Model for Simulating Two-Phase Flow with Adaptive Mesh Refinement
- Variable Importance Measure System Based on Advanced Random Forest
- Parameters Calibration of the Combined Hardening Rule through Inverse Analysis for Nylock Nut Folding Simulation
- Optimal Control of Slurry Pressure during Shield Tunnelling Based on Random Forest and Particle Swarm Optimization
