林之博，刘媛华

(上海理工大学 管理学院，上海 200093)

1 引 言

复杂连续函数极值问题是一类常见的优化难题，对特定的复杂函数，通常可以通过求导的方法找出精确极值解.但实际情况中存在维度较高、求解域广泛、全局最优解在微搜索域褶皱中难以定位的复杂函数，精确求解方法往往无效，只能用启发式算法尝试求出满意解.目前有学者提出改进混合粒子群算法[1]，针对特定工程应用问题有一定的效果；另有研究使用改进的水波优化求解优化问题，在水波优化算法基础上融合了单纯型法和简单Logistic混沌特性，能够有限提升算法性能[2]；此外常见的优化过的遗传算法、蚁群算法、粒子群算法等也具有求解中等复杂连续函数极值的能力，但收敛时间容易过长[3].上述算法虽能对某些问题取得较好求解效果，但普遍容易陷入局部最优后无法跳出.

混沌优化算法最早是由李兵等人于1997年提出的一类智能优化算法[4]，该算法理论上具有很强的跳出能力，可以规避蚁群算法、遗传算法等陷入局部最优无法跳出的情况[4].通常在该算法中引入Logistic混沌系统[5，6]，利用混沌映射的遍历性、初值敏感性等特征产生混沌序列作为搜索最优解的轨道[1，4].沿该轨道对解空间进行搜索，有更大的可能性找到目标最优解[4，6].混沌优化算法自提出后常被用于结合改善其他算法，例如结合混沌系统构成新型混沌粒子群算法[1]、混沌鲸鱼算法[5]、以及混沌烟花算法[7]用于解决多维复杂单目标连续函数极值问题.

虽然现有混沌优化算法具有较好跳出局优的能力，但Logistic系统模型在数据仿真实验中展现出明显的过度边缘游走现象[8]，导致同等算力下算法对解空间中心区域的搜索过于稀疏，落入局部最优可能增大，在李金屏等人的仿真测试结果[8]中可得到佐证.故以Logistic为混沌内核的算法往往带有这类特性.王德成等人改进了Logistic混沌[9]，利用反三角Logistic映射产生混沌轨道，以达到等概率搜索的目的，但经过点分布检测仿真实验发现其均匀度鲁棒性欠佳，且算法不均衡，收敛性较弱；官国荣等人提出的改进Lorenz系统所得新模型能够产生更复杂的混沌行为[10]，但轨道形状难以规范到指定区间.此外，原始的混沌优化算法和基于随机过程的智能进化算法容易落入微搜索域褶皱上的局部最优值，典型例子是在解决高维Griewank函数极值优化问题时，很难找出全局最优，在解决“大海捞针问题”一类函数时也非常容易落入包围式局部极值点，通常增加混沌轨道长度能缓解该问题，但会导致混沌轨道过于密集，浪费计算能力的同时也造成了运算时间增长[11].

故考虑改进设计一种新的混沌映射系统，使得混沌轨道均匀度与鲁棒性尽可能高；同时，基于新模型设计一套混沌优化算法，一定程度上增强跳出局部最优的能力并提高算法收敛效率.对新模型进行混沌分布检测和算例测试对比，以证明该算法具有更好的优化性能[11].

2 模型性质与改进

2.1 混沌系统性质

混沌系统是一类具有运动状态长期不可预测且对系统初始状态极端敏感的动力系统[4].这类系统一般由状态参量与控制参量共同组成，其中状态参量表示系统在状态空间里的运动过程中所处的位置[12]；而控制参量可对系统的运行状态产生显著影响.从某一时刻的初始系统状态出发，使系统按照混沌方程式进行演化，产生的轨迹局部上完全杂乱无章，但全局来看却具有其规律性(例如Lorenz混沌)[13].混沌系统常被应用于通信加密、工程控制领域，根据不同需求可用特定手段产生或消减混沌.所有混沌系统运动普遍具有共同特征，此处对研究所需的几种性质做出简单描述.

性质1.混沌系统具有初值敏感性[4].对任意一个混沌系统的初始条件给予极其轻微的扰动，都可以造成系统运行轨迹完全改变.例如Logistic混沌系统中，给予初始Xn大小为10-6的扰动，可导致系统运动到n=24时，整体偏离值达到0.8719.因此，在优化领域可利用该性质产生长度相等但差异巨大的序列用于生成搜索轨道，即待优化函数的可行解集[6].

性质2.混沌系统具有随机性，即任何混沌系统状态的改变长期难以预测，近乎随机[6].例如Lorenz混沌系统从吸引子某一叶上发生跳转的行为都是随机产生的，但这种随机行为发自系统非线性因素[14].该性质在合理增强后，有助于加快对解空间的均衡搜索.

性质3.混沌系统具有遍历性，只要给予足够长的时间，混沌系统能在某范围内永不重复地游走、经过该空间中所有的系统状态.利用该性质有助于规避局部最优[9].

性质4.对于混沌动力学系统，其Lyapunove指数与轨道或其等效的映射的表示形式无关[15].即对于线性变换，Lyapunove指数不会发生变化，也不会改变系统的混沌行为.因此对混沌轨道进行缩放操作不改变系统混沌特性[16，17].

2.2 改进混沌系统

原Logistic混沌的方程式如式(1)所示[4，6]，其中X为状态参量，μ为控制参量，当μ取值为4时，系统进入完全混沌态；式(2)为王德成等人提出的反三角变换方程式[9].

Xn+1=μXn(1-Xn)

(1)

(2)

对原Logistic混沌与反三角Logistic系统进行对照分析检验.利用Logistic、反三角Logistic混沌系统各产生两条长度为1000的序列，归一化到[0，1]区间构成XOY上的分布.设XOY面上混沌区域中心为(x0，y0)，计算从中心开始逐步等面积间隔扩大统计范围对应的横纵坐标增量，公式如下：

(3)

其中，UpB为坐标轴上限，DownB为坐标轴下限.分别统计轨道上落在公式(4)所示区间上的点数，记为序列Counter.

(4)

若一个混沌系统轨道分布均匀度较高，则Counter曲线线性表现越明显.计算Counter中所有元素间差值C[k]-C[k-1]，记为E序列.则混沌轨道均匀度可通过公式(5)计算：

(5)

依该方法计算得出原混沌优化中Logistic模型、反三角函数Logistic混沌轨道分布均匀度指标如表1所示.

表1 Logistic与反三角Logistic混沌100次采样均匀度对比

作出两个混沌系统的Counter序列曲线与混沌分布对比如图1所示，图1(c)所示Logistic混沌边缘搜索导致的Counter曲线指数型上翘；而图1(b)展示的反三角Logistic混沌比图1(a)所示Logistic混沌分布更加均匀，结合图1(d)和表1可见反三角函数Logistic混沌系统均匀度确实优于原Logistic混沌，但该混沌系统均匀度并不稳定，时大时小，鲁棒性欠佳.

图1 混沌分布与Counter曲线对照

为了更好地避免引入Logistic边缘游走效应的影响、并提高混沌轨道均匀度鲁棒性，考虑基于Lorenz混沌系统改进设计新混沌模型.Lorenz混沌是Lorenz于1963年研究天气演化时提出的简化描述方程，其模型[10]如式(6)-式(8)所示.其中，Xn+1、Yn+1、Zn+1都为Lorenz混沌系统的状态参量，a、b、c都是Lorenz混沌系统的控制参量，通常取a=10、b=28、c=8/3.Lorenz系统在空间中呈现蝴蝶翅膀形状的两个混沌吸引子，因此又被称为“蝴蝶混沌”[10].

Xn+1=Xn+a·(Yn-Xn)·Δs

(6)

Yn+1=Yn+(b·Xn-Xn·Zn-Yn)·Δs

(7)

Zn+1=Zn+(Xn·Yn-c·Zn)·Δs

(8)

由于该系统具有不同于Logistic离散系统的连续混沌特性，在状态空间中进行更均匀的遍历，故减少类似Logistic系统边缘游走的效果更加良好.

对系统产生的Z轴序列做模运算和信号变换操作如公式(9)所示，可获得分布较均匀的混沌轨道Zsn+1，并规避细微扰动时混沌轨道间偏移过小的情况.

Zsn+1=Zn+1·IMODGear

(9)

I为信号放大控制参量，不妨取15或16；Gear用于调控序列分片模式，当Gear=10或Gear=10I时，轨道都会丧失随机，经仿真实验认为取Gear=10I/3时效果最佳.

使用公式(3)-公式(5)计算改进模型的分布均匀度如表2所示，其二维分布如图2所示.可知改进后模型相对反三角Logistic混沌系统模型产生的混沌轨道具有更高的分布均匀度和更好的鲁棒性.

表2 分片Lorenz混沌100次采样均匀度

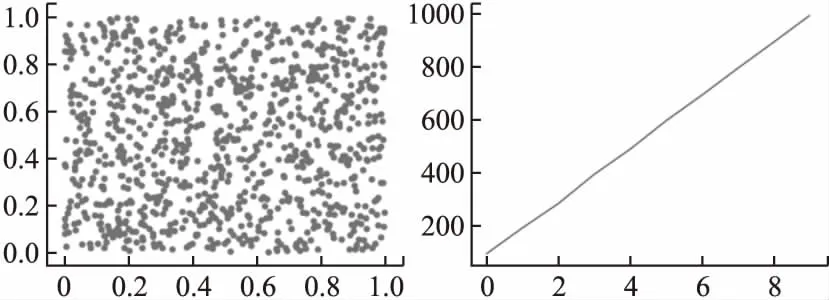
图2 改进Lorenz混沌分布与Counter曲线对照

故根据性质2，理论上基于新设计的混沌系统模型开发新型混沌优化算法会具有更高的搜索效率.为便于描述，后文统一将基于改进模型的新型算法简称为“MLC”算法.

3 算法设计

3.1 MLC搜索算法框架

设计MLC算法总体框架如图3所示，算法由4项子算法、载波控制器、混沌扰动模块和停机控制器构成.

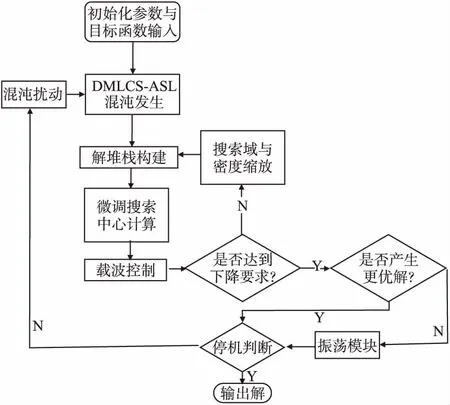
图3 算法总框架

算法开始需设定初始化参数，例如混沌系统状态参量和初始可行解等，并指定待优化目标函数和优化方向.开始子迭代过程，运行混沌发生子算法，由性质1：基于2.2设计的改进模型通过随机微小扰动可产生规定大小的均匀混沌搜索轨道(即可行解集).将产生的轨道输入到解堆栈子算法中，构造解堆栈；由性质3可知当轨道足够长或扰动次数足够多时，堆栈中一定包含满意解.将堆栈放入聚集出栈子算法，根据堆栈中的解计算搜索中心.

对于新产生的搜索中心，使用载波控制器计算当前解下降是否达到目标精度；若未达到，运行搜索域密度缩放子算法缩小搜索的区域和搜索密度后，转回混沌发生子算法继续进行该子迭代；否则，当子迭代产生更优解时，进入停机判断，若子迭代产生解非更优，则用振荡模块修改子迭代初始搜索上下限后再进入停机判断.

接下来对各项子算法给出详细描述.

3.2 混沌发生子算法

设F(X)为待优化目标函数，其中X={xi}为函数的i个变量；另有参数up、down分别表示由X中各个变量的区间上限和下限构成的向量；z0为混沌系统的初始Z取值；step为状态转移步长，研究过程中取值为0.01；times为设定混沌轨道总长；aband为混沌系统初始演化轨道上删去的长度，用于保证获得的混沌轨道完全处于混沌状态中，一般取100.设XLorenz(up，down，Z0，step，T，aband)为分片Lorenz混沌模型在第T次移动时产生的混沌Z轴值；取信号放大参量I=1016，分片参数Gear=105.混沌发生子过程如下：

Input：input={up，down，Z0，step，T，aband}；

Output：TrackMat；

Step 1.初始化Lorenz混沌状态参量X、Y、Z，设置a=10，b=28，c=8/3；设置系统初始空间位置为x=1，y=1，z=Z0；

Step 2.给予z=1一个10-4级别的随机扰动，按照给定的轨道长度T利用分片Lorenz混沌系统模型产生混沌轨道；

Step 3.若混沌轨道数量未达到待求解问题维度，返回Step 2；否则转到Step 4；

Step 4.使用最大最小映射法方法，将混沌轨道压缩到当前搜索域；

Step 5.将混沌轨道作为一个数据矩阵TrackMat输出.

该算法根据输入up、down序列的长度i产生和返回i个混沌序列构成的可行解集矩阵TrackMat；在输入变量中引入随机过程来增加算法的不确定性，每个变量对应的混沌序列是通过z加一个极小的随机数作为初值扰动后输入算法中得到的.故有产生更多完全不同的可行解集的能力，使算法得以多次进行泛化运行测试.

3.3 解堆栈子算法

解堆栈子算法可以最快的速度从TrackMat中确定一组逐渐逼近最优的解.该算法按照替代优化和渐进禁忌法则依次将混沌搜索轨道上找出的渐进优化解压入堆栈中，在子算法结束时栈顶元素必定为本次迭代搜索到的最优解.运算过程下：

输入：TrackMat，order；

输出：Solution；

Step 1.在搜索域中随机选取初始解向量，作为临时栈底解；

Step 2.按照顺序提取TrackMat中的解，并计算解值；

Step 3.比较该解和栈顶解，当order要求求解最大值时，若当前解对应解值比栈顶解解值大，则将该解压入栈中，否则抛弃；若order要求求解最小值时，若当前解对应解值比栈顶解解值小，则将该解压入栈中，否则抛弃；

Step 4.若轨道中所有解向量都被遍历到，转Step 5；否则转回Step 2；

Step 5.输出堆栈Solution；

算法在搜索域中随机生成临时栈底解，这一随机过程使得有多种解堆栈的可能性，由于混沌轨道解值完全随机排列，有很大可能在较早的搜索过程中就遇到较优解，使得渐进禁忌标准迅速逼近最优解值，从而缩减解堆栈的高度；替换优化过程则反复更替拟采用解，进一步逼近全局最优可能存在的域.通过解堆栈算法构造的堆栈一般情况规模较小，能减少出栈时的计算量.

3.4 聚集出栈子算法

在子迭代前期的大搜索域中取得解堆栈后，如果直接使用栈顶元素作为下次缩放搜索中心，有较大可能性导致最终收敛到局部最优解，尤其是类似于如图4所示SCHAFFER N.2函数微搜索域褶皱上的局部最优解.

图4 SCHAFFER N.2褶皱上的局部最优

因此设计聚集出栈子算法，在一定程度上，控制搜索中心在搜索域缩减到不可逆之前向适应度相近的其他邻域的方向偏移，并在搜索轨道运行到微搜索域时逐渐减少干涉，使落入局部最优的机会偏小.设Pk为堆栈Solution中第k行解向量，P0为栈底解，Pn-1为栈顶暂定最优解；将栈中元素依次出栈，并通过公式(10)-公式(13)计算出栈元素与已出栈元素的欧氏距离矩阵S：

(10)

(11)

(12)

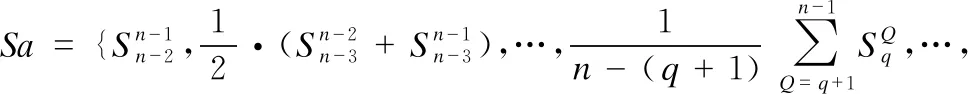
(13)

即可判断应将哪些解纳入用于搜索中心计算的聚集组.计算流程如下：

输入：Solution；

输出：Track；

Step 1.利用公式(10)-公式(13)通过输入的Solution计算得到Sa序列；

Step 2.将Track暂时赋值为栈顶解向量；令k=1；

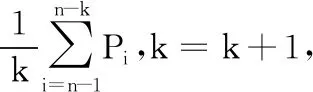
Step 4.当k+2≠n-1时，重复Step 3；否则转Step 5；

Step 5.输出Track；

该子算法在子迭代前期发挥作用，搜索域逐渐收缩之后，由于此时的偏移调整量极小，几乎可以忽略不计，故算法逐渐自动退化，等效于取栈顶解，避免了大幅调整造成的发散解.

3.5 搜索域密度缩放与振荡模块

搜索域密度缩放主要针对子迭代的解空间，而振荡模块主要对主迭代解空间范围更新.3.4中找出更适合作为缩放搜索中心的解向量Track后，若经过载波控制器检测尚未达到精度，则需要重新确定以Track为中心的搜索区域.划定新区域时，需保证新区域不跃出初始搜索域造成解发散，并随搜索域收缩控制混沌轨道长度以减少低效计算量.

设算法当前主迭代解优化次数为epoch；Oup、Odown分别表示初始的up与down序列，Scope=Oup-Odown表示MLC算法初始时设定的搜索域中各个变量的取值尺度；store为最低保留轨道长度；设置搜索域收缩速度为Speed.则对搜索域进行变换后的搜索上下界计算公式如公式(14)、公式(15)所示，其中index表示第index个变量.

newup=Track[index]+Scope[index]·Speed(1+epoch)

(14)

newdown=Track[index]-Scope[index]·Speed(1+epoch)

(15)

搜索域与密度更新的算法如下：

输入：Track；epoch；up；down；times；Scope；Oup；Odown；store；

Step 1.按照变量顺序读取下一个变量搜索域取值；

Step 2.若对于当前变量取值范围[up，down]，根据公式(14)-公式(15)计算newup、newdown.

Step 3.若[newup，newdown]没有超出原始搜索范围Scope=[Oup，Odown]，则取之作为新搜索域边界；否则，将超出的一边的初始边界作为下次迭代的边界；

Step 4.若所有变量的新边界都已计算完毕，转到Step 5；否则，转回Step 1；

Step 5.计算新的轨道长度times=「timesspeed+store⎤；

Speed、store参数根据不同问题可以手动调整.此处为研究方便起见取Speed=0.5，store=500.该算法使搜索域收缩的同时，混沌解规模也随之缩减为原来的一半以节省算力和时间，且由性质4可知混沌系统的特性不会在搜索域收缩后发生改变.

对主迭代中初始搜索域设置振荡缩放过程，防止搜索域收缩过快使全局最优在被发现前被排除，具体如下：

Step1.当发现更优解时，按照公式(14)、公式(15)更新每次子迭代初始的搜索域，转Step 3；否则，转Step 2；

Step2.产生一个随机数，当随机数落在指定收缩概率区间时，按照公式(14)、公式(15)更新每次子迭代初始的搜索域；当随机数落入指定扩张概率区间时，则将公式(14)、公式(15)中Speed的指数改为log2(1+epoch)后按新式子更新每次子迭代初始的搜索域使搜索域回弹.转Step 3；当随机数落入两区间之外，则直接转Step 3；

Step3. 将超出边界的上下限移动到初始边界，主迭代结束，进入停机判断.

如此模拟出低频的搜索域振荡效果，增加全局最优解的发现可能，同时也保持搜索空间的对数型持续收缩.

3.6 载波控制器

载波控制器主要任务为监测每次子迭代构建的解堆栈求得的解值是否达到精度要求并控制重载波.故在每次子迭代末期，停机控制器需要对本次求解得到的解和解值做好记录，以备下次监测使用.评估办法基于解值的差分：

ΔF*=F[(Trackk)-F(Trackk-1)]2

(16)

当检测到ΔF*小于或等于要求的精度值(一般取10-w，w为正整数)，则终止载波和子迭代过程，根据解的优化情况更新搜索域后，进入停机控制器；否则，运行搜索域密度收缩子算法，并向混沌扰动模块输入重载波参数，给予微小扰动后开始新的子迭代.

3.7 停机控制器与混沌扰动模块

停机控制器用于在达到最大迭代次数时终止算法.由于混沌优化算法每次迭代结果都具有随机性，没有有效的解监测办法，故只能用最大迭代次数作为控制因素.

混沌扰动模块通过在混沌系统控制参量上施加10-4的扰动实现对混沌轨道的扰动，即加减一个10-4级的随机数即可.

4 实验分析

4.1 求解性能对比测试

为了验明3中设计的MLC算法是否具有更好的全局最优求解能力，使用了单目标优化常用的测试函数SCHAFFER函数式(17)和“大海捞针”函数式(18)进行算法测试.两个函数在定义域内的图像如图5所示，两个函数都具有被局部最优解包围全局最优解、且全局最优解值与局部最优解值差异较小的特点.

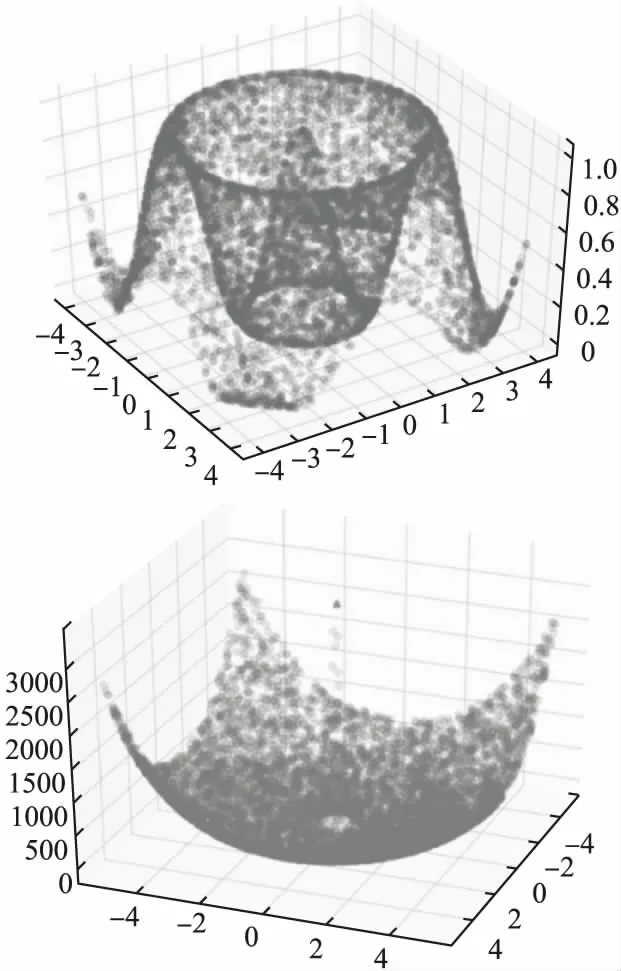
图5 SCHAFFER函数(上)和“大海捞针”函数(下)

(17)

(18)

其中，SCHAFFER函数全局最优解为(0，0)，对应函数值为1，圆环上的局部最优为0.9903，外部的4个局部最优解为0.6468.

实验表明使用Lingo软件求解SCHAFFER所得解值为0.6468488，而使用Matlab可解出解值为0.9903；使用原Logistic混沌优化算法需经过1092次迭代才能得到全局最优解[18]，而使用混沌遗传算法则需迭代458次.“大海捞针”函数全局最优解为(0，0)，对应最优解值为3600，4个角上分别存在4个局部最优解，对应解值都为2748.78；Lingo和Matlab运算出现局部最优概率高达95%，遗传算法也需迭代300代才有60%可能找到最优解.

设置MLC算法初始参数：目标下降精度0.0001，收缩速度0.5，产生混沌轨道长定义为500，最大迭代次数为50次；设振荡收缩概率区间为[0.075，0.01]，扩张概率区间为[0，0.075].分别对两个待优化函数运行10次MLC算法.结果对于两个问题的求解都在3次迭代以内找出都找到了全局最优解，且二者分别进行的10次实验中都有9次都收敛到全局最优解，可粗略认为有接近90%的概率一次计算得到全局最优.

4.2 中等复杂问题求解能力综合测试

为进一步测试MLC算法是否有能力对中等复杂单目标函数进行最优化求解，选择了Ackley函数和Griewank函数作为测试用例，两个函数基本式如公式(19)、公式(20)所示.其中，Ackley函数二维形态如图6所示；Griewank二维形态从[-1000，1000]到[-5，5]区间缩放效果如图7所示，可知Ackley具有顶峰局部最优特性；而Griewank函数同时具有微搜索域褶皱丰富、局部最优与全局最优解值差异极端微弱的特性，搜索域较大时，只能大致判别出最优解在0点附近，但当搜索域缩减后，函数图像上出现大量褶皱，且波峰波谷差距极其微小.这类特性使得二维情况的求解都已经非常困难.分别构造10维Ackley函数和10维Griewank函数，设公式(19)中的d为10，a为20，b为0.2，设公式(20)中的d为10；分别设定Ackley函数变量取值范围为[-50，50]，Griewank函数取值范围为[-1000，1000].此处10维Ackley函数的解空间规模为10010；而10维Griewank函数的解空间规模为200010.已知两函数最优解都为[0，0，0，0，0，0，0，0，0，0]，对应解值0.

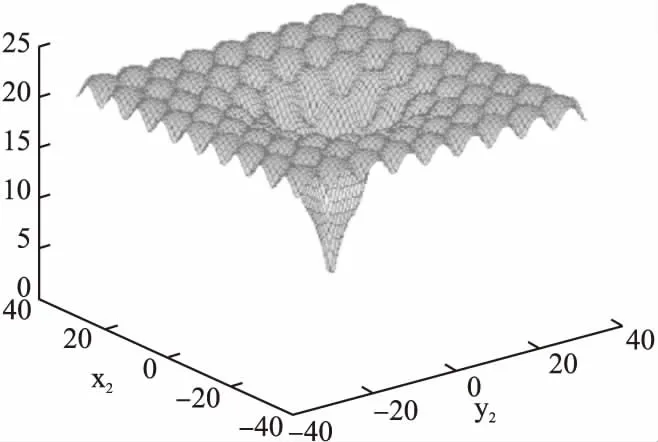
图6 2D Ackley函数

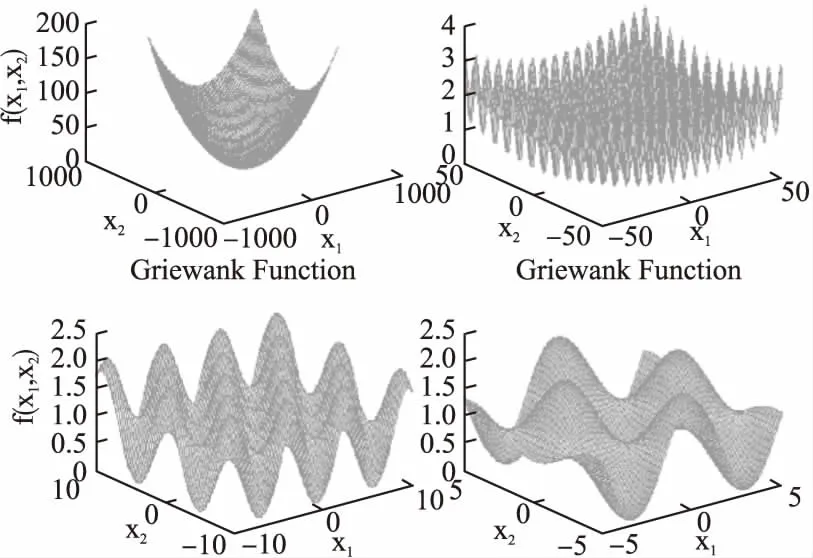
图7 2D Griewank函数

+a+exp(1)，xi∈[-50，50]

(19)

(20)

使用原Logistic混沌优化算法迭代1000次，实验10次，其中有2次分别在632次迭代和944次迭代求得Ackley函数全局最优解；但始终没有找出Griwank函数全局最优解.使用遗传算法、蚂蚁算法测试，都始终无法求出10维Griwank函数的全局最优解.

调整MLC算法参数，设置最大迭代500次，混沌轨道长度为5000，其余参数不变，分别对两个函数运行算法15次.

对于Ackley函数，15次实验都在第1次迭代中就找到全局最优解.对于Griewank函数，15次测试的结果如表3所示，除了6号实验外，其余所有实验都在300次迭代内找到全局最优解，且解值精度达到99.9999%.其中有7次都在100次迭代内找出全局最优解.两轮测试都能够在较500次迭代内有效找到全局最优解，证明MLC算法对于中等连续复杂单目标函数据具有较好的极值求解能力.

表3 10维Griewank函数±1000范围内最小化求解结果

5 总 结

针对常用的遗传算法、蚁群算法一类复杂连续函数求解方法存在的难以跳出局部最优、收敛时间过长等问题，以及基于Logistic混沌系统设计的优化算法存在的边缘过度搜索缺陷，改进Lorenz混沌映射系统设计了一套新的混沌映射系统模型，并基于该模型设计了分片Lorenz混沌堆栈聚集变密度振荡搜索算法(简称MLC算法).通过系统仿真分布统计实验和多轮求解能力测试，达成了以下目标：

1)验证了改进后的混沌模型具有优于Logistic系列混沌的分布均匀度与随机性，更适合作为改进混沌优化算法的搜索轨道发生核心；

2)相对经典优化算法，新算法在解决单目标复杂连续函数极值问题方面具备速度快、性能稳定、局部跳出能力强等优势，能够以较高且稳定的概率直接找出简单函数全局最优解，综合性能优于对比组的各项经典算法和现有软件.

利用MLC算法的优势，可以考虑其应用于工程优化领域，例如计算化工领域复杂化学反应有效产出最大化或废料最小化的原料配置问题；或者用于解决非线性复杂管理科学工程问题，例如对复杂博弈投资组合问题计算投资产出最优方案等；在生物运动信号处理方面，对该算法进行改进还可以用于九轴运动传感器校准.

由于MLC算法框架针对复杂连续函数优化的特异性，该算法尚不可直接用于解决组合优化问题.此外，算法的收敛策略缺乏非线性过程，这使得算法搜索不均衡；解空间的收缩则使算法放弃了边界外的区域.上述不足之处有待后续研究.