蔡金兵

(江苏省启东市汇龙中学 226300)

函数是我们高中数学学习中的一个非常重要的概念，它贯穿在高中数学的各个章节内容中，一直是高考和各地模拟考试重点考查的内容，构造函数并不是一眼就能看出来的，要配合敏锐的洞察力，借助于数形结合，深层挖掘其内在联系.我们在解题过程中，要善于挖掘题目中的隐含条件，构造出我们熟悉的函数,然后巧用函数的某些性质，这是我们构造函数的关键.

一、在不等式中的应用

例1设函数f(x)=x2-aln(x+1)，其中a∈R.

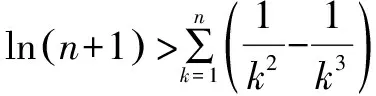
证明当a=1时，则f(x)=x2-ln(x+1).

令h(x)=x3-f(x)=x3-x2+ln(x+1),

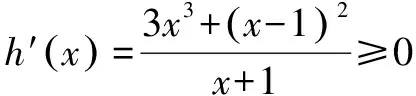
所以h(x)在[0,+∞)单调递增,h(x)≥h(0)=0.

所以ln(x+1)≥x2-x3.

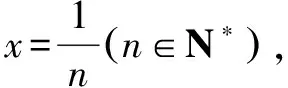
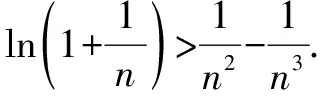
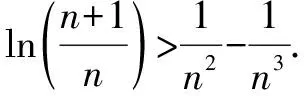
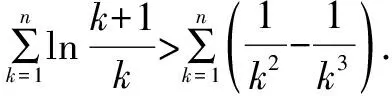
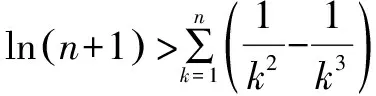
二、在三角函数中的应用

例2函数f(x)=sinx，若f(x)+1≥ax+cosx在[0,π]上恒成立，求实数a的取值范围.

解析不等式等价于ax+cosx-sinx-1≤0.

令g(x)=ax+cosx-sinx-1,

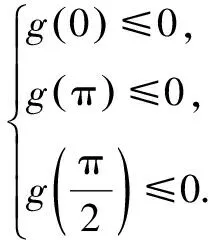
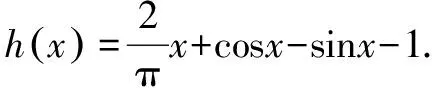
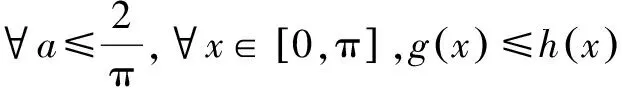
所以若要g(x)≤0，只需h(x)≤0，下面进行证明：

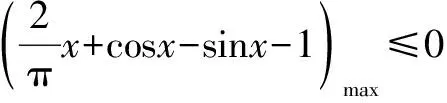
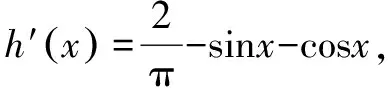
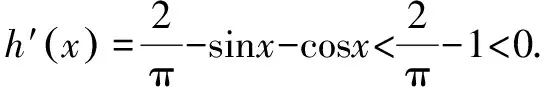
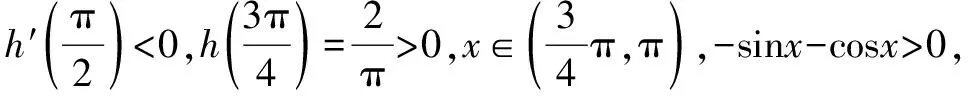
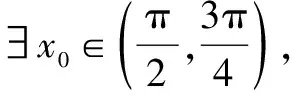
故h(x)在(0,x0)单调递减，在(x0,π)单调递增.

所以h(x)max=h(0)=h(π)=0.

所以h(x)≤0恒成立.

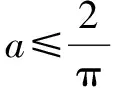
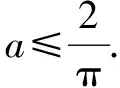
三、在零点问题中应用

例3 已知函数f(x)=|xex|，方程f2(x)+tf(x)+1=0(t∈R)有四个零点，则t的取值范围为____.

解析令g(x)=xex，故g′(x)=ex(x+1).

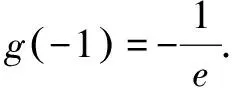
即可绘制函数f(x)的图象如图1所示.

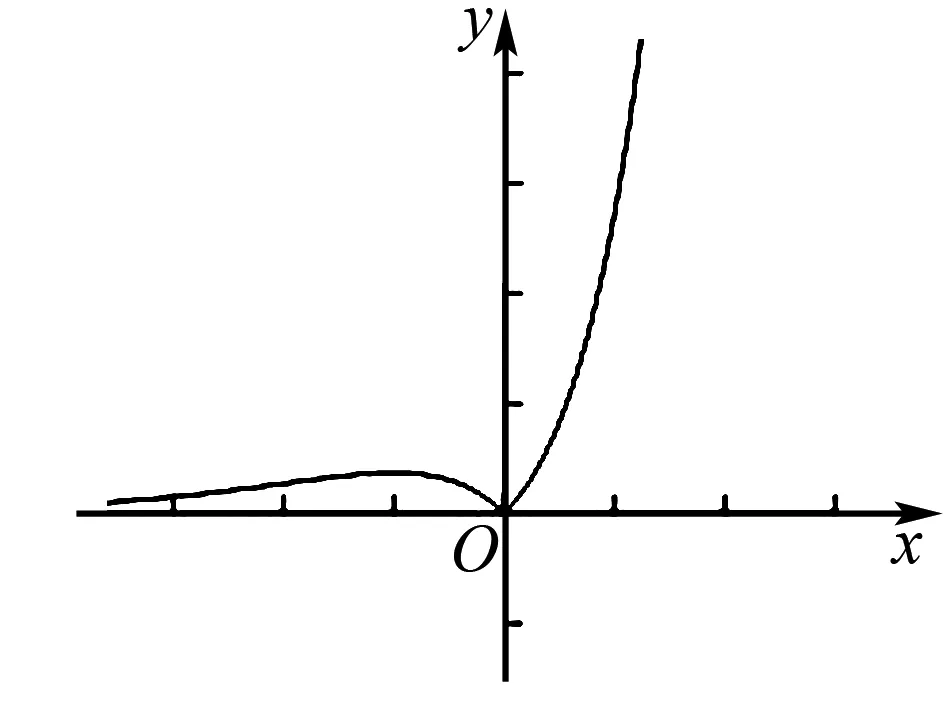
图1

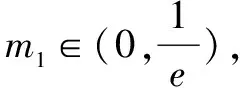
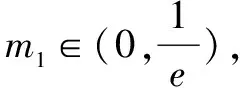
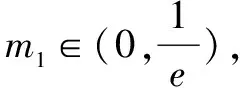
四、在导数中的应用

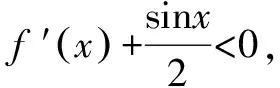
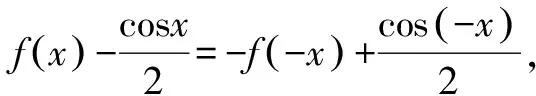
函数思想的本质是指应用我们所熟悉的函数的概念和性质去分析问题、转化问题进而解决困难问题的思想.构造函数思想概括起来有以下几步：

(1)仔细读题，观察题目类型和结构，与我们熟悉的函数有何内在联系，进而构造出可以解决问题的函数；

(2)利用相关函数的性质，配合数形结合等方法，进而得出相应的结论；

(3)可以尝试将不常见的函数模型中的结论返回原理中，进而得出正确的结论，因此构造函数思想在整个高中数学阶段有非常广泛的应用.运用这种方法解题时要抽丝剥茧，配合数形结合，也要注意到恒等变形和不等证明的一些技巧，多方面着手去思考，才能拨开云雾见青天，进而得出问题精巧的解法.