夹层结构屈曲模型的拓展及失效判据
2021-08-03曹鹏宇牛康民
曹鹏宇,牛康民
北京科技大学 材料科学与工程学院,北京 100083
自20世纪40年代以来,夹层结构就被广泛地应用于制造轻质结构,是航空航天、航海等重要工业领域中的一种常用结构材料。尤其是在航空工业中,因其抗失稳能力强,又能够减轻飞机的重量,所以得到了广泛的应用。屈曲[1]是夹层结构最主要的失效模式之一。
由于夹层结构在工程上的重要性,为指导其结构设计,自20世纪40年代开始,国际上进行了大量关于夹层结构屈曲的理论研究,Allen[2]总结了早期夹层板屈曲的经典理论。
中国自20世纪80年代起也开展了大量关于夹层结构的理论及实验研究,如丁运亮和刘毅[3]利用有限元技术对复合材料夹层结构前机身进行结构优化设计。胡培[4]研究了飞机夹层结构的芯层选择方案和设计方法。在夹层结构中,比较常用的面板材料有铝板、纤维增强复合材料等,比较常用的芯层材料有泡沫芯层、蜂窝芯层。基于此,汤超等[5]和王华吉[6]分别研究了泡沫夹层结构复合材料和蜂窝夹层结构复合材料的力学性能。在王兴业[7]的著作中,详细讨论了夹层结构的基本原理、稳定性以及如何进行工程设计等。李汪颖等[8]针对夹层结构声学设计问题开展了声辐射特性拓扑优化研究。周华志和王志瑾[9]建立了带有缺陷的皱褶芯材有限元模型并研究了几何参数对M-型皱褶芯材能量吸收率的影响。陈晓和周贤宾[10]完成了夹层板精密成型数值模拟。许泽等[11]求解了弯扭载荷下夹层板的屈曲问题。
早期的学者们提出了很多经典理论模型[2,12],这些模型具有较大的分散性,针对不同类型的夹层板以及失效模式往往需要使用不同的模型。除此之外,由于在推导过程中引入了较多的假设,导致这些模型的精度较低,但是其形式上的简洁便于工程师的使用。
此后的研究者尝试建立更高精度的模型并寻找不同屈曲模式之间的联系,进而建立一种形式上统一的模型。如Léotoing等[13]利用高阶梁理论提出了一种同时适用于整体屈曲和3种局部屈曲模式的新模型。Cao和Niu[14]论证了采用高阶梁理论对芯层建模会使得局部屈曲应力的模拟结果存在一定偏差。Niu和Talreja[15-16]利用应力函数法分别建立了适用于局部屈曲和整体屈曲的精确统一理论模型。Jasion等[17]完成了夹层梁和夹层圆板整体屈曲和局部屈曲的理论、数值及试验研究。后来,Douville和Le Grognec[18]利用拉格朗日方程提出了一种新的模型,经证明他们的结果与Niu[16]得到的结果是一样的。
文献[14-18]在解决夹层结构的屈曲问题中采用了更精确的建模方法,提升了模型的精度并找到了各个屈曲模式间的联系,但是尚未考虑面板在屈曲过程中的横向剪切变形。笔者认为在局部屈曲模式下,更合理的建模方式是将面板视为由许多长度为l0的“短梁”组成,由于屈曲波长变得更短,根据Timoshenko梁理论[19],这些“短梁”的横向剪切效应就不能够随意忽略。此外,由于复合材料层合板在夹层板面板上的应用,因复合材料层合板相对于各向同性材料的剪切刚度更弱,横向剪切对其造成的影响更大,面板的横向剪切效应更应该受到重视。
本文首先基于弹性理论建立一个新的精确屈曲模型,并在建模过程中引入面板的横向剪切效应;然后,为建立高精度且形式简单的屈曲公式,根据不同的屈曲模式化简理论解,得到高精度且形式简单的屈曲应力表达式;最后,对比屈曲公式解与数值解,以期验证建立的屈曲失效准则的精度。
1 经典理论回顾


图1 整体屈曲及3种局部屈曲模式
在早期的经典模型中,Allen[2]首先给出了各向同性芯层夹层板3种局部屈曲模式下具有统一形式的临界载荷表达式:
(1)
式中:σf为面板中的轴向压应力;上标f和c分别代表面板和芯层;B为参数,其值取决于模量比Ef/Ec和厚度比tc/tf;E和t分别为各层的拉伸模量和厚度。Plantema[12]改进了 Allen[2]的公式并在模型中引入了芯层的剪切模量:
(2)
式中:C为参数;G为剪切模量。式(2)可以应用于具有正交各向异性芯层的夹层板(如蜂窝芯层)。Simitses和Hutchinson[20]采用经典的弹性地基梁假设,得出关于式(2)在单边屈曲模式下的不同形式:
(3)
式中:k为芯层作为弹性地基的弹簧刚度,k=Ec/tc;D为面板的弯曲刚度,对于梁结构,D=EfI,其中I为梁截面关于中性轴的惯性矩。单边屈曲模式可以认为是对称屈曲模式的一半,因此式(3)也可以用来预测对称屈曲模式的临界应力。
Allen[2]同时也建立了一种基于反对称平面芯层假设的模型,确定了反对称屈曲模式下的临界应力:
(4)
如果厚度比tc/tf≫1,式(4)可简化为
(5)
式(5)代表了一类称为“剪切卷边”的屈曲模式,指的是具有中等屈曲波长的屈曲模式。这类屈曲通常是由芯层的不稳定性引起的,Davies[21]认为式(5)适用于跨度较短的夹层板。
屈曲波长定义为屈曲正弦波的一半,Allen[2]给出了半无限厚芯层夹层板的屈曲波长:
(6)
式中:νc为芯层的泊松比。对于单边屈曲,Simitses和Hutchinson[20]采用弹性地基梁假设给出屈曲波长为
(7)
式(1)~式(7)为适用于夹层板屈曲的一些经典模型,这些模型的特点是分散性较大,精度和适用范围有待评估,但是形式简单,适合于工程应用。在工程设计中,针对不同的屈曲现象,设计者不得不采用不同的模型,即使对于同一个理论模型,不同的研究者对方程中的参数也取了不同的值。例如,对于式(1)中的参数B,由于模型的过度简化,研究者们不得不采用经验系数B对模型进行修正。在第3节的分析中,会证实精确理论解在不同的条件下等同于经典公式式(1)~式(5)。
2 理论解
2.1 基本假设
夹层结构的面板被理想化为梁或板支撑在弹性的芯层介质上;认为芯层是一个二维的连续弹性体,利用弹性理论,不引入关于芯层的任何假设。夹层板的面板被理想化为弹性梁结构或板结构,并利用Timoshenko梁理论建模,进而引入面板的横向剪切效应。芯层被假设处于平面应力状态下,在平面应力假设下获得结果可以转化为平面应变状态的结果[19]。
2.2 弹性解析解
采用图1中的坐标系,利用应力函数法选取合适的应力函数描述芯层中场的变化,应力函数φ(x,z)必须满足相容方程[19]:
(8)
选取φ(x,z)满足艾里应力函数的形式:
φ(x,z)=
(9)
式中:
(10)

假设夹层板在x方向是无限长的,其中一个面板的轴线纵向位移函数可以假设为余弦形式:
(11)
式中:An为振幅;n为波数;αn=tf/l0。对于另一个面板,取:
(12)
式中:η为振幅因子,用于定义上、下面板的振幅比。因为两个面板是可交换位置的,所以可假设-1≤η≤1。参照图1,η=0对应单边屈曲情况;η=1和η=-1分别对应对称和反对称屈曲情况。
在芯层/面板界面处的位移边界条件为
(13)

(14)
式中:κ为Timoshenko梁理论中的剪切修正系数;Qf为梁截面上的合剪应力;A为梁的截面积;Gf为梁的剪切模量。由于界面上应力的连续性,面板的一边是无应力的,而另一边与芯层/面板界面的剪应力相同;又由于面板厚度较薄,可以假设截面上的剪应力呈线性分布。因此,上、下面板的剪切应变分别为
(15)
(16)

图2 夹层板轴向应力平衡
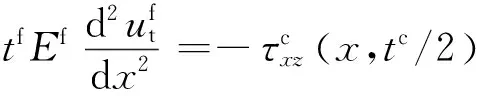
(17)
(18)
由式(17)和式(18)可知,界面上剪应力是引起面板轴线方向位移的主要因素。利用式(11)~式(13)、式(17)和式(18),可以确定艾里应力函数中的常数ci1~ci4和di1~di4。
基于Timoshenko梁理论,面板的总势能为

(19)
式中:φf为梁截面的转角;Df为面板的弯曲刚度;Pf为作用在面板上的轴向压缩载荷;mf为作用在面板上的分布弯矩;qf为作用在面板上的分布正应力。利用最小势能原理,δΠf=0,可得
(20)
(21)
对式(20)求一次导数并代入式(21)中,可得关于φf的微分方程:
(22)
对式(21)关于x求二阶导数,并将式(22)代入其中,可得关于wf的微分方程:
(23)
由于力在界面上的连续性,面板/芯层界面上的分布载荷由式(24)和式(25)定义:
(24)
(25)
最终,可以解得面板中的临界压应力σf为
(1-η)(-Y1+Y2)/X2
(26)
式中:
(27)
根据式(26)可以看出临界应力与定义屈曲模式的因子η呈线性关系。因此,单边屈曲(η=0)的临界应力是对称屈曲(η=1)和反对称屈曲(η=-1)的临界应力平均值。如果将对称模式与反对称模式的临界应力相减,并利用条件K>1及cosh(αntc)>sinh(αntc),可以得到
Ks(2+s2){48+s[8+s(1-νc)]+
12(1-νc)}+2K2s2(12-s2)(3-νc)×
(1+νc)+Ts{2+s[s+K(2-s)(1+νc)]}×
{12+s{8s+s3+2K[3(2-s)+s2]×
(1+νc)}}}/{[(2+s2)cosh(Ts)+
Ks(3-νc)(1-νc)sinh(Ts)]2-[2+
s2+KTs2(1+νc)2]2}
(28)
式中:σII和σIII分别为对称屈曲和反对称屈曲的临界应力。
式(28)在条件式(29)成立时总是成立的:
(29)
式(29)在梁理论的假设下总能成立,因此可以得出结论:反对称屈曲模式的临界应力总是低于对称屈曲模式的临界应力。
式(26)可以化简为以夹层板厚度比tc/tf、模量比Ef/Ec为参数、面板与屈曲波长比值tf/l0为自变量或芯层与屈曲波长比值tc/l0为自变量的函数。图3和图4分别给出了以tf/l0和tc/l0为自变量的由式(26)所得精确解的应力曲线。

图4 横坐标为tc/l0时不同参数下式(26)所得精确解的应力曲线
首先,从图3中可以看出,反对称模式的临界应力总是低于对称模式的临界应力,这与式(28)的分析吻合。随着屈曲波长的减小,反对称模式和对称模式的临界应力变得几乎完全相等。当厚度比增加至某一临界值时,应力曲线在短波区域形成了一个极值,这一极值对应着局部屈曲应力;此时,局部屈曲的应力值有可能低于整体屈曲应力(取决于夹层板的长度),进而变为首先出现的失效模式。除此之外,可以看到对称模式与反对称模式的局部屈曲应力是相等的,这意味着当夹层板的厚度增大至某一临界厚度后,上、下面板的屈曲将不再相互干涉。又由于式(26)关于η是线性的,3种局部模式的局部屈曲应力实际上是相等的。
以不同的自变量描述临界屈曲应力函数具有不同的物理意义。例如,在图3中,以tf/l0为自变量时,可以看到在短屈曲波长范围内,夹层板的局部屈曲应力及对应的面板厚度与波长之比tf/l0只受夹层板的模量比Ef/Ec影响。根据引言中提到的“短梁”假设,tf/l0即代表了“短梁”的细长比;根据Timoshenko梁理论,tf/l0衡量面板的横向剪切效应。因此,面板的横向剪切效应大小只受夹层板模量比的影响。综合对比图3可以得出结论,tf/l0是随着夹层板的模量比Ef/Ec的减小而增大的,也即模量比Ef/Ec越小,局部屈曲应力受面板横向剪切效应的影响越大。
当以tc/l0为自变量时(图4),可以看到随着厚度比增大到某一临界值后,局部屈曲应力不再发生改变;这代表当芯层厚度大于屈曲波长达到某一临界值后,上、下表面的屈曲将不再相互干涉,此时芯层相当于无限厚;tc/l0可用来衡量芯层的这一临界厚度,当芯层超过这一厚度时,上、下表面的相互作用几乎为0,故局部屈曲应力不受厚度比变化的影响。从图4可以看出,这一临界tc/l0约为1.5。
需要指出的是,参数范围选择是具有普适性的。在模量比Ef/Ec的变化范围为10~1 000的情况下选取了较宽范围的厚度比,并涵盖了临界厚度比。
3 理论解的近似公式
注意到在式(11)中波数n的取值范围为1~∞。当屈曲波数n=1时,意味着屈曲波长l0等于夹层板的长度L,对应整体屈曲模式。当n较大时,对应周期性的局部屈曲模式。通过界定屈曲波长范围建立式(26)所得精确解在全屈曲波长范围内的近似公式(式(32)、式(44)及式(46)),并讨论了一些经典解的适用性。随后,根据近似公式式(32)、式(44)及式(46)建立了夹层结构受压缩载荷和弯曲载荷的屈曲失效准则。
3.1 长屈曲波长范围
在长屈曲波长情况下,如果芯层和屈曲波长的比值很小:
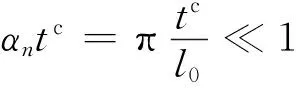
(30)
利用等价关系cosh(αntc)≈1+(αntc)2/2和sinh(αntc)≈αntc+(αntc)3/6,式(26)可以化简为
6Ktctf+4(tf)2(2-3Kνc)]}}/
(31)
近似表达式式(31)仍然以η的值定义3种屈曲模式。当夹层板受轴向压缩载荷时,根据式(31),利用函数求极值的方法可获得反对称屈曲模式下(η=1)的临界应力为
(32)
此时的屈曲波长为
(33)
进一步,如果L2≫π(tc)2、4K≫tc/tf,式(32)可以化简为

(34)
式(34)与Allen[2]建立的基于反平面芯层假设、面板较厚的夹层板屈曲公式相同。这说明相比于精确解析解,Allen的模型[2]只适用于一些特殊的夹层板,如当面板的厚度较薄时及面板与芯层模量比K较小时,式(32)和式(34)是不能近似相等的。对于跨度L较短的夹层板,式(34)等号右侧第1项可近似为经典公式式(5)。这说明对于长度较短的夹层板,式(5)可以作为整体屈曲应力的设计准则。但在大多数情况下,采用式(32)能得到更精确的结果。
当η=0时,可以求得单边屈曲模式在长屈曲波长范围内的近似公式。然而,直接利用函数求极值的方法计算式(31)存在一定困难,所以额外引入了假设Ktf/tc≫1,式(31)化简为
(35)
利用式(35)及函数求极值的方法,可得单边屈曲的临界应力值为
(36)
对应的屈曲波长为

(37)
如芯层的泊松比为0,式(36)等号右侧第1项与Simitses和Hutchinson[20]得到的式(3)是一样的,屈曲波长式(37)和式(7)是一样的。实际上,由于在数学推导过程中引入了额外的假设,式(36)并不能对单边屈曲的临界应力给出很好的预测结果。例如,当厚度比tc/tf较大时,式(36)等号右侧第1项趋于0,但是另外两项会变得很大。此时由式(36)计算的临界应力会变得过分保守,因此它提供的并不是一个可靠的结果。进一步详细讨论如何合理地利用式(36)建立夹层板承受弯曲载荷下的近似公式。
3.2 短屈曲波长范围
在短屈曲波长情况下,如芯层和屈曲波长的比值很大,即

(38)
那么此时可以得到
(39)
利用条件式(39),式(26)针对所有屈曲模式可以化简为统一形式的表达式:
s(1-νc)]+12(1-νc)}}}}/{2Ks(6+s2)×
{2+s[s+K(3-νc)(1+νc)]}}+
(40)
如果忽略面板的剪切效应,即tf/l0≪1,式(40)可以化简为
(41)
进一步,如果假设Kαntf≫1,式(41)可化简为
(42)
数值结果显示,式(42)中括号内的第3项对临界应力σf的贡献很小。因此忽略第3项并对式(42)求极值,得局部屈曲的近似波长为
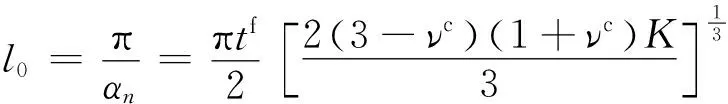
(43)
式(43)与假设芯层是半无限大的式(6)得到的屈曲波长是一样的。将式(43)代入式(42)可得局部屈曲临界应力的近似公式:
(44)
式(44)的特点在于应力只取决于夹层板的材料参数,而不涉及夹层板的几何参数。式(44)等号右侧第1项与Allen[2]和Zenkert[22]得到基于弹性地基梁模型、只考虑芯层对面板正应力的局部屈曲应力表达式是相同的。这证明式(44)等号右侧第1项是由芯层对面板的正应力引起的,其余两项则是由芯层/面板界面上的剪应力引起的。Allen[2]曾指出,如果面板的厚度很薄,由界面剪应力引起的弯矩对屈曲载荷造成的影响是可以忽略的。但根据式(44),局部屈曲应力是不受面板厚度影响的。实际上,通过计算可以发现当面板与芯层的模量比K较小时,忽略后两项所引起的误差会很大。例如,经计算当K=10、νc=0.3时,这一误差达到了约15%。式(44)是在tf/l0≪1条件成立的前提下得到的,注意到因模量比Ef/Ec较低时,tf/l0会逐渐变大,因此式(44)与精确解析解(26)之间的误差会有微小的增加,但是由图3 可知,这一误差仍在可接受范围之内,在工程上利用式(44)预测临界应力仍然可以给出可靠的结果。
3.3 屈曲失效判定准则
在3.1节和3.2节中,以波长为界定范围,从数学角度建立了精确解在不同波长范围内的近似公式。根据3.1节和3.2节的近似公式,建立了夹层结构在两种典型载荷(轴向压缩及弯曲)下的屈曲失效判定准则。
首先,图5给出了式(26)的弹性解析解与式(32)的长波近似公式解的对比。可以看到在长屈曲波长范围内(tc/l0≪1),式(32)的长波近似公式解都与式(26)的弹性解析解吻合得很好,因此可以用式(32)预测长波屈曲的临界应力。当厚度比tc/tf较大时,应力曲线在短波区域内形成了一个新的峰值,这个峰值对应着局部屈曲应力,根据3.2节中的分析,利用近似公式式(44)可以更好地预测这一临界应力。

图5 长波近似解与精确解对比
要建立精确的屈曲准则不仅需要考虑长波屈曲和短波屈曲范围内的临界应力,还需要考虑处于过渡范围内的临界应力(也即中等波长范围,tc/l0的数量级约为1左右)。实际上,由图4可以看出,在中等波长的范围内,式(44)仍然对临界应力给出了较为准确的预测,直到长波近似公式式(32)给出的临界应力更低。因此,在工程上当夹层板受轴向压缩载荷时,提出设计准则:
(45)
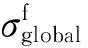
当夹层板受弯曲载荷时,对应单边屈曲失效模式(η=0)。根据2.2节中的分析,在短屈曲波长范围内,单边屈曲的局部屈曲应力等同于对称屈曲模式和反对称屈曲模式的局部屈曲应力。但是存在一些较为特殊情况,当夹层板的厚度比变得非常小时,夹层板的屈曲应力对应于长波屈曲范围(见图6),此时弯曲临界应力和式(44)预测结果误差较大。
在3.1节的分析中提到,当η=0时,单边屈曲近似公式式(36)后两项产生的结果不适用于预测长波范围内的屈曲应力。但是如果只取式(36)等号右侧第1项(与用于预测单边屈曲的经典模型式(5)近似),即
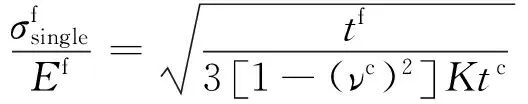
(46)
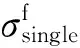

图6 单边屈曲模态精确解与近似解对比
(47)
式中:下标b表示夹层板受弯曲载荷。
3.4 数值验证
为验证屈曲失效准则的准确性,利用有限元商业软件ABAQUS[23]计算了几个数值实例的屈曲特征值,并与理论结果作对比。
依据表1和表2中给出的几何和材料参数建立二维的数值模型。芯层和面板都是由8节点、双二次平面应力单元组成的。面板和芯层间的节点是刚性连接的,通过施加适当的边界条件,经计算可得到屈曲特征值。
由表1和表2的结果可以看到,建立的解析公式解与数值结果吻合得非常好,最大误差不超过2%。

表1 轴向压缩下式(32)、式(44)与数值解的第1阶屈曲模式及特征值对比

表2 弯曲载荷下式(44)、式(46)与数值解的第1阶屈曲模式及特征值对比
4 结 论
1)建立了一种新的引入面板横向剪切效应的、适用于所有屈曲模式的精确理论模型,并评估了横向剪切效应对夹层板屈曲的影响。
2)建立了适用于不同屈曲模式的、形式简单的屈曲公式,证明了在不同条件下精确理论解等同于经典公式。
3)根据得到的屈曲公式建立了适用于压缩载荷和弯曲载荷下夹层板的屈曲失效判定准则;通过与数值结果作对比,验证屈曲公式保持了足够高的精度,并且屈曲公式形式简洁,非常适合工程应用。
