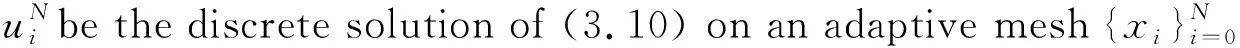Abstract：A nonlinear singularly perturbed Volterra integro-differential equation is studied. This equation is discretized by an upwind finite difference scheme for which a priori error analysis in the maximum norm is derived. Based on the a priori error bound, a first-order rate of convergence, independent of the perturbation parameter, is established by using the priori bounds of exact solution and equidistributing the standard arc-length monitor function.

Key words：singularly perturbed; Volterra integro-differential equation; uniformly convergent; adaptive grid method

1 Introduction

In this paper we consider the following nonlinear singularly perturbed Volterra integro-differential equation

(1.1)

where0<ε≪1,a(x)≥α>0,K(x,s,u)is a sufficiently smooth function,Ais a given constant, andf(x) is a funtion inC1(Ω) that is regular with respect toεasε→0.

Singularly perturbed Volterra integro-differential equations can be found in a widespread array of areas including diffusion-dissipation processes, epidemic dynamics, synchronous control systems, renewal processes, filament stretching problems and many others (see, e.g., [1-6]). In general, when the perturbation parameterε→0, the solution of these problems typically exhibits a boundary layer atx=0. Therefore it is difficult to obtain accurate numerical results for these problems by using standard numerical methods. For this purpose, a lot of researchers paid attention to some special numerical methods for these problems. The implicit Runge-Kutta methods were developed for singularly perturbed Volterra integro-differential-algebraic equations in [7] and for singularly perturbed Volterra integro-differential systems in [8]. Horvat and Rogina[9] presented the spline collocation methods for singularly perturbed Volterra integro-differential equations and Volterra integral equations in certain tension spline space. In [10], the authors proposed an exponentially fitted difference scheme constructed in a uniform mesh for singularly perturbed Volterra integro-differential problems. Extended one-step schemes of exponential type were presented in [11], while exponential techniques and implicit Runge-Kutta methods were introduced in [12] for solving singularly perturbed Volterra integro-differential problems. In [13], Sevgin studied a uniformly convergentε-numerical method on a graded mesh for the Numerical solution of a nonlinear singularly perturbed Volterra integro-differential equation. Recently, Iragi and Munyakazi[14] presented a finite difference method which combines backward Euler difference operator for the differential part and repeated quadrature rules for the integral part to solve a linear singularly perturbed Volterra integro-differential equation. The authors in [15] presented an adaptive algorithm based on a posteriori error analysis to cope with a singularly perturbed Volterra integro-differential equation with an integrable singularity in the integral term.

Motivated by the works of [10,13,15], we will propose an adaptive grid method for (1.1). A finite difference method on an arbitrary nonuniform mesh is applied to discretize the problem (1.1) and an adaptive grid generation algorithm based on the arc-length equidistribution principle is used to capture the singular phenomena. In addition, we not only derive a posterior error estimation, but also give a priori error estimation, which makes our conclusion more convincing.

NotationThroughout this paper,C, sometimes subscripted, is a generic positive constant independent ofεand the mesh parameterN, which can take different values at different places.

2 The continuous problem

In this section, we study the stability results for the exact solution of the problem (1.1), which are required for the analysis in the next section.

First, in order to give the bounds of the exact solutionu(x) of (1.1) and its first derivative, the problem (1.1) can be linearized as

where

Lemma2.1The solution of the problem (1.1) satisfies the following inequalities

‖u‖∞≤C(|A|+a-1‖q‖∞),

(2.1)

(2.2)

ProofThe proof is similar to Lemma 2.1 of [13].

3 Discrete scheme and stability results

3.1 Discrete scheme

(3.1)

where

(3.2)

(3.3)

Using the left rectangular integral formula to approximate the integral of (3.1), we get

(3.4)

with local truncation error

(3.5)

To obtain the approximation of the integral term of (3.3), we use the quadrature formula

(3.6)

with local truncation error

(3.7)

It follows from (3.3), (3.4) and (3.6) that

(3.8)

where

(3.9)

Neglecting the local truncation errorRiin (3.8), we obtain the following discretization scheme for the problem (1.1):

(3.10)

3.2 Stability results

(3.11)

where0<γ<1 and

(3.12)

Next, in order to derive the stability of (3.10), we first give the following lemma. The proof follows the argument given in Lemmas 4.1-4.4 of [13].

Lemma3.1 Assume there exists a constantα*such that

(3.13)

Then

(3.14)

ProofIt follows from (3.12) that

where

Obviously,

By (3.13), it is easy to see that

Then the inequality (3.14) follows from Lemma 4.1 of [13].

Theorem3.2Under the condition (3.13), the solution of the scheme (3.10) satisfies the following stability estimate

(3.15)

(3.16)

Furthermore, we have

(3.17)

It follows from Lemma 3.1 and (3.17) that

(3.18)

Applying the Gronwall inequality (see Lemma 3.2 of [21]) to (3.18), we obtain

(3.19)

which leads to the desired result.

4 A priori error analysis based on mesh equidistribution principle

In this section, in order to derive a priori error estimate for the discrete scheme (3.10) on an adaptive nonuniform mesh, we give the following mesh equidistribution principle.

(4.1)

(4.2)

As far as we know, the standard arc-length monitor function

(4.3)

was widely used in designing the adaptive grid algorithm for singularly perturbed convection-diffusion equations (see [16-20]). In this paper, we also choose (4.3) as the monitor function to design an adaptive grid method for the problem (1.1). Furthermore, combining with (4.2) and (4.3), we have

(4.4)

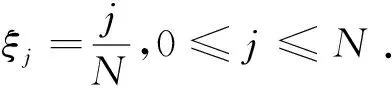
(4.5)

Moreover, we obtain

(4.6)

Based on the estimations (2.1) and (2.2),we can obtain the following lemma:

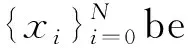
L≤C,

(4.7)

hi≤CN-1,i=1,2,…,N.

(4.8)

ProofThe proof is the same as that of Lemma 3.1 of [20].

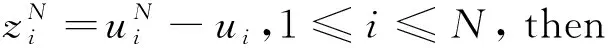
(4.9)

where the truncation errorRiis given by (3.9) andK*is given by

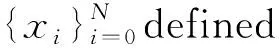
‖R‖∞,ΩN≤CN-1.

(4.10)

ProofIt follows from (3.5) that

(4.11)

Similarly, for the truncation error (3.7), we obtain

(4.12)

(4.13)

Finally, combining withhi≤CN-1, (4.11) and (4.12), we have

‖R‖∞,ΩN≤‖R(1)‖∞,ΩN+‖R(2)‖∞,ΩN≤CN-1,

which completes the proof.

(4.14)

ProofApplying intermediate value theorem for the problem (4.9), we have

(4.15)

where

Then we can prove inequality (4.14) by applying Theorem 3.2 to (4.15). Based on Lemma 4.2 and Lemma 4.3, we obtain the following main result.