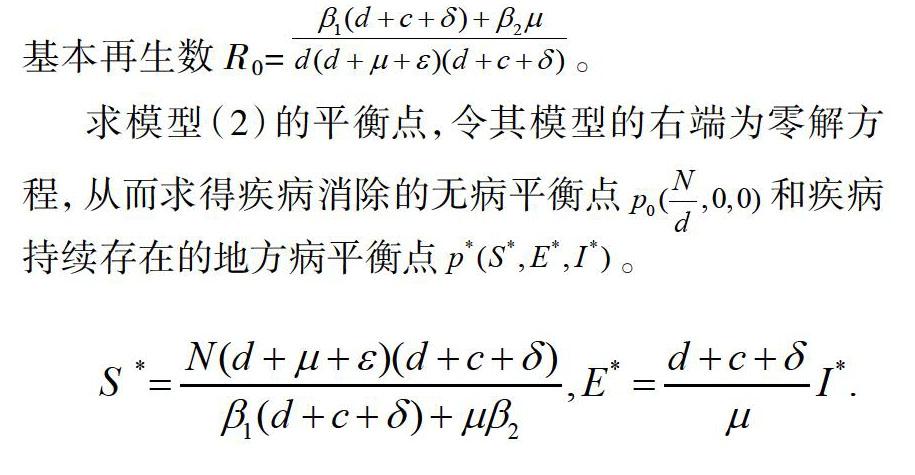
DOI：10.16661/j.cnki.1672-3791.2103-5042-3263

摘  要：该文以一类具有标准发生率且潜伏期具有传染性的SEIR传染病模型为研究对象，首先通过计算得出决定疾病灭绝或持续存在的基本再生数、模型存在的无病平衡点和地方病平衡点，其次运用LaSalle不变集原理和构造适当的Lyapunov函数，证明当r0<1时，无病平衡点的局部和全局渐近稳定，此时流行病将会逐渐趋于灭绝而不会大规模爆发。

关键词：基本再生数  标准发生率  潜伏期  Lyapunov函数  全局渐近稳定

中图分类号：O175.1                          文献标识码：A文章编号：1672-3791（2021）03（b）-0221-03

Stability Analysis of SEIR Model for a Class of Latent Infection

DOU Zhongli

（Chongqing Finance and Economics College， Chongqing， 401320  China）

Abstract： In this paper， we study a class of a standard incidence of SEIR epidemic model of the incubation period is contagious， first of all， calculated decision to extinction or persistent disease basic reproductive number of disease-free equilibrium and the endemic equilibrium model， then using the LaSalle invariant set principle and constructing suitable Lyapunov function， proved that， When ro<1， the local and global asymptotic stability of the disease-free equilibrium and the epidemic will gradually become extinct without large outbreaks.

Key Words： Basic regeneration number; Standard incidence rate; Incubation period; Lyapunov function; Globally asymptotic stability

在现实生活中，传染病的广泛存在对人类的生存和社会的发展构成很大的威胁。例如，苏联在1990年发生白喉流行病，波及东欧15个国家，死亡人数超过10万;早在20世纪80年代初发现的艾滋病，已在全球夺取了2 500万人的性命，死亡人数超过第一次世界大战，现在仍然没有任何药物可以治疗它。但是人类仍然积极在对抗这种免疫系统疾病，没有丧失战胜它的决心。2003年爆发的SARS病毒涉及到32个国家和地区，病死率达到11%;2015年持续蔓延的埃博拉病毒有9万多人死亡，病死率高达50%和2020年初流行的新冠肺炎使全球超过20万人死亡等，流行病时刻在威胁着人类的健康。

人类对于传染病的传染源、传播途径、发病原因、发病机理、传播速度、流行规律的研究从未停止。传染病在传播过程中与人生活的环境有关，传播过程中存在着“环境-人”与“人-人”两种途径。数学家们利用传染病的传播特点结合数学本身的理论知识研究传染病的动力学性态，得到一些关于传染病流行的更专业的理论结果，医生利用这些理论结果解决传染病的传染问题。因此，利用动力学方法建立传染病模型，分析流行病的发病原因、寻求防治策略、预测疾病的流行规律已成为重要的研究内容，是现在备受关注的热点问题之一。

1  模型建立

近几十年来，传染病动力学快速发展，由于传染病传播的不确定性和多样性，关于传染病问题的研究始终无法完美地解决，但是大部分传染病问题都可以用数学模型来分析。关于传染病生物数学模型[1]，已经有很多专家和学者进行研究。例如：传染病有“人-人”现象，专家给出隔离来切断传播途径，并通过接种疫苗来预防传染病的传播。但是有一些传染病具有一定的潜伏期，因此文献[2-4]研究了一类具有潜伏期的传染病模型，这类模型考虑了传染病在染病期間具有传染性，研究了模型的局部和全局稳定性，但是没有考虑在潜伏期间也具有传染性;文献[5-8]研究了传染病在潜伏期和染病期都具有传染性，但是文中采用的双线性发生率。当生存的环境中人数很多时，患病者与人数成正比的接触率和实际的情况不太符合，因为在一定的单位时间内患病者所能接触到易感者的数目是有限的;文献[9]考虑了具有染病者康复的传染病模型，但是文中只是在总人口数量不变的情况下进行讨论，而人口数量是在发生变化的有一定的局限性。通常对于群居的人类和某些种群来说，标准发生率会比双线性发生率更符合实际。因此，该文在上述文献研究的基础上，以一个更接近实际情况且复杂的标准发生率，研究在潜伏期和染病期均具有传染性的传染病模型。

式中，S（t）、E（t）、I（t）、R（t）分别表示t时刻易感者、潜伏者，染病者和恢复者人群数量：N表示总人口量，表示标准传染率：d表示自然死亡率：μ表示潜伏者转化为染病者的转化率：ε、c表示潜伏者和染病者的恢复率：δ表示因病死亡率，参数d、μ、ε、c、δ为非负。由于模型（1）中前3个方程不含R，该文仅关心疾病是否流行，故可以不考虑模型（1）中的第四个方程，仅讨论由前3个方程所构成的传染病模型的动力学性态。由前面3个方程构成的平面系统为：

該文仅在正向不变集内，讨论模型（2）的动力学性态。

2  基本再生数和无病平衡点的稳定性

一个病人在平均患病期内所传染的人数，称为基本再生数[10-11]。基本再生数是用来区分疾病是否流行的阈值，当基本再生数比1小，即染病者在平均患病期间传染的人数比1小，模型在正向不变集D内只存在着无病平衡点是全局渐近稳定的，疾病自然会逐步趋于灭绝;反之若基本再生数比1大，即染病者在平均患病期传染的人数比1大，模型在D内还存在着地方病平衡点是稳定的，疾病将始终存在而逐渐形成一种地方病。该模型利用再生矩阵法计算可以得到模型（2）的基本再生数 R0=。

求模型（2）的平衡点，令其模型的右端为零解方程，从而求得疾病消除的无病平衡点和疾病持续存在的地方病平衡点。

引理：若线性化矩阵的所有特征值均具有负实部，则模型的解是渐进稳定的;若线性化矩阵的所有特征值均具有非正实部，或者其具有零实部的特征值仅有单重初等因子，则模型的解是稳定的;若线性化矩阵至少有一个正实部的特征值，或者有多重初等因子的零实部特征值，则系统的解是不稳定的[11]。

定理1：当时，模型（2）的无病平衡点是局部渐近稳定的[12-13];当时，模型（2）的无病平衡点是不稳定的。

证明：通过线性化得到模型（2）在无病平衡点处的Jacobi矩阵为：

因此得到特征方程为：

显然，该模型有一个特征值λ1=-d<0，另外两个特征值满足方程，其中：

当时，有，，3个特征值的实部均小于零，由引理可知，模型（2）在无病平衡点处是局部渐近稳定的。

当时，有，有一个特征值实部大于零，由引理可知，模型（2）在无病平衡点是不稳定的。

定理2：当时，模型（2）的无病平衡点是全局渐近稳定的。

证明：构造适当的Lyapunov函数为[14]：

沿模型（2）轨线的全导数有：

当R0<1时，由Lasalle不变集原理可知，当时间趋于无穷时，模型的解均有染病者趋于零，易感者趋于N/d，而D中所有轨线均趋于无病平衡点，因此模型（2）的无病平衡点在D内是全局渐近稳定的。

3  结语

该文讨论了具有更接近实际生活的标准发生率的SEIR传染病模型，利用再生矩阵法得到模型的基本再生数，求出模型的无病平衡点和地方病平衡点;利用LaSalle不变集原理和Lyapunov函数，证明当R0<1时，模型的无病平衡点的局部和全局渐近稳定性，这意味着，在生存的环境中无论开始感染的病人有多少，传染病都不会大规模流行而是逐渐趋于灭绝。关于模型的地方病平衡点的局部和全局渐近稳定性有待于进一步解决。

参考文献

[1] 马知恩，周义仓，王稳地，等.传染病动力学的数学建模与研究[M].北京：科学出版社，2004：33.

[2] 豆中丽，王锐.一类具有饱和发生率和潜伏期的SEIR模型的稳定性[J].中山大学学报：自然科学版，2019，58（2）：155-160.

[3] 米晓丽.一类含潜伏期且总人口在变化的SEIRI传染病模型的全局稳定性[J].山西师范大学学报：自然科学版，2015，29（1）：15-18.

[4] 张改平，董玉才，许飞，等.具有垂直传染且总人口在变化的SIRS传染病模型的渐近分析[J].数学的实践与认识，2011，41（18）：139-143.

[5] 梁桂珍，郝林莉.一类潜伏期和染病期均传染的SEIQR流行病模型的稳定性[J].西南师范大学学报：自然科学版，2020，45（3）：1-9.

[6] 杨金根，王铁英，张萍.潜伏期和染病期均传染且具脉冲接种的传染病模型[J].信阳师范学院学报：自然科学版，2017，30（3）：345-348.

[7] 米晓丽，王鑫.一类潜伏期和染病期均传染的SEIR传染病模型的稳定性研究[J].山西师范大学学报：自然科学版，2016，30（3）：12-14.

[8] 赵海全，王美娟，唐春婷.潜伏期和染病期均传染的SEIS模型的分析[J].上海理工大学学报，2017，32（5）：457-460.

[9] 方彬，杨金根，李学志.潜伏期和染病期均具有康复的年龄结构MSEIS流行病模型的稳定性[J].应用数学，2018，22（1）：90-100.

[10] 马知恩，周义仓，李承治.常微分方程定性与稳定性方法[M].北京：科学出版社，2015：6.

[11] Huang SZ. A new SEIR epidemic model applications to the theory of eradication and control of diseases and to the calculation[J].Mathematical Bioscienc-es，2008，2015（1）：84-104.

[12] 郝林莉.几类具有潜伏期的流行病模型的稳定性分析[D].郑州大学，2019.

[13] 张瑞霞.基于动力系统的复杂社会网络中传播行为建模研究[D].山西大学，2018.

[14] Busenberg S，van den Driessche P. Analysis of a disease transmission model in a population with varying size[J].Journal of mathematical biology，2014，28（3）：257-270.