函数“零点差”问题的破解策略
2021-07-24四川省南充高级中学637000张小丹
四川省南充高级中学 (637000) 张小丹
函数是数学中的一个重要内.对于高中数学中的函数,我们常利用导数研究其性质,如单调性、极值、凹凸性等.数学中存在一些超越函数,其图像具备明显凹凸变化趋势,从而衍生出一类试题——零点差问题.
零点差问题的常见设问形式是证明函数f(x)的两个零点x1,x2满足|x1-x2|<φ(m).解决此问题的关键是找到两个数x1′,x2′,满足x1′≤x1 一般地,这两直线是函数y=f(x)在某点处的切线.有时题目会对两直线都有所提示;有时题目会提示其中一条直线,另一条直线需要通过分析待证不等式来获得.本文以几个典型题目为例,探究“左、右直线”的寻找,从而解决零点差问题. 例1 已知函数f(x)=xlnx. (1)求曲线y=f(x)在x=e-2处的切线方程; (2)关于x的不等式f(x)≥λ(x-1)在(0,+∞)上恒成立,求λ的取值范围; (3)关于x的方程f(x)=a有两个实数根x1,x2,求证:|x1-x2|<2a+1+e-2. 分析:易求得(1)y=-x-e-2;(2)λ=1;(3)实际上前两问就是为解决(3)而设置,即左直线为g(x)=-x-e-2,右直线为h(x)=x-1,且易证f(x)≥g(x),f(x)≥h(x). 图1 证明:设g(x)=-x-e-2,h(x)=x-1.易证f(x)≥g(x)(当且仅当x=e-2时取等号),易证f(x)≥h(x)(当且仅当x=1时取等号)(如图1).令g(x1′)=a,h(x2′)=a,解得x1′=-(a+e-2),x2′=a+1,∴x2′-x1′=2a+1+e-2.由g(x1′)=a=f(x1)≥g(x1),以及g(x)是减函数,得x1′≤x1(当且仅当a=e-2时取等号);由h(x2′)=a=f(x2)≥h(x2),以及h(x)是增函数,得x2≤x2′(当且仅当a=0时取等号),于是x1′≤x1 注:本题中左右直线分别为f(x)在x=e-2、x=1处的切线. 例2 已知函数f(x)=xlnx. (1)当x>0时,证明:f(x)≥-2x-e-3; 证明:(2)设g(x)=-2x-e-3,h(x)=x-1. 图2 注:本题中右直线为f(x)在x=1处的切线. 分析:易知f(x)先递减再递增,由于题目中没有出现任何一次函数,那么左、右直线如何确定呢?观察知f(x)的两个零点是-1和0,那么需要的两条直线是否为f(x)在这两个零点处的切线呢? 图3 注:本题中,左右直线分别为f(x)在x=-1、x=1处的切线. 图4 我们把“已知方程f(x)=m的两根为x1,x2(x1 一般地,(1)对于先增后减的曲线f(x),我们需要找到两条直线y=g(x)和y=h(x),使得g(x)≥f(x)≤h(x),其中g(x)是增函数,h(x)是减函数,如图5;令g(x1′)=h(x2′)=m,解得x1′、x2′,且x2′-x1′=φ(m).由g(x1′)=f(x1)≤g(x1)及g(x)是增函数可得x1′≤x1;由h(x2′)=f(x2)≤h(x2)及h(x)是减函数可得x2′≥x2′,于是|x1-x2|≤|x1′-x2′|=φ(m)(等号是否可取据实检查). (2)对于先减后增的曲线f(x),我们需要找到两条直线y=g(x)和y=h(x),使得g(x)≤f(x)≥h(x),其中g(x)是减函数,h(x)是增函数,如图6.令g(x1′)=h(x2′)=m,解得x1′、x2′,且x2′-x1′=φ(m).由g(x1′)=f(x1)≥g(x1),以及g(x)是减函数,得x1′≤x1;由h(x2′)=f(x2)≥h(x2),以及h(x)是增函数,得x2′≥x2′,于是|x1-x2|≤|x1′-x2′|=φ(m)(等号是否可取据实检查). 图5 图6一、切线放缩






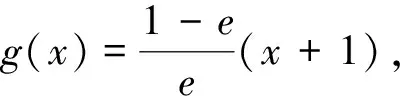


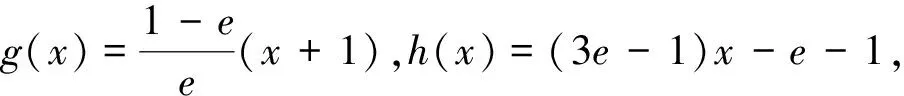
二、非切线放缩




三、反思与总结
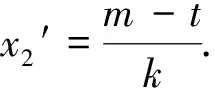

四、巩固练习




