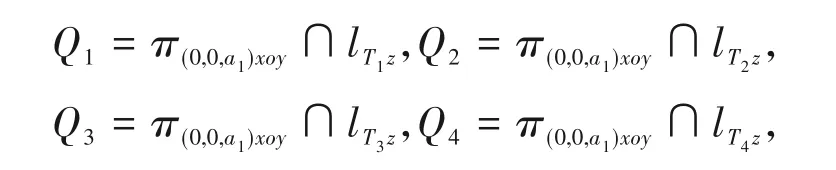杨 鎏，李长清

（1.陕西学前师范学院 数学与统计学院，陕西 西安 710100；2.闽南师范大学 数学与统计学院，福建 漳州 363000）

超空间理论一直是无限维拓扑学研究的热点。Curtis-Schori-West 超空间定理[1-4]是超空间理论乃至无限维拓扑学的一个基本定理：紧度量空间X中所有的紧集赋予Vietoris拓扑所构成的超空间同胚于Hilbert方体Q=[-1,1]ω当且仅当X是非平凡Peano连续统（连通的局部连通的紧的可分可度量空间）。超空间理论为无限维拓扑的研究提供了许多基本思想和方法，有学者将超空间理论中的一些方法应用于函数空间，创造了函数空间中许多有价值的结果[5-11]。

Nadler、Quinn以及Stavrokas[12]证明了以下结果：

定理A 设X是局部凸的可度量空间，cc(X)表示X上紧凸集全体赋予Hausdorff 度量拓扑所构成的超空间。

（1）如果X紧且dimX≥2，则cc(X)同胚于Q；

（2）如果n≥2，则cc(Rn)同胚于Q{0ˉ}；

（3）设U是Rn中的开凸集，n≥2，则cc(X)同胚于Q×[0,1)。

继Nadler等人的工作之后，许多学者还研究了Banach空间上有关闭凸集的各种超空间的拓扑结构[13-16]，更多有关底空间为线性空间的闭凸集超空间的介绍可参考文献[17]的引言部分。

杨鎏研究欧氏平面上定面积紧凸体的超空间的拓扑结构得到了关于Q-流形的刻画[17]，其中Q-流形定义为：若仿紧空间Y上存在一个开覆盖U，使得对任意的U∈U，存在开集V⊂Q使得U同胚于V，则空间Y被称为Q-流形[18]。

定理B 设v0> 0，Mv0为平面上所有面积为v0的紧凸体所构成的集族赋予Hausdorff 度量拓扑，则Mv0是一个Q-流形。

本研究讨论了定理B高维的版本，证明了下面的定理C。

定理C 设v0> 0，Mv0为三维欧氏空间中所有体积为v0的紧凸体所构成的集族，其上的拓扑为Haus⁃dorff度量拓扑，则Mv0同胚于一个Q-流形。设(X,d)是度量空间，E,F是X中的非空有界闭集，它们之间的Hausdorff距离定义为

本研究后面所提到的超空间若无特殊说明，其上的拓扑都为Hausdorff度量拓扑，A表示一个紧凸集。

1 预备知识

首先给出本研究一些常用的记号。

VA：A的体积。

int(A)：A的内部。

Bd(A)：A的边界，即Aint(A)。

Oδ(A) ={P∈R3|d(P,A) ≤δ)},δ> 0。

πPxoy：P经过点且平行于xoy面的平面。

cc(Rn)：n维欧氏空间的紧凸集全体构成的超空间。

ℑ：ℝ3中所有的紧凸体构成的超空间。

Mv0：ℑ中体积为正数v0的子超空间。

lPx：经过P点且平行于x轴的直线，相似的有记号lPy，lPz。

下面给出一些定义。

定义1.1 设X⊂R3，如果对X中任意两点a,b及t∈[0,1]，ta+(1-t)b∈X，则称X是R3中的凸集。如果凸集X的内部非空，则称X是凸体。

定义1.2[18]设(X,d)是度量空间，若对任意度量空间Y使得X是Y的闭子空间，存在连续映射r:Y→X使得r|X=idX，则称空间X是一个AR；若存在X在Y中的邻域U及连续映射r:U→X使得r|U=idX，则称空间X是一个ANR。

定义1.3 设A∈ℑ，TRA=RA1RA2RA3R A4RA5R A6RA7RA8是包含A的长方体，其中RAi=(rAix,rAiy,rAiz)是TRA的第i个顶点，i= 1,2,…,8，称TRA是A的正切长方体，如果TRA满足：

（1）rA1x=rA2x=rA7x=rA8x,rA3x=rA4x=rA5x=rA6x，rA1y=rA4y=rA5y=rA8y,rA2y=rA3y=rA6y=rA7y；

（2）rA4x≤rA1x，rA1y≤rA2y，rA8z≤rA1z，rA3x≤rA2x，rA7z≤rA2z，rA4y≤rA3y，rA6z≤rA3z，rA5z≤rA4z；

（3）rA1x-rA4x= max{x:(x,y,z) ∈A}- min{x:(x,y,z) ∈A}

=d(RA1,RA4)=d(RA2,RA3)=d(RA5,RA8)=d(RA6,RA7)，

rA2y-rA1y= max{y:(x,y,z) ∈A}- min{y:(x,y,z) ∈A}

=d(RA1,RA2)=d(RA3,RA4)=d(RA5,RA6)=d(RA7,RA8)，

rA1z-rA8z= max{z:(x,y,z) ∈A}- min{z:(x,y,z) ∈A}

=d(RA1,RA8)=d(RA2,RA7)=d(RA3,RA6)=d(RA4,RA5)。

注1.1 对任意的A∈ℑ，由正切长方体的定义可知

rA1x= sup{x:(x,y,z) ∈A},rA1y= inf {y:(x,y,z) ∈A},rA1z= sup{z:(x,y,z) ∈A}，

rA5x= inf {x:(x,y,z) ∈A},rA2y= sup{y:(x,y,z) ∈A},rA8z= inf {z:(x,y,z) ∈A}，

且rA4x

注1.2TRA∩A分别为πRAixoy、πRAiyoz、πRAizox上的紧凸集，i= 1,2,…,8，实际上，对于任意点P∈Bd(A)，过点P且垂直于xoy面的平面和A的边界之交为紧凸集。

命题1.1 设A∈ℑ，其对应的正切矩形为TRA=RA1RA2RA3RA4RA5RA6RA7RA8，则对任意的P∈intAxy，lPz和Bd(A)交于两个不同的点，其中DAxy表示A在xoy面的投影。

证明 设B=A∩πPxoy，则B是πPxoy上的紧凸体，再由文献[17]命题1得证。

对任意的P∈int(DAxy)，由命题1.1，可设lPz∩Bd(A) ={P1,P2}，且不妨设P1=(x,y,)，P2=(x,y,y)，再由注1.1可设

定义1.4 设A∈ℑ，令

则称fA和gA分别为区域DAxy上关于A的上半曲面函数和下半曲面函数。

注1.3 由命题1.1、注1.2和定义1.3可知fA和gA是由紧凸体A唯一确定的，即由A的边界唯一确定。

注1.4fA和gA在DAxy上连续。

定义1.6[19]设A是R3上的紧凸体，B是单位闭球，对任意的P∈A，令

以及

当SP包含Bd(A)且rout(P) -rin(P)的值最小时，就称对应的环为A的最小环，其对应的环心记为cA。

Bonnesen最早证明了平面上任意的一个紧凸体的最小环对应的环心是唯一确定的，实际上这个结果在高维的欧氏空间中也成立[20]。

定义1.7 设A∈ℑ，xoyz是R3上的右手直角坐标系。如果对每个P∈Bd(A)，存在一个右手直角坐标系x′o′y′z′使其为xoyz的一个正交变换，使得o′=cA,P=(0,0,β),β=d(cA,P)并且存在正数δ和一个定义在平面区域Dδxy上的连续函数f满足以下条件：

（1）f(0,0) =β；

（2）对任意的P0(x0,y0)∈Dδxy，(x0,y0,f(x0,y0)) ∈Bd(A)；

（3）f在P0(x0,y0)处的方向导数fl存在，则称A是可导的，P称为A的可导点。

注1.5 记空间中所有可导的紧凸体为ccon(X)，所有不可导的紧凸体为nccon(X)，则ccon(X) ∪nccon(X) = ℑ，ccon(X) ∩nccon(X) =φ。

注1.6 设B=π(0,0,γ)xoy∩A，则B将A分成两个共边界lπ(0,0,γ)xoy∩A的紧凸体A1和A2，并且对任意的P∈B是A1，A2的两个不可导点。

2 定理C的证明

定理2.1[21]一个局部紧的ANR(X,d)同胚于一个Q-流形当且仅当X满足以下条件：

对每个连续的函数ε:X→(0,∞)，分别存在两个连续的映射fε,gεX→X使得

（1）fε(X) ∩gε(X) = ∅；

（2）对每个x∈X,d(fε(x),x) ≤ε(x),d(gε(x),x) ≤ε(x)。

定理2.2[22]如果X是一个局部紧的度量空间，则X的子空间Y=F∩V也是局部紧的，其中F是X的闭子集，V是X的开子集。

引理2.1[18]Q{-0 }是ANR。

命题2.1 设A∈F,δ> 0，则：

（1）Oδ(A) ∈ℑ；

（2）Oδ:ℑ →ℑ连续；

（3）Oδ(A) ∈ccon(R3)。

命题2.2 设δ:ℑ →(0,+ ∞)是连续的函数，则：

（1）Oδ(A)(A) ∈ℑ；

（2）Oδ:ℑ →ℑ，Oδ(A) =Oδ(A)(A)连续。

命题2.3 设ε:Mv0→(0,+ ∞) 是连续函数。对任意的t∈[0,1)，定义ξt:Mv0→ℑ，ξt(A) ={(1-t)x|x∈Oε(A)(A)}，A∈Mv0。

（1）ξt是连续的映射；

（2）ξt(A)是可导的；

（3）存在tA∈(0,1)，使得VξtA(A) =v0；

（4）T:→(0,1),T(A) =tA是连续函数。

命题2.1、2.2、2.3的证明可参考文献[17]中命题4、5、7的证明。

最后，利用TorunczykQ-流形判定定理2.1证明定理C。

证明 首先，构造连续映射fε。对任意的A∈Mv0，不失一般性，不妨假设A在第一卦限。由命题2.3，存在tA∈[0,1)使得

令fε(A) =ξtA(Oε(A)/2(A))，显然dH(fε(A),A) ≤ε(A)/2。由命题3.3知，fε连续且fε(A)是可导的。

设以P1,P2,P3,P4,P′1,P′2,P′3,P′4为顶点的长方体为P。令A1=P∩A，A2=Aint(A1)，设α= min{z:(x,y,z) ∈Oε(A)(A)}。Oε(A)(A)的正切长方体的八个顶点仍记为ROε(A)(A)i,i= 1,2,…,8。令

记长方体T =T1T2T3T4T1′T2′T3′T4′={(x,y,z):rOε(A)4x≤x≤rOε(A)1x,rOε(A)4y≤y≤rOε(A)3y,α≤z≤a}，令A3=(T∩Oε(A)(A))A，如果VA1=VA3，令gε(A) =A2∪A3，由注1.6 可知任意的P∈Bd(πT1′xoy∩Oε(A)(A))是gε(A)的一个不可导点，分别记

其中a1由Vπ(0,0,a)xoy∩AVA+=v0所确定，A+={(x,y,z):(x,y,0) ∈DAxy,z∈[a1,rA1z]。

如 果VA1>VA3，令gε(A)=T1T2T3T4Q1Q2Q3Q4∩Oε(A)(A)，由 注 1.6 可 知 此 时 任 意 的P∈Bd(πQ1xoy∩Oε(A)(A))是gε(A)的不可导点。

如果VA1 0，使得VA4=v0，其中A4=Oδ0(A) ∩T。令gε(A)=A4，由注1.6 可知，此时任意的P∈Bd(πT3xoy∩Oε(A)(A))是gε(A)的不可导点，显然gε(A)连续。

由注1.5得fε(ℑ) ∩gε(ℑ) = ∅，

如果VF>v0，由命题2.3，存在tF∈(0,1)使得VOδF(F)=v0。如果VF 0使得VOδF(F)=v0。

显然r是连续的且r|Mv0是恒等。

由于ℑ是cc(R3)中的开集，再由定理A的结论（2）及命题2.1可知ℑ是ANR。对任意的可分可度量空间Y及它的闭子空间A、任意的连续映射f:A→Mv0，把f看成A到ℑ的连续映射。由于ℑ是一个ANR，则对A在Y上的邻域U存在连续邻域扩张:U→Q，则复合函数r∘:U→Mv0就是一个扩张，故Mv0是一个ANR。由定理A知cc(Rn)是局部紧的，再由定理2.2知它的开子集ℑ也是局部紧的，显然Mv0作为局部紧空间ℑ的闭子集也是局部紧的，最后由定理2.1证得结论成立。