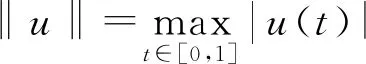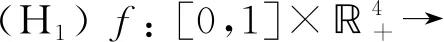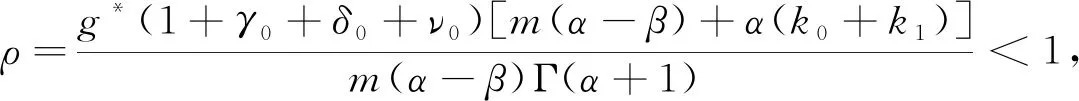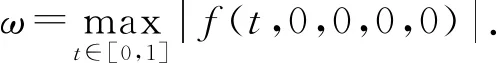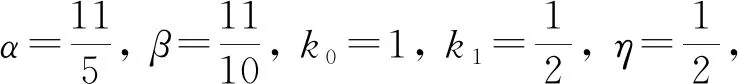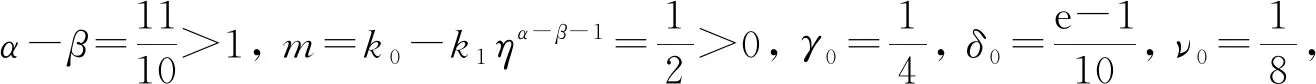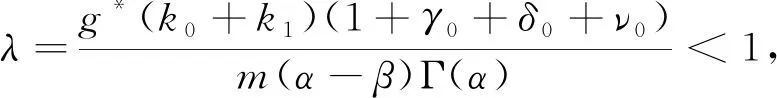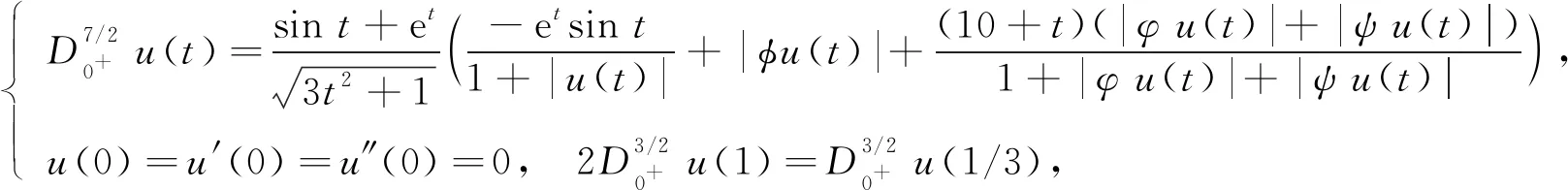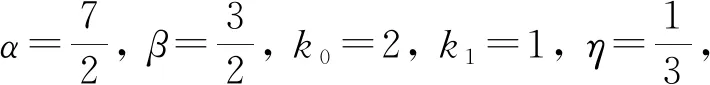一类非线性分数阶积分微分方程解的存在性与模拟仿真
2021-07-15孙文超苏有慧
孙文超, 苏有慧, 孙 爱
(1. 沈阳工业大学 理学院, 沈阳 110870; 2. 徐州工程学院 数学与统计学院, 江苏 徐州 221018)
0 引 言
微分方程问题在物理、 化学、 生物和工程等领域应用广泛[1-5], 目前, 关于分数阶微分方程解的存在性研究已有很多结果[6-12]. 但实际问题中抽象出的方程通常可能是较复杂的且含有积分的分数阶微分方程, 如扩散过程、 封闭系统中种群增长的Volterra模型及控制理论等[13-16]. 因此, 研究分数阶积分微分方程尤为重要.
文献[14]研究了如下分数阶积分微分方程正解的存在性:
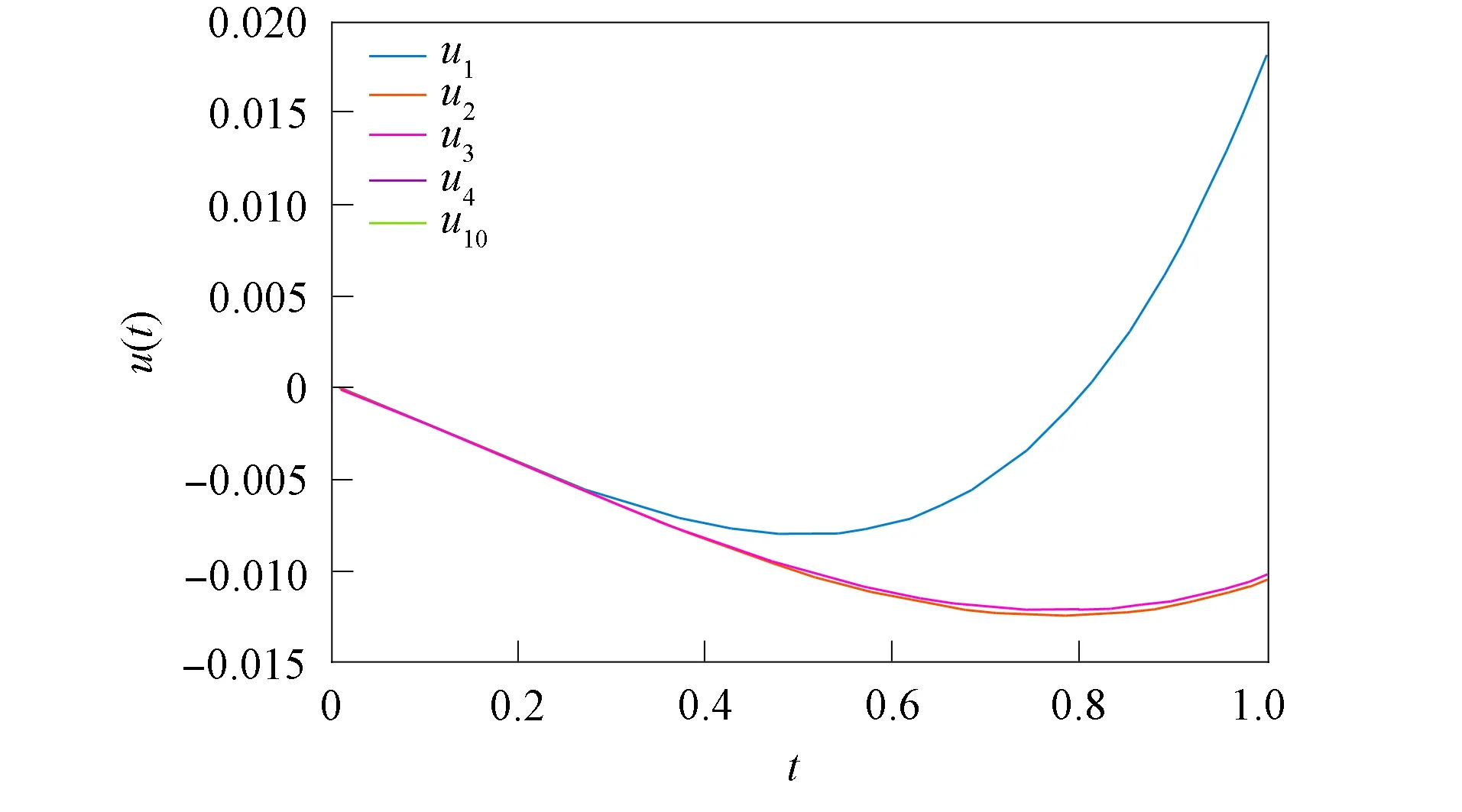
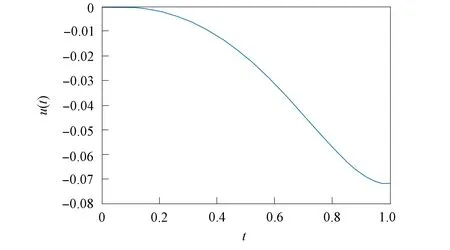
得到了其解的存在性和唯一性结果, 其中:n-1<α≤n, 0<μ 使用Krasnoselskii不动点定理, 得到了其至少存在一个解的结果, 其中: 1<α≤2, 0<β≤1;f: [0,1]×3→是连续的; 定义映射但上述结果都只从理论方面研究了分数阶积分微分解的存在性, 关于其数值解方面的研究目前报道较少[17-18].基于此, 本文考虑如下非线性分数阶积分微分方程: (1) 且满足 通过使用Banach压缩映射原理和Krasnoselskii不动点定理, 给出分数阶积分微分方程(1)至少存在一个解和存在唯一解的结论.特别地, 通过模拟仿真实例说明本文主要结果的正确性. 定义1[19]令α>0, 函数u: (0,+∞)→的Riemann-Liouville分数阶积分定义为 其中等式右端在(0,+∞)上有定义. 定义2[19]令α>0, 函数u: (0,+∞)→的Riemann-Liouville分数阶导数定义为 其中n-1≤α 引理1[20]令α>0, 则有分数阶微分方程 这里Ci∈,i=1,2,…,n,n=[α]+1. 引理2假设y∈C[0,1]且n-1<α (2) 有唯一解 (3) 这里m=k0-k1ηα-β-1>0. 证明: 根据引理1, 有 由u(0)=u′(0)=…=u(n-2)(0)=0, 可得 C2=C3=…=Cn-2=0, 因此 (4) 进一步可得 (5) 将式(5)代入式(4)即可推出式(3). 引理3(Krasnoselskii不动点定理)[21]设X是Banach空间E中的非空闭子集, 映射A,B满足如下条件: 1) 当x,y∈X时,Ax+By∈X; 2)A是连续且紧的; 3)B是一个压缩映射. 则存在z∈X, 使得z=Az+Bz. 假设: (H3) 存在一个常数b∈(0,α-n+1)和非负函数g(t)∈L1/b([0,1],(0,+∞)), 使得对任意的t∈[0,1],u,x,y,z,u′,x′,y′,z′∈, 均有 |f(t,u,x,y,z)-f(t,u′,x′,y′,z′)|≤g(t)(|u-u′|+|x-x′|+|y-y′|+|z-z′|). 定理1假设条件(H1)~(H3)成立, 且存在一个常数ρ, 如果 (6) 则边值问题(1)有唯一解. 证明: 定义算子A:X→X为 令ΩR={u∈X: ‖u‖ 1) 对任意的u∈ΩR,Au∈ΩR. 对u∈∂ΩR, 有 因此‖Au‖≤R, 从而A:ΩR→ΩR. 2)A是压缩映射. 对任意的u,v∈ΩR,t∈[0,1], 有 因此, |Au(t)-Av(t)|≤ρ‖u-v‖, 故A在ΩR上是压缩映射.根据Banach压缩映射原理可知, 边值问题(1)有唯一解. 例1考虑边值问题: (9) 根据定理1可知, 分数阶积分微分方程(9)有唯一解. 下面用迭代法对边值问题(9)进行模拟仿真, 并给出其迭代过程曲线与逼近解.令 θ(t)=f(t,u(t),φu(t),φu(t),ψu(t)), (10) 其中 取初始值 迭代公式为 边值问题(9)的迭代过程如图1所示.由图1可见, 其迭代过程是收敛的.图2是边值问题(9)经过10次迭代后的逼近解.由图2可见, 分数阶积分微分方程(9)有唯一解. 图1 边值问题(9)的迭代过程Fig.1 Iterative process of boundary value problem (9) 图2 边值问题(9)的逼近解Fig.2 Approximate solution of boundary value problem (9) 定理2假设条件(H1)~(H3)成立, 并且存在一个常数λ, 使得 (11) 则边值问题(1)在X中至少存在一个解. 证明: 先将ΩR上的映射A分成A1和A2, 其中 下面分为三步证明. 1) 对任意的x,y∈ΩR, 有A1x+A2y∈ΩR. 根据式(7)中倒数第二个不等式, 可得 对任意的x,y∈ΩR,t∈[0,1], 有 因此,A1x+A2y∈ΩR. 2)A1是连续且紧的. 首先, 证明A1在ΩR上一致有界.显然, 根据式(7)倒数第二个不等式的前两项, 有 因此, 对任意的u∈ΩR,A1在ΩR上一致有界. 其次, 证明A1是等度连续的.由于f是连续的, 易知A1也是连续的.令u∈ΩR,t1,t2∈[0,1], 且 可得 因此, 如果t2→t1, 则有 |(A1u)(t2)-(A1u)(t1)|→0, 故A1是等度连续的.根据Arzela-Ascoli定理可知,A1在ΩR中是连续且紧的. 3)A2是一个压缩映射. 对任意的u,v∈ΩR,t∈[0,1], 根据假设条件(H3), 有 由式(11)可知,A2是一个压缩映射.因此, 引理3所有的条件都满足, 故边值问题(1)至少存在一个解. 例2考虑边值问题: (12) 根据定理2可知, 分数阶积分微分方程(12)至少存在一个解. 下面利用迭代法对边值问题(12)进行模拟仿真, 并给出其迭代过程曲线与逼近解.令θ(t)定义如式(10), 其中 取初始值 迭代公式为 边值问题(12)的迭代过程如图3所示.由图3可见, 其迭代过程收敛.图4是边值问题(12)经过15次迭代后的逼近解.由图4可见, 分数阶积分微分方程(12)至少存在一个解. 图4 边值问题(12)的逼近解Fig.4 Approximate solution of boundary value problem (12)
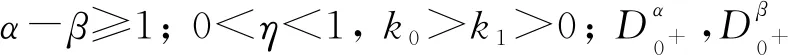
1 预备知识
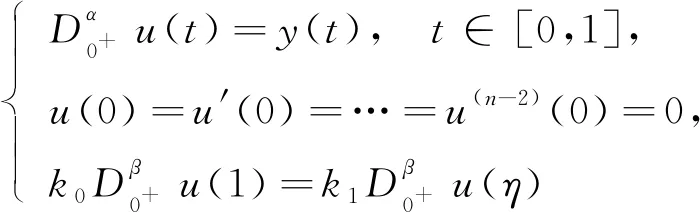

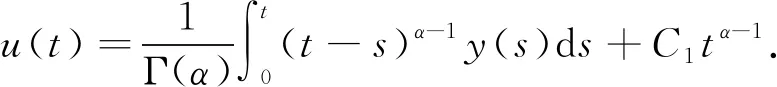
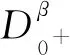

2 主要结果