贾秀卿, 李沐春

(兰州交通大学 应用数学研究所, 兰州 730070)

1 引言与主要结果

本文所讨论的图均为简单无向连通图.一个图G对应于一个有序三元组(V,E,φ), 其中V(G)表示图G的顶点集,E(G)表示图G中与V(G)不相交的边集,φ(G)表示图G顶点集与边集的关联函数, 使得对∀e∈E(G),u,v∈V(G), 有φ(e)=uv, 此时称u和v相邻,u和v是边e的两个端点, 同时也称u和v分别与e相关联.若图G中的两条边e1和e2仅有一个公共端点, 则称e1与e2相邻.与顶点x关联边的数目称为顶点x的度数, 记为d(x).称Δ(G)=max{d(x)|x∈V(G)}为图G的最大度, 简记为Δ.图G中度数为1的顶点称为悬挂点, 与悬挂点相邻的点称为次悬挂点.点u和v之间的距离定义为图G中最短的(u,v)路长, 记为d(u,v).一个边数等于点数的简单连通图称为单圈图.图G中最短圈的长称为图G的围长, 记为g(G).图G的一个正常k-边染色是指映射f:E→{1,2,…,k}, 使得对任意两条相邻的边e1和e2, 均有f(e1)≠f(e2).一个顶点x∈V在f下的色集合Sf(x)是指所有与x关联的边在f下的颜色构成的集合.

特别地, 当β=2时,D(β)-点可区别边染色称为D(2)-点可区别边染色.如果两个距离不超过2的顶点u,v在D(2)-点可区别边染色函数f下满足Sf(u)≠Sf(v), 则称u与v在f下是D(2)-点可区别的.

基于文献[9], 本文考虑单圈图在2-距离以内的D(2)-点可区别边染色.用数学归纳法并结合Hall定理, 得到如下结论:

定理1设G是围长为g的非圈单圈图,C是G中唯一的圈.如果G满足下列条件:

1) 当Δ(G)=3时, 圈上只有一个3度点,g≡0(mod 3)且次悬挂点在圈上; 或圈上有至少两个3度点且任意两个3度点的距离至少为3;

2) 当Δ(G)=4时, 任意两个4度点的距离至少为3且不包含如图1所示的S5作为子图;

图1 图S5Fig.1 Graph of S5

3) 当Δ(G)≥5时, 任意两个最大度点的距离至少为3.

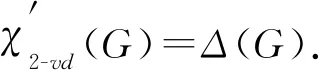
2 引 理

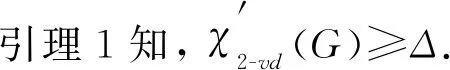
引理3[4]设Cp(p≥3)是一个阶数为p的圈, 则

引理5[4]对至少3阶的树T, 有

引理6(Hall定理)[10]设G为具有二分类(X,Y)的二部图, 则G包含饱和X的每个顶点的匹配当且仅当|N(S)|≥|S|对所有S⊆X成立.

引理7设G是围长为g的单圈图,Cg为G中唯一的圈.如果Δ(G)=3且圈Cg上仅有一个3度点, 则

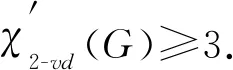
情形1)g≡0(mod 3).

若G的次悬挂点在圈Cg上, 则x必为G的悬挂点.设f1:E(G)→{1,2,3}为G的一个正常边染色.先用颜色1,3,2对边v1v2,…,vgv1进行循环染色, 然后用3色染边v1x.显然f1是G的一个3-D(2)-VDEC.

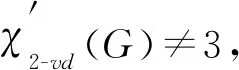
考虑如图2所示的图G1和G2, 其中图G1是圈Cg悬挂一条边v1x的单圈图, 图G2是一棵包含悬挂边v1x且最大度不超过3的树.

图2 图G1和G2Fig.2 Graphs of G1 and G2

注意到粘合图G1和G2中的边v1x可得到所需的图G.下面分别考虑图G1和G2的D(2)-VDEC.对于图G1, 因为其次悬挂点恰好在圈上, 故染色f1是G1的一个3-D(2)-VDEC.对于图G2, 由引理5知, 4种色可以对其进行D(2)-VDEC, 记该染色方案为f2.不妨设f2(v1x)=3,f2(xw1)=4.若w2存在, 不妨设f2(xw2)=1, 再用{2,4}中的颜色染它的其余关联边.

为证明图G是4色可染的, 只需验证图G1和G2在上述染色方案不变的条件下粘合边v1x后仍满足2距离之内的点的色集合不同即可.定义图G的一个正常边染色f*为: 对于∀z∈E(G),

根据f*的构造可知,

S(v1)={1,2,3},S(v2)={1,3},S(vg)={2,3},

而4∈S(x)∩S(w1), 所以S(x)≠S(v1)≠S(vg)≠S(v2)且S(w1)≠S(v1).如果w2存在, 若dG2(w2)=2, 由于dG(v1)=3, 故S(w2)≠S(v1); 若dG2(w2)=3, 由染色f2知S(w2)={1,2,4}, 故S(w2)≠S(v1).此外,G中的其他点各自在f1与f2下色集合保持不变, 所以仍然满足D(2)-点可区别.故f*是图G的一个4-D(2)-VDEC.

情形2)g≢0(mod 3).

当图G中次悬挂点在圈Cg上时, 用颜色1,2,3对边v1v2,…,vg-2vg-1进行循环染色; 分别用颜色4,2,3染边vg-1vg,vgv1,v1x.由该染色方案知,v2,v3,…,vg-4的色集合依次循环等于{1,2},{2,3},{1,3}, 且vg-3,vg-2,vg-1,vg,v1的色集合分别为{1,2},{2,3},{3,4},{2,4},{1,2,3}.易见G中的点都是D(2)-点可区别的.

当图G中次悬挂点不在圈Cg上时, 证明与g≡0(mod 3)类似, 故略.

注1引理7中, 若圈Cg上仅含一个3度顶点且g≡1(mod 3), 则可得文献[8]中定理3.11(3).因此, 引理7在一定程度上可视为文献[8]中定理3.11(3)的推广.

引理8设G是围长为g的非圈单圈图且GS5(见图1),C是G中唯一的圈,G中次悬挂点都在圈上.如果G满足下列条件:

1) 当Δ(G)=3时, 圈上只有一个3度点且g≡0(mod 3); 或圈上有至少两个3度点且G中3度点之间的距离至少为3;

2) 当Δ(G)≥4时,G中最大度点之间的距离至少为3.

证明： 令C=v1v2…vgv1.约定i=1时,vi-1表示点vg.令E(vi)E(C)表示与vi关联的不在圈上的边.下面分四步完成证明.

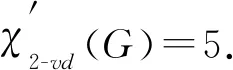
图3 图S5的5-D(2)-点可区别边染色Fig.3 5-D(2)-VDEC of graph of S5

2) 证明GS5时下面根据围长g分两种情形讨论.

情形①g≠5.

首先对E(C)进行染色, 记染色方案为ψ1.按顺时针方向, 当g≡0(mod 3)时, 用颜色1,2,3依次对边v1v2,…,vgv1进行循环染色; 当g≡1(mod 3)时, 用颜色1,2,3依次对边v1v2,…,vg-1vg进行循环染色, 用颜色4染边vgv1; 当g≡2(mod 3)时, 用颜色1,2,3依次对边v1v2,…,vg-5vg-4进行循环染色, 用颜色4,1,2,3,4依次对边vg-4vg-3,…,vgv1进行循环染色.

其次对E(G)E(C)进行染色, 记染色方案为ψ2.在色集合

{1,2,…,Δ+1}{ψ1(vi-1vi),ψ1(vivi+1),ψ1(vi+1vi+2)}

中选取颜色正常染色E(vi)E(C).

注意到在染色ψ1下, 对∀i(1≤i≤g), 有vi-1vi,vivi+1,vi+1vi+2三边不同色.又由染色ψ2知,ψ1(vi+1vi+2)∉S(vi), 而ψ1(vi+1vi+2)∈S(vi+1)∩S(vi+2), 故该染色可将vi与vi+1,vi+2的色集合区分开.因此该染色是图G的一个D(2)-VDEC.

情形②g=5.

当Δ=3时, 由于GS5, 所以至多有4个3度点.注意到因此, 圈C上3度点是4色D(2)-点可区别的.当Δ≥4时.先用颜色1,2,3,4,5依次染C上的边v1v2,…,v5v1, 再从{1,2,…,Δ+1}除去vi-1vi,vivi+1,vi+1vi+2三边所染颜色后得到的色集合中选取颜色正常染色E(vi)E(C).易见该染色能使得G中2-距离以内的点的色集合可区别.

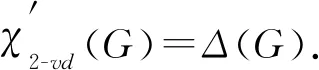
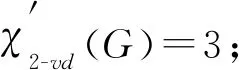
情形①g≡0(mod 3).

设f1:E(C)→{1,2,3}是一个正常边染色.用颜色1,2,3按顺时针方向依次循环染色v1v2,…,vgv1.设f2:E(G)E(C)→{1,2,3}是一个正常边染色.对∀x∈E(vi)E(C),f2(x)=α, 其中α满足

{f1(vi-1vi),f1(vivi+1),α}={1,2,3}.

在f1和f2不变的条件下, 定义图G的一个正常边染色f*为

显然3度点与2度点是D(2)-点可区别的.此外, 由于3度点之间的距离至少为3, 故其色集合可以相同.对于v2,…,vg,v1, 其在f1下的色集合依次循环为{1,2},{2,3},{1,3}, 故v1,…,vg中的2度点也是D(2)-点可区别的.因此,f*即为图G的一个3-D(2)-VDEC.

情形②g≢0(mod 3).

当g≡1(mod 3)时.设G′是圈上恰有两个3度点的此类单圈图, 不妨设d(v1)=d(vm)=3, 其中d(v1,vm)≥3.首先对E(C)进行染色.设染色函数φ1:E(C)→{1,2,3}.按逆时针方向, 用颜色1,2,3依次对边v1vg,vgvg-1,…,vm+1vm进行循环染色; 对边vmvm-1,vm-1vm-2,…,v2v1, 当d(v1,vm)≢2(mod 3)时, 用颜色2,1,3依次循环染色, 否则用1,3,2依次循环染色.

其次对E(G′)E(C)染色.设染色函数φ2:E(G′)E(C)→{1,2,3}.对∀x∈E(vi)E(C),φ2(x)=α, 其中α满足

{φ1(vi-1vi),φ1(vivi+1),α}={1,2,3}.

易知φ2是一个正常边染色.注意到在φ1下, 当d(v1,vm)≡0(mod 3)时, 边v1vg,v2v1,vm+1vm,vmvm-1分别染颜色1,3,1,2; 当d(v1,vm)≡1(mod 3)时, 其分别染颜色1,2,3,2; 当d(v1,vm)≡2(mod 3)时, 其分别染颜色1,3,2,1.故v1vg与v2v1不同色, 且vm+1vm与vmvm-1不同色.又显然C上其余边也满足相邻边染不同色, 所以φ1是C的一个正常边染色.在φ1和φ2保持不变的条件下, 定义图G′的一个正常边染色φ*为

显然3度点与2度点是D(2)-点可区别的.由染色φ*知, 对于vg,vg-1,…,vm+1, 其色集合依次循环为{1,2},{2,3},{1,3}, 故其为D(2)-点可区别的.对于vm-1,vm-2,…,v2, 当d(v1,vm)≢2(mod 3)时, 其色集合依次循环为{1,2},{1,3},{2,3}, 否则循环为{1,3},{2,3},{1,2}, 故其也是D(2)-点可区别的.对于vm+1,vm-1, 当d(v1,vm)≡0(mod 3)时, 其色集合分别为{1,3},{1,2}; 当d(v1,vm)≡1(mod 3)时, 其色集合分别为{2,3},{1,2}; 当d(v1,vm)≡2(mod 3)时, 其色集合分别为{1,2},{1,3}.故vm+1与vm-1可区别.又S(vg)={1,2},S(v2)={1,3}或{2,3}, 故vg与v2也可区别.因此, 2度点与2度点也满足D(2)-点可区别.

设G是满足上述条件且至少有3个3度点的单圈图, 则G′⊆G.根据上述证明可知:φ*是图G′的一个3-D(2)-VDEC.由于图G是由其子图G′通过在圈C上添加悬挂边构成的, 故对图G进行染色时, 先用φ*对E(G′)进行染色; 再从色集合{1,2,3}中选取颜色正常染新添加的悬挂边.易见, 此时G中的点仍然满足D(2)-点可区别.因此3种颜色可以对图G进行D(2)-VDEC.

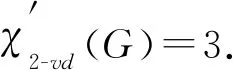
(ii) 当Δ≥4且G中最大度点之间的距离至少为3时, 根据围长g分两种情形讨论.

情形①g≠5.

设φ1:E(C)→{1,2,…,Δ}是一个正常边染色.用染色ψ1染圈C.设φ2:E(G)E(C)→{1,2,…,Δ}是一个正常边染色.当d(vi)=Δ时, 用色集合{1,2,…,Δ}{φ1(vi-1vi),φ1(vivi+1)}中的颜色正常染E(vi)E(C); 当3≤d(vi)≤Δ-1时, 用色集合{1,2,…,Δ}{φ1(vi-1vi),φ1(vivi+1),φ1(vi+1vi+2)}中的颜色正常染E(vi)E(C).在φ1和φ2保持不变的条件下, 定义图G的一个正常边染色φ*为

显然两个度数不同的点是D(2)-点可区别的.此外, 由于最大度点之间的距离至少为3, 故其色集合可以相同.对于∀i(1≤i≤g), 在染色φ1下, 有vi-1vi,vivi+1,vi+1vi+2三边不同色.当d(vi)<Δ时, 由φ2知,φ1(vi+1vi+2)∉S(vi), 而φ1(vi+1vi+2)∈S(vi+1)∩S(vi+2), 故vi与vi+1,vi+2的色集合可区别.因此φ*是图G的一个Δ-D(2)-VDEC.

情形②g=5.

首先对E(C)染色.当Δ=4时, 不妨设d(v1)=4, 用颜色1,2,3,4,2依次染v1v2,…,v5v1; 当Δ≥5时, 用颜色1,2,3,4,5依次染v1v2,…,v5v1.然后对E(G)E(C)染色.若d(vi)=Δ, 用{1,2,…,Δ}除去vi-1vi,vivi+1两边所染颜色后得到的色集合中颜色正常染色E(vi)E(C); 当3≤d(vi)≤Δ-1时, 从{1,2,…,Δ}中除去vi-1vi,vivi+1,vi+1vi+2三边所染颜色后得到的色集合中选取颜色正常染色E(vi)E(C).易见该染色可使得G中2-距离以内的点的色集合不同.

4) 证明GS5且不满足下列条件时有

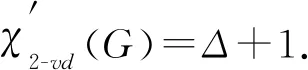
3 定理1的证明

下面证明定理1.设C=v1v2…vgv1为单圈图G中唯一的圈.对任意v∈V(G), 若d(v)≥2且v∉V(C), 则称v为图G的内点, 记图G的内点个数为p.对任意一个悬挂点x, 设d(x,C)=min{d(x,u)|u∈V(C)}, 令x0是满足d(x0,C)=max{d(x,C)}的一个悬挂点.设v是x0的邻点, 则v只有一个邻点w是非悬挂点.令d(v)=k, 其中k≥2.设x1,x2,…,xk-2是v的除w和x0处的邻点(如果有), 则有

d(x0)=d(x1)=…=d(xk-2)=1.

设y1,y2,…,yd(w)-1是w的除v处的邻点, 不妨设y1是在圈C到x0的最长路上.

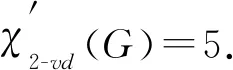
证明： 对p利用数学归纳法.当p=0时, 由引理8知结论成立.假设结论对内点个数小于p时均成立.设G有p(p≥1)个内点.令G′=G-{x0,x1,…,xk-2}, 其中k≤Δ.由归纳假设知, (Δ+1)种色(不妨记色集合为S={1,2,…,Δ+1})可以对图G′进行D(2)-VDEC, 记染色方案为f′.不妨设f′(y1w)=Δ+1.令y2,y3,…,yt是G中与v的度数相等的点.设f′(wv)=c1,f′(wyi)=ci, 其中2≤i≤t.下面根据k分两种情形将f′延拓为图G的一个D(2)-点可区别边染色f.

情形1)k<Δ.

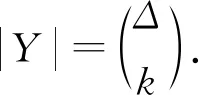
矛盾.因此T在Y中至少有l个相邻点.由引理6知, 此时存在一个匹配能够饱和X中的点.从而可选取满足f(wv)=c1的一个色集合Aj中的颜色去染色与v关联的边, 使得v与y2,y3,…,yt的色集合可区别.又因为Δ+1∈Sf(w)∩Sf(y1), 而Δ+1∉Sf(v), 故v与y1,w的色集合也可区别.

情形2)k=Δ.

设a,b是两种颜色, 使得a∉S(y1)且b∉S(w).为保证正常边染色, 则wv,wyi(2≤i≤t)中至少有(t-1)条边不染色a.不妨设为wv,wy2,…,wyt-1.下面在染色f′的基础上, 通过对v的关联边进行染色并重新染与y2,y3,…,yt关联的边构造染色f.首先令f(wv)=c1,f(wyi)=ci(2≤i≤t); 其次用色集合S{c2}中的颜色正常染v的其余关联边, 用S{ci+1}中的颜色正常染yi(2≤i≤t-2)的其余关联边, 用S{c1}中的颜色正常染yt-1的其余关联边, 用{1,2,…,Δ}中的颜色正常染yt的其余关联边.由于

{a,b,Δ+1}⊆Sf(v)∩Sf(yi)(2≤i≤t-1), {a,b}⊆Sf(yt),

而a∉Sf(y1),b∉Sf(w),Δ+1∉Sf(yt)且c1≠c2≠…≠ct, 故v,w,yi中的点满足D(2)-点可区别.

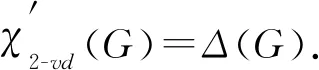
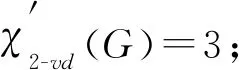
当Δ≥5时, 若最大度点之间的距离至少为3, 则p=0时, 由引理8知结论成立.假设结论对内点个数小于p时均成立, 设G有p(p≥1)个内点, 于是G′有一个色数为Δ(不妨记色集合为S={1,2,…,Δ})的D(2)-点可区别边染色f′.令y2,y3,…,yt是G中与v的度数相等的点.设f′(wv)=c1,f′(wyi)=ci(2≤i≤t).下面根据k分3种情形将f′延拓为图G的一个D(2)-点可区别边染色f.

情形1) 2≤k<Δ-1.

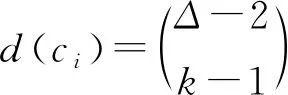
矛盾.故T在Y中至少有l个相邻点.由引理6知, 存在一个匹配能够饱和X中的点.此时选取满足f(wv)=c1的一个色集合Aj中的颜色去染与v关联的边.

情形2)k=Δ-1.

当d(w)=Δ时, 有d(y1)<Δ.设a∈{1,2,…,Δ}S(y1).由于d(w)=Δ, 故色a一定出现在w的色集合中.不妨设f′(wyt)=a, 则边wv,wy2,…,wyt-1不染色a.下面在染色f′的基础上, 通过对v,y2,…,yt的关联边进行染色构造染色f.首先令f(wv)=c1,f(wyi)=ci(2≤i≤t); 其次用色集合S{c2}中的颜色正常染v的其余关联边, 用S{ci+1}中的颜色正常染yi(2≤i≤t-2)的其余关联边, 用S{c1}中的颜色正常染yt-1的其余关联边, 用S{f′(wy1)}中的颜色正常染yt的其余关联边.由于a∈Sf(v)∩Sf(yi)(2≤i≤t-1), 而a∉Sf(y1), 故f可使得v,yi中的点是D(2)-点可区别的.

当d(w)<Δ时.类似地可得图G的一个Δ-D(2)-VDEC.

情形3)k=Δ.

显然v,w,yi中只有v是最大度点, 用色集合S中的颜色正常染v的关联边即可.

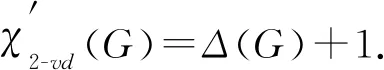
综上所述, 定理1得证.