钱 蓉, 肖 敏, 王 璐

(南京邮电大学 自动化学院, 人工智能学院, 南京 210023)

0 引 言

传染病的传播严重威胁人类的生命安全, 如目前全球传染规模最大的COVID-19(corona virus disease 2019, 新型冠状病毒肺炎). 由于传染病的研究不能通过大规模的实验进行, 因此建立具有传染病典型特征的数学模型, 进行传染病动力学分析, 探索传染病传播规律, 并预测其发展趋势是对传染病进行预防和控制的有效方法之一[1]. 自Kermack等[2]提出经典的SIR(susceptible-infected-removed)模型以来, SIR传染病模型在传染病动力学分析中备受关注. 时滞对系统动力学有较大影响, 其可以破坏系统的稳定性, 诱发更复杂的动力学行为, 如周期振荡、 分岔或混沌[3]. 在多数情况下, 传染病患者康复后会产生抗体, 再次感染的机率很小, 因此本文研究的SIR模型考虑患者康复后不再受到感染, 主要研究病毒潜伏期时滞的影响.

分数阶微积分是由经典微积分到非整数阶微积分的推广[4], 近年来, 因其在化学、 混沌和分形、 控制系统等领域中的应用而受到广泛关注[5], 分数阶微分方程为描述各种过程的记忆和遗传特性提供了一个强有力的工具[6]. 文献[7]研究了一类时滞分数阶捕食者-食饵模型, 以时滞为分岔参数讨论了该模型的Hopf分支问题； 文献[8]基于一类分数阶生态流行病学模型, 研究了该模型解的性质和平衡点的稳定性. 但目前已有的分数阶传染病模型研究都假设分数阶次一致, 未进一步考虑不同阶次下分数阶传染病模型的动力学性质. 而阶次不一致的分数阶系统在控制领域已得到广泛关注[9], 研究表明, 不同阶次的分数阶系统中存在更多的自由度[10], 使系统的动力学行为更复杂. 目前大多数研究者在建立传染病模型时都假设易感者人数为一个恒定输入, 但一旦爆发疫情, 各地区的易感人群数量不会是恒定增长的, 因此本文假设易感人群数量满足Logistic增长, 更符合实际意义[11]. 由于单位时间内一个感染者接触到易感者的数量有限, 故传统建模中采用的标准传染率和双线性传染率[12]不能准确描述传染病的传播特性, 因此, 不同形式的非线性传染率被相继引入到传染病模型中[13]. 文献[14]将饱和传染率g(I)S引入到传染病建模中, 为人们研究传染病模型提供了一种新思路； 文献[15]引入了一种标准饱和传染率βSI/(S+I+R), 但并未考虑感染者和易感者接触的随机性; 文献[16]通过引入饱和传染率βSI/(1+αS), 研究了具有饱和传染率的分数阶SIR传染病模型的稳定性, 该饱和传染率不但考虑了感染者聚集对传染病传播的影响, 并且通过选取适当的参数α, 可调节感染者和易感者的接触率.因此, 采用饱和传染率βSI/(1+αS)建立SIR传染病数学模型能更好地描述传染病传播的实际情况[17]. 本文研究一类具有Logistic增长与饱和传染率的不同阶次分数阶时滞SIR传染病模型的稳定性和分岔分析.

1 预备知识

1.1 分数阶导数的定义

目前, 分数阶导数定义主要有Riemann-Liouville(R-L)定义、 Caputo定义和Grünwald-Letnikov(G-L)定义. 不同定义下的分数阶导数各有特点, 其中Caputo定义允许将分数阶方程的初始条件以整数阶导数的形式表示, 更适合实际问题的数学建模[18]. 因此本文选取Caputo导数定义处理SIR传染病模型.

定义1[19]连续函数f(t)的α阶Caputo导数定义为

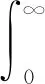
1.2 系统稳定性判据

引理1[20]考虑如下形式的分数阶系统：

(1)

其中α∈(0,1],x(t)∈n.如果系统的特征值λi均具有负实部或满足条件|arg(λi)|>(αiπ)/2, 则系统的平衡点是局部渐近稳定的[21].

α阶系统的稳定区域如图1所示, 因此分数阶系统比整数阶系统的稳定域更大.

图1 分数阶系统的稳定区域Fig.1 Stable region of fractional-order system

2 模型的建立

文献[22]研究了一类考虑时滞与饱和传染率的整数阶SIR传染病模型：

(2)

其中：S(t),I(t),R(t)分别表示t时刻易感者、 感染者和康复者的数量；xS(t)(1-S(t)/y)表示易感患者人数满足Logistic增长,x表示内在增长率,y表示系统承载力； 时滞τ表示病毒传播的潜伏期, (mS(t)I(t-τ))/(1+nS(t))表示在t-τ到t时间段内感染的患者数量,m表示病毒传染率,n表示感染者和易感者的接触率；a表示感染患者的因病死亡率,b表示传染病康复率,c表示自然死亡率.由生态学意义可知, 系统(2)所有参数均为非负常数.

相对于传统模型, 模型(2)综合考虑了时滞的影响及传染病传播的生物学特性.文献[22]以时滞τ为分岔参数分析了系统(2)的稳定性, 并讨论了系统Hopf分岔的存在性. 但这些分析都基于整数阶系统, 缺少人口模型的记忆特性. 本文在模型(2)的基础上, 考虑到Logistic增长与饱和传染率, 通过引入不同阶次下的分数阶模型, 建立一类新型时滞SIR传染病模型：

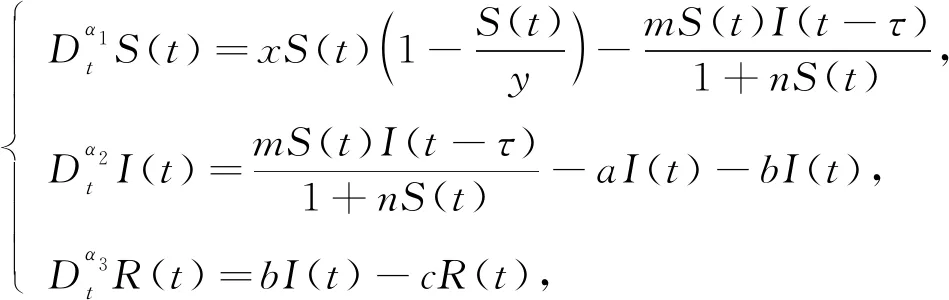
(3)

其中0<αi≤1(i=1,2,3).系统(3)满足初始条件：S(θ)=φ1(θ)≥0,I(θ)=φ2(θ)≥0,R(θ)=φ3(θ)≥0,θ∈[-τ,0].

3 平衡点及稳定性分析

3.1 系统解的非负性

定理1若S(0),I(0),R(0)是系统(3)的非负初始条件, 则系统(3)的解S(t),I(t),R(t)对所有的t∈[0,+∞)都是非负的.

证明： 根据系统(3)的第一和第二个方程, 结合一阶线性方程求解法, 可得

根据系统(3)的第三个方程可得

因此, 若初始条件满足S(0),I(0),R(0)都是非负数, 则对所有的t∈[0,+∞)系统的可行解都是非负的.

3.2 平衡点的局部稳定性分析

3.2.1 平衡点及基本再生数

平衡点就是当改变系统变量时, 系统状态不随其变化的时刻.因此分数阶系统平衡点的定义和整数阶一致.以系统(1)为例, 分数阶系统的平衡点通过求解f(t,x(t))=0计算.

计算求得系统(3)的平衡点为E=(S′,I′,R′), 其中平凡平衡点为E0=(0,0,0), 无病平衡点为E1=(y,0,0), 地方病平衡点为E2=(S*,I*,R*), 且

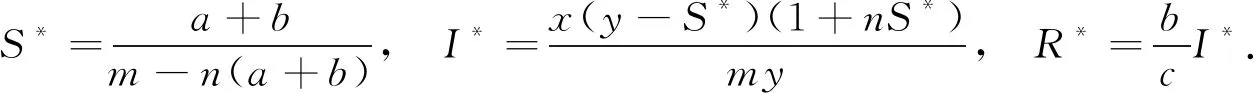
(4)

基本再生数R0是决定传染病能否得到控制的阈值, 根据感染仓理论可知,R0只与身体内携带病毒的感染者数量I(t)有关, 本文采用文献[23]中的第二代生成矩阵法计算得到无病平衡点E1处的基本再生数.再生矩阵

其在无病平衡点E1=(y,0,0)处的Jacobi矩阵为

因此系统(3)的基本再生数为

定理2若R0>1, 则系统(3)存在唯一的地方病平衡点E2=(S*,I*,R*)； 若R0<1, 则系统(3)不存在地方病平衡点.

证明： 由于地方病平衡点满足式(4), 所以当R0>1时,my>(1+ny)(a+b)>ny(a+b), 即m>n(a+b), 从而可知S*>0, 对于I*考虑

显然此时I*>0,R*>0, 即系统(3)存在唯一的地方病平衡点； 而当R0<1时,S*<0, 即系统(3)不存在地方病平衡点.证毕.

3.2.2 无病平衡点的局部稳定性分析

由于本文模型中康复患者的数量R(t)对易感人群的数量S(t)和已感染人群的数量I(t)均无影响, 系统的动力学行为主要由系统(3)的前两个方程决定, 因此为讨论方便, 本文将系统(3)简化为

(5)

为分析系统的局部渐近稳定性, 将系统(5)线性化得到平衡状态下的线性系统：

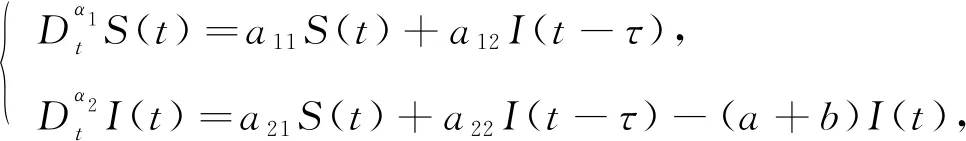
(6)

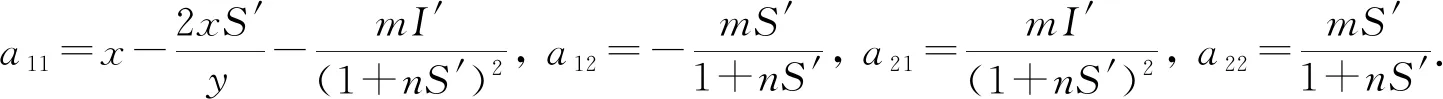
令S1(t)=S(t)-S′,I1(t)=I(t)-I′, 将系统(6)的平衡点移动到原点, 并进行Laplace变换, 得

(7)

其中L[f(t)]表示对f(t)的Laplace变换.系统(7)可以写成如下形式：

(8)

其中

令det(Δ(s))=0可得系统(3)的特征方程为

μ1(s)+μ2(s)e-sτ=0,

(9)

其中μ1(s)=sα1+α2+(a+b)sα1-a11sα2-a11(a+b),μ2(s)=-a22sα1-a12a21+a11a22.

将平凡平衡点E0=(0,0,0)代入方程(9)计算可得特征方程为

(λ1-x)(λ2+a+b)=0,

(10)

其中λ1=sα1,λ2=sα2,x,a,b均为是非负数.显然平凡平衡点E0=(0,0,0)是一个不稳定的鞍点.所以本文下面主要讨论无病平衡点E1=(y,0,0)和地方病平衡点E2=(S*,I*,R*)的稳定性.

定理3若R0<1, 则当τ=0时, 系统(3)的无病平衡点E1=(y,0,0)是局部渐近稳定的.

证明： 计算可得系统(3)在无病平衡点E1=(y,0,0)处的特征方程为

(11)

当τ=0时, 方程(11)转化为

(12)

令λ1=sα1,λ2=sα2, 系统的特征根为

λ1=-x,λ2=my/(1+ny)-(a+b)=(a+b)(R0-1),

显然可知, |arg(λ1)|=π>α1π/2.当R0<1时, |arg(λ2)|=π>α2π/2, 根据引理1可知, 系统(3)的无病平衡点E1局部渐近稳定, 证毕.

定理4若R0<1, 则对任意的τ≥0, 系统(3)的无病平衡点E1=(y,0,0)是局部渐近稳定的.

证明： 当R0<1时, 定理3成立.因为方程(11)中只有sα2含有时滞项, 因此只需考虑当τ>0时, 方程

(13)

根的分布情况.假设方程(13)存在一对纯虚根s1,2=±iω(ω>0), 将s1=iω代入方程(13)得

(14)

对方程(14)分离实部、 虚部可得

(15)

将式(15)两边平方并相加整理可得

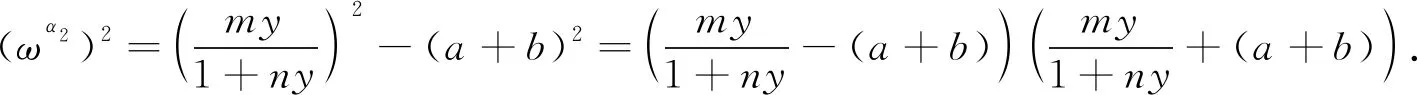
(16)

显然, 当R0<时式(16)不成立, 即方程(13)不存在纯虚根, 再结合定理3及特征根关于时滞的连续性可知, 当R0<时, 对于任意的τ≥0, 系统(3)的无病平衡点E1都是局部渐近稳定的.证毕.

注1定理4表明, 当基本再生数R0<时, 时滞对系统(3)的稳定性无影响.

3.2.3 地方病平衡点的局部稳定性分析

根据方程(9)可知, 地方病平衡点E2=(S*,I*,R*)处的特征方程为

sα1+α2+(a+b)sα1-a11sα2-a11(a+b)+(-a22sα1-a12a21+a11a22)e-sτ=0.

(17)

定理5若α1,2∈(0,1],R0>1, 则当τ=0,a11<0且a+b-a22>0时, 系统(3)的地方病平衡点E2局部渐近稳定.

证明： 由定理2可知, 当R0>1时, 系统(3)才存在地方病平衡点, 且当时滞τ=0时, 特征方程(17)可以改写为

sα1+α2+(a+b-a22)sα1-a11sα2-a11(a+b)-a12a21+a11a22=0.

(18)

由于无法通过直接计算得到方程(18)的根, 所以本文采用反证法, 证明该特征方程的特征根均具有负实部.

首先, 将s=0代入特征方程(18), 等式不成立, 即特征方程(18)没有零根.

其次, 假设特征方程(18)有正实根或纯虚根记为Xeθi, 其中X>0,θ∈[-π/2,π/2].将s=Xeθi代入方程(18), 并分离实部和虚部, 得

Xα1+α2[sin(θα1+θα2)]+(a+b-a22)Xα1sin(θα1)-a11Xα2sin(θα2)=0,

(20)

分析方程(20)发现： 三项正弦函数前系数满足Xα1+α2>0, (a+b-a22)Xα>0, -a11Xα>0.因此方程(20)左侧公式的符号和sinθ符号一致.

当且仅当θ=0时方程(20)成立, 将θ=0代入方程(19),a12a21=-m2SI/(1+nS)3<0, 可得

Xα1+α2+(a+b-a22)Xα1-a11Xα2-a11(a+b-a22)-a12a21>0,

即θ=0不满足方程(19).方程组(19)-(20)无解, 原假设不成立, 即特征方程(18)没有正实部根或纯虚根.再结合引理1, 结论得证.

3.3 Hopf分岔

本文选取时滞τ为分岔参数讨论系统地方病平衡点的分岔情况.根据Hopf分岔定理[24]可知, 若使系统发生Hopf分岔, 则需系统在平衡点处对应的特征方程有一对共轭复根ρ(τ)±iω(τ), 且在τ=0时该共轭复根满足ρ(0)=0,ω(0)=ω0>0, 并满足横截条件ρ′≠0, 即ρ(τ)±iω(τ)轨迹在τ=τ0处横穿虚轴.

定理6若R0>1,a11<0,a+b-a22>0,ω存在且P1Q1+P2Q2>0成立, 则：

1) 当τ<τ0时, 系统(3)的地方病平衡点E2是局部渐近稳定；

2) 当τ>τ0时, 系统(3)的地方病平衡点E2不稳定, 即系统(3)在τ=τ0附近发生Hopf分岔.

证明： 假设当τ≥0时, 特征方程(9)存在一对纯虚根s1,2=±iω(ω>0), 将s=iω=ωe(πi)/2代入方程(9), 得

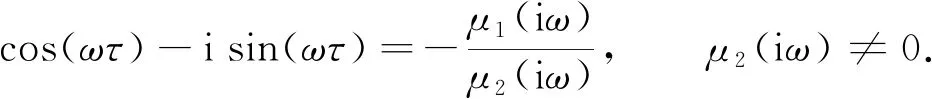
(21)

对式(21)进行实部和虚部的分离, 得

(22)

其中Re[μk(iω)]和Im[μk(iω)]分别表示μk(iω)(k=1,2)的实部和虚部, 并且

将特征方程(9)对τ求导验证横截条件：

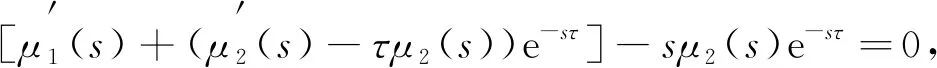
(23)

从而可得

(24)

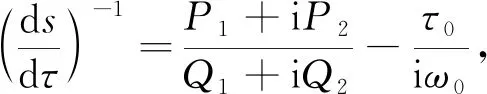
(25)

其中

因此可知

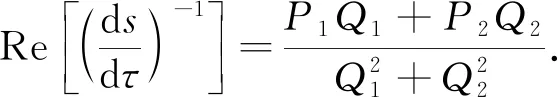
(26)

令f1(ω)=cos(ωτ),f2(ω)=sin(ωτ), 则

(27)

假设方程(27)有正实根, 结合方程(22)可得分岔阈值表达式为

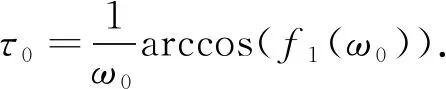
(28)

系统(3)的地方病平衡点E2在τ=τ0处发生Hopf分岔, 根据定理5及特征根关于时滞τ的连续性可知: 当τ<τ0时, 系统(3)的地方病平衡点E2渐近稳定； 当τ>τ0时, 系统(3)的地方病平衡点E2不稳定.证毕.

注2由分岔阈值τ0的表达式可知,τ0随着分数阶次αi的变化而变化, 即分数阶次的改变会影响系统的动力学行为.

4 数值模拟和仿真实验

下面利用MATLAB工具进行数值模拟和仿真实验.首先给出模型(2)的相关参数, 此时系统为

(29)

根据系统(29)计算可得R0=0.865<1, 且系统仅存在一个无病平衡点E(1,0,0).选取3组不同的时滞参数τ1=0.5,τ2=1.5,τ3=2.5, 系统分数阶次分别取α1=0.7,α2=0.99,α3=0.9.由定理4可知, 无病平衡点E1在任意时滞τ≥0下都是局部渐近稳定的, 如图2所示.

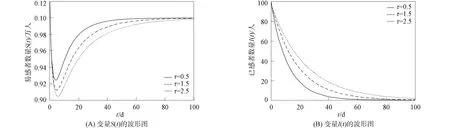
图2 系统(29)在无病平衡点E1处的全时滞渐近稳定性Fig.2 Asymptotic stability of system (29) at disease-free equilibrium point E1 with full time delay

为验证地方病平衡点E2在时滞τ=0的稳定性, 根据生态学理论重新调整参数得到系统

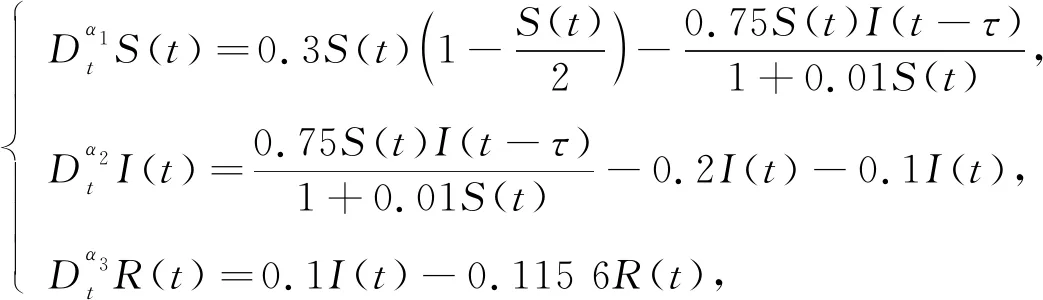
(30)

其仿真结果如图3所示.根据系统(30)计算可得R0=4.9>1, 且系统存在唯一的地方病平衡点E2=(0.401 6,0.320 9,0.277 5).显然系统(30)参数满足a+γ-a22=0.000 01>0,a11=-0.06<0.取模型分数阶次α1=0.8,α2=0.99,α3=0.9, 在时滞τ=0的情形下, 由定理5可知, 系统(30)的地方病平衡点E2是局部渐近稳定的.

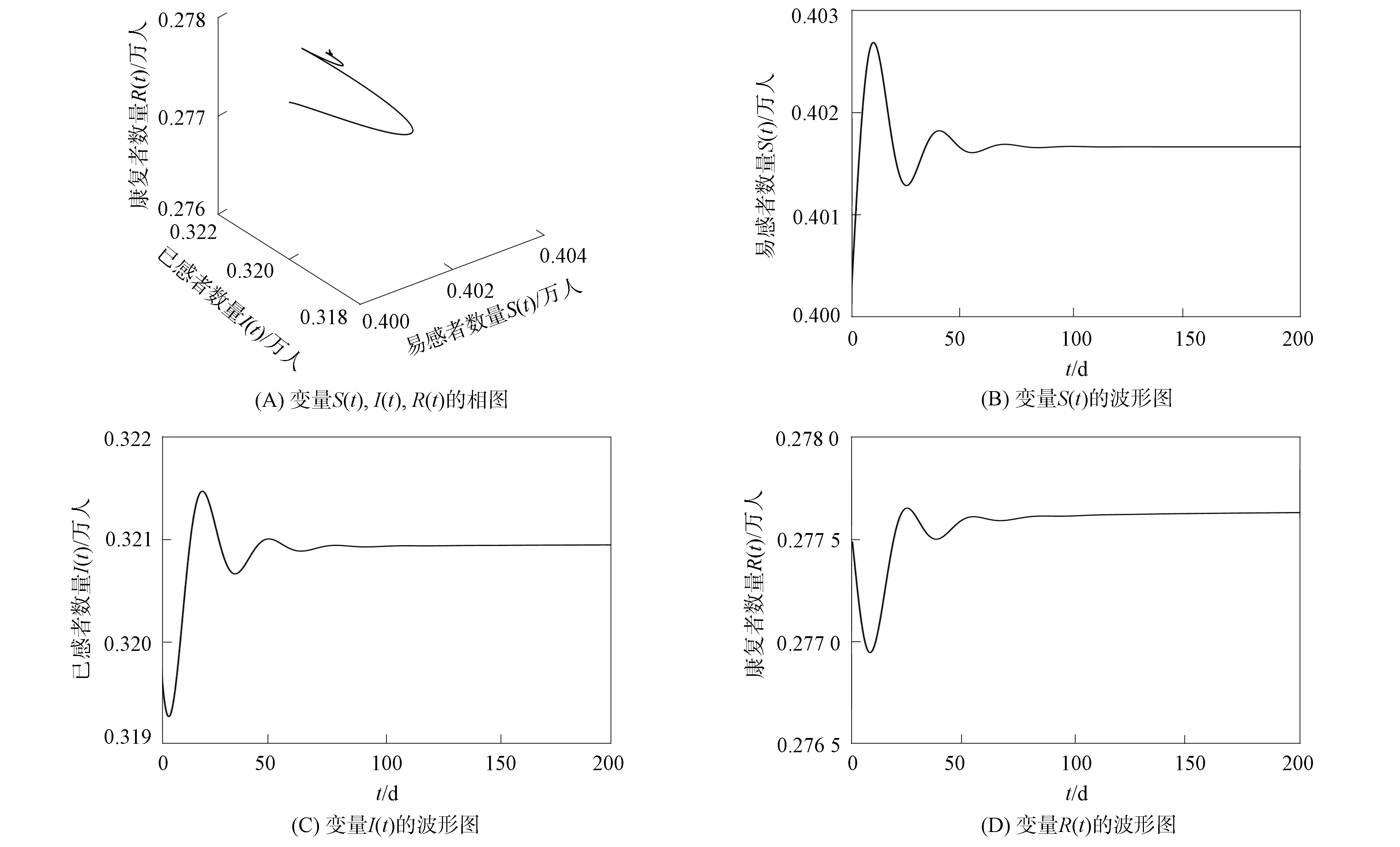
图3 当τ=0时系统(30)地方病平衡点E2的渐近稳定性Fig.3 Asymptotic stability of system (30) at endemic equilibrium point E2 when τ=0

由Hopf分岔的讨论可知, 系统(30)发生Hopf分岔的阈值τ0=5.554.选取时滞参数τ=10, 根据定理6中2)可知, 系统(30)的地方病平衡点E2不稳定, 如图4所示； 选取时滞参数τ=5, 根据定理6中1)可知, 系统(30)的地方病平衡点E2是局部渐近稳定的, 如图5所示.

图4 当τ=10时系统(30)地方病平衡点E2的不稳定性Fig.4 Instability of system (30) at endemic equilibrium point E2 when τ=10

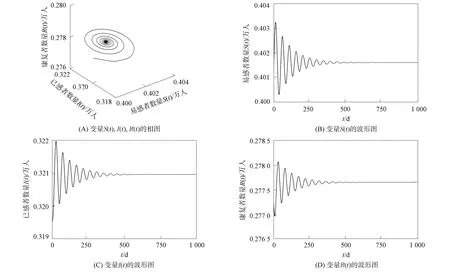
图5 当τ=5, α1=0.8时系统(30)地方病平衡点E2的渐近稳定性Fig.5 Asymptotic stability of system (30) at endemic equilibrium point E2 when τ=5, α1=0.8

为突出阶次不一致分数阶系统动力学行为的复杂性, 本文假设系统(30)的分数阶次α2=0.99,α3=0.9,τ=5.取α1=0.8, 如图5所示, 系统(30)的地方病平衡点E2是局部渐近稳定的； 但当取α1=0.9时, 如图6所示, 系统(30)的地方病平衡点E2开始不稳定了.这主要是因为改变分数阶次αi会导致系统分岔阈值发生变化.当α1=0.8时, 系统(30)的分岔阈值τ0=5.554； 当α1=0.9时, 系统(30)的分岔阈值τ0=4.129.

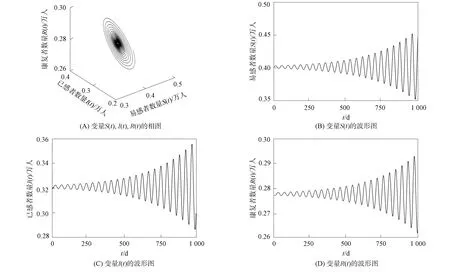
图6 当τ=5, α1=0.9时系统(30)地方病平衡点E2的不稳定性Fig.6 Instability of system (30) at endemic equilibrium point E2 when τ=5, α1=0.9

为进一步分析分数阶次对系统(30)动力学的影响, 固定分数阶次α3=0.9不变.先选择分数阶次α2=0.99, 考察分数阶次α1与系统分岔阈值τ0之间的关系； 然后选择分数阶次α1=0.9, 考察分数阶次α2与系统分岔阈值τ0之间的关系.

当α2=0.99,α3=0.9时, 由图7(A)可见, 随着分数阶次α1的增大, 分岔阈值τ0增大, 系统(30)的稳定性增强； 当α1=0.9,α3=0.9时, 由图7(B)可见, 随着分数阶次α2的增大, 分岔阈值τ0减小, 表明系统(30)的稳定性减弱.

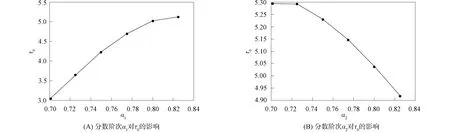
图7 分数阶次α1,α2对系统(30)分岔阈值τ0的影响Fig.7 Effects of fractional orders α1,α2 on bifurcation threshold τ0 of system (30)

综上所述, 本文首先研究了一类具有Logistic增长与饱和传染率的不同阶次分数阶SIR传染病模型. 通过公式推导得到了R0<1时系统(3)的无病平衡点E1是全时滞渐近稳定的, 给出了系统(3)地方病平衡点E2局部渐近稳定的充分条件, 并结合Hopf分岔定理给出了系统(3)产生Hopf分岔的充分条件及分岔阈值τ0的数学表达式. 其次， 采用MATLAB工具对本文研究的SIR传染病模型进行了数值仿真, 仿真结果证明了理论分析的正确性. 研究表明, 引进分数阶提高了系统的稳定性, 时滞和不同阶次分数阶使得SIR传染病模型的动力学行为更复杂, 在某些情况下随着分数阶次的改变, 系统的稳定性也随之改变.