张贵仓，拓明秀，苏金凤，孟建军,韩根亮

(1.西北师范大学数学与统计学院，甘肃 兰州 730070；2.兰州交通大学机电技术研究所，甘肃 兰州 730070；3.甘肃省传感器与传感技术重点实验室，甘肃 兰州 730030)

1 引言

Bézier和B样条方法是计算机辅助几何设计CAGD(Computer Aided Geometric Design)的2种主流方法，因具有几何不变性、保凸性等实用性质而被广泛地应用于曲线曲面设计。然而传统的Bézier和B样条曲线曲面已很难满足快速发展的几何工业的多元需求。随之，许多有理化形式的Bézier曲线被提出，但该类曲线存在渐进的问题，并且权因子使用不当容易破坏几何形状[1,2]。为解决此类问题，学者们提出了许多带有形状参数的类Bernstein基和B样条基[3 - 11]。

文献[12]将参数引入控制顶点构造出了一组带形状参数的拟Bézier曲线，并从光顺性的角度出发在能量优化的理论基础上对形状参数的取值给出了实用性建议。文献[13]在代数多项式空间中构造了一组类Bernstein基函数，其对应生成的曲线具有几何不变性和保凸性等性质。文献[14]基于文献[13]中的基函数提出了带多个形状参数的拟三次Bézier曲面。文献[15]在三角多项式空间中构造了一类带形状参数的Bernstein-Bézier曲面片。文献[16]将文献[3]中的基函数扩展到三角域上得到了三角域上带3个形状参数的基函数，并给出了形状可调性的三角域曲面。文献[17]利用奇异混合技术构造了一种简单直观的线性奇异混合样条曲线，但未全面讨论曲线的连续性及参数对曲线的影响。文献[18]将奇异混合技术加入三次λμ-α-DP曲线得到了具有几何连续性的线性奇异混合的三次λμ-α-DP曲线，但该曲线存在不能精确表示椭圆等二次曲线的缺点。

传统Bézier曲线具有单位性、对称性等优良性质，但往往不能精确表示椭圆弧等二次曲线。为了解决传统曲线出现的问题，本文将奇异混合函数和三角多项式空间中的拟三次三角Bézier基函数相结合，得到了一种带有形状参数的奇异混合拟Bézier曲线。新构造的曲线具有规范性、凸包性和几何不变性等重要性质的同时还具有灵活的形状可调性，且满足一定条件时2段奇异混合拟Bézier曲线能够达到G1及G2连续。新曲线能够克服传统的Bézier方法未能准确表示除抛物线外的圆锥曲线这一缺点。此外，基于传统的NURBS(Non-Uniform Rational B-Splines)曲线表示形式能够与传统Bézier曲线进行转化，本文方法与NURBS表示也具有较好的兼容性[19]。

2 奇异混合函数的构造

2.1 奇异混合函数的定义

定义1设f(t)是定义在函数自变量t∈[0,1]上的一个连续函数，如果f(t)满足如下条件:

f(0)=1,f(1)=0,

f(k)(0)=f(k)(1)=0,k=1,2,…,n

(1)

那么可以称f(t)是n阶奇异混合函数。

称满足式(1)且次数最小的多项式为最小奇异混合函数。

2.2 一般奇异混合函数的建立

根据定义1可知，n阶奇异混合函数至少要满足2n+2个条件，因此要求一个n阶奇异混合函数可以按照如下方法进行。

设S为某函数空间的一个子空间，并有:

S=span{φ0(t),φ1(t),…,φ2n+1(t)},

φk(t)∈Cn[0,1]

其中φ0(t),φ1(t),…,φ2n+1(t)在[0,1]线性无关，则可设奇异混合函数为:

其中，ak(0≤k≤2n+1)为式(6)中线性方程组的系数，φk(t)(0≤k≤2n+1)代表线性方程组的未知量。

由定义1可得:

(2)

(3)

(4)

(5)

若令:

φk,j=φk,k=1,2,…,2n+1;j=0,1

则由式(2)～式(5)组成的方程组可以写成如下形式:

(6)

求解式(6)就可得到所需的奇异混合函数。

3 奇异混合拟Bézier曲线的定义

文献[20]证明了当系数λ,μ∈(-2,1],t∈[0,π/2]时，基函数:

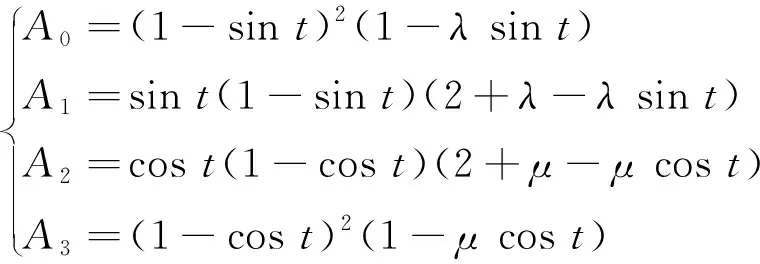
(7)

为拟三次三角多项式空间Pλ,μ=Span{1,sin2t,(1-sint)2(1-λsint),(1-cost)2(1-μcost)}中的最优规范全正基，称式(7)所给出的基函数为三次三角Bézier基函数。若令t∈[0,1]，式(7)中的基函数可以改写为:

(8)

基于该基函数对曲线曲面形状控制的有效性，利用奇异混合函数和权的思想构造出一种奇异混合拟Bézier曲线。

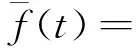
Q(t)=α(t)P(t)+(1-α(t))L(t),0≤t≤1

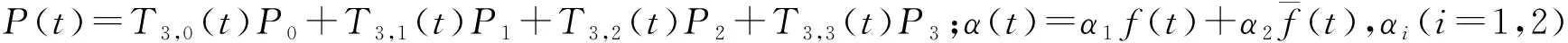
由定义2易知奇异混合拟Bézier曲线Q(t)含有4个参数α1,α2,λ,μ，通过改变它们的值就可以调节曲线的形状。为方便讨论称α1,α2为混合参数，λ,μ为形状参数。

4 奇异混合拟Bézier曲线基函数

4.1 奇异混合Bézier曲线基函数的表示

根据定义2所给的曲线表达式，可将三次奇异混合拟Bézier曲线进一步表示为:

Q(t)=α(t)P(t)+(1-α(t))L(t)=

T3,1(t)P1+T3,2(t)P2+T3,3(t)P3)+

若记

(9)

(10)

(11)

(12)

则

(13)

由式(3)知{Di(t,α1,α2,λ,μ)|i=0,1,2,3}具有权性。

引理1最小奇异混合函数在1/2处是一个不动点，即:

f(1/2)=1/2

定理1设f(t)为n(n>0)阶最小奇异混合函数，则{Di(t,α1,α2,λ,μ)|t∈[0,1],i=0,1,2,3}线性无关的充分必要条件是:

证明充分性。

设ξ0,ξ1,ξ2,ξ3为任意实数，若有:

(14)

根据最小奇异函数在端点及1/2处的性质，则有:

α1ξ0+(1-α1)ξ1=0

(15)

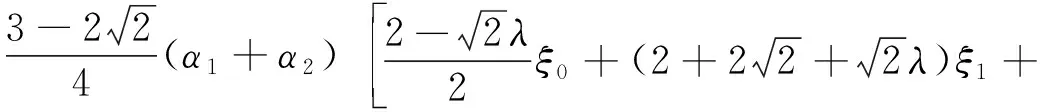
α2ξ3+(1-α2)ξ2=0

(16)

对式(14)求一阶导数，得:

根据奇异混合函数的性质及它在0与1处的导数为0，得:

(17)

(18)

必要性。

D0(t,α1,α2,λ,μ)=D1(t,α1,α2,λ,μ)=0

显然函数组{Di(t,α1,α2,λ,μ)|i=0,1,2,3}是线性相关的，因此定理得证。

□

因{Di(t,α1,α2,λ,μ)|i=0,1,2,3}具有权性及线性无关性，故可视其为一组基函数。所以，奇异混合拟Bézier曲线可以由该基表示为:

4.2 奇异混合拟Bézier基函数的性质

奇异混合拟Bézier基函数具有下列性质：

性质1规范性：

性质2非负性：对于0≤α1,α2≤1，λ,μ∈(-2,1]，则有Di(t,α1,α2,λ,μ)≥0。

性质3端点性质：

D0(0,α1,α2,λ,μ)=α1

D0(1,α1,α2,λ,μ)=0

D1(0,α1,α2,λ,μ)=1-α1

D1(1,α1,α2,λ,μ)=0

D2(0,α1,α2,λ,μ)=0

D2(1,α1,α2,λ,μ)=1-α2

D3(0,α1,α2,λ,μ)=0

D3(1,α1,α2,λ,μ)=α2

性质4对称性：

D0(t,α1,α2,λ,μ)=D3(1-t,α2,α1,μ,λ)

D1(t,α1,α2,λ,μ)=D2(1-t,α2,α1,μ,λ)

性质5退化性：若α1=α2=1，则奇异混合拟Bézier基函数退化为三次T-Bézier基函数；若α1=α2=1且λ=1,μ=1，则奇异混合拟Bézier基函数退化为三次类Bézier基函数。

4.3 奇异混合函数及参数对奇异混合拟Bézier基函数的影响

由式(9)～式(12)能够看出，奇异混合拟Bézier基函数不仅与参数α1,α2,λ,μ有关，而且与奇异混合函数也有关。下面分析奇异混合函数及参数对奇异混合拟Bézier基函数的影响。

当α1=α2=1时，奇异混合拟Bézier基函数即为式(11)所给最优规范全正基，此时奇异混合函数对奇异混合拟Bézier基函数没有影响。而由式(9)～式(12)不难发现，参数λ影响基函数D0,D1，参数μ影响基函数D2,D3，图1b和图1c分别给出了参数λ和μ的值依次增大对基函数D0,D1和基函数D2,D3的影响。当α1≠α2≠1时，参数λ和μ对基函数D0,D1,D2,D3的影响均与图1b和图1c类似，因此在下面的讨论中将视参数λ和μ为定值。

当α1=α2=0时，有：

D0(t,α1,α2,λ,μ)=D3(t,α2,α1,λ,μ)=0

此时的4个基函数是线性相关的，从某种程度上来说不能严格称之为基函数，这里不加以严格区分。图1d给出了这种情况的基函数图像。

Figure 1 Influence of parameters on singular blending quasi-Bézier basis function图1 参数对奇异混合拟Bézier基函数的影响

当α1,α2在0～1变化时，不同的奇异混合函数对基函数的影响并不明显。式(19)和式(20)是利用2.2节的方法构造的二次及五次最小多项式奇异混合函数：

f(t)=1-10t3+15t4-6t5

(19)

f(t)=(1-t)11+11t(1-t)10+

55t2(1-t)9+165t3(1-t)8+

330t4(1-t)7+462t5(1-t)6

(20)

图2给出了α1,α2取值不同的情况下最小多项式奇异混合函数对奇异混合拟Bézier基的影响，其中图2a，图2c和图2b，图2d分别代表二次及五次最小多项式奇异混合函数对基函数的影响。

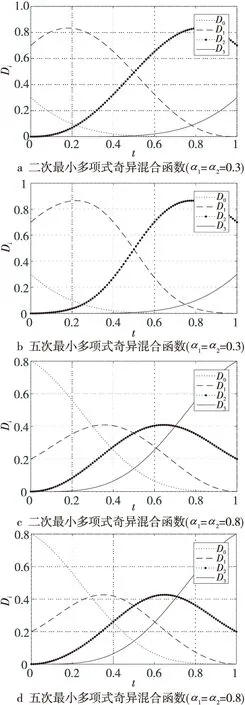
Figure 2 Influence of singular blending function on singular blending quasi-Bézier basis function图2 奇异混合函数对奇异混合拟Bézier基函数的影响

下面讨论奇异混合函数和λ,μ不变时，参数α1,α2对基函数的影响(这里采用式(19)所示的二阶最小奇异混合函数，并且λ=μ=1)。

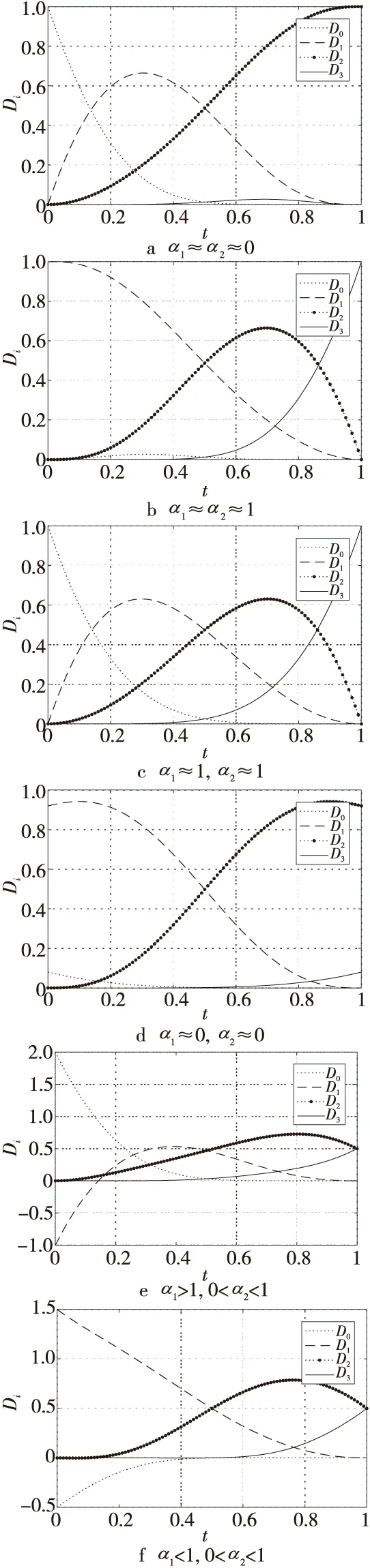
Figure 3 Influence of blending parameters α1,α2 on singular blending quasi-Bézier basis function图3 混合参数α1,α2对奇异混合拟Bézier基函数的影响

由图3a～图3d反映出当α1和α2逼近于1时，奇异混合拟Bézier基函数近似为三次三角Bézier基函数，当α1或α2向0逼近时，奇异混合拟Bézier基函数的D0或D3被严重压缩。由图3e和图3f能够看出,当α1和α2超出0～1时，奇异混合拟Bézier基函数的变化幅度较大。

5 奇异混合拟Bézier曲线的性质

根据奇异混合拟Bézier基函数的性质，可得奇异混合拟Bézier曲线具有如下性质:

性质6端点性质：

R(0)=α1P0+(1-α1)P1

R(1)=α2P3+(1-α2)P2,

(21)

性质7几何不变性和仿射不变性：由于奇异混合拟Bézier基函数具有规范性，则奇异混合拟Bézier曲线的形状只取决于控制顶点，而与坐标系的选取无关。

性质9凸包性：当α1,α2∈[0,1]时，由奇异混合拟Bézier基函数的规范性和非负性能够得到曲线具有凸包性。

性质10逼近性：α1,α2趋于0时，奇异混合拟Bézier曲线向控制多边形第2条边逼近。

性质11退化性：当α1=α2=1时，奇异混合拟Bézier曲线形式同三次T-Bézier曲线；当α1=α2=1且λ=μ=1时，奇异混合拟Bézier曲线将退化为三次类Bézier曲线。

性质12非凸包性：当α1,α2∉[0,1]时，奇异混合拟Bézier曲线超出控制顶点形成的凸包。

6 参数对奇异混合拟Bézier曲线形状的影响

6.1 形状参数λ,μ对曲线形状的影响

令α1=α2=1，在图4中λ,μ的取值增大时奇异混合拟Bézier曲线向控制顶点P1或P2趋近。λ不变μ的值越大奇异混合拟Bézier曲线越靠近控制顶点P1。μ不变λ的值越大奇异混合拟Bézier曲线向控制顶点P2趋近的程度越大。图4～图9中直角坐标系的横纵坐标表示控制顶点Pi(i=0,1,2,3)的横纵坐标。

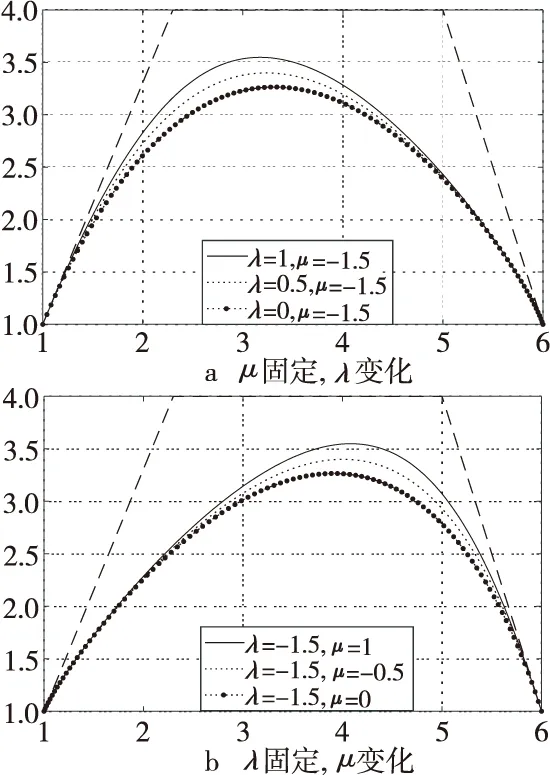
Figure 4 Influence of shape parameters λ,μ on the shape of singular blending quasi-Bézier curves图4 形状参数λ,μ对奇异混合拟Bézier曲线形状的影响

6.2 混合参数α1,α2对曲线形状的影响

为了更清楚地了解混合参数α1,α2对曲线形状的影响，令λ=μ=0.5。

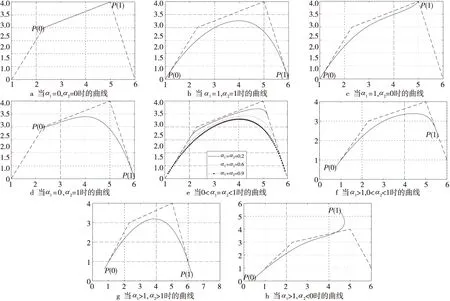
Figure 5 Influence of parameters α1,α2 on the shape of the curve图5 参数α1,α2对曲线形状的影响

如图5a～图5e所示，当参数α1和α2在[0,1]变化时，奇异混合拟Bézier曲线完全在控制多边形所形成的凸包内变化。当α1趋于1时，曲线的始点趋于P0，当α1趋于0时，曲线的始点趋于P1。因此，当参数从0变化到1时曲线的始点在P0P1上从P1变化到P0。而当参数α2从0到1变化时，曲线的终点在P2P3上从P2变化到P3。如图5f～图5h所示，由于参数α1,α2超出[0,1]，曲线被拉出控制网格的凸包。分析发现，参数α1,α2使得曲线拥有较好张力的同时具有良好的形状可调性。

7 奇异混合拟Bézier曲线曲面设计

7.1 奇异混合拟Bézier曲线的拼接

在实际造型设计过程中，单个的奇异混合拟Bézier曲线往往无法准确地描述结构复杂的曲线，为保证曲线的光滑性常采用拼接方法。

设2段奇异混合拟Bézier曲线分别为：

其中,Pi,Qi分别为2段奇异混合拟Bézier曲线的控制顶点。

经简单计算可得:

即R1(1)=R2(0)，则2段奇异混合拟Bézier曲线满足G0连续。

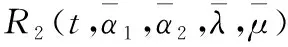
R′2(0)=ξR′1(1),ξ>0

(22)

由性质6可得:

(23)

(24)

将式(23)和式(24)代入式(22)可得：

(25)

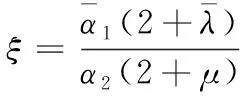
为使2段奇异混合拟Bézier曲线在公共连接点处满足G2连续，2条曲线满足G1连续的条件外还要满足：

R″2(0)=ξ2R″1(1)+δR′1(1)

由端点性质可得：

(26)

则2段奇异混合拟Bézier曲线能够达到G2连续条件为：式(25)和式(26)。图6和图7分别给出了奇异混合拟Bézier曲线的G1和G2连续的图像。

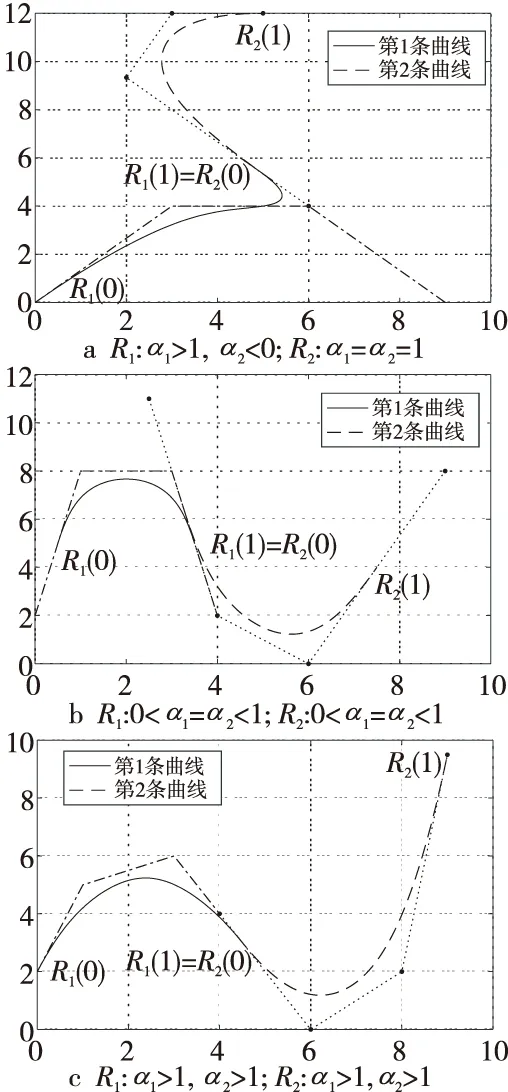
Figure 6 G1-continuous of singular blending quasi-Bézier curves图6 奇异混合拟Bézier曲线的G1连续

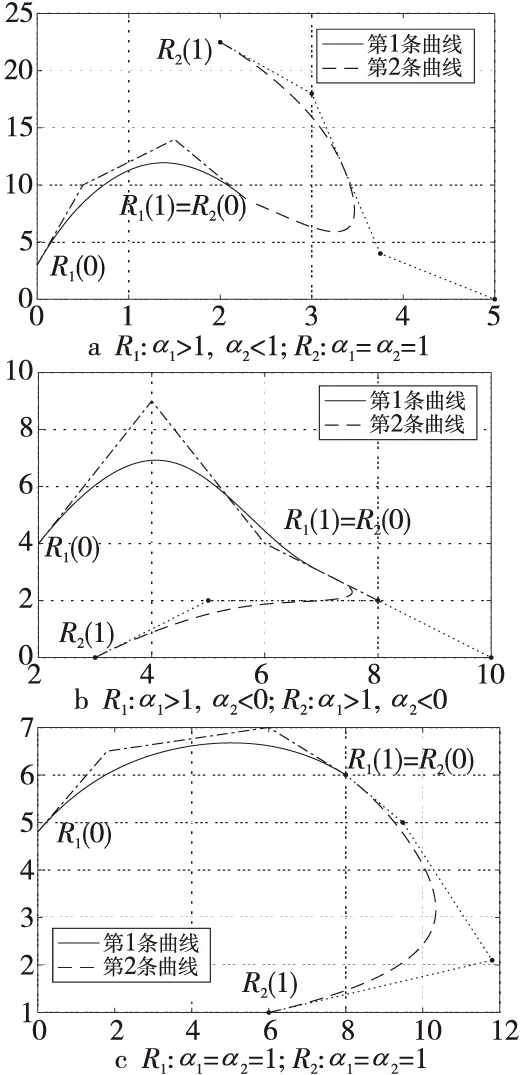
Figure 7 G2-continuous of singular blending quasi-Bézier curves图7 奇异混合拟Bézier曲线的G2连续

7.2 圆弧、椭圆弧和抛物线弧的精确表示

设控制多边形顶点为P0=(0,0),P1=(a,0),P2=P3=(2a,b)，令α1=α2=1,λ=0,μ=0，则:

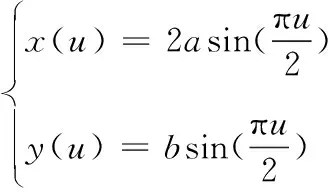
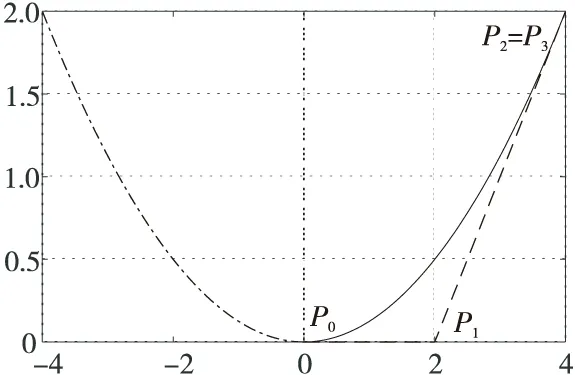
Figure 8 Accurate representation of a parabolic arc图8 抛物线弧的精确表示

设控制多边形的顶点为Q1=(0,2b),Q2=(a,2b),Q3=(2a,b),Q4=(2a,0)，令α1=1,α2=1，λ=μ=0,则有:

由此可得椭圆方程为：x2/a2+y2/b2=1,当a=b时，即为圆的方程。图9中实线部分是奇异混合拟Bézier曲线对圆弧的精确表示。

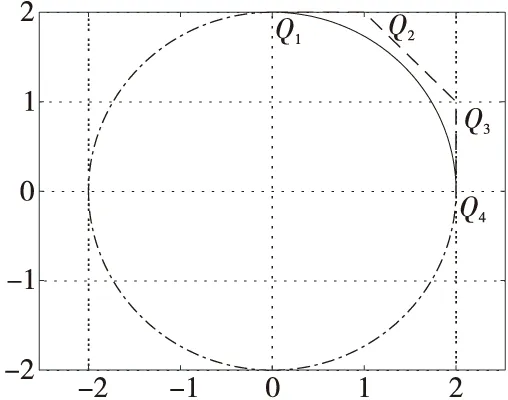
Figure 9 Accurate representation of the arc图9 圆弧的精确表示

7.3 椭球面的精确表示

用张量积的方法可以将奇异混合拟Bézier曲线推广至四边域曲面。其表达式为：

V(t,α1,α2,λ,μ,u,v)=

称为奇异混合拟Bézier曲面。

若给定合适的控制顶点及参数，则奇异混合拟Bézier曲面能够精确表示椭球面及球面。给定控制顶点:

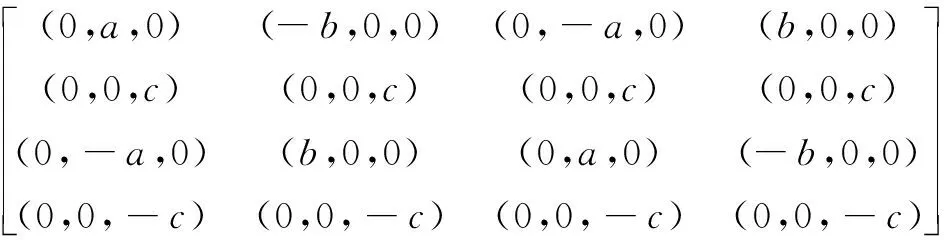
参数α1=α2=1,λ=μ=0时，可得:

当a=b=3/(2c)时表示球面，图10所示为奇异混合拟Bézier曲面表示的球面片。

Figure 10 Spherical patches represented by singular blending quasi-Bézier surfaces图10 奇异混合拟Bézier曲面表示的球面片

8 结束语

本文构造了一种带形状参数的奇异混合拟Bézier曲线，讨论了基函数及曲线的优良性质的同时详细地分析了奇异混合函数及参数对曲线的影响。本文构造的新曲线不仅有很强的形状可调性，而且还克服了传统Bézier曲线不能精确表示圆弧、椭圆弧等二次曲线的缺点。分析及实例表明，新曲线具有很强的实用性与有效性。为满足复杂曲线曲面造型设计的多元需求，还需对形状参数域曲线的光顺性的关系及曲线曲面的形状进行更深入的讨论(如尖点、拐点、重结点等)，限于篇幅将另文叙述。