何雪晴,韦煜明

(广西师范大学 数学与统计学院，广西 桂林 541000)

1 引言及预备知识

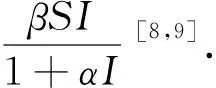
(1)

其中S(t)为t时刻的易感者数，I(t)为t时刻的染病者数，R(t)为t时刻染病者恢复数，μ为出生率和死亡率，p是成功接种者的比例(经常接种疫苗可降低易感者的出生率)，m是受感染父母的后代中易感个体的比例，n是受感染父母的后代中也患病的比例，m+n=1，γ为恢复率，λ为免疫丧失率.

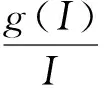
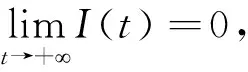
易知模型(1)的确定性模型为

(2)

2 全局正解的存在唯一性

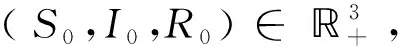
证明模型(1)中的系数是局部Lipschitz连续的，故在[0,τε)上存在唯一的局部解，τε是爆破时刻.下证τε=∞ a.s..令ε0>0使得S0>ε0,I0>ε0,R0>ε0.对任意正数ε≤ε0，定义停时τε：

τε=inf{t∈[0,τε):S(t)≤ε或I(t)≤ε},

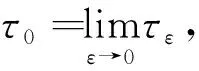
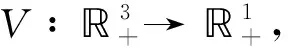
V(S(t),I(t),R(t))=-lnS(t)-lnI(t)-lnR(t).

显然V是正定的.由It公式，有

其中

于是

p+2μ+γ+λ+β+σ2∶=C,

所以

(3)

对式(3)两边从0到τε∧T积分并取期望，得到

EV(S(τε∧T),I(τε∧T),R(τε∧T))≤V(S0,I0,R0)+CT.

(4)

令Ωε={τε∧T}，对∀ε≤ε1，则P(Ωε)>δ.即，对∀ω∈Ωε，S(τε,ω),I(τε,ω),R(τε,ω)中至少有一个等于ε，所以

V(S(τε,ω),I(τε,ω),R(τε,ω))≥-lnε.

(5)

由(4)，(5)可得

V(S0,I0,R0)+CT≥E[IΩεV(S(τε∧T),I(τε∧T),R(τε∧T))]=

P(Ωε)V(S(τε),I(τε),R(τε))>-δlnε,

其中IΩε是Ωε的示性函数.令ε→0，则有

∞>V(S0,I0,R0)+CT=∞,

故τ0=∞ a.s.，引理2.1得证.

根据引理2.1，可设一个正不变集Γ，对任意初始值(S0,I0,R0)∈Γ，

由此可给出如下引理.

引理2.2 令(S(t),I(t),R(t))是模型(1)的解，(S0,I0,R0)∈Γ，则

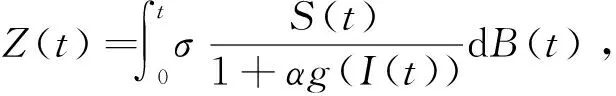
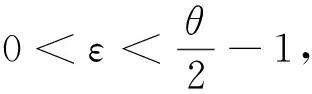
其中k为有限常数.再由Borel-Cantelli引理[13]，对几乎所有的ω∈Ω，可以得到

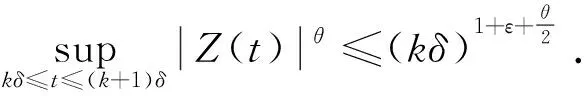
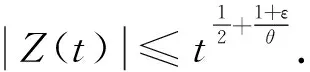
P(Ωε)≥1-ε,t≥T(ω),ω∈Ωε,

因此

故引理2.2得证.

3 疾病的灭绝性

本节给出疾病几乎必然灭绝的一个充分条件.令

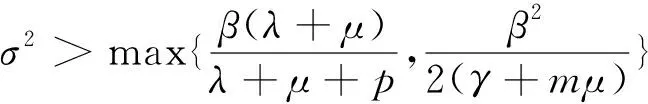
证明设(S(t),I(t),R(t))是模型(2)的解，初值(S0,I0,R0)∈Γ.对模型(2)的第二个等式利用It公式得

(6)

对式(6)两边从0到t积分，有

(nμ-γ-μ)t+M(t)+lnI(0),

(7)

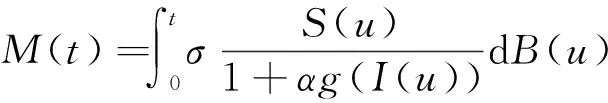
(8)

对式(8)两边同时除以t，得

(9)

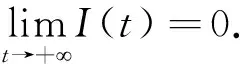
(10)

进而有

(11)

对式(11)两边同时取上极限得

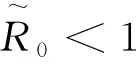
综上所述，定理3.1得证.

4 疾病的持久性

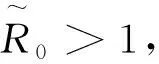
证明对模型(1)中的第三个等式的两边进行从0到t积分，并且同时除以t得到

(12)

由S(t)+I(t)+R(t)=1，可知〈S(t)〉+〈I(t)〉+〈R(t)〉=1，从而

又由(6)可知

(13)

对式(13)两端从0到t进行积分，并且同时除以t有

故

(14)

又因为R(t),I(t)≤1，故有

所以由式(12)可知

对式(14)两端同时取下极限，得到

因此定理4.1得证.

5 数值模拟与结论

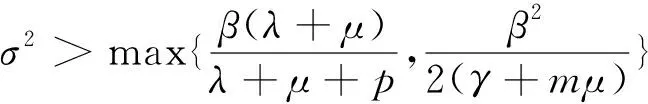
为了验证得出的结果，下面通过使用 Euler Maruyama(EM)方法[13]，对模型(1)和(2)进行数值模拟.为了验证得出的结果，取g(I)=0.001,初始值为(S0,I0,R0)=(0.7,0.5.0.3).当σ=0时，对应确定性模型(2)选取β=0.07,γ=0.113,m=0.04,n=0.96,μ=0.008,P=0.001,λ=0.002,α=0.001，则R0≈0.56<1，无病平衡点E*是全局渐近稳定的，如图1；若β=0.15，则R0≈1.60>1，地方病平衡点E*是全局渐近稳定的，如图2.

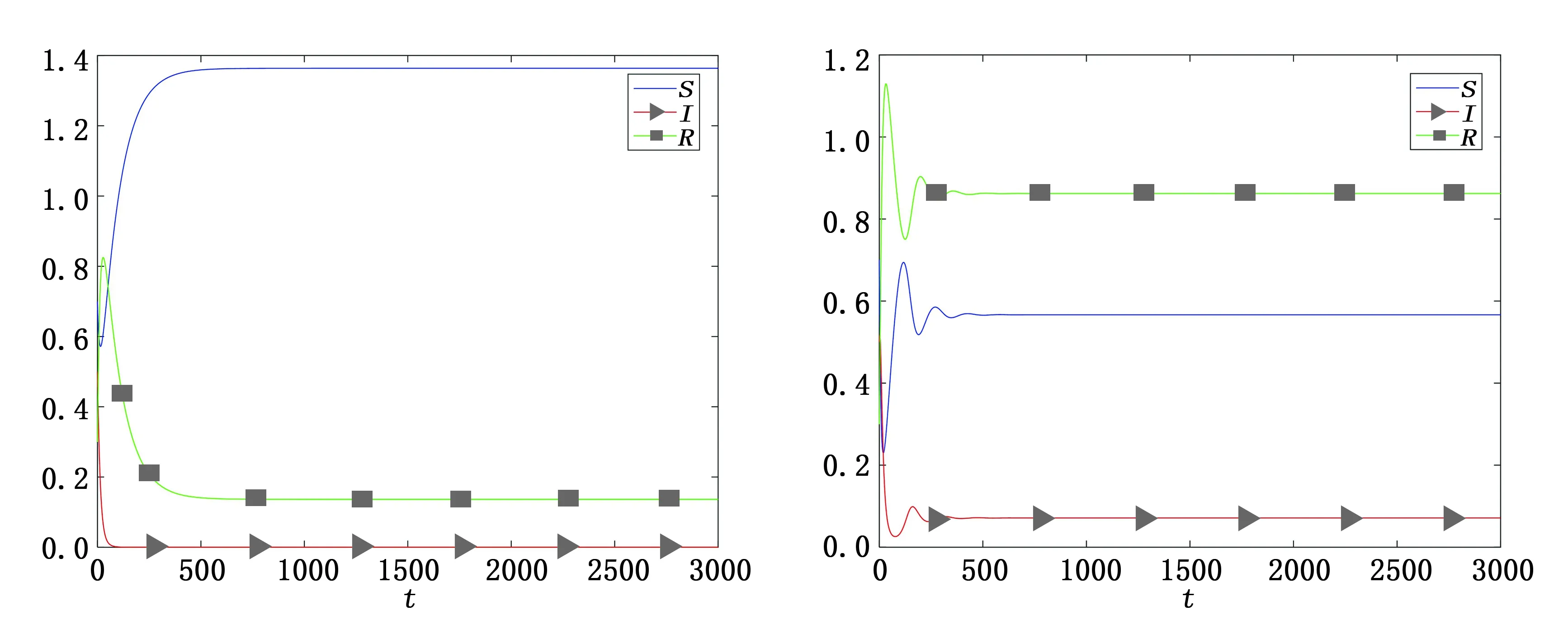
图 1 图 2

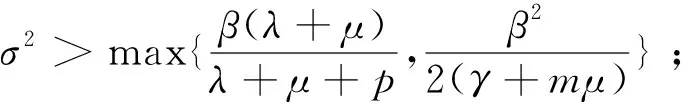
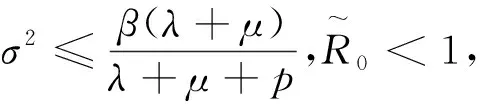
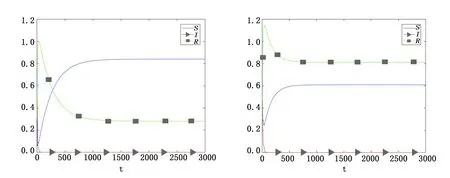
图 3 图 4

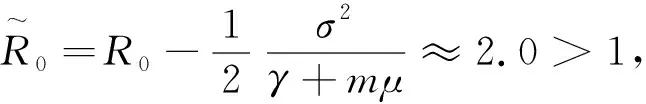
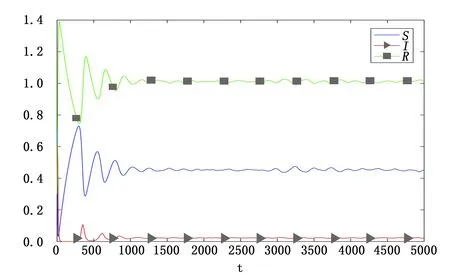
图 5