双旋弹非线性角运动特性分析
2021-04-24李佳讯沈元川贾振岳于剑桥
李佳讯,沈元川, 贾振岳,于剑桥
(1 北京理工大学,北京 100081;2 北京电子工程总体研究所,北京 100854)
0 引言
针对旋转稳定弹丸高转速的特点,通过采用鸭舵组件代替原有引信构成“双旋”结构实现对旋转稳定弹智能化、灵巧化改造已经成为该领域的强烈共识。双旋弹动力学具有强耦合、强非线性的特点,同时结构的变化与控制系统的引入使得弹丸的诸多非线性运动现象难以用线性系统理论分析和解释,因此对双旋弹开展非线性动力学分析具有重要的理论意义与工程应用价值。
双旋弹在飞行过程中有时会出现攻角大小不衰减的圆锥摆动,使得弹丸射程减小,甚至导致运动出现失稳。对于旋转弹的角运动特性分析,一般借助美国著名外弹道学者Murphy针对弹箭建立的角运动方程[1-2]。韩子鹏对弹箭的圆锥运动以及非线性角运动特性开展了深入的研究,发表了多篇学术著作[3-4]。常思江等对双旋弹前体周期性干扰引起的强迫运动进行了研究,得到了周期性舵控作用强迫项对应特解的表达式,并对前体转速闭锁问题进行了初步分析[5]。舒敬荣等研究了非线性力矩作用下气动偏心的低速旋转弹丸的强迫圆锥运动的稳定性条件[6]。
在弹道的非水平段,当偏航舵偏转到一定程度时,双旋弹角运动会产生动态失稳的现象,这种现象是双旋弹动力学分岔造成的。分岔分析是研究非线性动力学系统复杂运动行为,掌握解的拓扑结构与系统参数之间关系的一种手段,在飞行器工程领域取得了许多有价值的研究成果。Carroll等采用分岔分析方法研究了大攻角下飞行器的动力学问题[7]。许多生等提出了一种快速有效的研究方法,对飞机滚转时的惯性耦合运动进行了分岔分析和稳定性分析[8]。Gill等对标准飞行包线外的飞行器控制器特性进行了分岔分析,研究了系统稳定性与控制器参数的关系[9]。钟扬威等研究了弹箭角运动的霍普夫分岔现象,分析了飞行高度对极限环摆幅的影响[10]。
文中根据双旋弹非线性角运动方程组,从气动非线性和几何非线性两个角度分别研究了双旋弹典型的非线性运动特性。给出了基于平均法的角运动拟线性分析方法,以及基于中心流行定理的角运动分岔分析方法。结合某型双旋弹参数,得到了三次方静力矩作用下双旋弹产生稳定圆锥摆动的必要条件,同时分析了以偏航舵偏角为分岔参数的双旋弹非线性角运动分岔特性。最后通过数值仿真,验证了分析方法和结果的正确性。
1 双旋弹非线性角运动方程
对于双旋弹的角运动,可以认为双旋弹速度V、转速ωx为慢变量,故选取x=[αβωzωy]T为双旋弹非线性角运动的状态。同时假设双旋弹稳定飞行过程中α、β为小量,即sinα≈α,sinβ≈β,cosα≈1,cosβ≈1,且小量的乘积为0。进一步,忽略马格努斯力以及舵面控制力对双旋弹角运动的影响。根据双旋弹的运动方程组,可以推导非线性角运动方程为:
(1)
式中:
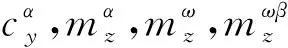
2 气动非线性下角运动特性分析
2.1 双旋弹角运动振幅平面方程
在讨论气动非线性对双旋弹角运动的影响时,可以引入水平弹道假设,即ϑ= 0°。采用Murphy稳定性理论中的复数分析方法,定义复数变量Δ=β+iα和δ=δy+iδz,从式(1)中消去ωz、ωy及其导数,可以得到双旋弹的非线性复攻角方程:
(2)
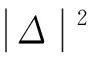
(3)
设式(3)的解具有二圆运动的形式:
Δ=K1eiφ1+K2eiφ2
(4)
定义阻尼因子λi:
(5)
将式(4)、式(5)代入式(3)得:
(6)

(7)
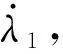
(8)
(9)
(10)
同理可以得到:
(11)
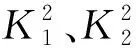
(12)
2.2 圆锥运动稳定条件
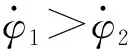
(13)
(14)
需要注意的是,λ1和λ2表达式有意义需要满足:
(15)
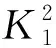
(16)
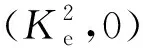
(17)
(18)
综合式(15)、式(17),由李雅普诺夫判据可知,双旋弹存在稳定的圆锥运动的必要条件为:
(19)
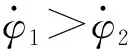
(20)
式中:

综上所述,式(19)、式(20)构成了双旋弹在三次方静力矩作用下产生稳定圆锥运动的必要条件。
2.3 仿真验证
为验证上述结论的合理性,选取不同气动参数组合进行数值仿真,如表1所示。

表1 气动参数表
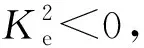
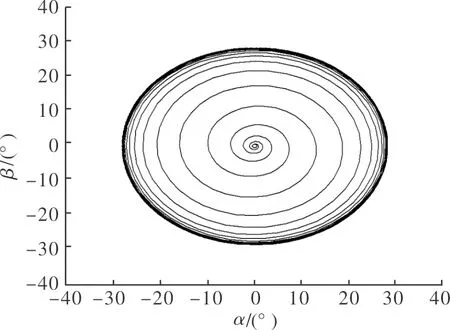
图1 算例1中初始状态在极限环内的相轨
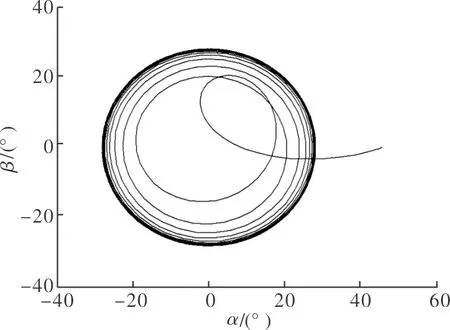
图2 算例1中初始状态在极限环外的相轨
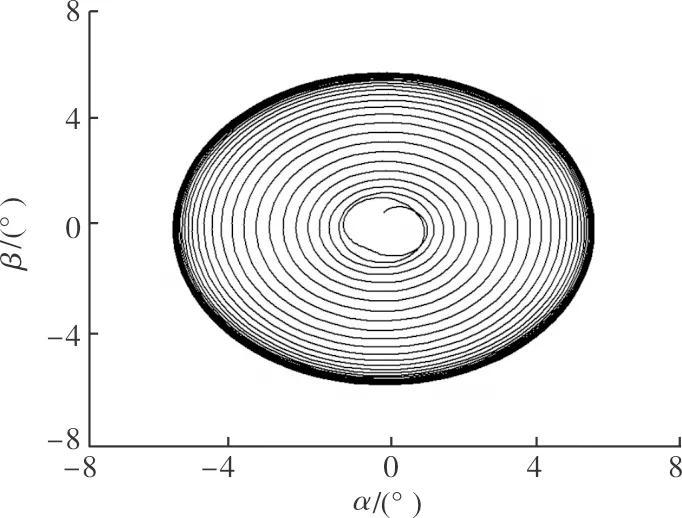
图3 算例2中初始状态在极限环内的相轨
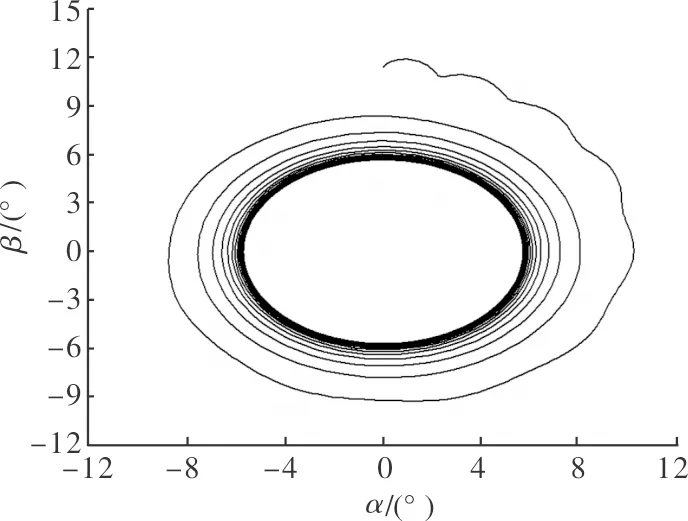
图4 算例2中初始状态在极限环外的相轨
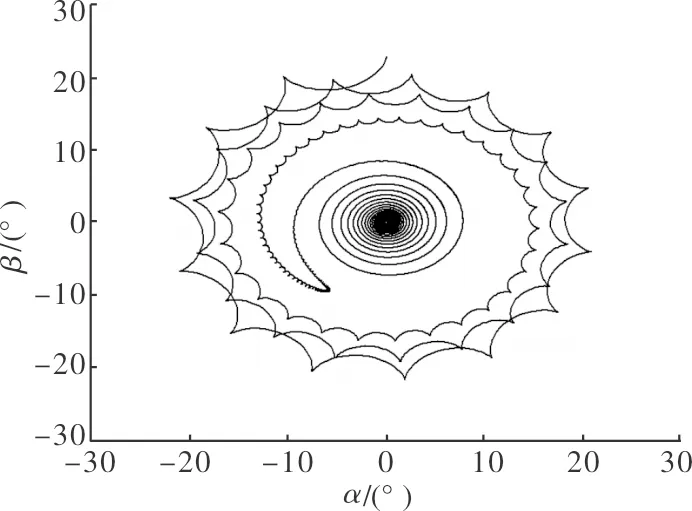
图5 算例3中相轨
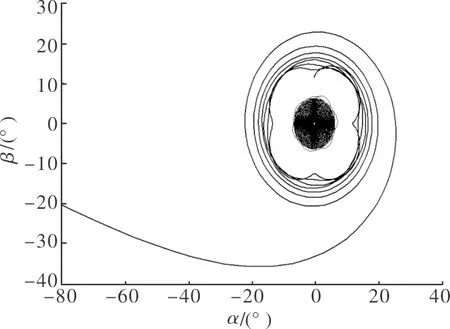
图6 算例4中相轨
3 几何非线性下角运动特性分析
3.1 角运动稳定边界条件
设γ=[δyδz]T是含参非线性系统式(1)的参变量,设系统的平衡状态为xe(γ)=[αeβeωzeωye]T,则系统在平衡状态的雅克比矩阵为:
(21)
对应的四阶特征方程可以表示为:
s4+p1s3+p2s2+p3s+p4=0
(22)
对于稳定飞行的双旋弹,ωze、ωye的数值非常小,取ωze≈0,ωye≈0,并做mΔ≈M,mω≈PT的近似处理,则式(22)中特征方程系数表达式为:
(23)
若忽略αe,并令HPT-PM=Q,根据四阶劳斯-霍尔维茨判据,系统在平衡状态稳定的充要条件为特征方程式(22)的系数满足如下条件:
(24)
将式(23)代入式(24)可以得到关于βetanϑ的二次不等式:
r1(βetanϑ)2+r2(βetanϑ)+r3<0
(25)
其中多项式系数满足:
(26)
对于双旋弹一般有M>>HT,则可由式(25)得到系统稳定时βetanϑ需要满足的边界条件为:
β1<βetanϑ<β2
(27)
式中:
由式(27)可以得到系统稳定时δy需要满足的边界条件为:
(28)
式中:
3.2 分岔特性分析
在临界点处,系统平衡状态稳定性发生了突变,其动力学发生了分岔现象,下面对双旋弹的分岔性态进行计算分析。
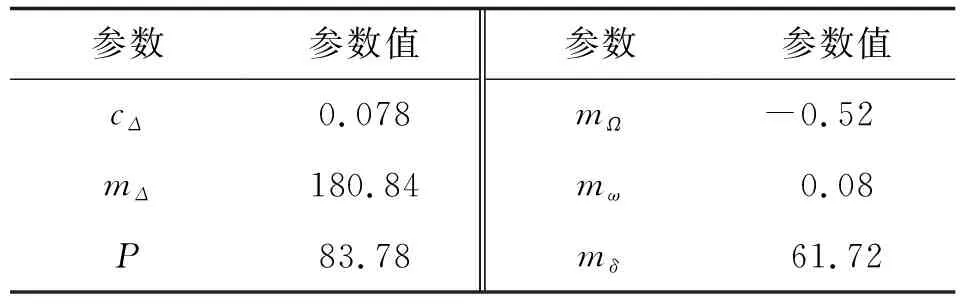
表2 气动参数表
考虑ϑ=-45°,以δy为分岔参数μ,使用x1,x2,x3,x4表示系统的状态,将表2的气动参数代入角运动方程式(1)中,得到含参非线性系统:
(29)
使用式(28)的结论,可以验证当μ=μ0=0.2时,系统稳定性发生突变,此时系统的平衡点与雅克比矩阵特征值如表3所示。在此平衡点处,特征值为两对共轭复数,一对特征值具有负实部,另一对特征值实部为零。根据霍普夫分岔定理[11],该平衡点为系统的一个霍普夫分岔点,且系统在分岔点附近将会产生极限环。下面将对系统在分岔点附近的运动特性进行深入分析。
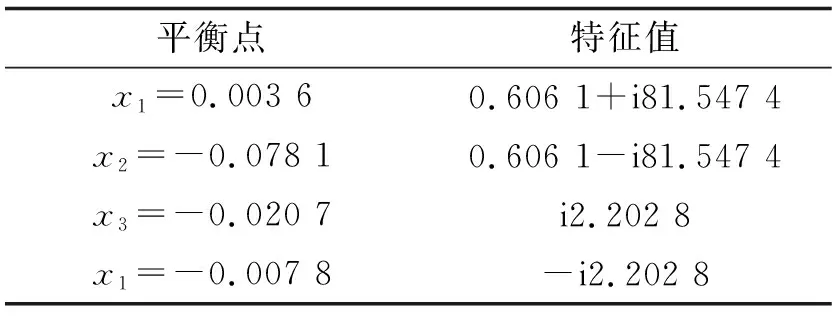
表3 系统平衡点和雅克比矩阵特征值
不失一般性,在分岔点附近将平衡点拟合为分岔参数μ的线性函数,将系统的原点移至平衡点,并令μ=λ+μ0,则双旋弹角运动方程在分岔点附近可以等价描述为:
(30)
根据文献[12]中心流行定理的计算方法,取非奇异线性变换矩阵B为表3每对共轭特征值所对应的一个特征向量的实部与虚部构成的方阵,如式(31)所示。

(31)
做非奇异变换x=By,系统式(30)可以变换为:
(32)
其中G(y,λ)为系统的非线性项。根据中心流行定理,系统式(32)过霍普夫分岔点(0, 0)有二维稳定流行和中心流行,可以计算出二维中心流行为:
(33)
其中H.O.T表示3阶以上的高阶项。
将式(33)代入式(32)中可以得到原系统降维后的二维约化方程:
(34)
根据中心流行定理,原系统在霍普夫分岔点附近的运动特性可通过分析约化方程式(34)来确定。
令y1=rcosθ,y2=rsinθ,将约化方程式(34)在极坐标下写成规范形形式:
(35)
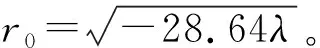
3.3 仿真验证
为了验证上述结论的有效性,将式(27)、式(28)计算结果与Matcont数值仿真结果进行对比。当ϑ=45°时,由式(27)、式(28)可以得到双旋弹角运动稳定时βe所需要满足的边界条件为-26.6°<βe< 2.3°,对应的,δy所需要满足的边界条件为-8.5°<δy< 76.4°;当ϑ=-45°时,由式(27)、式(28)可以得到双旋弹角运动稳定时βe所需要满足的边界条件为-4.5°<βe< 26.5°,对应的,δy所需要满足的边界条件为-79.5°<δy< 11.5°。
Matcont数值仿真结果如图7、图8所示。图7为ϑ= 45°时,平衡攻角、侧滑角随δy变化的曲线,l1,k1段对应的为不稳定的平衡攻角、侧滑角,l2,k2段对应的为稳定的平衡攻角、侧滑角,当δy=-8.8°时系统的平衡状态属性发生了突变,对应图中H1点,此时αe=-0.07°,βe=2.4°;图8为ϑ=-45°时的分岔图,l3,k3段对应的为稳定的平衡攻角、侧滑角,l4,k4段对应的为不稳定的平衡攻角、侧滑角,当δy=13.5°时系统的平衡状态属性发生了突变,对应图中H2点,此时αe=0.2°,βe=-4.9°。数值仿真得到系统失稳边界的βe,δy与式(27)和式(28)计算得到的稳定边界基本一致,表明稳定边界条件可以作为偏航舵偏角引起双旋弹在非水平弹道处动态失稳的判定依据。
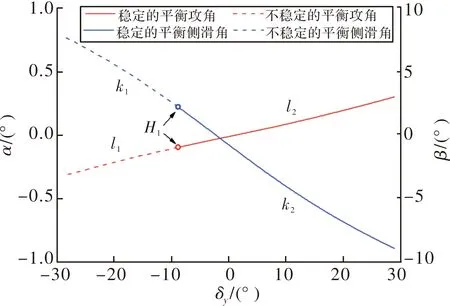
图7 ϑ=45°时以δy为分岔参数的分岔图

图8 ϑ=-45°时以δy为分岔参数的分岔图
为验证式(35)描述的系统在分岔点附近的运动特性,使用Matcont对系统的分岔现象进行了数值仿真计算,系统平衡状态αe,βe随分岔参数δy的变化如图9所示。随着δy的变化,系统在δy,0处产生了霍普夫分岔,系统的平衡状态由稳定的平衡点突变为不稳定的平衡点,并在稳定平衡点一侧产生不稳定极限环,极限环的幅值随着|δy-δy,0|增大而增大。数值仿真结果与理论分析结论一致,表明上述分岔分析方法能够准确描述双旋弹的角运动特性。
4 结论
根据双旋弹的非线性角运动方程,从气动非线性和几何非线性两个方面对双旋弹非线性运动特性进行了分析,结论为:
1)三次方非线性静力矩作用下的双旋弹,在满足式(19)、式(20)所确定的约束条件时,其角运动能够产生稳定的圆锥运动,此时双旋弹攻角不衰减,会影响弹丸的射程,甚至导致飞行失稳,对于双旋弹的结构、气动设计具有指导意义。
2)当双旋弹的弹道不平直时,且当偏航舵偏角增大到一定程度时,产生的头部侧向控制力会导致角运动动态失稳。在临界点处动力学发生了霍普夫分岔现象,越过分岔点稳定的平衡状态消失,而在稳定分岔点一侧产生了不稳定的极限环。控制方案的设计过程应避免使双旋弹角运动进入不稳定极限环与不稳定平衡点的吸引域。
