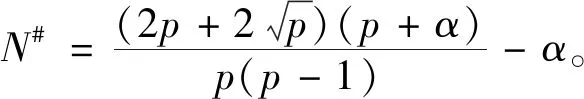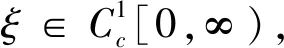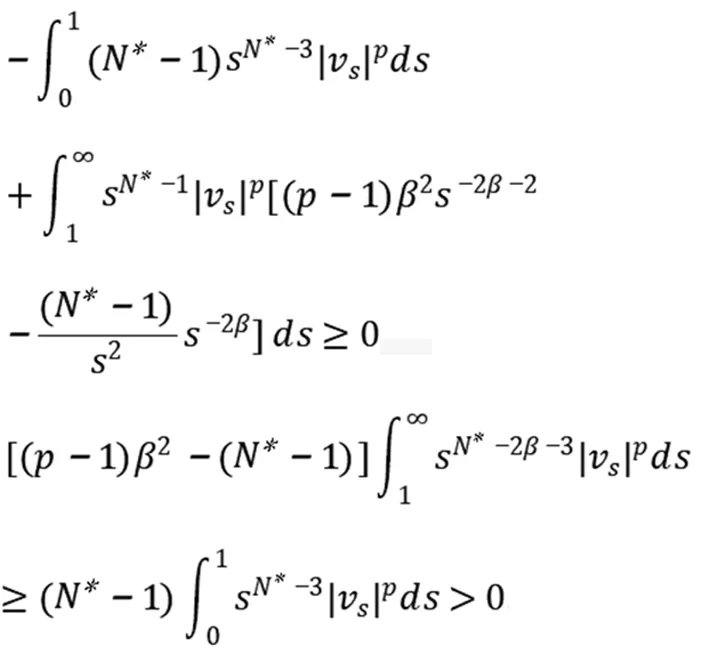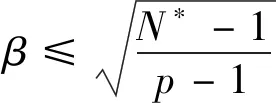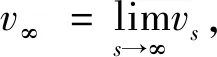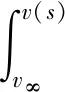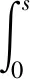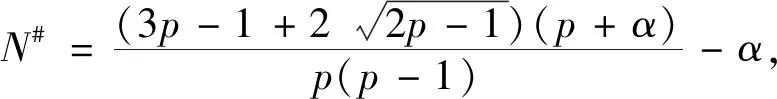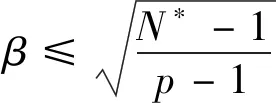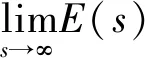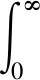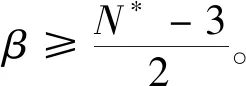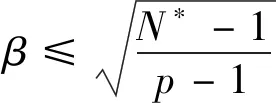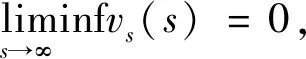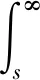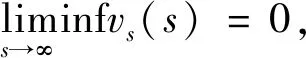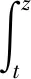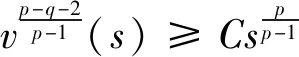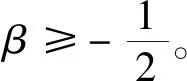加权p-Laplace方程径向解的低维不稳定性
2021-04-21张丹蕾
张丹蕾
(广西师范大学 数学与统计学院,广西 桂林 541006)
0 引言
本文主要研究以下方程
-Δpu(x)=|x|αf(u(x))x∈RN
(1)
其中Δpu(x)=div(|▽u|p-2▽u),f∈C1[a1,a2],-∞≤a1

成立,则称u为方程(1)的弱解。
定义2 设u为方程(1)的弱解,若对任意
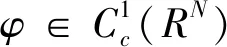
成立,则称方程(1)的弱解u为稳定的。
若u为方程(1)的稳定弱解,由(▽u▽φ)2≤|▽u|2|▽φ|2有
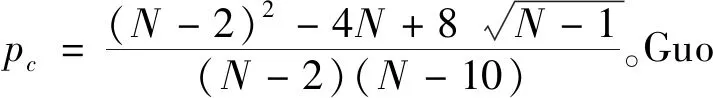
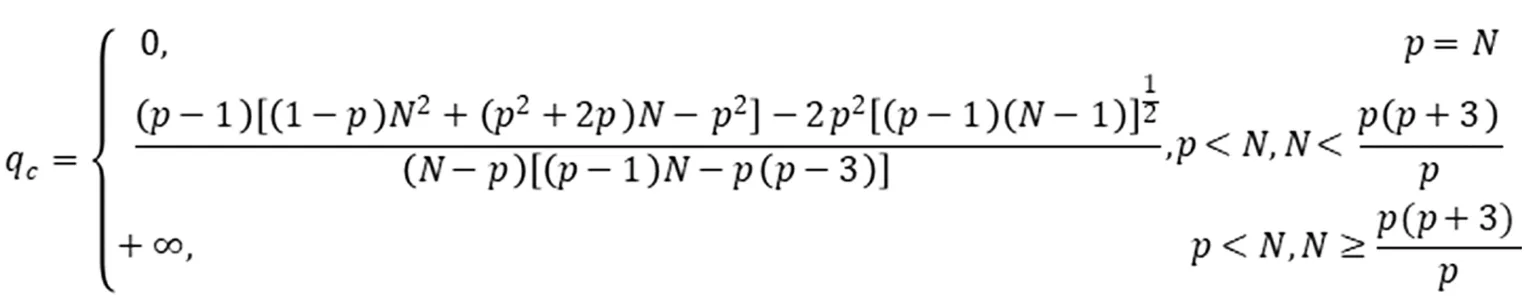

本文主要研究幂权重|x|α对p-Laplace方程径向解稳定性的影响。目标是在p≥2,α+p>0且允许存在单侧有界解u的情况下,寻找临界维数N#,使方程(1)的任意非常数径向解在p≤N≤N#时均为不稳定的。
为了避免符号混乱,用u(r)代替u(x),其中r=|x|,x∈RN。用ur表示径向函数u的径向导数。
1 记号与引理
若u为定义在G上的函数,记

χ(0,S)={1,x∈(0,S)
0,x∉(0,S)


关于方程(1)的径向解有一个有趣的事实,即通过变量的适当变换,含有幂权重|x|α的方程(1)可以在新的分数维中转化为具有常数权重的p-Laplace方程。为此,参考p=2时Cowan-Goussonb给出的具体方法[8],并将它推广应用到RN中。



直接计算,有
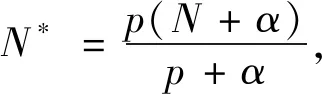
又由Δp,Nu(r)=-rαf(u(r)),有

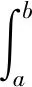
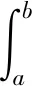
(2)
且vs在[a,b]中不改变符号。
证明由v(s)为
的稳定径向弱解,我们有vs(0)=0,且对任意
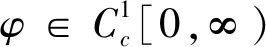
(3)
(4)
由经典椭圆正则性理论[9]知vs∈C2[a,b],0 (5) 用sN*-1ψs,ψ∈C1[a,b]乘以(5)式且在(a,b)上分部积分 +(sN*-1|vs|p-2vs)s]ψds 因此, 下证vs在[a,b]中不改变符号。 给定s0>0使vs(s0)≠0,由vs的连续性可令(a0,b0)为[0,+∞)中vs≠0的最大区间,其中0≤a0 反证,假设b0<+∞,对很小的ε>0,在(a0+ε,b0-ε)上应用(2)式,且令ψ=vs有 (6) 由(5)式与洛必达法则得,a0=0时,有 a0>0时,有 综上可得 (7) 因此,有 sN*-3|vs|p∈L1(a0,b0) (8) 在(6)式中令ε→0,由vs(a0)=vs(b0)=0,得 (9) 由(8)式,有 (10) 给定ε>0,令0≤φ≤1在R中满足 由φ定义我们有 由(7)式与推广的积分第一中值定理,存在η∈(a0+ε,a0+2ε)有 (11) 由Holder不等式、(10)式和(11)式,有 由(9)式与上述不等式,有 矛盾。所以vs在[a,b]中不改变符号。 证明由上述引理,若v(s)为 的稳定径向弱解,不妨设(0,∞)中有vs<0。由经典椭圆正则性理论,可以找到v∈C3(0,∞)为(5)式在(0,∞)中的解。由(8)式得 (12) 令ε→0+,有 (13) 由(12)式,有 令(4)式中φ=ξvs,由(13)式有 ≥0 (14) 现在,对β>0选择 ξ={1,s<1, s-β,s≥1 将(ξ-S-β)χ(0,S)应用于(14)式且令S→∞,有 假若有 (15) E(s) 由f∈L1(a1,a2)有E∈C1(0,∞)。直接对E(s)微分且由(5)式,有 E′(s) 即有 由f∈L1(a1,a2)有 证明若v(s)为 由E′(s)<0知,当s>0时,E(s)≤E(0)。因此,由上式知,对任意的s>0有0≤E(s)≤E(0),即E为有界的。由假设f∈L1(a1,a2)知F(v(s))也为有界的。由E(s)定义有vs∈L∞(0,∞),那么,有 证明若v(s)为 不失一般性,假设在(0,∞)中有v∞=0,v>0,vs<0。由v∈C3(0,∞)可直接对(5)式微分,有 即有 (16) 由(5)式与洛必达法则,有 当f(0)>0时,对某些δ>0,s→+∞时有|vs|p-1≥δs→+∞;当f(0)<0时,对某些δ>0,s→+∞时有|vs|p-1≤-δs→-∞。因此,有f(0)=0。下证f′(0)≤0。 若f′(0)>0,那么对很大的s与某些ε>0,有f′(v(s))≥ε>0。对满足 的截断函数φ,由 得 由vs∈L∞(0,∞),对很大的R有εRN*≤CRN*-2,与R很大矛盾。所以f′(0)≤0。 由假设我们有 (17) 由(16)式,对很大的s有(sN*-1|vs|p-2vss)′≤0。因此,对很大的s有sN*-1|vs|p-2vss非增,即对很大的s有|vs|p-2vss≤Cs1-N*。 N*>2时,上述不等式在(s,∞)上积分,有 即对任意很大的s有 (18) N*=2时,由vs∈L∞(0,∞),(18)式显然成立。 b>0时,由f(0)=0,f′(0)≤0,有q>0。因此,由(17)式,对某些δ>0和任意小的t>0有f(t)≥δtq+1。由(5)式,对很大的s有 上述不等式在(t,z)上积分,其中t很大且t -zN*-1|vs(z)|p-2vs(z) -tN*-1|vs(t)|p-2vs(t) (19) 由假设vs<0知,当s 代入(19)式,有 -|vs(z)|p-2vs(z)v-(q+1)(z) 即对2t (20) 下证q≥p-2。反证,若q 其中C>0,D>0为常数,即对很大的s有 vq+2-p(s)≤Cs-p (21) 由(17)式知,对任意的t∈[0,v(0)]有f(t)≤C′tq+1。因此,由(5)式与(21)式可得,对任意的s>0与某些C>0有 -(sN*-1|vs|p-2vs)′≤C′sN*-1vq+1 ≤{C, 0≤s<1 CsN*-1-pvp-1,s≥1 N*=p时,由vs<0有 =vp-1(0)lnz N*>p时,由vs<0有 综上所述,z>1时有 zN*-1|vs(z)|p-1 C+Cvp-1(0)lnz,N*=p 因此,对足够大的s有 |vs(s)|≤{s-1,N*>p (22) 由(18)式与(21)式我们讨论两种情况: p≤N* 当N*≥p+1时,由s≥1时有|vs(s)|≤Cs-1成立,与vs∈L∞(0,∞)有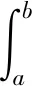
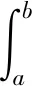
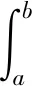
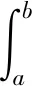

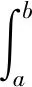
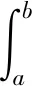
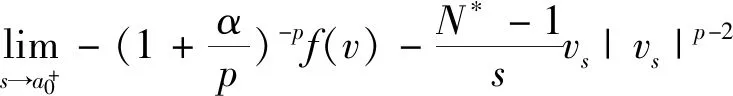

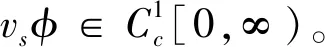
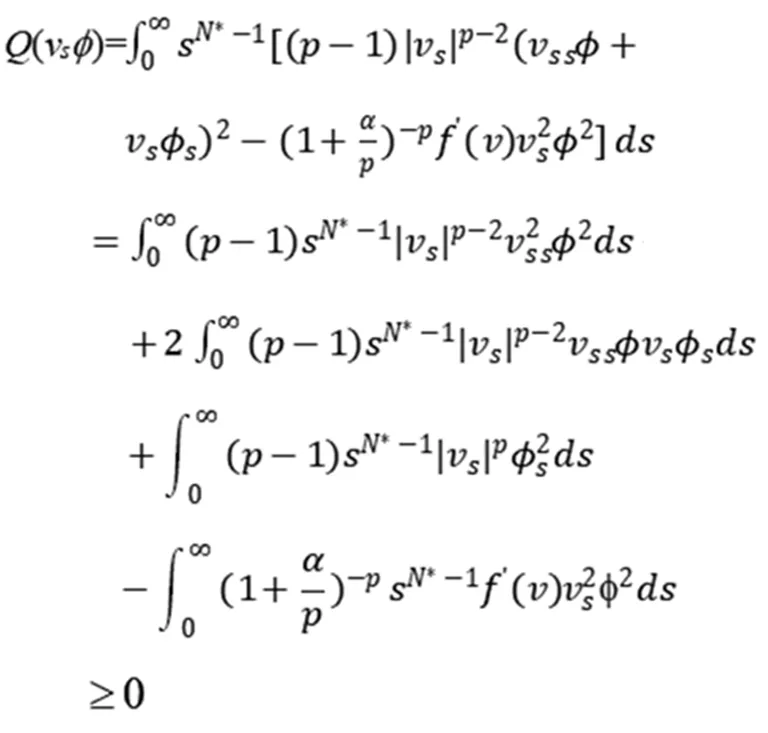


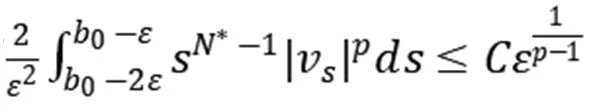
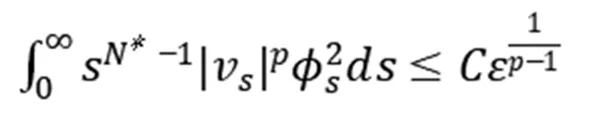


2 主要结果