段 萍, 王 旭, 丁承君, 冯玉伯, 秦 越

(河北工业大学 机械工程学院,天津 300130)

0 引 言

由于滚动轴承振动信号是非线性、非平稳信号,使得以傅里叶变换为基础的传统方法难以取得较好效果[1]。经验模态分解(empirical mode decomposition,EMD)是一种自适应的信号处理方法,适用于非线性、非平稳信号的分析,但该方法存在模态混叠和端点效应等缺点[2]。对此,Gilles J[3]提出了经验小波变换(empirical wavelet transform,EWT),能够有效避免模态混叠和端点效应的产生。文献[4]成功将EWT运用到机械故障诊断中,并与EMD进行对比,结果表明EWT分解效果优于EMD方法。奇异值熵在机械信号信息成分分析和信息量评估等方面具有独特性能,其原理是利用延时嵌陷技术对时间序列进行相空间重构。文献[5]将EMD和奇异值熵相结合运用到转子系统诊断中；文献[6]提出了一种基于EEMD和奇异值熵的滚动轴承故障诊断方法。以上方法都是对信号整体进行描述,并没有对分解后的固有模态分量(intrinsic mode function,IMF)进行局部描述。

常用的特征提取方法获取的故障信息一般是高维的,为故障分类带来很大难度[7]。因此,有必要利用降维算法对高维特征进行处理,以减少分类器的复杂度和计算量。传统的线性降维方法如主成分分析(principal component analysis,PCA)虽然对线性数据具有良好效果,但实际中高位数据都具有非线性特征,采用传统方法很难精准反映出数据之间的相关性[8]。t分布随机领域嵌入(t distributed stochastic neighbor embedding,t-SNE)是目前非线性降维算法中较为流行的方法,具有优异的降维能力和良好的可视化效果[9]。

基于以上分析,本文求取IMF的奇异值熵,来评估信号局部特征。将经验小波变换、奇异值熵和t-SNE相结合并应用到滚动轴承故障识别中,通过实验验证所提方法的有效性。

1 基础理论

1.1 经验小波变换

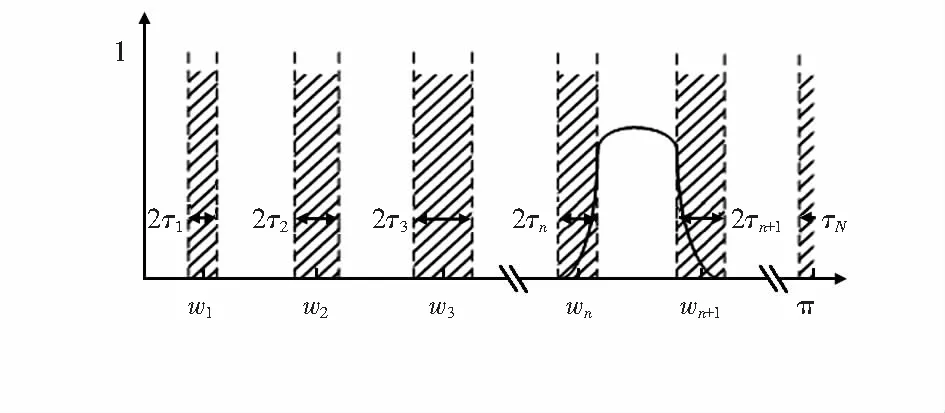
图1 傅里叶轴的分割

在确定Λn区间后,经验小波定义为Λn上的带通滤波器,借用Meyer的小波构造思想,得到经验尺度函数n(w)和n(w)经验小波函数分别为

(1)

(2)

式中γ为伸缩因子；β=x4(35-84x+70x2-20x3)；γ<(wn+1-wn)/(wn+1+wn)。

傅里叶谱的分割至关重要,这将影响信号分解的结果。将傅里叶谱分割成N段,去掉0和π以后还有N-1个边界需要确定。本文选取局部极大值方法,用于检测轴承频谱中的局部极大值并按降序排序。找到前N-1个极大值来确定相关段数,将边界wn定义为两个连续最大值之间的中心。

原始信号f(t)的重构公式如下

(3)

f0(t)=Wf(0,t)*φ1(t),fk(t)=Wf(k,t)*ψk(t)

(4)

1.2 奇异值熵

奇异值是矩阵的固有特征,当滚动轴承的状态发生变化时,对应的奇异值也随之改变。为了更好地描述滚动轴承运行状态,引入奇异值熵的概念对振动信号进行描述。奇异值熵的定义如下：

1)任何矩阵H的奇异值分解为

H=USVT

(5)

式中U和V为正交矩阵；S为矩阵H的奇异值矩阵,S=diag(σ1,σ2…,σn)。

3)根据信息熵的定义来构造奇异值熵,计算

(6)

1.3 t分布随机领域嵌入

t分布随机邻域嵌入能够有效地将高维数据的内部关系以可视化的方式表示出来[7]。t-SNE算法核心思想是以条件概率形式来表示样本的相似度并假设高维空间符合高斯分布,采用t分布计算低维空间中样本点的相似度。t-SNE算法步骤如下

1)计算高维空间中任意两个数据点xi和xj之间的条件概率密度pj|i

(7)

式中σi为数据点xi的高斯分布方差。

2)计算高维样本的联合概率密度pij

pij=(pj|i+pi|j)/2n

(8)

3)初始化低维空间的样本数据Z(0)={z1,z2,…,zn}。

4)利用自由度为1的t分布计算低维空间样本点的联合概率密度fij和梯度∂C/∂zi

(9)

(10)

式中C为KL距离定义的代价函数。

5)根据式(11)得到低维数据

(11)

式中α为学习率；h为迭代次数；动量m(h)为优化参数；∂C/∂Z为目标函数梯度。

6)迭代循环步骤(4)、步骤(5),直到迭代次数满足。

2 IMF奇异值熵和t-SNE的故障识别

2.1 定义IMF奇异值熵

IMF奇异值熵的定义如下：

1) 设长度为N的原始信号x(t)在进行EWT分解后得到n个IMF,利用延时嵌陷技术对IMF分量进行相空间重构,设相空间长度为M,则得到阶数为M×(N-M+1)的Hankel矩阵A,即

(12)

2) 将A代入式(5)进行奇异值分解得到矩阵的奇异值S=diag(σ1,σ2,…,σM),并对各个奇异值进行归一化处理。

3) 将上述的结果代入式(6),可以得到原始信号x(t)的IMF奇异值熵P。

2.2 故障识别方法设计

在本文研究中,基于IMF奇异值熵和t-SNE的滚动轴承故障识别方法如图2所示。

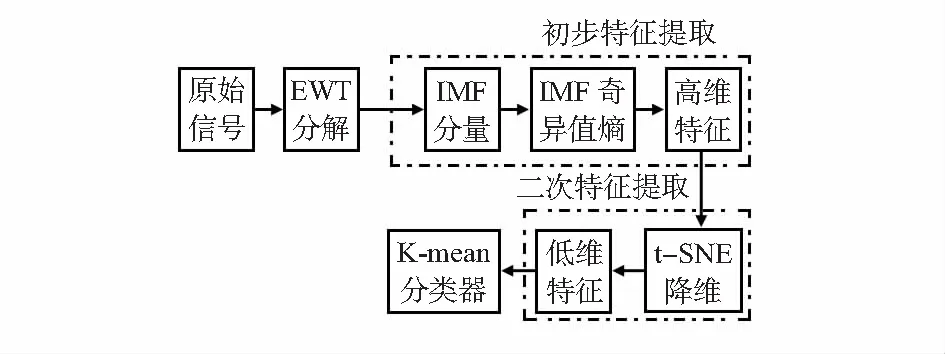
图2 故障识别流程图

3 实验与结果分析

3.1 实验数据采集

本文以美国凯斯西楚大学的实验平台作为研究对象,以验证方法的有效性。该平台由扭矩传感器、两马力电动机、测力计和电子控制设备组成。轴承型号是6205—2RS深沟球轴承,电机功率1 494 W,转速1 730 r/min,故障是利用电火花技术在外圈、内圈和滚动体上加工0.533 mm×0.279 mm的凹坑来模拟。

设置采样频率为12 kHz,采集正常、内圈故障、滚动体故障和外圈故障四种状态振动信号各40组,采样点数为2 048,滚动轴承的四种状态的振动信号如图3所示。

图3 原始振动信号时域波形图

3.2 特征提取与故障识别

1)特征提取分析

随机选取滚动轴承内圈故障信号进行分析。EWT分解的结果主要由尺度函数和傅里叶谱的分割段数N决定,本文取N=7。如图4所示为内圈故障信号EWT分解结果。

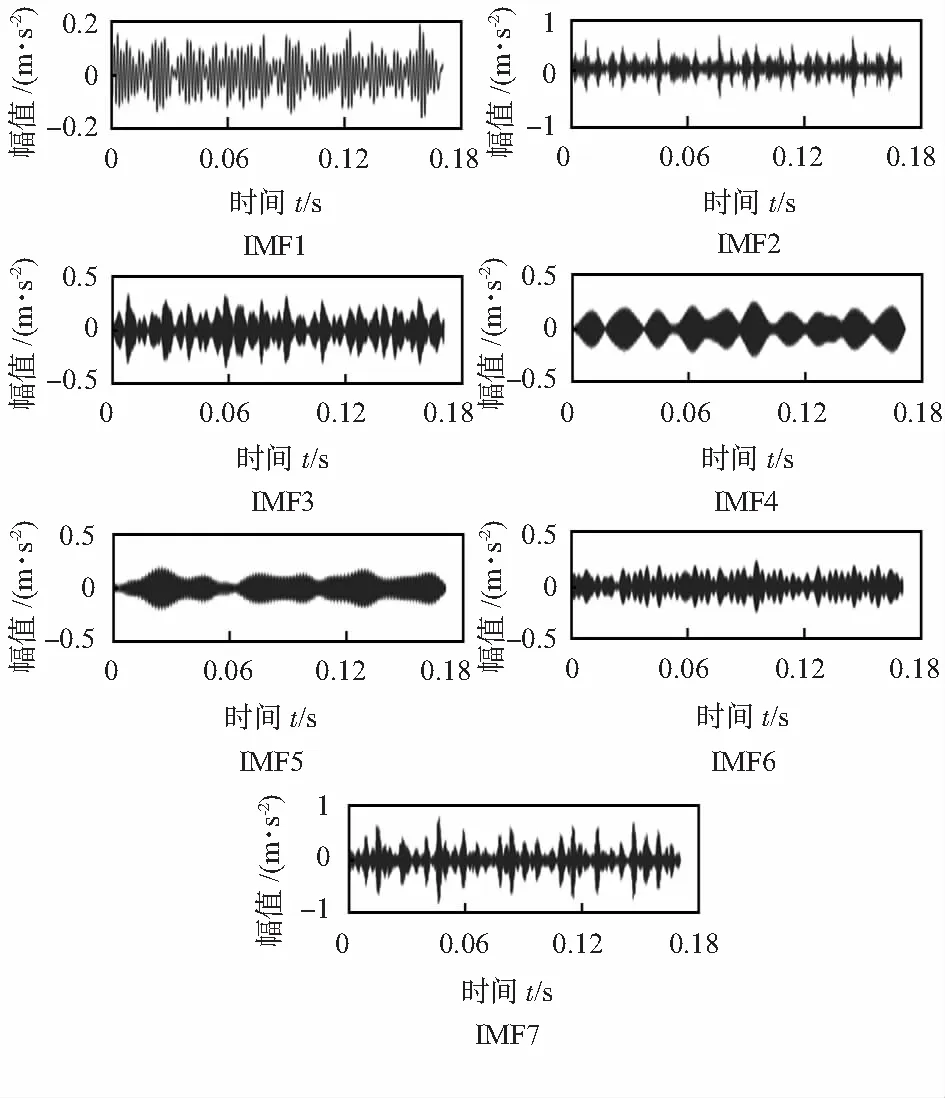
图4 内圈故障EWT分解结果

根据IMF奇异值熵的定义求取EWT分解后IMF分量的奇异值熵。为了充分捕捉信号的微弱变化,构造的Hankel矩阵的维数尽可能的大,设相空间长度为1 024,对矩阵进行处理得到奇异值熵。如表1所示为滚动轴承四种状态分别进行EWT分解后IMF分量的奇异值熵。

表1 不同状态EWT分解的奇异值熵

由表1可得,同种状态各分量的奇异值熵各不相同,表明同一采样时间内各频段的信号复杂程度不同；不同状态的奇异值熵之间也存在较大差异,表明故障类型不同,其信号复杂度不同。由此说明,IMF奇异值熵可以作为滚动轴承的故障特征。

对滚动轴承160组振动数据进行EWT分解,然后进一步求取各分量的奇异值熵组成原始特征空间R160×7。利用t-SNE算法对高维数据进行降维,得到低维特征空间R160×2,如图5(a)所示。由图可知,除了内圈故障有两个离群点外,其余状态的样本都有很好的聚类性。

2)故障识别分析

将低维特征空间R160×2数据输入到K-means分类器中进行识别,如图5(b)所示。由图可知,基于IMF奇异值熵和t-SNE的滚动轴承故障识别方法能够将滚动轴承的四种状态完全分离出来,证明了该方法的有效性。

图5 低维特征和K-means聚类结果

3.3 实验对比

1)将数据进行EMD分解,求取前7个分量的奇异值熵组成原始特征空间R160×7,将高维特征空间进行t-SNE降维,得到低维特征空间R160×2。2)采用与本文相同的方式得到原始特征空间R160×7,采用PCA对特征空间进行降维。利用K-means分类器对上述两种方法的数据进行分类,图6(a),(b)分别为三种方法的低维特征效果图和K-means聚类效果图。

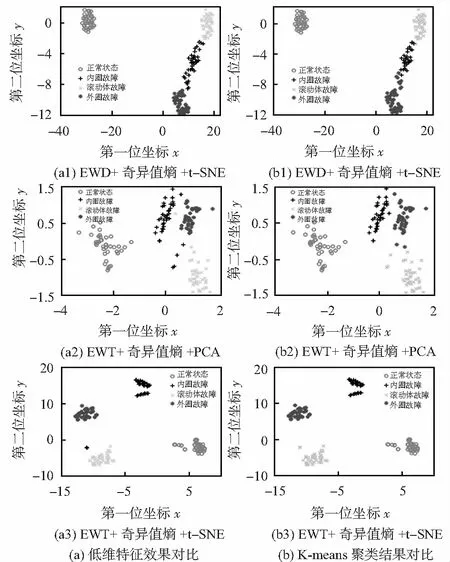
图6 实验对比结果

从图6可知,经EMD+奇异值熵+t-SNE方法得到的分类图,除了正常状态外,其余三种故障情况均出现了类间距较小的情况,故障易混叠,不利于故障类型的判别。经EWT+奇异值熵+PCA方法得到的分类图,虽然能够将滚动轴承的四种状态基本分离出来,但存在类内距较大、类间距较小的情况,容易发生混叠。相比前两种方法,基于EWT、奇异值熵和t-SNE的故障识别方法能够将滚动轴承的四种状态完全分离出来,并且类内距与类间距均达到最佳效果。

由表2可知,EMD+奇异值熵+t-SNE方法最差,EWT+奇异值熵+PCA方法次之,EWT+奇异值熵+t-SNE方法最好。

表2 不同方法的聚类精度

4 结 论

1)本文将EWT和奇异值熵相结合的方法首次应用到滚动轴承振动信号分析中,有效提取了滚动轴承不同状态下的特征向量。2)对于高维特征向量,采用t-SNE降维得到的低维特征向量,与PCA方法得到的特征向量相比,具有更好的聚类性。3)本文所提出的故障识别方法与其他两种方法相比,能够更好地区分滚动轴承不同状态,对滚动轴承四种状态的识别率达到了98.875 %,验证了本文方法的有效性。