肖洁娟，林丽双

(集美大学理学院，福建 厦门 361021)

0 引言

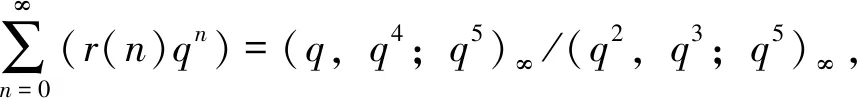
主要结论是定理1和定理2。

定理1

(1)

(2)

(3)

(4)

(5)

定理2

(6)

(7)

(8)

(9)

(10)

1 预备知识

拉马努金的一般西塔函数定义如下：

(11)

从文献[14]中可得如下两个恒等式，即

f(1，a)=2f(a，a3)，(12)

f(a，b)=(-a，-b，ab;ab)∞。

(13)

引理1

f(a，b)=f(a3b，ab3)+af(b/a，a5b3)，(14)

如果ab=cd，则有

f(a，b)f(c，d)=f(ac，bd)f(ad，bc)+af(b/c，ac2d)f(b/d，acd2)。

(15)

式(14)、式(15)这两个恒等式对定理的证明至关重要，它们的证明参见文献[14]。

引理2

φ(q)f(q4,q6)-2qψ(q2)f(q，q9)=φ(q5)f(q4，q6)-2q2ψ(q10)f(q，q9)，(16)

φ(q)f(q2，q8)-2ψ(q2)f(q3，q7)=2qψ(q10)f(q3，q7)-φ(q5)f(q2，q8)。

(17)

证明由文献[15]可得

φ(q)+φ(q5)=2(q2,q8,q10,q12,q18,q20;q20)∞/(q,q4,q9,q11,q16,q19;q20)∞,

φ(q)-φ(q5)=2q(q4,q6,q10,q14,q16,q20;q20)∞/(q3,q7,q8,q12,q13,q17;q20)∞,

ψ(q2)+qψ(q10)=(q3,q7,q10,q13,q17,q20;q20)∞/(q,q6,q9,q11,q14,q19;q20)∞,

ψ(q2)-qψ(q10)=(q,q9,q10,q11,q19,q20;q20)∞/(q2,q3,q7,q13,q17,q18;q20)∞。

利用式(13)，可得到f(q4,q6)和f(q，q9)的表达式，从而不难验证(φ(q)-φ(q5))f(q4,q6)=2q(ψ(q2)-qψ(q10))f(q,q9)。因此，对上式移项之后就可得到式(16)。同理可证式(17)。

引理3

φ(q5)ψ(q2)-qφ(q)ψ(q10)=(q;q)∞(q5;q5)∞。

(18)

2 定理1的证明

本文仅证明定理1，因为定理2的证明方法同定理1的类似。下面证明定理1。

c(n)的生成函数可以改写为

(19)

利用引理1，可得

(20)

联立式(19)～式(20)两个等式，可得

(21)

(22)

类似地，可得关系式为

H5,0(qS2)=q10f(q40,q60)f(q5,q95),(23)

H5,0(q4S3)=q20f(q10,q90)f(q5,q95),(24)

H5,0(q3S4)=q10f(q10,q90)f(q45,q55)。

(25)

提取式(21)中所有q的幂次是5的倍数的项，再运用式(22)～式(25)，并用q代替q5，可得到

其中：M1(q):=f(q8,q12)f(q9,q11)+q2f(q8,q12)f(q,q19);N1(q):=q4f(q2,q18)f(q,q19)+q2f(q2,q18)f(q9,q11)。在式(14)中分别令a=q2，b=q3，可得M1(q)=f(q8,q12)f(q2,q3)。类似地,N1(q)=q2f(q2,q18)f(q2,q3)。从而，

(26)

在式(16)中用q2代替q，并代入式(26)，可得

(27)

将a=c=-q4、b=d=-q6代入式(15)，得

f(-q4，-q6)2=φ(q10)f(q8，q12)-2q2ψ(q20)f(q2,q18)。

(28)

由式(27)～式(28)可得

至此，完成了式(1)的证明。由于式(2)和式(5)的证明与式(1)类似，这里不再给出其证明过程。下面证明式(3)～式(4)。

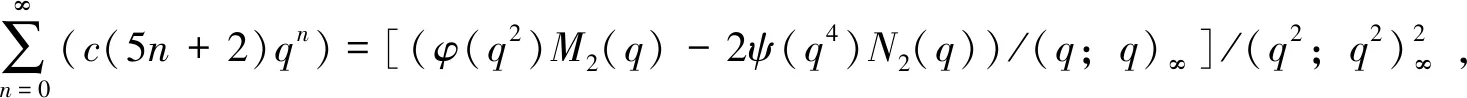
(29)

在式(17)中用q2代替q，然后代入式(29)，可得到

(30)

在式(15)中，令a=c=-q2、b=d=-q8，有

f(-q2，-q8)2=φ(q10)f(q4，q16)-2q2ψ(q20)f(q6,q14)。

(31)

联立式(30)～式(31)，可得

类似地，有如下生成函数

其中：M3(q):=q2f(1,q20)f(q7,q13)+q3f(1,q20)f(q3,q17);N3(q):=qf(q3,q17)f(q10,q10)+f(q7,q13)f(q10,q10)。利用引理1，不难得到：M3(q)=2q2ψ(q20)f(q,q4)，N3(q)=φ(q10)f(q,q4)。因此,有

(32)

由定理1与定理2，可得以下3个推论。

推论1 对于任意的正整数n,c(5n+1)=d(5n),c(5n+4)=d(5n+3)。

推论2 对于任意的正整数n，c(5n+i)>0，c(5n+j)<0，其中i=0，1,j=2，3，4。

推论3 对于任意的正整数n，d(5n+i)>0，d(5n+j)<0，其中i=0，2,j=1，3，4。