张广兴

(河北省地矿局第八地质大队测绘处, 河北 秦皇岛 066000)

0 引言

在高程控制测量中水准网平差至关重要,通常使用条件平差和间接平差[1-3]。间接平差利用未知参数消除观测值之间的不符值,通过自由极值求解未知参数的最或是值,达到平差的目的。间接平差参数设定简单,误差方程在建立过程中唯一,但未知参数个数的选定要求高,一旦选定不合适就会产生较大误差[4-10]。

条件平差是一种经典的平差方法,19世纪到20世纪之间发展的已经相对成熟。条件平差是将全部观测值的平差值作为未知数,利用多余观测数列方程,通过求条件极值求解改正数,进行平差。条件平差方程式直观简单,计算过程规律性强,但由于水准网形多种多样,导致条件平差方程不唯一[11]。自20世纪50年代开始,随着计算机的不断发展,条件平差方法也得到了很大程度的发展,研究成果相当普遍,但是由于水准网形复杂多样,条件平差方程列立不唯一,改正数的解存在多样性,在使用计算机进行处理时非常困难,由此本文提出了一种利用传递矩阵建立条件平差的算法。

1 利用传递矩阵建立条件方程

1.1 传递数矩阵的建立

假设某一水准网中水准路线数为n,水准点的个数为m,则该水准网的传递数矩阵T为:

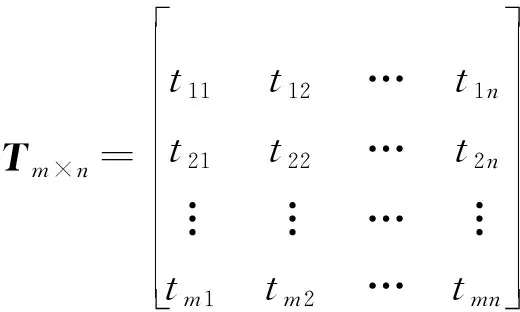
(1)

式(1)中水准路线取值为1,2,…,n,水准点从待定点开始编号,全部编号结束后紧接着对已知点编号,直到m结束。

1.2 传递数矩阵的运算规则

通过选取的水准路线的起点和终点是否已知、未知水准点的近似高程是否已经计算,计算传递数矩阵[12],运算规则为:

(1)若水准路线j的起始水准点i已知,终点水准点k未知,且该点近似高程未知,则有:

T(k,j)=1,且T(k)其余分量值为0,式中,T(k)为第k号水准点的传递向量。

(2)若水准路线j的起始水准点i未知,且该点近似高程未知,终点水准点k已知,则有:

T(i,j)=-1,且T(i)其余分量值为0。

(3)若水准路线j的起始水准点i未知,且该点近似高程已知,终点水准点k未知,且该点近似高程未知,则T(k)由两部分组成,一部分为该水准路线对终点的影响:

T(k,j)=1,且T(k)其余分量值为0。

另一部分为起点传递数向量传递给终点的,为:

T(k)=T(k)+T(i)

(2)

(4)若水准路线j的起始水准点i未知,且该点近似高程未知,终点水准点k未知,且该点近似高程未知,则T(k)由两部分组成,一部分为该水准路线对起点的影响:

T(i,j)=-1,且T(i)其余分量值为0。

另一部分为终点传递数向量传递给起点的,为:

T(i)=T(i)+T(k)

2.3 利用传递数矩阵的条件平差系数矩阵的建立

选取必要观测数t条水准路线计算待定点的近似高程,则多余观测数r为水准路线的总数n与必要观测水准路线数t的差值,利用r条水准路线建立条件方程。

假设系数矩阵A为:

(3)

假设A(s)为第s个条件方程的系数构成的行向量,若第j条水准路线未用于计算待定点的近似高程,起始水准点点号为i,终点水准点点号为k,则A(s)为:

A(s)=T(i)-T(k)

(4)

常数项W为:

W(s)=该点水准路线起点高程+高差-终点高程

(5)

2 算例分析

2.1 算例1

水准网1如图1所示。已知高程为HX=237.483 m,水准路线数n为5,水准点总个数m为4,观测高差与路线长度如表1所示。

图1 水准网1

表1 水准网1观测高差和路线长度

水准网1的水准路线的编号如表1所示,水准点的编号如表2所示。

表2 水准网1水准点点名与对应编号

利用L1、L3、L5水准路线计算待定点的近似高程,即第1、3、5号水准路线,相应确定传递数矩阵。第1、3、5号水准路线为水准路线起始水准点已知,终点水准点未知,且该点近似高程未知,则有T(1, 4)=1,T(2, 4)=1,T(3, 4)=1,其余分量值为0,所以传递数矩阵为:

(6)

第2、4号水准路线未参与传递数矩阵的计算,可以用来计算条件平差的系数矩阵和常数项矩阵。以第2条水准路线为例,起点点号为1,终点点号为2,所以可以求得:

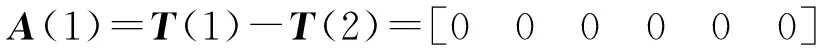
(7)

同理可以计算出:

(8)

又因为A(s)第j个分量的值为1,所以最终求得条件平差的系数矩阵为:

(9)

根据常数项W的计算公式,以W(1)为例,2号水准路线起点Y近似高程为237.483+5.835=238.018 m,终点Z的近似高程为237.483+9.640=247.123 m,可以求得:

W(1)=238.018+3.782-247.123=-0.023 m

(10)

同理可以求得W(2)=0.014 m。

所以求得常数项矩阵为:

(11)

根据条件平差过程可以求得法方程联系数K:

(12)

所以改正数V为:

(13)

这样就可以求得观测高差的改正数,对水准网1的原始测量高差进行改正后如表3所示。

表3 水准网1观测高差及其改正值 单位:m

为了比较通过传递数矩阵改正后高程的精度,以环路闭合差进行评价,选取了水准网1中的三个闭合环路,计算其改正前后环路闭合差,如表4所示。

表4 改正后环路闭合差 单位:mm

由表4可知,闭合环XYZ、XZQ以及XYZQ的环路闭合差在利用传递数矩阵改正后效果明显变好,环路闭合差都为0 mm,说明本文所用方法有效,可以在高程改正中应用。为了避免数据的偶然性,利用算例2进行验证。

2.2 算例2

水准网2如图2所示。已知高程为HA=23.0 m,HB=23.564 m,HC=23.663 m,水准路线数n为6,水准点总个数m为5,观测高差与路线长度如表5所示。

图2 水准网2

水准网2的水准路线的编号如表5所示,水准点的编号如表6所示。

表5 水准网2观测高差和路线长度

表6 水准网2水准点点名与对应编号

利用第3、4两条水准路线计算待定点的近似高程,相应确定传递数矩阵。第3、4这两条水准路线为水准路线起始水准点已知,终点水准点未知,且该点近似高程未知,则有T(1, 4)=1,T(2, 3)=1,其余分量值为0,所以传递数矩阵为:

(14)

第1、2、5、6条水准路线未参与传递数矩阵的计算,可以用来计算条件平差的系数矩阵和常数项矩阵。以第1条水准路线为例,起点点号为2,终点点号为1,所以可以求得系数矩阵A为:

(15)

根据常数项W的计算公式,求得常数项矩阵为:

(16)

根据条件平差过程可以求得法方程联系数K:

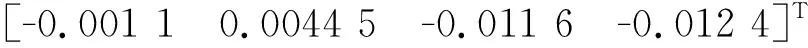
(17)

所以改正数V为:

V=QATK=
[0.001 1-0.004 450.005 5-0.000 36
0.011 60.012 4]T

(18)

对水准网2的原始测量高差进行改正后如表7所示。

表7 水准网2观测高差及其改正值

同样,参考算例1,采用水准网2中的三个闭合环进行评价,改正后效果,如表8所示。

表8 环路闭合差 单位:mm

由表8可知,闭合环ADE、BDE以及ABD的环路闭合差在改正前分别为10 mm、-7 mm、3 mm,利用传递数矩阵改正后效果明显变好,环路闭合差分别为5 mm、-4 mm、1 mm,证明了利用传递数矩阵的条件平差的有效性。

3 结束语

基于条件平差和间接平差本身计算过程中存在的问题,本文提出了一种利用传递数矩阵建立条件方程的算法,利用传递数的运算规则,解决了条件方程建立过程中多样性的问题,采用两个算例,对改正后结果的环路闭合差进行比较,算例1通过改正之后三个环路闭合差全部为0,算例2在改正后三个环路闭合差为5 mm、4 mm、1 mm,效果明显变好,两个算例证明了本文所用方法的有效性,在实际应用中具有参考价值。