李方琦

( 北京邮电大学 理学院, 北京 100089)

由于交易市场的扩大、客户需求的差异以及金融衍生品市场的完善，金融机构涉及到多种期权。在众多的期权中，除了标准欧式和美式期权外，还有许多基于标准期权的奇异期权[1]。由于奇异期权可以根据客户的不同需求进行设计，交易方式和价格比标准期权更加灵活，结构比标准期权更加独特，风险管理能力更强。随着奇异期权在金融市场中地位的不断提高，有必要对奇异期权的定价进行研究。篮子期权[2]是一种奇异期权，是一种多资产期权，通常用于许多外汇交易中进行对冲。多重标的资产价格的加权平均值决定了篮子期权的到期收益率。一般来说，篮子期权的成本效率更高。因此，本文研究股票价格服从Heston波动率模型[3]的一篮子期权，推导期权价格满足的偏微分方程(PDE)。

大多数基于期权定价的连续时间模型没有闭合解。即使有闭合解，由于其特殊的形式，也很难快速求解。因此，在许多情况下，使用数值方法来解决这个问题，如蒙特卡罗、二叉树模型、三叉树模型等。多伦多大学的辛顿在2006年首次提出了深度学习的定义。它是以样本数据为基础，通过一定的训练方法进行机器学习的过程[4]。从此，深度学习的序幕拉开。Jentzen等[5-6]克服确定性数值逼近方法的局限性(维度诅咒)，提出了一种基于深度学习的高维数值逼近方法。在高维篮子期权数值解研究较少的基础上，本文将深度学习方法应用于篮子期权定价。

1 模型介绍

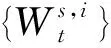
假设：

(a) 税收和交易成本可以忽略不计；

(b) 没有套利；

(c) 标的资产不分红，交易可以无限分割；

(d) 无风险收益率r是一个常数。

波动率满足Cox, Ingersoll and Ross提出的短期收益率模型：

其中：k是常数，并且每个θi(方差过程的平均水平)也是常数。

一篮子期权[2]在T时刻的价格定义为

其中K是期权的执行价格。通过风险中性定价，一篮子期权在t时刻的价格为

通过Feynman-Kac公式[7],期权价格F(t,s,v)满足下列PDE：

(1)

本文的目标是计算式(1)中的期权价格F(t,s,v)。

2 算法描述

为了近似式(1)中的F(t,s,v)，本文简单地介绍[5]中提出的基于深度学习的倒向随机微分方程(BSDE)求解算法。

2.1 算法的理论基础

假设(Ω,F,P*)是一个给定的概率空间,T>0,l∈,并且函数F=F(t,x)∈C1,2([0，T〗×l,)满足：

(2)

式中：f:l××l→和g:l→是连续函数；μ:[0,T]×l→l和σ:[0,T]×l→l是Lipschitz连续函数。

假设W:[0,T]×Ω→l是一个l维布朗运动，=(t)t∈[0,T]是定义在(Ω,F,P*)上的流(filtration)。E⊂l是单连通区域。随机过程Y:[0,T]×Ω→和Z:[0,T]×Ω→l满足下列方程：

(3)

偏微分方程(2)和随机微分方程(3)的关系为

(4)

方程组(4)中第一个方程通常称为Feynman-Kac公式[8]。

2.2 算法概述

简要介绍基于深度学习的数值BSDE算法[6]。首先由一组FBSDE开始：

对于上述前向和倒向过程，使用Euler scheme[9]和Milstein scheme[10]后得到：

Xti+1≈Xti+μ(ti,Xti)(ti+1-ti)+σ(ti,Xti)(Wti+1-Wti)，

(5)

Yti+1≈Yti-f(Xti,Yti,Zti)(ti+1-ti)+Zti(Wti+1-Wti)。

(6)

这里，把BSDE转化为前向过程。这组过程在本文中有如下解释：Xti由标的资产的价格和波动率Sti,Vti构成；Yti是期权的价格(这点由Feynman-Kac公式可得)；Zti代表ti时刻的Yti对Xti的偏导数。

算法的步骤可简要概括为：

第一步：从标的资产在0时刻的价格X0和猜测的初始值Y0,Z0开始。在数值BSDE算法中，采用神经网络结构，用参数θ来逼近各时间点的Zti项。

第二步：使用式(5)、式(6)和神经网络近似得到的Zti计算每一个Xti和Yti,直到T时刻。

第三步：在终端时刻，定义损失函数为E[(YT-g(XT))2]。采用随机梯度下降法，通过迭代到Y0,Z0和θ的最优值，使损失函数最小化。

3 数值模拟

3.1 d维篮子期权

把一篮子期权定价问题代入2.2节算法中，有

向量ei∈l,满足

e1=(1,0,0,…，0,0)，e2=(0,1,0，…，0,0)，…，el=(0,0,0,…，0,1)，对任意t1,t2∈(0，T]，x=(x1,x2,…，xl)=(s1,…，sd,v1,…，vd),ω=(ω1,ω2,…，ωl)∈l,在篮子期权中，关于x的迭代函数[9-10]式(5)为

且一篮子期权的价格F(t,s,v)满足的偏微分方程为式(1)。

3.2 数值结果

本文的每个数值模拟都是使用TENSORFLOW 1.8.0在PYTHON中执行的，继续讨论神经网络求解衍生期权定价问题。

表1 期权价格随迭代步数的变化Tab.1 Changes of option prices with steps

为了得到期权价格F(t=0,x=(100,…,100,1,…,1))的近似值，将本文算法程序独立运行5次，记下每次运算期权价格和损失函数的变化。在计算过程中以蒙特卡罗方法得到的期权价格8.125作为精确解来计算一阶相对误差。

图1 5次模拟期权价格的变化情况Fig.1 Changes of option price in 5 simulations

5次模拟期权价格随迭代步数的变化关系如图1所示，为了使趋势更加明显本文使用了lg坐标。图1中5条曲线最后接近于同一数值，说明该算法稳定。

4 结束语

随机微分方程和偏微分方程在金融衍生品定价模型中有着广泛的应用，通常它们的解析解是无法得到的，设计和分析能够近似求解的数值方法一直是活跃的研究课题。本文系统地描述了利用深度学习求解篮子期权的偏微分方程。实验结果表明，该方法是准确稳定的，有助于将该方法应用到其他期权定价中。