陈腾飞， 何 欢， 何 成， 陈国平

(1. 南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016)

(2.南京航空航天大学无人机研究院 南京，210016)

引 言

在时变系统辨识领域，目前对线性系统的研究比较深入。现有各种时域、频域方法，大多通过线性系统成熟的理论将线性时不变结构系统的模态分析理论推广到时变系统[1-3]。但是，几乎所有的实际工程结构都呈现出非线性特性，在系统辨识中同时考虑系统的非线性和时变特性难度较大[4-5]。近年来，在系统控制、信号处理等领域中，国内外学者已经开始研究，并做出一些有意义的尝试[6-8]。

根据模型不同，非线性时变系统辨识方法可以分为两大类：第1类是神经网络模型方法，第2类是非线性参数模型方法[9]。Ahmed-Ali等[10]基于径向基函数神经网络发展提出一种自适应辨识方法。He等[11]基于“短时时不变”假设，将非线性自回归滑动平均(nonlinear autoregressive moving average, 简称NARMA)模型应用于非线性时变系统辨识问题。一些用于线性时变系统的信号处理方法也被应用在非线性问题中。Li等[12]结合B样条基函数和正交前向回归(orthogonal forward regression, 简称OFR)算法，有效地追踪线性系统中的慢变及快变参数，并将此方法结合时变NARMA模型，用于非线性时变系统问题，得到了较好的辨识效果[13]。

非线性时变系统辨识包括非线性的定位、非线性类型的确定以及参数估计，其中非线性定位方法已经发展成熟。目前，大多研究默认非线性类型已知，并没有涉及这方面的讨论。因此，迫切需要新的方法确定系统中时变非线性的所有信息，包括具体位置、类型和系数。正交三角分解QR是回归量正交化常用手段，可以用于消除不同变量之间的耦合关系。本研究将QR分解应用于连续时间MDOF模型中，准确辨识出系统的所有线性及非线性时变特征。

在动力学分析中，实际工程结构通常被离散为多自由度结构系统。根据实际情况，可以采取不同的离散方法，例如集中质量系统，有限单元方法等。文中假设结构可以精确离散化为多自由度系统，并且所有自由度上的运动被精确测量。文中简单描述非线性时变MDOF系统的数学模型；根据自由度将结构系统分解为不同子系统；结合QR分解和ERR计算，对系统非线性时变参数进行辨识；最后，通过数值算例来验证辨识方法的精度。

1 非线性时变MDOF系统数学模型

通常，n自由度线性时变系统的运动方程可以写为

(1)

(2)

由式(2)，系统第i个自由度上的运动方程为

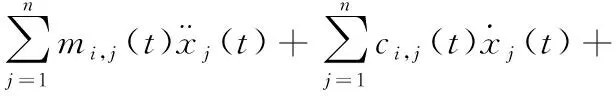
(3)

在MDOF系统中，每个自由度的运动不仅由自由度上的载荷分量决定，还受到其他自由度运动连接的影响，而系统辨识的意义在于确定不同自由度之间这些未知连接关系。用一组基函数对系统中非线性恢复力展开

(4)

在一般的动力学系统中，多项式基函数可以拟合多种类型的非线性恢复力，例如三次非线性刚性力、立方根型非线性刚性力等。将式(4)代入式(3)可得

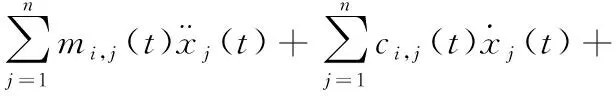
(5)

(6)

其中：βi,k(t)为时变系数。

(7)

由“短时时不变”假设可知，βtn,i,k即为式(6)中时刻tn下的参数值，即βi,k(tn)=βtn,i,k。若系统位移、速度、加速度以及外载荷均可准确测得，则系统参数辨识问题转化为标准回归问题。对不同时刻tn，若时刻点数大于未知参数的数量，则所有线性和非线性参数可通过求解式(7)中方程确定。在此之前，需要解决的一个重要问题是如何确定式(6)中基函数具体形式和总数。对此，文中会提出一个基于QR分解的子系统算法，有效解决此问题。

2 非线性时变MDOF系统的子系统描述

时不变集中质量MDOF系统的质量矩阵是对角矩阵，相似地，时变集中质量MDOF系统的质量矩阵可以表示成以下形式

(8)

(9)

因此，式(5)可以改写为

(10)

尽管式(10)在形式上与式(5)类似，但是式中所有项均有具体的物理意义，包括连接的位置及形式。例如，k'i,j(t)ξi,j表示mi和mj之间存在线性弹簧连接。因此，文中将采用式(10)中的模型。

同式(6)中原理，式(10)中所有线性和非线性项可以写成统一形式，式(11)可看作一个包括系统线性和非线性连接黑箱模型

(11)

其中：K为线性和非线性项总数；θi,k(t)为模型中时变系数；φi,k为和mi相关的相对位移和速度的任意形式的函数。

在本研究中，将采用多项式基函数展开，因此式(11)可以改写为

(12)

引入“短时时不变”假设，系统可以表示为

(tm-Δt/2≤t≤tm+Δt/2)

(13)

其中：质量mtm,i和多项式系数γtm,j,k,p,q在此时间区间内均为常数，且

(14)

在式(13)中，如何确定多项式项成为新的难题，因为不是所有的多项式项都是模型中所需要的，这主要取决于系统中非线性特性，包括位置以及非线性的类型，这些信息正是所缺乏的。因此，引入一个新的方法以确定式(13)中多项式项，并将参数估计简化为每个时间区间内的标准回归问题。为方便起见，式(13)可以写为更加简洁的形式

(15)

3 MDOF子系统非线性时变参数辨识方法

在式(15)的辨识问题中，通过一种基于QR分解的方法，从所有的多项式项中确定模型所需的重要项，并对所选项的系数进行估计。通常，重要项的确定分为两个步骤[11]。首先，需要确定多项式的最高阶，即式(13)中的L。显然，阶次越高，多项式基数拟合非线性模型的能力越强。但是出于计算成本的考虑，常使用较低阶次的多项式基函数，具体可通过比较不同阶次下的拟合精度来确定。与之相比，第2个步骤是在确定最高阶次的情况下，确定模型所需的重要项，是本节讨论的重点。应用QR分解确定重要项的过程：①回归量正交化，消除变量之间的相关性；②通过ERR确定模型所需的重要项；③估计参数。

式(15)中短时区间[tm-Δt/2,tm+Δt/2]内采样点总数记为N，则方程可以改写为如下矩阵方程的形式

F=ΦΘ+Η

(16)

其中

为了将回归量正交化，对回归矩阵Φ进行QR分解

Φ=QR

(17)

其中:R为K×K阶的上三角矩阵且对角元素为正;Q为N×K阶的上三角矩阵。

R矩阵可以作如下分解

R=DA

(18)

其中:D为一个K×K阶对角矩阵，其元素为R矩阵对角线元素;A为K×K阶单位上三角矩阵，即对角元素均为1。

因此，式(17)可以改写为

Φ=WA

(19)

将式(17)代入式(16)可得

F=Wg+H

(20)

其中：g=AΘ。

式(20)可以改写为

(21)

若对F自身作内积运算〈F,F〉，将式(21)代入可得

(22)

式(22)等号两边同时除以〈F,F〉可得

(23)

ERRj定义为

(24)

其中：gj=〈wj,F〉/〈wj,wj〉。

从所有候选多项式中确定模型所需的重要项，各项的ERR可以提供一个标准。在ERR计算的每一步中，具有最大EERj的候选项会被作为重要项加入模型。若给定公差常数ρ，如果以下条件满足，此重要项选择过程将在第Ks步停止

(25)

这里的ERR计算具有较高的效率，可以用来构造出形如式(15)的数学模型，避免所有的非重要项，有利于计算。

至此，文中提出的系统辨识过程可以总结如下。

1) 分别对MDOF系统不同的离散点施加外载荷并测量系统响应。

2) 确定多项式基函数最高阶，得到含有K个候选项的模型，并确定ρ数值。

3) 计算各候选项ERR，具有最大ERR的候选项作为重要项加入式(15)中的模型。

4) 在ERR计算的第k(k≥2)步，在剩余候选项中选择具有最大ERR的项作为模型的第k项。若条件式(25)满足，继续步骤5；否则，令k=k+1，重复此步骤。

5) 完成ERR计算，得到由Ks项构成的模型，系统参数估计如下

(26)

其中：As为一个Ks×Ks单位上三角矩阵;gs向量由gk(k=1,2,...,Ks)构成。

4 算例分析

4.1 3DOF集中质量系统辨识

本节通过一个非线性时变MDOF集中质量系统辨识的算例，说明提出的方法的精度和效率。若输入、输出数据全部测量，可以通过上一节描述的方法对形如式(5)的模型进行辨识。

考虑如图1所示的3自由度系统。系统质量分别为m1=-0.01t+2.5 kg，m1=1 kg和m3=1.5 kg。系统中线性刚度弹簧为k1=k2=k4=1 N/m和k3=-0.03t+4 N/m，线性阻尼为c1=c2=c3=c4=0.1 N·s/m。另外，在m2和m3之间有一个三次非线性刚度knl=3+0.000 5t2N/m3。在这些系统参数中，m1,k3和knl为含时变特性。依次单独对3个集中质量进行激励，其中外激励为用方差σ2=25的零均值平稳高斯白噪声表示的集中载荷。用四阶Runge-Kutta方法分别对系统响应进行求解，采样频率为100 Hz。在“短时时不变”假设下，每个时间区间内有1 000个时刻点参与计算，即Δt=10 s且5 s≤tm≤95 s。考虑到测量噪声的影响，在系统响应数据中添加3%高斯干扰。当噪声较大情况下，通过测量加速度积分求速度及位移，会导致误差。因此，文中假设各自由度响应数据(包括位移、速度及加速度)均可直接准确测量。

首先，需要在较多候选多项式中确定模型的重要项。在本算例中，多项式基函数的最高阶L=9，图1所示的3自由度系统可以由形如式(13)中的子系统模型描述，在每个子系统中，由最高阶为9的多项式基函数构成最初的子系统方程。通过ERR计算，在5 s≤tm≤95 s内平均ERR大于ρc=0.005%的多项式将作为此模型的重要项，不同子系统的ERR结果如表1所示。

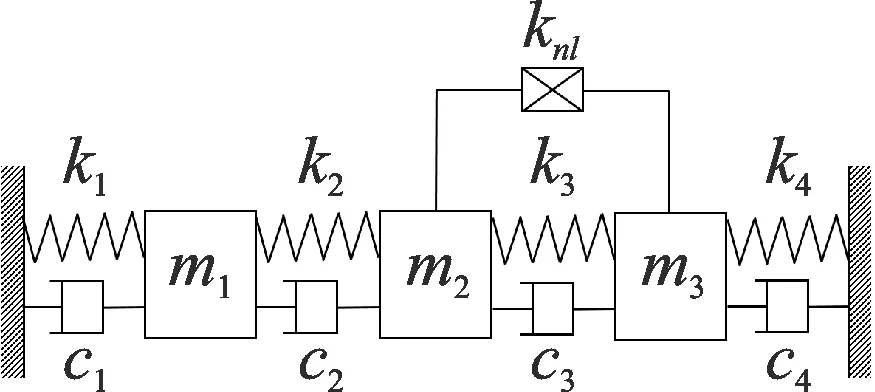
图1 3自由度集中质量系统Fig.1 The 3DOF lumped mass system

表1子系统1中所有的项均为线性项，非线性项均在ERR计算中被忽略，这说明作用在m1上的恢复力均为线性恢复力，这与图1所示一致。子系统1中的辨识结果如图2所示，包括质量m1和m1相关的所有线性连接(红色实线表示实际参数时间曲线，黑色点划线表示辨识出的曲线)。图2(a)表明质量m1辨识结果准确，包括其时变特性。为了定量分析辨识结果的精确度，将辨识出的曲线最小二乘拟合为时间的线性函数曲线，拟合曲线参数与实际质量m1比较，计算误差。拟合的曲线在图2(a)中用蓝色虚线表示，其参数及误差如表2所示。拟合直线与真实曲线接近，斜率和初值的误差均小于5%。由图2(b)～(e)可知，对子系统1中的线性刚度和线性阻尼识别精度相当高，4条辨识时间曲线与实际常参数十分接近。

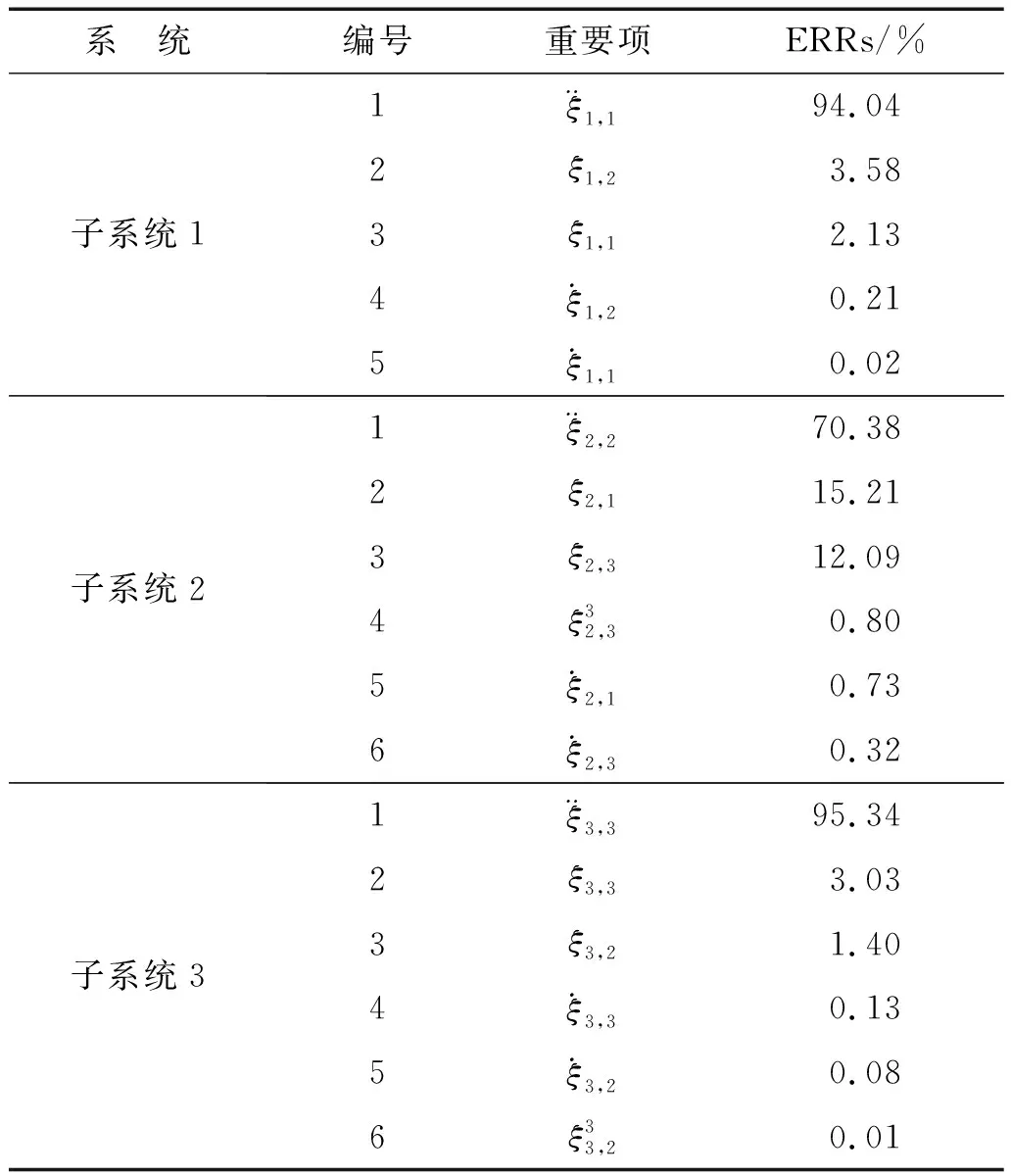
表1 各子系统中ERR结果Tab.1 ERRs of Terms in the Subsystems

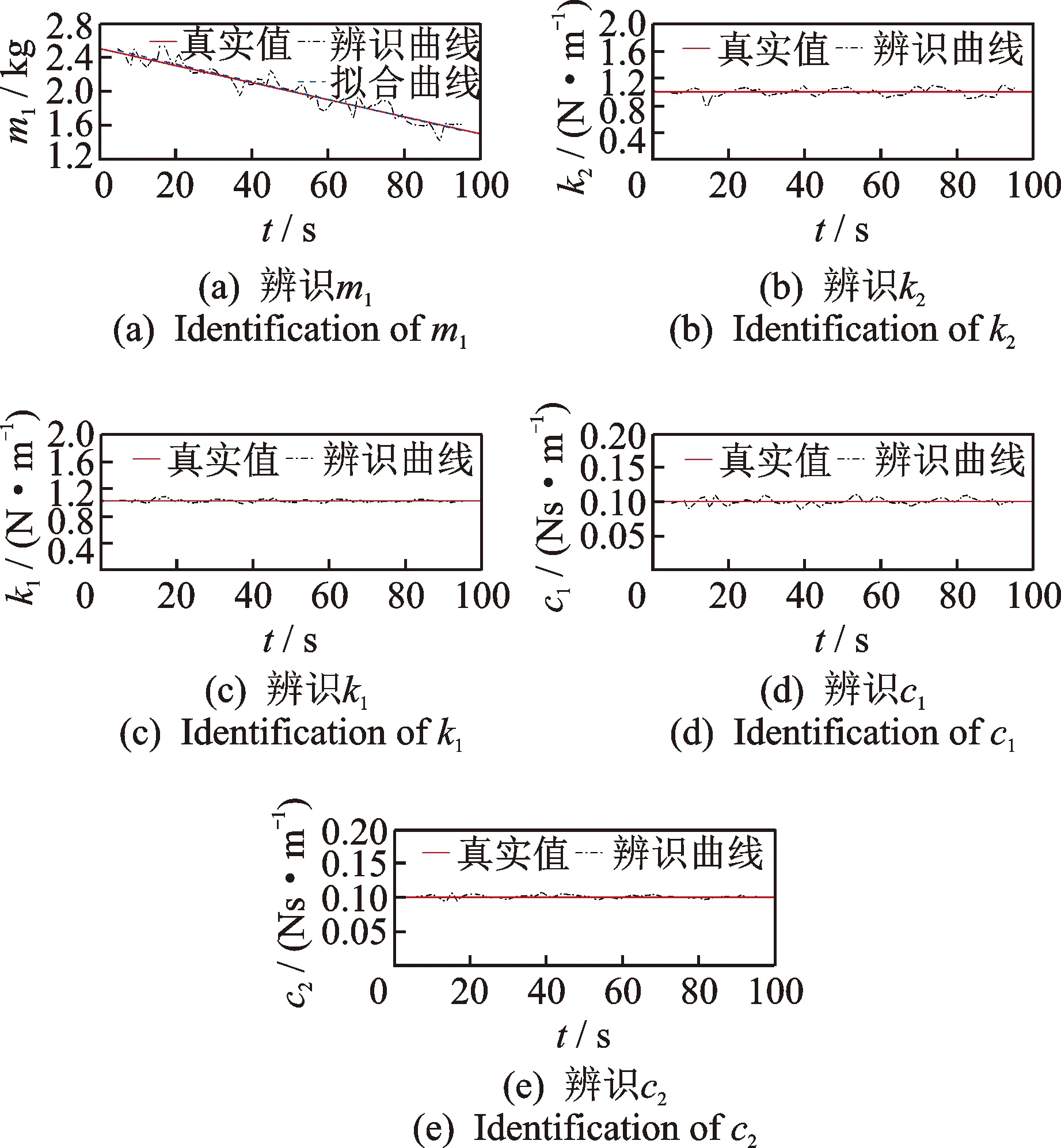
图2 子系统1辨识结果Fig.2 Identification result of subsystem 1

表2 子系统1中m1时间曲线参数Tab.2 Parameters in the Time Expression of m1 in subsystem 1

在表1子系统2中，第2,5项代表m2和m1之间的线性刚度和线性阻尼，第3,6项代表m2和m3之间的线性刚度和线性阻尼，第4项代表m2和m3之间的非线性刚度连接，这与图1所示的结构特性相吻合。子系统2的辨识结果如图3所示。在这个子系统中，存在线性时变刚度k3和非线性时变刚度knl。为定量分析上述两个时变参数辨识结果的精确度，将k3的辨识结果最小二乘拟合为时间的线性函数，将knl的辨识结果拟合为时间的二次函数，拟合项的系数及其误差如表3所示。拟合曲线与真实曲线很接近，系数误差均低于5%。

图3 子系统2辨识结果Fig.3 Identification result of subsystem 2

表3 子系统2中辨识时间曲线参数Tab.3 Identified parameters in the time expression in subsystem 2

由表1子系统3可知，在子系统3中时变参数k3和knl也被确定，分别由第3和第6项代表，子系统3的辨识结果如图4所示。同样地，对时变参数k3和knl辨识结果定量分析，结果如表4所示，由图5(c),(f)可知，用蓝色虚线表示的拟合曲线几乎与参数实际曲线重合，表明辨识精度很高。

图4 子系统3辨识结果Fig.4 Identification result of subsystem 3

图5 机械臂结构Fig.5 Mechanical arm structure

表4 子系统3中辨识时间曲线参数Tab.4 Identified parameters in the Time expression of k3 in subsystem 3

4.2 机械臂结构辨识

图5中机械臂结构运动方程可以写为

(27)

(28)

时变阻尼矩阵为

C(t)=

(29)

这里包括系数为0.005的比例阻尼。

非线性恢复力矩向量为

(30)

外载荷向量为

(31)

假设两个移动质量块位移的表达式为

ri=0.5+0.3sin(πt) (i=1,2)

(32)

两杆的初始角度为

(φ1,φ2)=(π/4,0)

(33)

分别用方差σ2=25的零均值平稳高斯白噪声表示的力矩载荷对两个子系统进行激励。用四阶Runge-Kutta方法分别对系统10 s内响应进行求解，采样频率为100 Hz。

表5 杆1子系统中kn l辨识结果Tab.5 Identification Results of kn l

图6 立方根型非线性扭转刚度knl辨识结果Fig.6 Identified result of the cube-root stiffness knl

上述两个数值算例结果表明，笔者提出的方法可以准确地识别出时变MDOF系统中非线性特性，确定非线性位置及类型，并估计出系统参数的时间曲线。不同自由度之间的连接可以在不同子系统中分别辨识。值得注意的是，有些系统的非线性特性取决于外载荷的大小和频率，为了能在合理范围内对实际结构系统进行近似，外载荷最好具有宽幅、宽频，以激发系统的非线性特性。

5 结束语

基于QR分解和ERR计算，发展出一个新的非线性时变系统辨识方法，将MDOF系统分为不同的子系统，在不同子系统中，对非线性及时变连接进行定位、估计。该方法主要优势在于，无需关于系统的先验知识，直接在连续时间模型中准确辨识非线性时变参数。此方法需要测量模型中各自由度的响应数据，对于大型工程结构，首先要对模型进行降阶处理。