孙华飞，曾澍楠

(北京理工大学数学与统计学院，北京 100081)

信息几何用于研究非线性与随机性的问题，其基本的思想是把所要研究的问题纳入黎曼流形框架，利用几何方法研究问题。在人工智能、大数据时代，人们要面临随机性、非线性、高维度的复杂信息。如果利用传统的欧氏空间的方法来处理复杂信息往往会带来较大的误差，达不到需要的精度。信息领域中的许多实际问题是非线性和随机性的，而信息几何恰好成为解决上述问题的有效的工具。Rao[1]提出Fisher矩阵可以充当黎曼度量，使得概率分布集合成为一个黎曼流形；Amari[2-4]计算了正态分布全体所形成的黎曼流形，发现它是一个双曲空间，这成为他创立信息几何的原动力，随后与其合作者提出了对偶联络的概念，由此创立了信息几何的理论框架，成功地应用于计推断、信号处理、图像处理、神经网络、最优控制、机器学习等领域。Nielsen等[5]提出的矩阵信息几何是对经典信息几何的重要补充，一些深刻的数学手段诸如李群、纤维丛、拓扑学等派上用场，为解决非随机性问题提供重要的数学手段[5-6]。从20世纪80年代信息几何诞生至今，信息几何的理论与应用研究不断丰富，应用范围逐渐扩大。随着最优传输理论与信息几何的融合，信息几何不断焕发着青春，为解决信息领域中亟待解决的瓶颈问题提供了可能。为此，介绍信息几何从最初理论框架到近几年最新成果的发展过程，期望对信息几何感兴趣的学者有所帮助。

1 统计流形与Fisher 信息矩阵

流形的概念可以看成是欧氏空间中的曲线和曲面的推广，例如球面、环面等都是熟知的流形，而由n阶可逆矩阵全体组成的集合，一般线性群GL(n,R) 也是一个流形。统计流形的概念[2-3,5,7-9]定义如下。

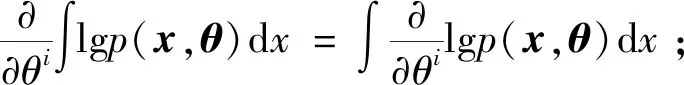
称满足上述条件的流形M={p(x,θ)}为统计流形。

设TpM表示流形在p点处的切空间，在其上面可以定义一个黎曼度量——Fisher信息度量：

(1)

式(1)中：E表示函数的数学期望。于是M关于度量g=[gij(θ)]成为一个黎曼流形。对于一元正态分布构成的流形M={p(x,θ)}，其中

(2)

式(2)中：μ、σ2分别表示分布的平均值与方差。Amari计算了M的高斯曲率，发现它的高斯曲率是-1/2，即此时M成为一个双曲空间。通过把概率分布纳入黎曼几何框架，可以利用对偶联络、测地距离、曲率、自然梯度等几何结构来刻画随机的非线性问题。

1.1 联络

对应于欧氏空间中的方向导数，在流形上需要引入联络的概念。联络可以看成是流形上的求导数运算，它联系流形上两个不同点处的切空间，满足线性与莱布尼兹运算法则。

设TpM表示流形M在点p处的切空间：

(3)

整个运算在p点的切空间TpM上进行。设x:(-δ,δ)→M为光滑曲线，如果

(4)

等价地

(5)

ξ:TpM×TpM×TpM→TpM

(6)

或者：

ξ(X,Y)Z=XYZ-YXZ-[X,Y]Z

(7)

式中:X、Y、Z表示M上的向量场;[·,·]表示李括号，满足[X,Y]=XY-YX。截面曲率定义为

(8)

式(8)中：g表示Fisher信息度量。

黎曼联络(Levi-Civita联络):

(9)

黎曼联络满足无挠性和相容性，无挠性意味着对称性，而相容性意味着在平行移动下切向量的长度保持不变。

如果一个流形的曲率和挠率都恒为零，则ξ(X,Y)Z=0,T(X,Y)=0，如同欧氏空间那样，既不弯曲，又不扭曲，则称该流形是平坦的。

现在给出曲率的另一个直观解释。流形上一个切向量沿着一个闭曲线平行移动一周后保持原状，说明该流形是一个欧氏空间，即欧氏空间中的向量做平行移动后大小和方向均不变。反之，如果改变了状态，说明该流形不是平坦的欧氏空间，而由平行移动前后的差可以刻画流形的曲率。

对于随机的信息几何来说，黎曼联络过于严苛，无法使用。为解决这个问题，Amari与合作者提出了关于度量g的对偶仿射联络、(*)，满足

(10)

式(10)中：X、Y、Z为流形M上任意一点处的切向量。可以看出，当2个联络相同时，X和就是黎曼联络。

上述对偶联络是信息几何框架的支柱，而且实际应用就由此衍生。Amari[2-4]与合作者提出了更加具体的对偶联络，可以用于各种应用。由数学期望来定义下面的(α)联络:

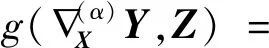
(11)

式(11)中:α为任意的实数。可以验证(α)与(-α)是对偶联络，而且(α)是对称的联络。用分量可以表示为

(12)

式(12)中：Γijk为黎曼联络系数，且

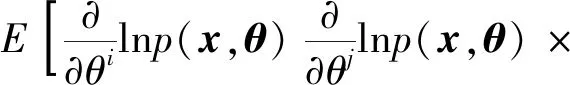
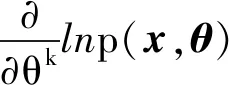
(13)

式(13)中：θ为统计量参数。

众所周知，欧氏空间上一点到其中的一个子空间的距离就是该点到子空间的投影距离。而对于一个弯曲的空间上一点到其子空间的投影情况将会如何，这对母空间和子空间都有要求。设[S,g,(α),(-α)]为一个对偶平坦的黎曼流形，M为S的子流形，利用(α)测地线与(-α)测地线，可以获得S中的点到M的投影，此方法可以用于解决许多实际问题。

设[S,g,(α),(-α)]是对偶平坦的黎曼流形，则存在对偶坐标系θ、η和对偶势函数ψ、φ使得：

(14)

式(14)中：gij表示矩阵[gij(θ)]拟矩阵的分量，且

(15)

进一步，可以定义散度，即衡量p、q两点差异的距离函数：

D(p,q)=ψ(θp)+φ(ηq)-θpηq

(16)

该函数满足非负性，不满足对称性和三角不等式，且D(p,q)=0的充要条件是p=q。

当密度函数满足：

p(x,θ)=exp[θ·x-ψ(θ)]

(17)

此时，p(x,θ)称分布为指数分布族。在Fisher度量以及(α)下，可以获得相应的几何结构：

(18)

(19)

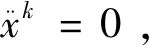
1.2 距离函数与测地距离

距离函数的选取，取决于问题的载体。例如测量中国与美国的航线距离时，不能利用欧氏距离，而是用测地距离。

对于欧氏空间Rn中的两点x和y，利用欧氏距离来定义两点间的距离：

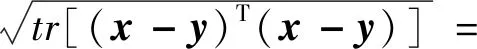
(20)

在经典的信息几何理论中一般不使用欧氏距离，而使用Kullback-Leibler散度：

(21)

测量两个密度函数p(x,θ)与q(x,θ)的差异。值得注意的是，KL(p,q)关于p(x,θ)与q(x,θ)并不对称，而且p=q的充要条件是KL(p,q)=0。一个对称的距离函数JS散度定义为

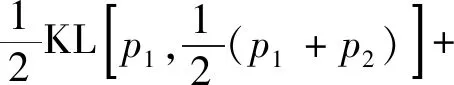
(22)

作为Kullback-Leibler散度的推广，Bregman散度表示为[10]

Bφ(x,y)=φ(x)-φ(y)-(x-y)·φ(y)

(23)

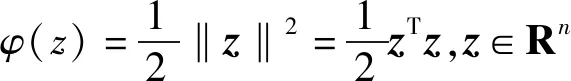
还有著名的与最优传输密切相关的Wasserstein 距离函数[11]：

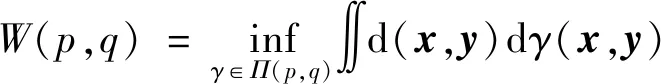
(24)

式(24)中：inf表示下确界;p(x)和q(x)为2个概率密度函数，γ(p,q)为p和q联合密度函数；d(x,y)表示一个成本函数，表示从x到y的成本，可以表示各种范数。Π(p,q)为p,q联合密度函数的全体，满足：

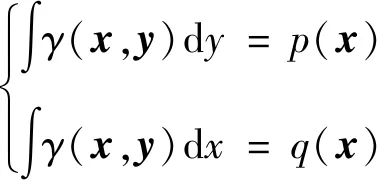
(25)

值得注意的是，Wasserstein 距离函数并不需要给出参数表示。

对于抽象的黎曼流形M,带有黎曼度量g，其距离函数定义为

d(p,q)=inf[L(γ)]

(26)

式(26)中：γ为M中链接p、q的分段光滑曲线的长度。该距离在实际应用中非常困难，而对于具体的流形，例如矩阵流形等可以给出显式的表达，便于计算。

以一般线性群GL(n,R)的子流形——正定矩阵流形SPD(n)为例，定义几种度量和距离。在SPD(n)上定义欧氏度量(平坦度量)：

g(X,Y)=tr(XTY)

(27)

式(27)中：X,Y∈TASPD(n)；A∈SPD(n)，距离函数定义为

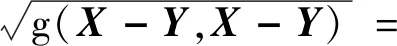
(28)

在该度量下，经过A、B两点的测地线可以表示为

γ(t)=A+t(B-A)

(29)

式(29)中：t表示系数。

显然，该测地线无法保证永远在SPD(n)上，这就导致无法利用测地距离研究问题。

如果定义左不变度量

g(X,Y)=tr[(A-1X)T(A-1X)]

(30)

式(30)不是一个平坦的黎曼度量，其测地线为

(31)

式(31)中：S属于A点的切空间。可以看出，对任意的t都可以保证测地线都能保证在SPD(n)上[12-13]。经过计算，可以获得连接SPD(n)上任意两点A、B的测地距离：

(32)

类似地，可以在SPD(n)上定义对数欧氏黎曼度量[13]

gA(X,Y)=tr{[(dln)AX]T(dln)AY}

(33)

由此获得经过A、B的测地距离:

(34)

及利用纤维丛获得的黎曼度量[14]:

(35)

式(35)中：Y=KX+XK。SPD(n)上任意两点A、B的测地距离为

(36)

对于其他流形，例如特殊欧几里得群[15]：

(37)

可以定义左不变黎曼度获得连接P1和P2两点的测地距离

(38)

1.3 梯度算法

许多实际问题可以归结为求解带有约束的目标函数的最优值。对于定义在欧氏空间上的目标函数，可以利用梯度下降法求解其局部极小值。对于求解黎曼流形上的目标函数的最优值时，就不能用梯度，而负的黎曼梯度方向才是最速下降方向。黎曼梯度的好处在于，它可以使迭代的步数减少，缓解陷入局部极小的现象。与牛顿方法假设二次形式的目标函数不同，黎曼梯度方法在形式上比较简单。另外，自然梯度在线学习给出了渐近统计意义下的Fisher有效估计，因此它渐近等价于最优批处理过程[16]。各种梯度求解目标函数的方法如下。

(1)设f:Rn→R为定义在欧氏空间上的目标函数，可以利用梯度下降法求解f的局部极小值，并给出迭代公式，如式(39)所示：

(39)

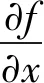
也可以通过牛顿法求解上述函数f的局部极小值

(40)

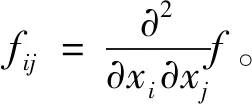
(2)设f:M→R为光滑函数，g为黎曼流形M上的黎曼度量。则有求解f的局部最小值的迭代公式为

θt+1=θt-μgradf(θt)

(41)

式(41)中：θt为第t次迭代统计量；gradf(θt)=g-1f(θt)表示黎曼梯度；f(θt)表示f在θt处的欧氏梯度；μ表示迭代步长。

有一种广义哈密顿算法在一定条件下可以消除陷于局部极小现象，而且可以加快迭代的收敛速度。

2 信息几何的应用

2.1 在统计推断领域的应用

对于无偏估计的有效估计问题，信息几何理论发挥了重要的作用。Amari[2-3]证明对于指数分布族，关于参数θ的对偶参数η，C-R(Cramer-Rao)不等式达到下界，即参数估计是有效的。而对于一般情形，通过引入辅助子流形和α曲率获得高阶渐进估计结果。

众所周知，Jeffreys先验在统计推断中起着重要的作用。Takeuchi与Amari利用信息几何推广了Jeffreys先验。引入了一个单参数先验分布族——α平行先验，当α=0时，与Jeffreys先验一致。进一步，利用α平行先验分析了各种估计量的渐近行为，如投影Bayes估计量和最小描述长度(MDL)估计量。虽然Jeffreys先验总是存在的，但α=0的α平行先验的存在并不总是有保证的，因此考虑了α平行先验的存在条件[17-18]。

2.2 在神经网络领域的应用

玻尔兹曼机是一个随机神经元网络。所有具有固定拓扑结构的玻尔兹曼机的集合形成一个高维的几何流形，其中可调节的突触连接重量起着指定网络的坐标系。例如，学习轨迹就是流形中的一条曲线。利用新的信息几何理论，在玻尔兹曼神经网络流形上建立了一个自然不变的黎曼度量和一对对偶仿射连接。从随机和统计的角度阐明了几何结构的含义。这导致了玻尔兹曼机器学习规则的自然修改[19-20]。

利用神经网络的随机模型，可以有效地实现由噪声污染实例给出的输入输出关系。当模型网络中包含有隐藏元时，基于随机模型从观测或指定的输入输出数据中估计隐藏变量是有用的。迄今为止，已有两种算法，EM(experctation maxization)算法和KL(Kullback-Leibler)算法被提出用于此目的。EM算法是利用条件期望的迭代统计方法，KL算法是由信息几何给出的几何算法。KL算法迭代最小化了神经网络流形中的K L散度。这两种算法在大多数情况下是等价的。利用信息几何可以给出研究神经网络随机模型的统一信息几何框架[21]。

人工神经网络(ANNs)被广泛应用于低层次神经活动和高层次认知功能的建模，统计推断为训练和评价训练人工神经网络的性能提供了一种客观的学习算法。文献[22]讨论了基于传统统计方法或贝叶斯方法的模型选择方法对过拟合问题的求解，综述了有监督和无监督学习算法在人工神经网络中的应用。指出了利用有监督学习训练多层神经网络相当于非线性回归。利用bagging和arching的方法形成一个新的具有改进性能的预测器，自组织的全局目标函数所导出的无监督学习算法被导出。

2.3 在控制理论领域的应用

当系统输入带有白噪声时，一个线性系统和一个非线性系统可以通过系统输出的概率分布来识别。这给出了概率分布族与系统之间的一一对应关系。所以系统流形的几何结构能通过信息几何进行研究[23]。设计一个随机控制系统，使得系统的输出与事先指定的目标尽可能接近。其中利用了KL散度充当两个流形之间的距离，黎曼梯度充当了求解目标函数最小值的最速下降方向[24-30]。

利用信息几何的方法研究稳定的时不变状态反馈系统的几何结构，从工程角度具有重要意义。把所有稳定状态反馈增益集参数化，并在稳定矩阵集中使用稳定状态反馈系统集的几何结构。所得结果不仅为参数化设计状态反馈增益提供了基本的指导，而且为分析线性稳定系统的结构提供了一种新的方法[31-34]。

2.4 在信号处理领域的应用

信号处理在军、民两个方面都具有十分重要的意义。无线通信、环境监测与预报、目标检测与跟踪等领域都需要高质量的信号处理结果。传统的信号处理建立在欧氏空间中，以傅里叶变换等为基础，进行信号的采样、恢复等。引入信息几何，利用黎曼度量与非欧氏距离，可以进一步精确地处理随机的复杂信号，为各种应用提供理论依据[35-38]。

传统的多普勒和阵列信号处理方法已经达到了极限。文献[6,39-41]结合矩阵信息几何，利用雷达数据协方差矩阵包含传感器信号的全部信息，提出了新的改进方法。利用信息几何研究雷达协方差矩阵的统计信息(在C-R界中使用Fisher信息矩阵的平均值)，建立一个稳健距离，称为Jensen、Siegel或Bruhat-Tits度量。在李群和Jordan代数框架下发展起来的“对称锥”上的几何为计算矩阵几何平均值提供了新的算法，可用于“矩阵CFAR(constant false alarm rate)”。这种创新的方法避免了在脉冲很少的情况下通过滤波器组或FFT(fast Fourier transform)进行多普勒处理的经典缺点。

文献[42-43]提出了一种基于黎曼距离定义的相异测度的K近邻脑电信号分类算法。利用功率谱密度矩阵流形上的曲线来表征脑电信号。通过给流形上赋予黎曼度量，得到了流形上两点之间的黎曼距离。在此基础上，定义了相异性度量。为了更好地分类相似性和不同的脑电信号集，得到了最优加权黎曼距离，目的是使不同类别的信号尽可能地分离，而同一类别的信号更紧凑。由此给出了算法设计的动机和验证方法。实验结果表明，与采用常用KL相异测度的K近邻脑电信号分类算法相比，该方法具有更好的性能。其核心的创新点是利用纤维丛的思想以及等距的性质，给出了对称正定矩阵流形上连接任意两点的测地距离的显式表达式。

2.5 在图像处理领域的应用

信息几何有效地应用于图像配准。例如在正定对称矩阵流形上建立一个仿射不变黎曼度量的理论框架，将该框架应用于扩散张量图像的处理，取得了很好的效果。结果表明，由于度量的仿射不变性，该框架有助于提取低层特征[44]。通过在正定对称矩阵流形上构造指数映射，使得流形成为一个平坦的李群，引入对数欧氏距离使得计算的复杂性得以降低[45]。利用正定矩阵流形的半监督距离度量学习，用于分类和图像检索以及多传感器估计融合[46-47]。

文献[48]考虑了以黎曼度量为基本结构的有限维流形。基于此度量提供了一个新的证据来证明黎曼质量中心和原始的梯度下降算法并进行有效的计算，提出了基于已知分布的均值和协方差的熵最大化的正态法则的概念。

分类和检索的准确性在很大程度上取决于用于计算样本之间相似度的度量。为了保持几何结构，将对称正定流形引入度量学习问题。文献[49]将内在度量学习问题推广到半定情形，从而更好地描述了各种分类任务的数据分布。数值结果表明，该方法能显著改善数据分布的描述，从而提高图像分类任务的性能。

2.6 在机器学习等领域的应用

统计机器学习处理随机情况并从样本中提取必要的信息。对于图模型，信念传播算法有效地利用了指数投影和混合投影。另一个应用是分析弱学习者组合的助推方法。可以用保角变换的几何思想来改进核支持向量机领域中的函数[50-53]。最近，最优传输理论与信息几何紧密结合，为信息几何的理论与应用带来了新鲜血液[54-56]。

度量在描述样本之间相似性方面起着关键作用。适当的数据度量可以很好地反映数据的分布，并进一步提高学习任务的效率。文献[57]利用几何方法提出了由局部到整体的半监督学习框架；文献[58]利用信息几何方法，探索了输入数据空间和输出嵌入空间中的几何，寻求流形学习的高维数据的低维表示[58]；文献[59]介绍了信息几何在机器学习、优化和统计推断等领域的应用。在统计流形上引入散度函数、黎曼几何结构、广义毕达哥拉斯定理以及相关的投影定理，为各种近似和优化问题提供了有效的方法。

3 结论与展望

随着人工智能、大数据应用的不断深入，复杂信息的处理与有效利用尤为重要。在传统的欧氏框架下，信息的处理遇到了困难，往往达不到精度。非欧框架下的信息几何方法为解决信息领域的瓶颈问题提供了可能。信息几何已经广泛地应用于信息科学的各个领域，但是还具有巨大的发展潜力。首先，信息几何的理论框架建立在比较苛刻条件的基础上，为保证Fisher信息矩阵的正定性，要求了正则性的条件，概率密度函数必须大于零，而很多情形下概率密度函数为零，这就使得很多随机现象无法被考虑。其次，随机的信息几何论框架几何不涉及拓扑性质，这就无法像研究黎曼几何那样，建立整体的信息几何框架。再次，既然带有Fisher信息的统计流形是黎曼流形，曲率就应该发挥刻画流形复杂度的核心作用[60-61]。最后，深刻的数学诸如代数拓扑、纤维丛等理论应该参入信息几何的框架中，形成更加完善的信息几何理论框架，扩展其应用范围，解决信息领域的瓶颈问题。

期望信息几何能够解决如下的问题。

(1)大数据的非线性降维。高维数据的降维对降低问题的复杂性，特别是可视化问题具有重要的意义。为了克服线性降维有时精度差的缺点，人们发展了流形学习这一非线性学习方法[62-63]。但是现有的流形学习方法也存在不足，无法做到精确的非线性降维。其原因在于，这些方法只是利用局部欧氏距离来代替真正的测地距离，即数据空间的几何性质并没有充分利用。如何充分利用数据空间的几何与拓扑性质，给出统一、精确的非线性降维方法是一个极具挑战的课题。

(2)深度学习。以AlphaGo为代表，深度学习展现出了惊人的应用前景。为了解决深层神经网络学习中收敛速度慢、梯度消失与梯度爆炸等问题，人们采取诸如卷积神经网络等方法来降低各层神经元之间的连接权值的数量，或者选择不同的激活函数等手段。但是这些方法都是有条件的情况下解决上述问题，同时会产生新的“副作用”。尽管在波尔兹曼机上可以把连接权值限制在流形上，进行几何刻画，但这也仅限于对波尔兹曼机这类随机神经网络。因此如何利用几何等方法，给出高效、统一的深度学习方法具有重要意义。

(3)人工智能的可解释性。依据深度强化学习算法的AlphaGo所向披靡，多位顶级围棋手只能投子认输。而然，AlphaGo的“妙手”是如何下出来的，人们并不清楚。如何给出可解释性的满意解答，对人工智能的发展至关重要。贝叶斯理论为解决因果推理提供了工具，但是在目前框架下的贝叶斯理论还不能给出令人满意的可解性解答。期望在非欧框架下，利用贝叶斯理论给出问题的解决方法。