TANG Rui，CHEN Long,2

(1． School of Mathematics，Sichuan University，Chengdu 610064，China; 2． School of Mathematics and Computer Science，Panzhihua University，Panzhihua 617000，China)

Abstract: This paper aims at the calculation of the fourth power mean of the generalized three-term exponential sums modulo p，an odd prime． By using some properties of the classical Gaussian sums and characteristical sums，we give some exact formulae and asymptotic formulae for it．

Keywords: Generalized three-term exponential sum; Characteristical sum; Fourth power mean; Asymptotic formula

1 Introduction

Letq≥3 be an integer. For any integermandn,the two-term exponential sumG(k,h,m,n;q) is defined as

where as usual,e(y)=e2πiy,kandnare positive integers withk>h.This sum plays an essential role in the research of analytic number theory. Plenty of classical problems are closely related to it. Whenk=pis an odd prime,it is closely related to Fourier analysis on finite fields. Many researchers had researched the properties ofG(k,h,m,n;q) and obtained many interesting results[1-11]. For instance,Zhang and Zhang[2]proved that for any odd primepwith (p,n)=1,we have the identity

They[4]also obtained that

In this paper,we mainly consider the computational problem of the fourth power mean of the generalized three-term exponential sum and Kloosterman sum

(1)

wherekis a positive integer,pis an odd prime. The main tool is some properties of the Gauss sum to compute (1) for gcd(k,p-1)=1,2,3,4 whenk=3,4 and give the exact calculating formulae and asymptotic formula when gcd(k,p-1) be an odd prime. We will prove the following results

Theorem1.1Letpbe an odd prime with gcd (n,p-1)=1 . Then

p(p-1)2(2p-3).

Theorem1.2Letpbe an odd prime withgcd(n,p-1)=2. Then

p(p-1)(2p2-7p+8).

Theorem1.3Letpbe an odd prime with gcd(n,p-1)=3,integerrwithr3≡1(modp) andr≢1(modp). Then we have the following identity

p(p-1)(2p2-5p+15)-4p(p-1)τ(χ2)·

Theorem1.4Letpbe an odd prime with gcd(n,p-1)=4 and integerrwithr2≡-1(modp). Then we have the following identity

p(p-1)(2p2-7p+24)-2p(p-1)·

2 Preliminaries

At first,we introduce some properties of the Gauss sum modulop. Letχbe a character defined modulop,χ0is the principal character modulop,then

By the orthogonality relations for Dirichlet characters,we have

The Gauss sum of a Dirichlet character modulopis

Letχbe a primitive character modp,we have

χ(n-1)τ(χ).

Ifχis a real primitive character modp,then

Ifχis an-th character modp,then for any integermwith (m,p)=1 we have

Particularly,

Letaandbbe two integer and gcd(2a,N)=1,we have

Lemma2.1Letpbe a prime with 3|(p-1),integerrwithr3≡1(modp) andr≢1(modp),then

ProofAccording to the properties of the reduced residue system modp,ifbpass through a reduced residue system modp,thena=br2anda=a-2-1also pass through a reduced residue system modp. We obtain

This proves the lemma.

Lemma2.2Letpbe a prime with 3|(p-1),integerrwithr3≡1(modp) andr≢1(modp),then

ProofAccording to the properties of the reduced residue system modp,ifcpass through a reduced residue system modp,thencralso pass through a reduced residue system modpandr2+r+1≡0(modp). Thus we obtain

(2)

From the properties of Gauss sum we know that

From the properties of the reduced residue system modp,we have

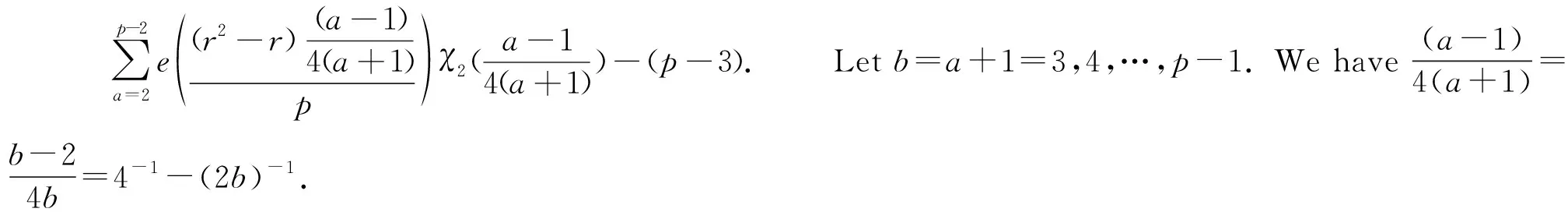
χ2(4-1-2-1b-1)-(p-3)=τ(χ2)·

the thirth part and fourth parts of (2).Then,from the properties of Gauss sum,we get

This proves the lemma.

Lemma2.3Letpbe an odd prime with 4|(p-1),integerrwithr2≡-1(modp),then

ProofAccording to the properties of the reduced residue system modp,ifbpass through a reduced residue system modp,thena=b-1also pass through a reduced residue system modp. From the properties of Gauss sum we know that

Then,from the orthogonality of the characters modp,we obtain that

Lemma2.4Letpbe an odd prime with 4|(p-1),integerrwithr2≡-1(modp),then we have

ProofAccording to the properties of the reduced residue system modp,ifapass through a reduced residue system modp,thenb=4-1a-1also pass through a reduced residue system modp.From the properties of Guass sums and reduced system,we obtain

τ(χ2)χ2(-2(a2-1))-(p-5)=

The proof is end.

ProofofTheorem1.1By the orthogonality of characters modp,we obtain

p(p-1)2(2p-3).

This finishes the proof of Theorem 1.1.

ProofofTheorem1.2By the orthogonality of characters modp,we obtain

p(p-1)(2p2-7p+8).

This finishes the proof of Theorem 1.2.

ProofofTheorem1.3By the orthogonality of characters modp,we obtain

(3)

According to Lemma 2.2,we can calculate the second part and third part of (3) as follows.

According to Lemma 2.3,we focus on the fourth part of (3),which is equal to

Thus

This finishes the proof of Theorem 1.3.

ProofofTheorem1.4Let 1,r,r3,-1 be different root ofx4≡1(modp). By the orthogonality of characters modp,we obtain

(4)

According to Lemma 2.3,we can calculate the sum of the second and the third part of equation (4) as follows.

2p(p-1)(p+1)-2p(p-1)

According to Lemma 2.4,we can obtain the fourth part of equation (4) as follows.

Hence

This finishes the proof of Theorem 1.4.

ProofofTheorem1.5Letdbe the smallest positive integer such thatrd≡1(modp). By the orthogonality of characters modp,we obtain

(5)

Then we focus on the second part of (5). By the method similar to Lemma 2.3,we obtain

and

The rest of the proof is similar to the proofs of Theorem 1.1～Theorem 1.4,except the proof of the last part of (5). By orthogonality of characters modp,we know

(6)

In what follows we calculate the second part of (6) the rest parts can be done in the same way. From the properties of Gauss sum and residues system,we know the second part is

where

Hence,the last part of (4) is

where

Thus

where

(d2+2d+2)p2-(d2+2d-1)p.

This finishes the proof.

p(p-1)2(2p-3).

Corollary3.2Letpis a prime with 3|(p-1),integerrwithr3≡1(modp) andr≢1(modp),then

p(p-1)(2p2-5p+15)-4p(p-1)τ(χ2)·

Corollary3.3For any primep,we have the following asymptotic formula

p(p-1)(2p2-7p+8).

Corollary3.5Letpis a prime with 4|(p-1),integerrwithr2≡-1(modp),then

p(p-1)(2p2-7p+24)-2p(p-1)·

Corollary3.6For any primep,such that the following asymptotic formula

On the other hard,we can only obtain the asymptotic formula for Theorem 1.5.

ConjectureWe leave the following conjecture ：letpbe an odd prime andgcd(n,p-1)=dis a fixed positive integer. If 2|d,then we have the asymptotic formula