陈 芬，谢绍龙，柏仕坤

(1.重庆师范大学 数学科学学院，重庆 401331;2.玉溪师范学院 商学院，云南 玉溪 653100)

1 问题提出

本文主要研究如下的二阶Dirichlet边值问题

(1.1)

其中非线性项f满足条件：(H1)f∈C([0,1]×R,R),R=(-∞,+∞).

众所周知，问题(1.1)及其相关问题来源于应用数学与数学物理的诸多领域，参见文献[1]～[10]及其所附参考文献.在文献[1]中，作者运用锥上的不动点定理研究二阶Dirichlet边值问题正解的存在性:

其中f∈C([0,1]×[0,∞),[0,∞))满足以下条件：

(A1)f0=0,f∞=∞

(A2)f0=∞,f∞=0,

(1.2)

其中

文献[2]～[4]运用条件(A1)(A2)获得了问题(1.1)的正解.文献[5]则把这两个条件分别改进为

f0<λ1,f∞>λ1;f0>λ1,f∞<λ1,

其中λ1=π2是相应线性算子的第一特征值，类似的结论可参见文献[6].

然而我们注意到，上述文献考虑的模型的非线性项大多数是非负连续的，且被称做最优条件的(A1)′～(A2)′仅仅做到了与第一特征值有关的结果.而本文所讨论的非线性项可以变号，且与相关算子的所有特征值均相关.从而本文的结论可以看作是上述文献的推广和改进.

2 主要结论

我们首先将问题(1.1)转化为与其等价的积分方程，并给出相应的Green函数.根据求导规则可得

(2.1)

其中ci(i=1,2)是常数.对(2.1)式两边关于t求两次导数可得

从而(1.1)式中第一个方程满足.将(1.1)式中的边值条件代入(2.1)式,可计算出常数c1,c2:

代入(2.1)得

其中

(2.2)

此时分段函数G称为问题(1.1)的Green函数.为得到本文的主要结论，我们需考虑如下的特征值问题：

(2.3)

其中参数λ称为问题(2.3)的特征值，而对应的函数u称为特征向量.可运用常微分方程的知识解出该特征值和特征向量.当λ≤0时问题(2.3)仅有0解，所以仅需考虑λ>0的情况.此时(2.3)的解可表示为:

注意到问题(1.1)转化的积分方程的表现形式，同理可得特征值问题(2.3)的积分方程：

再将计算出来的特征值和特征向量代入，我们有

(2.4)

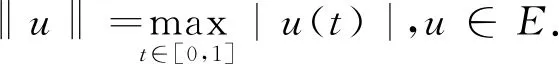
为了证明本文的结论，我们给出以下的不动点定理：

以下是本文的主要结论及其证明.

(H3)f(t,0)不恒等于0,t∈[0,1]

定理2.2 若(H1)～(H3)满足，则(1.1)至少有一个非平凡解.

以下首先证明1不是T的特征值.反证法，则存在u0∈E{0}是1对应的特征向量，从而可得

(2.5)

情形1 若ω=0,则u0(t)≡0,t∈[0,1],与特征向量非平凡性的要求矛盾.

情形2ω≠0则由(2.5)可得

(2.6)

此时若ω>0,则(2.6)的解可表示为

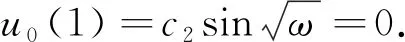
若ω<0,则(2.6)的解可表示为

从而由边界条件u0(t)=u0(1)=0可得

计算此方程可得c1=c2=0,从而(2.6)只有零解, 与特征向量非平凡性的要求矛盾.

以上两个矛盾表明1不是T的特征值.

从而对任意的ε>0, 存在M>0使得

|f(t,u)-ωu|≤ε|u|,|u|≥M,t∈[0,1].

此时我们有

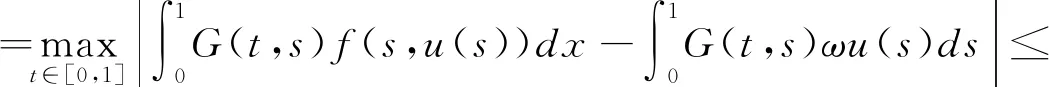
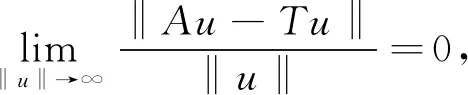
再由(H3)知0不是A的不动点,从而A至少有一个非平凡不动点，即(1.1)至少有一个非平凡解. 证毕.