CENTRAL LIMIT THEOREM AND MODERATE DEVIATIONS FOR A CLASS OF SEMILINEAR STOCHASTIC PARTIAL DIFFERENTIAL EQUATIONS*
2020-11-14ShulanHU胡淑兰
Shulan HU (胡淑兰)
School of Statistics and Mathematics, Zhongnan University of Economics and Law,Wuhan 430073, China
E-mail :hu shulan@zuel.edu.cn
Ruinan LI (李瑞囡)
School of Statistics and Information, Shanghai University of International Business and Economics,Shanghai 201620, China
E-mail :ruinanli@amss.ac.cn
Xinyu WANG (王新宇)†
School of Mathematics and Statistics, Huazhong University of Science and Technology,Wuhan 430074, China
E-mail :wang xin yu@hust.edu.cn
Abstract In this paper we prove a central limit theorem and a moderate deviation principle for a class of semilinear stochastic partial differential equations, which contain the stochastic Burgers’ equation and the stochastic reaction-diffusion equation. The weak convergence method plays an important role.
Key words stochastic Burgers’ equation; stochastic reaction-diffusion equation; large deviations; moderate deviations
1 Introduction
For any ε > 0, consider the semilinear stochastic partial differential equation (SPDE for short)
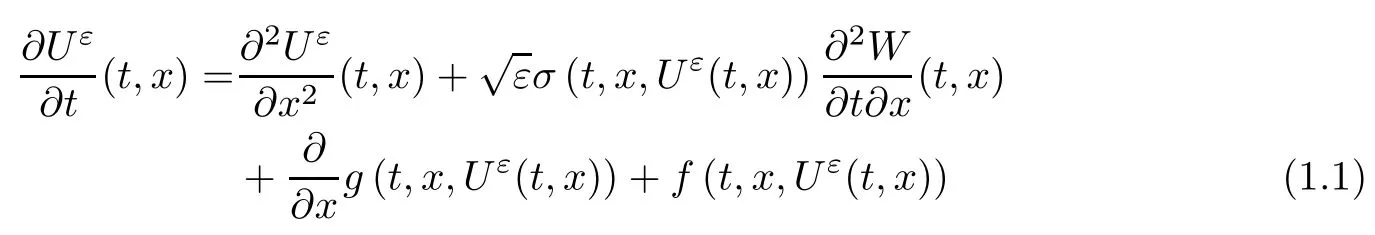
for all (t,x) ∈ [0,T]× [0,1], with Dirichlet boundary conditions (Uε(t,0) = Uε(t,1) = 0) and initial condition Uε(0,x) = η(x) ∈ Lp([0,1]),p ≥ 2; W denotes the Brownian sheet defined on a probability space (Ω,F,{Ft}t≥0,P); the coefficients f =f(t,x,r),g =g(t,x,r),σ = σ(t,x,r)are Borel functions of (t,x,r) ∈ R+× [0,1]× R (see Section 2 for details). This family of semilinear equations contain both the stochastic Burgers’equation and the stochastic reactiondiffusion equation; see Gyngy [15]for details.
Intuitively, as the parameter ε tends to zero, the solutions Uεof (1.1) will tend to the solution of

for all (t,x)∈ [0,T]× [0,1], with the Dirichlet boundary conditions and initial condition η(x).
It is always interesting to investigate deviations of Uεfrom the deterministic solution U0as ε decreases to 0; that is, the asymptotic behavior of the trajectory

where λ(ε) is some deviation scale which strongly influences the asymptotic behavior of Xε.
(2) If λ(ε)is identically equal to 1,we are in the domain of the central limit theorem(CLT for short). We will show thatconverges to a random field as ε ↓ 0.
(3) When the deviation scale satisfies

We are dealing with the moderate deviations (see [7, 13]). Throughout this paper, we assume that (1.3) is in place.
The moderate deviation principle (MDP for short) enables us to refine the estimates obtained through the central limit theorem. It provides the asymptotic behavior forwhile the CLT gives asymptotic bounds for
Like large deviations, moderate deviations arise quite naturally in the theory of statistical inference. The MDP can provide us with the rate of convergence and a useful method for constructing asymptotic confidence intervals; refer to the recent works [10, 11, 14]and the references therein. Usually, the quadratic form of the MDP’s rate function allows for explicit minimization and, in particular, it allows one to obtain an asymptotic evaluation for the exit time;see[18]. Quite recently,the study of the MDP estimates for stochastic(partial)differential equations was carried out as well; see [4, 8, 12, 17, 19, 21, 22]etc.. In particular,Belfadli et al.[1]proved an MDP for the law of a stochastic Burgers’ equation and established some useful estimates toward a CLT.
In this paper, we shall study the problems of the CLT and the MDP for the semilinear SPDE (1.1)which contains a stochastic Burgers’equation and the stochastic reaction-diffusion equation. We generalize the moderate deviation result in[1]and prove the central limit theorem.
The rest of this paper is organized as follows: in Section 2, we give the framework of the the semilinear SPDEs, and state the main results of the paper. In Section 3, we prove some convergence results. Section 4 is devoted to the proof of the central limit theorem. In Section 5, we prove the moderate deviation principle by using the weak convergence method.
Throughout the paper,C(p) is a positive constant depending on the parameter p, and C is a constant depending on no specific parameter (except T and the Lipschitz constants), whose value may be different from line to line by convention.
2 Framework and Main Results
2.1 Framework
Let us give the framework taken from [9]and [15].
For any T > 0, assume that the coefficients f = f(t,x,r),g = g(t,x,r),σ = σ(t,x,r) in(1.1) are Borel functions of (t,x,r) ∈ [0,T]× [0,1]× R and that there exist positive constants K,L satisfying the following conditions:
(H1) for all (t,x,r)∈ [0,T]×[0,1]×R, it holds that
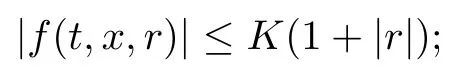
(H2) the function g is of the form g(t,x,r) = g1(t,x,r)+g2(t,r), where g1and g2are Borel functions satisfying that
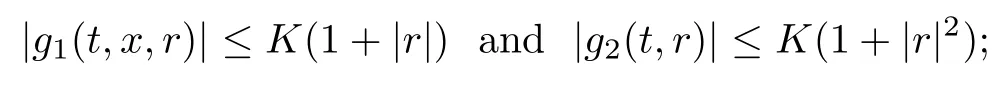
(H3) σ is bounded and for any (t,x,p,q)∈ [0,T]×[0,1]×R2,
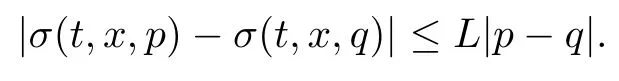
Furthermore, f and g are locally Lipschitz with a linearly growing Lipschitz constant, i.e.,

Definition 2.1(mild solution) A random field Uε= {Uε(t,x) : t ∈ [0,T],x ∈ [0,1]} is called a mild solution of (1.1) with initial condition η if Uε(t,x) is Ft-measurable, (t,x) →Uε(t,x) is continuous a.s., and
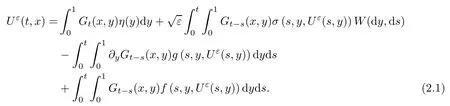
Here Gt(·,·) is the Green kernel associated with the heat operator ∂/∂t − ∂2/∂x2with the Dirichlet boundary conditions.
Foondun and Setayeshgar [9]proved the following result for the existence and uniqueness of the solution to eq.(1.1):
Theorem 2.1([9, Theorem 2.2]) Under conditions (H1)–(H3), for any η ∈ Lp([0,1]),p ≥2, there exists a measurable functional
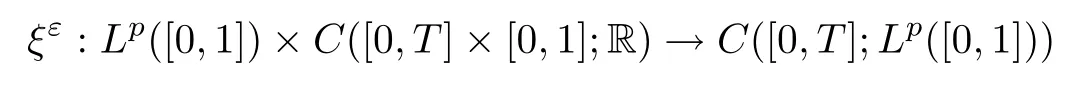
Furthermore,from the proof of[9,Theorem 2.2],we know thatis bounded in probability, i.e.,
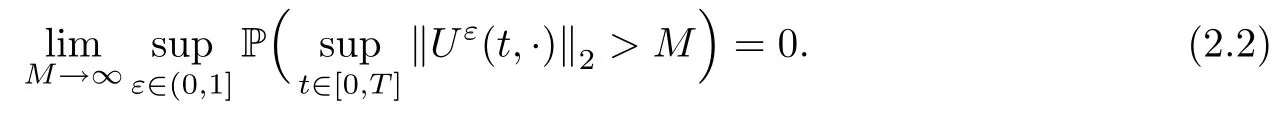
Particularly,taking ε=0 in(1.1),we know that the determinate equation(1.2)admits a unique solution U0∈C([0,T];L2([0,1])), given by

2.2 Main results
To study the CLT and the MDP, we furthermore suppose that
(H4) the coefficients f and g are differentiable with respect to the last variable, and the derivatives f′and g′are uniformly Lipschitz with respect to the last variable; more precisely,there exists a positive constant K′such that
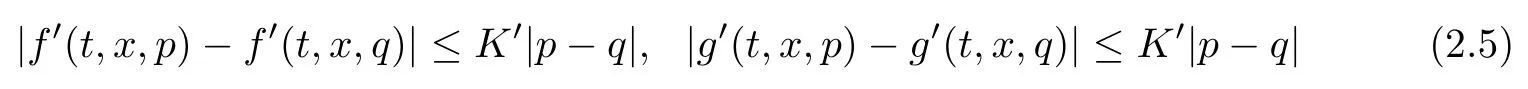
for all (t,x)∈ [0,T]× [0,1],p,q ∈ R.
Combined with the growth condition (H3), we conclude that

Our first main result is the following functional central limit theorem:
Theorem 2.2Under conditions (H1)–(H4), for any T > 0, the processconverges to a random field V in probability on C([0,T];L2([0,1])), determined by
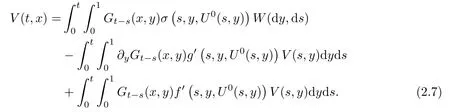
The Cameron-Martin space associated with the Brownian sheet {W(t,x);t ∈ [0,T], x ∈[0,1]} is given by
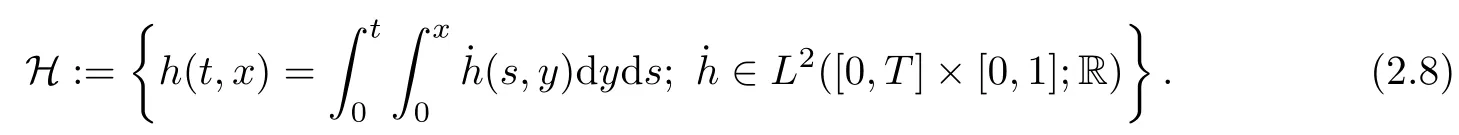
The space H is a Hilbert space with inner product

The Hilbert space H is endowed with the norm
In view of the assumption (1.3) and (2.5), by the LDP for SPDE (see [6]), one can obtain that V/λ(ε) obeys an LDP on C([0,T];L2([0,1])) with the speed λ2(ε) and with the good rate function
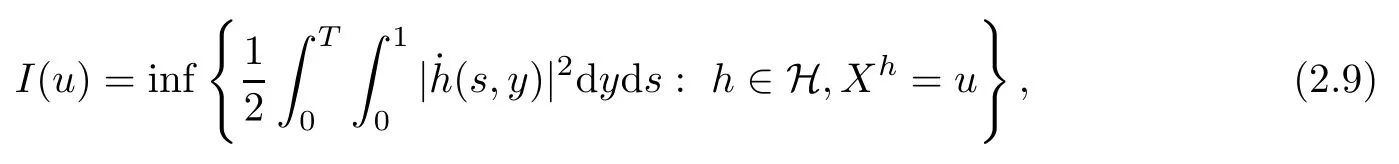
where the function Xhis the solution of the following deterministic partial differential equation:
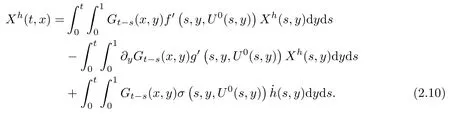
Our second main result reads as follows:
Theorem 2.3Under conditionsobeys an LDP on C([0,T];L2([0,1])) with the speed λ2(ε) and with the rate function I given by (2.9).
3 Some Preliminary Estimates
3.1 Some preliminary estimates
The following estimates of Green function G hold (see Cardon-Weber [6], Walsh [20],Gyngy [15]): there exist positive constants K,a,b,d such that for all x,y ∈ [0,1]and 0 ≤s where ρ is the Euclidean distance in [0,T]× [0,1]. For any v ∈ L∞([0,T];L1([0,1])),t ∈ [0,T],x ∈ [0,1], let J be a linear operator defined by Lemma 3.1([15, Lemma 3.1]) For any ρ ∈ [1,∞],q ∈ [1,ρ],K := 1+ 1/ρ − 1/q, it holds that J is a bounded linear operator from Lγ([0,T];Lq[0,1])into C([0,T];Lρ[0,1])for any γ >2K−1. Moreover,J satisfies the following inequalities: (1) For every t ∈ [0,T]and γ >2K−1, (2) For every 0< α This section is concerned with the convergence of Uεto U0as ε → 0. For any M >0, define the stopping time By (2.2), we know that Proposition 3.2Under conditions (H1)–(H3), there exists some constant C(M,L,σ,T)depending on M,L,σ,T such that ProofSince by (H3) and Cauchy-Schwarz’s inequality, we have that for any (t,x)∈ [0,T]× [0,1], Hence, applying Lemma 3.1 with ρ =2,q =1, and by Cauchy-Schwarz’s inequality, we have First taking the supremum of time over [0,t ∧ τM,ε], and then taking the expectation, by the definition of τM,εwe obtain that where we have used Fubini’s theorem in the last inequality. Putting (3.10), (3.12), (3.13) and (3.14) together, we have By Gronwall’s inequality (see [23]), we know that there exists a constant C(M,L,σ,T) such that The proof is complete. Proof of Theorem 2.2LetWe will prove that for any δ >0, Recall the stopping time defined by to prove (4.1) by (3.8), it is sufficient to prove that for any M >0 large enough, By the definition of Vεand V, we have By Taylor’s formula, there exists a random field ηεtaking values in (0,1) such that Since f′is Lipschitz continuous, we have If we frist take the supremum of s over[0,t∧τM,ε],and then take the expectation,by Proposition 3.2 we have By first taking the supremum of s over [0,t ∧ τM,ε], and then taking the expectation, we have Using (4.5) and (4.6), we have For the term A3, by first taking the supremum of time over [0,t ∧ τM,ε], and then taking the expectation, by Burkholder’s inequality for stochastic integrals against Brownian sheets(see [16]), the Lipschitz continuity of σ and Proposition 3.2, we have Putting (4.3) and (4.7)–(4.9) together, we have By Gronwall’s inequalities ([23, Theorem 1]), (2.4) and (2.6), we have which implies (4.2). The proof is complete. First, recall the definition of a large deviation principle (c.f.[7]). Let (Ω,F,P) be a probability space with an increasing family {Ft}0≤t≤Tof the sub-σ-fields of F satisfying the usual conditions. Let E be a Polish space with the Borel σ-field B(E). Definition 5.1A function I : E → [0,∞]is called a rate function on E, if for each M < ∞, the level set {x ∈ E : I(x) ≤ M} is a compact subset of E. A family of positive numbers {λ(ε)}ε>0is called a speed function if λ(ε)→ +∞ as ε → 0. Definition 5.2{Xε}is said to satisfy the large deviation principle on E with rate function I and with speed function {λ(ε)}ε>0, if the following two conditions hold: (a) (Upper bound) For each closed subset F of E, (b) (Lower bound) For each open subset G of E, Let A denote the class of real-valued{Ft}-predictable processes φ belonging to H a.s.,and let The set SNendowed with the weak topology is a Polish space. Define Recall the following result from Budhiraja et al. [5], which is based on certain variational representations for infinite dimensional Brownian motions ([2, 3]): Theorem 5.1([5, Theorem 7]) For any ε > 0, let Γεbe a measurable mapping from C([0,T]× [0,1];R) into E. Suppose that {Γε}ε>0satisfies that there exists a measurable map Γ0:C([0,T]×[0,1];R)−→ E such that (a) for any N <+∞ and family {hε}ε>0⊂ ANsatisfying that hεconverge in distribution as SN-valued random elements to h as ε → 0,converges in distribution to (b) for every N <+∞, the setis a compact subset of E.Then the family {Γε(W)}ε>0satisfies an LDP in E with the rate function I given by with the convention inf ∅ = ∞. The purpose of this part is to study the skeleton equation, which will be used in the weak convergence approach. Recall the skeleton equation defined in (2.10). Using the same strategy as that in the proof of the existence and uniqueness of the solution to eq.(1.1), we can state Proposition 5.2Under conditions (H1)–(H4), eq.(2.10) admits a unique solution in C([0,T];L2([0,1])) satisfying that For any h ∈H, set where Xhis the solution of (2.10). Theorem 5.3Under conditions (H1)–(H4), the mapping SN∋ h → Xh∈ C([0,T];L2([0,1])) is continuous with respect to the weak topology. ProofLet {h,(hn)n≥1} ⊂ SNsuch that for any g ∈ H, We need to prove that Notice that By Cauchy-Schwarz’s inequality, (2.4), (2.6) and (5.2), we have Similarly, we obtain that Since σ is bounded, for any fixed (t,x)∈ [0,T]×[0,1],the function Gt−s(x,y)σ(s,y,U0(s,y)):(s,y) ∈[0,t]×[0,1]→R belongs to L2([0,T]×[0,1];R). Asweakly in L2([0,T]×[0,1];R), it holds that For any 0 ≤ s ≤ t ≤ T, applying formulas (3.5) and (3.6), by the boundness of σ and Hlder’s inequality, we obtain that In particular, taking s=0, we obtain that Hence, by a generalized Gronwall lemma (eg. [23, Theorem 1]), we have which, together with (5.12), implies the desired estimate (5.5). The proof is complete. This equation admits the unique strong solution where Γεstands for the solution functional from C([0,T]× [0,1];R) into C([0,T];L2([0,1])). The following lemma is a direct consequence of Girsanov’s theorem (refer to [9, Theorem 3.2]): Lemma 5.4For every fixed N ∈ N, let h ∈ ANand Γεbe given by (5.14). Then Xε,h:= Γε(W + λ(ε)h)∈ C([0,T];L2([0,1])) solves the following equation: Furthermore, by a similar calculation to that of [19, Lemma 5.2], we know that Proposition 5.5Assume(H1)–(H4). For every fixed N ∈ N,let hε,h ∈ ANbe such that hεconverges in distribution to h as ε → 0. Then in C([0,T];L2([0,1])) as ε → 0, where Γεand Γ0are given by (5.14) and (5.3), respectively. ProofBy the Skorokhod representation theorem, there exists a probability basisand, on this basis, a sequence of independent Brownian sheetsand a family of F¯t-predictable processesbelonging totaking values on SN,such that the joint law of (hε,h,W) under P coincides with that ofunderand From now on, we drop the bars in the notation for the sake of simplicity. Notice that Term. Since σ is bounded, by Burkholder’s inequality for stochastic integrals against Brownian sheets (see [16]), we have By Taylor’s formula, there exists a random field ηε(s,y) taking values in (0,1) such that Since f′is Lipschitz continuous, we have Define the stopping time where M is some constant large enough. Taking the supremum of time over[0,t∧τM,ε],and then taking the expectation,we obtain that Putting (5.21) and (5.22) together, we have In a fashion similar to the proof of (5.23), we obtain the following estimate for: Using the same argument as that in the proof of (5.12), we obtain that By the Lipschitz continuity of σ, we know that By first taking the supremum of t over[0,T ∧τM,ε],and then taking the expectation,we obtain that According to (5.25)–(5.27), we have that Putting (5.18), (5.19),(5.23),(5.24)and(5.28)together,and by Gronwall’s inequality([23,Theorem 1]), we have By Chebychev’s inequality, we have Letting M →∞, by (5.16) we get the desired result (5.17). The proof is complete. We are now ready to prove our main result. Recall the mapping Γ0given by (5.3). For any u ∈C([0,T];L2([0,1])), let Proof of Theorem 2.3According to Theorem 5.1, we need to prove that the following two conditions are fulfilled: (a) the set {Xh;h ∈SN} is a compact set of C([0,T];L2([0,1])), where Xhis the solution of eq.(2.10); (b) for any family {hε}ε>0⊂ ANwhich converges in distribution as ε → 0 to h ∈ ANas SN-valued random variables, we have that as C([0,T];L2([0,1]))-valued random variables, where Xhdenotes the solution of eq.(2.10)corresponding to the SN-valued random variable h (instead of a deterministic function). Condition(a)follows from the continuity of the mapping SN∋ h → Xh∈ C([0,T];L2([0,1])),which was established in Theorem 5.3. The verification of condition(b)is given by Proposition 5.5. The proof is complete. AcknowledgementsWe would like to express our appreciation for R.Belfadli,L.Boulanba and M.Mellouk. They told us about their work on the stochastic Burgers’equation and pointed out a mistake in our paper.




3.2 The convergence of Uε


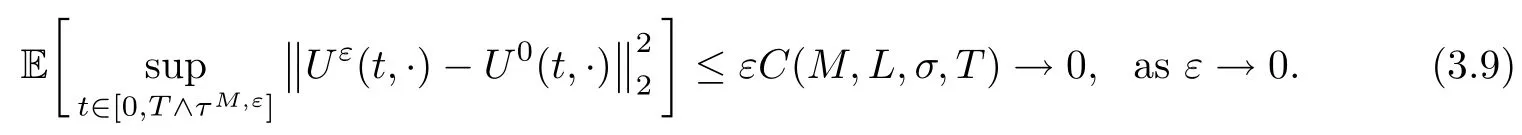

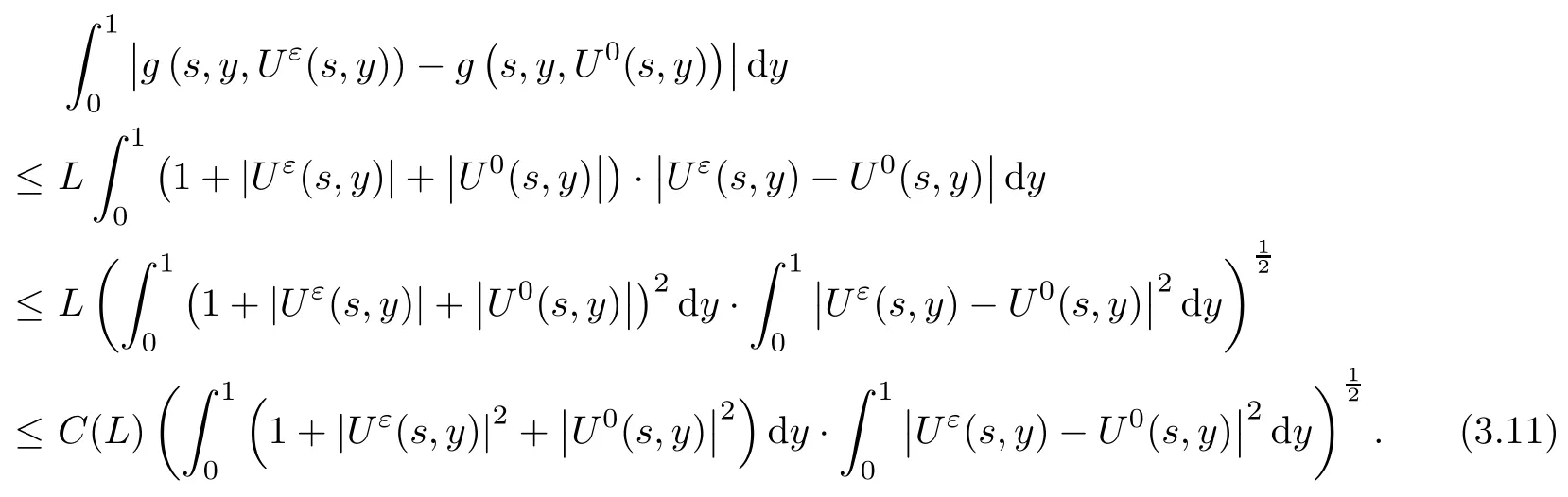


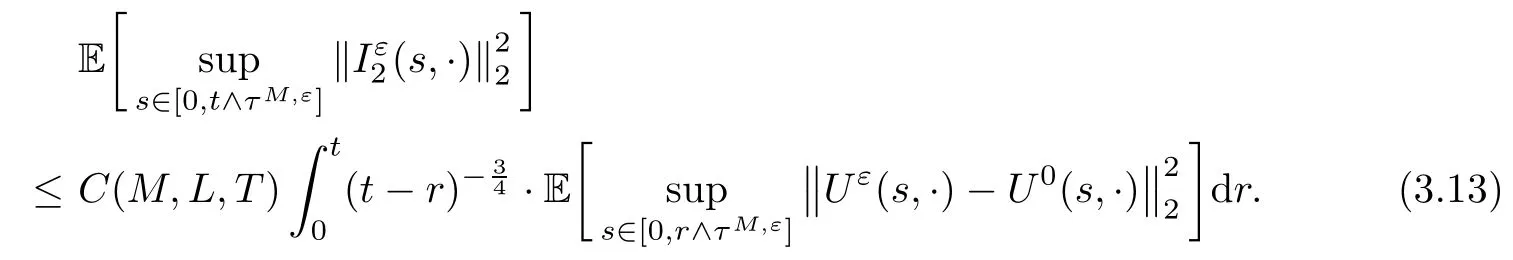
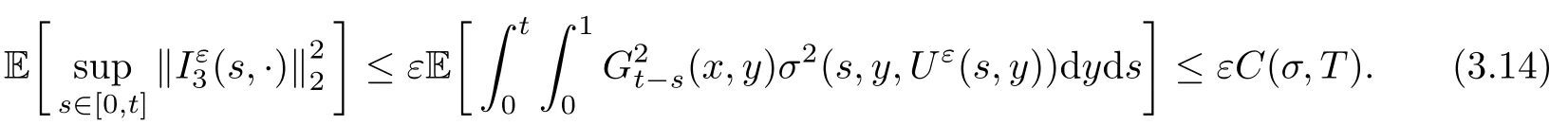
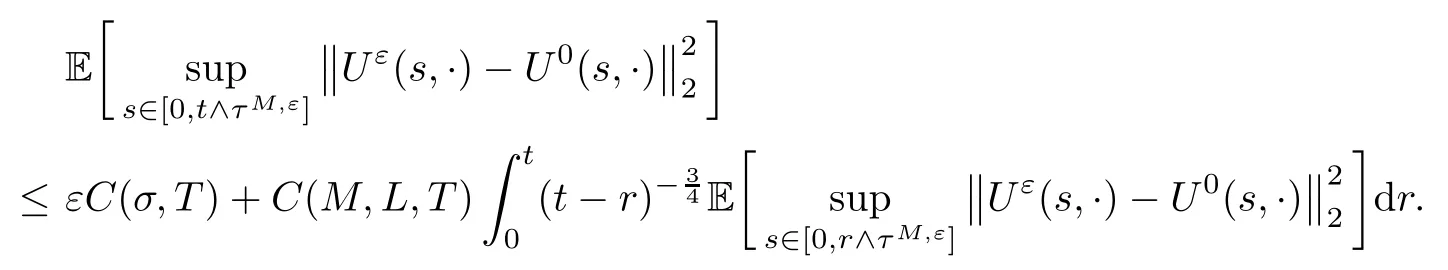
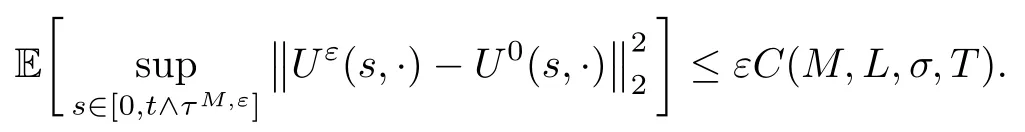
4 Proof of the Theorem 2.2

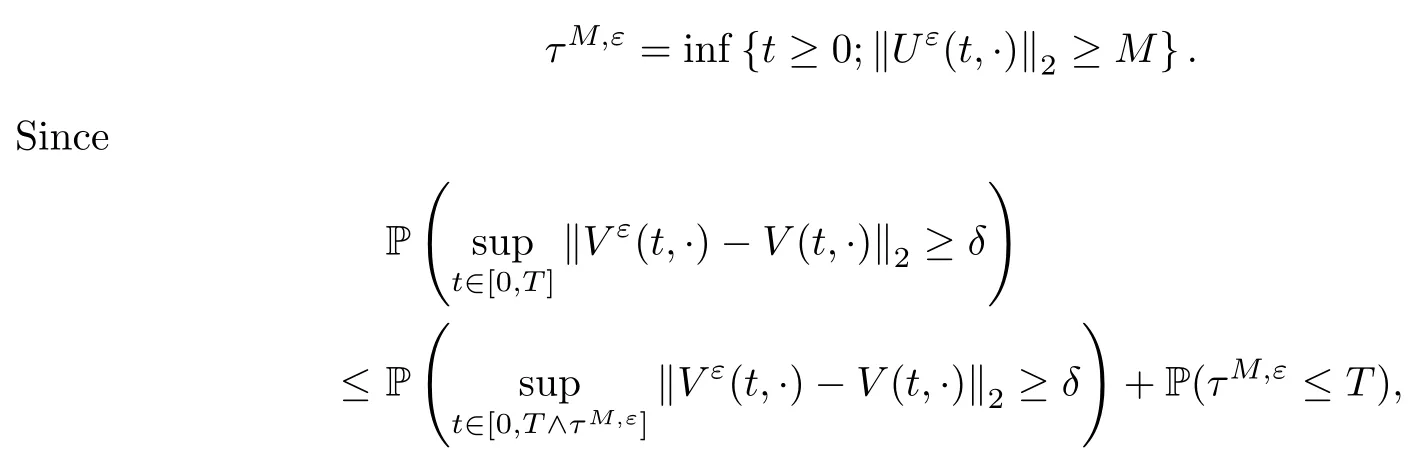

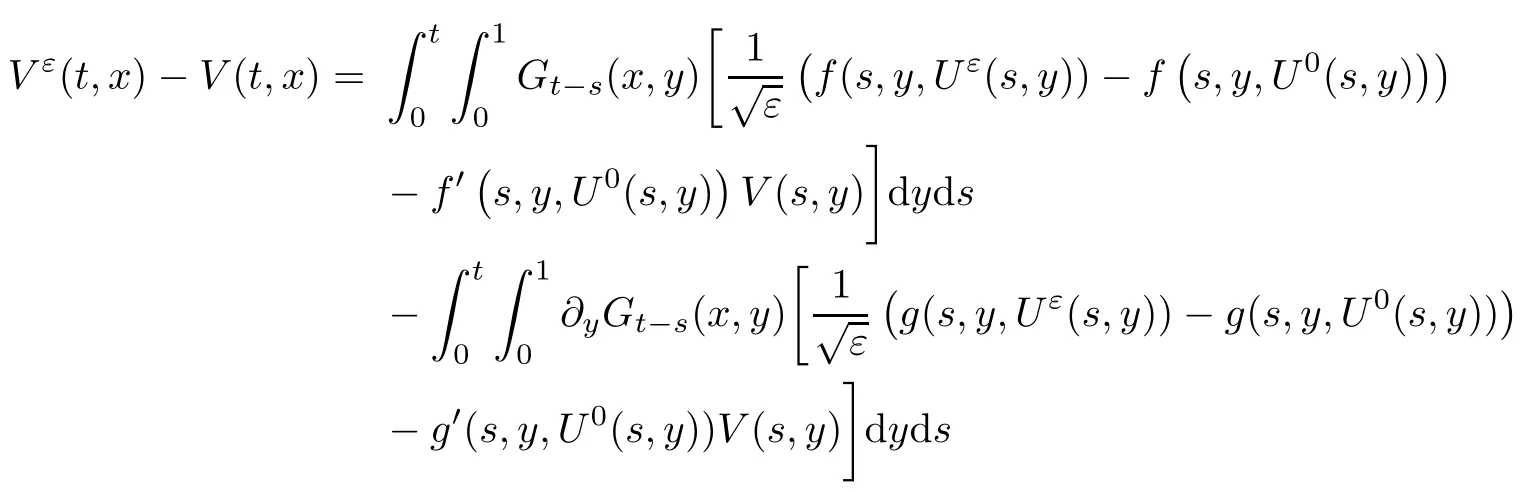




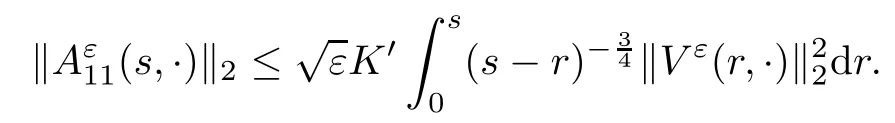



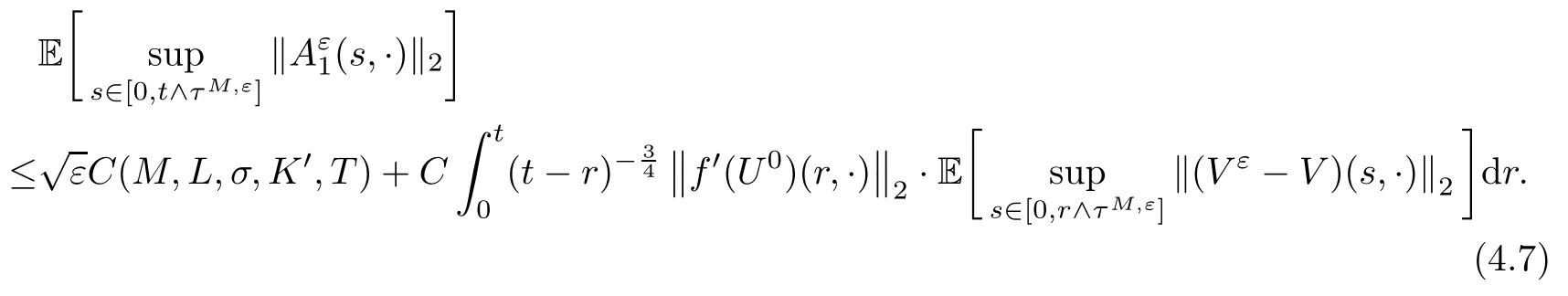

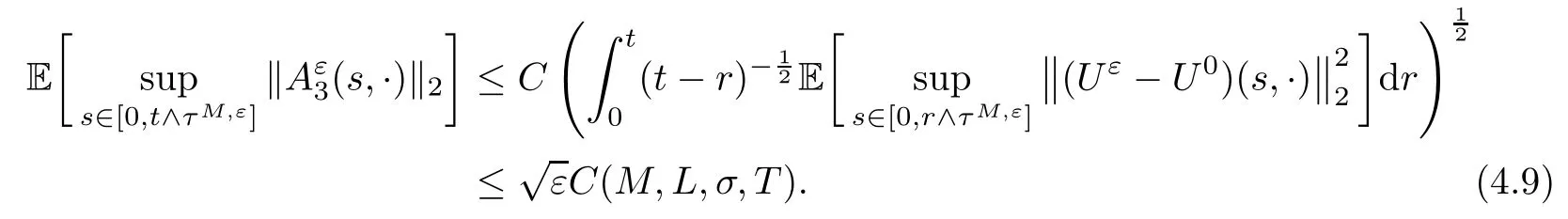
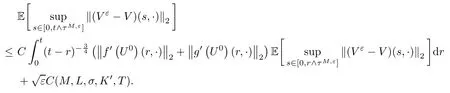
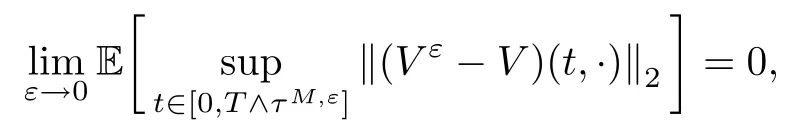
5 Proof of the Theorem 2.3
5.1 Weak convergence approach in LDP
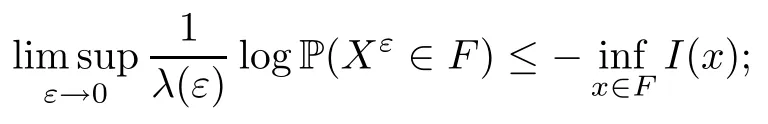
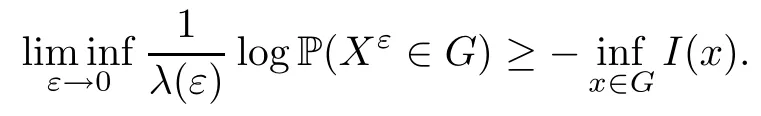
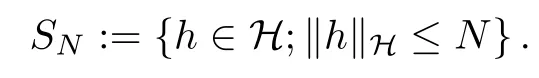
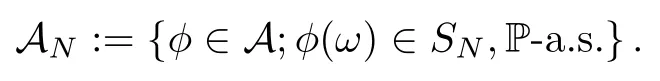
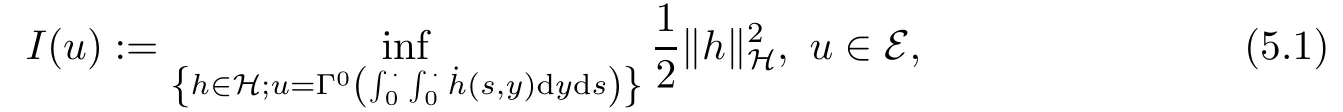
5.2 The skeleton equation



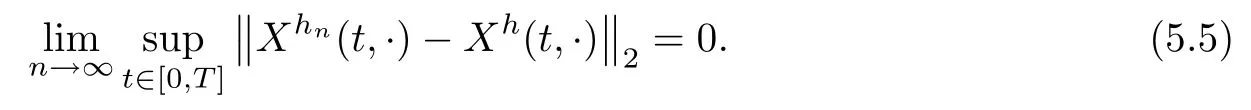
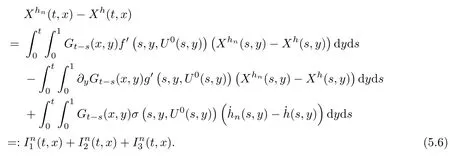
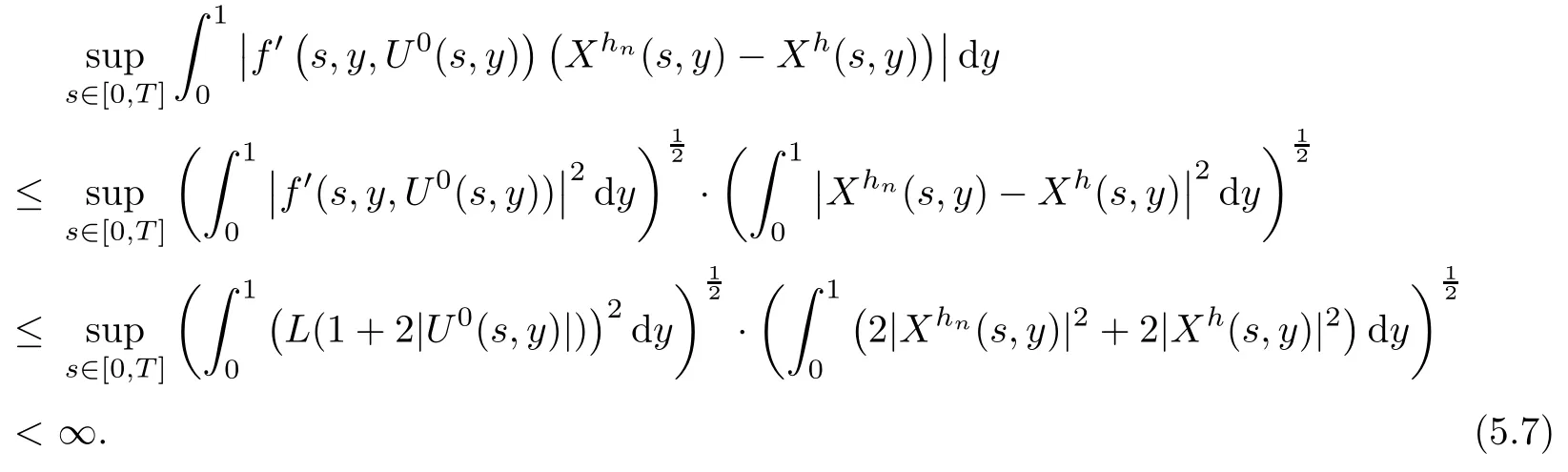

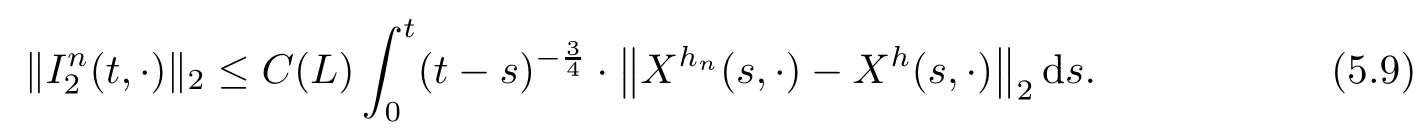
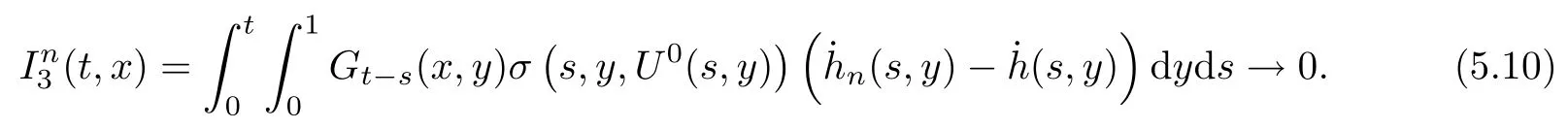



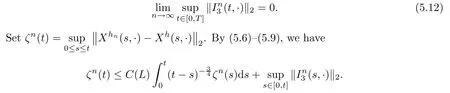
5.3 The controlled equation



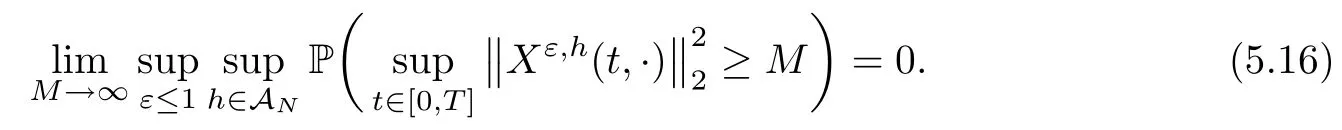


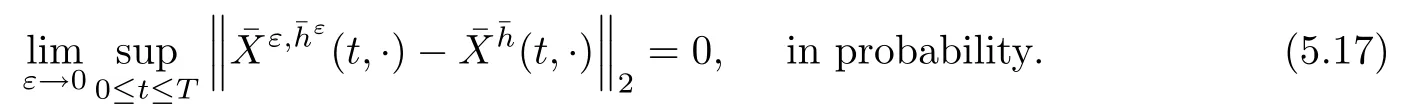
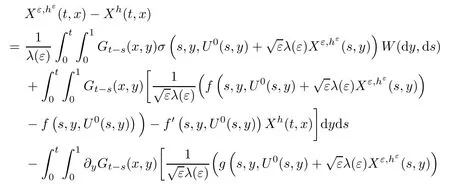
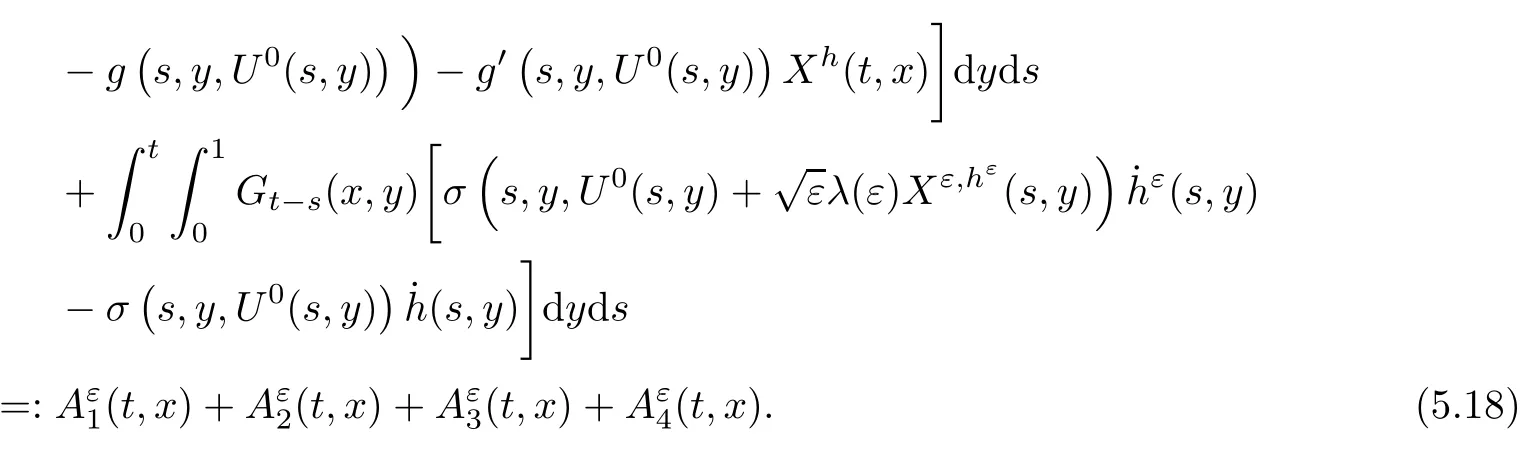
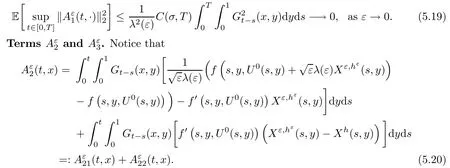
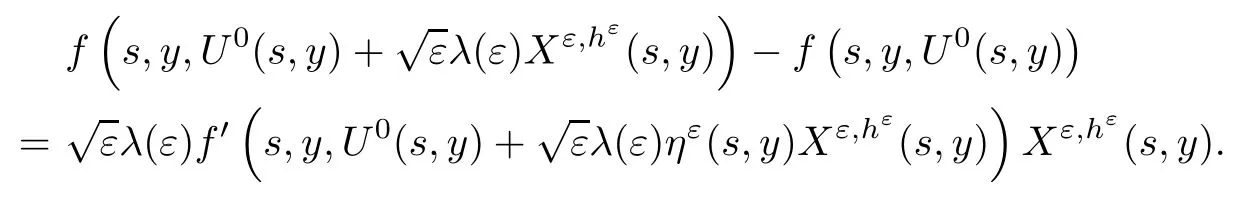



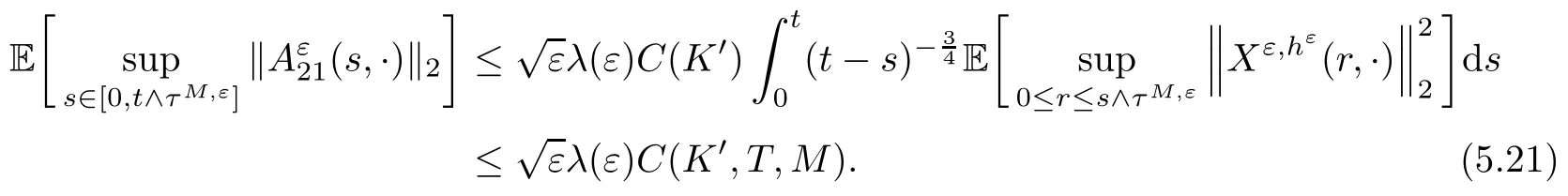

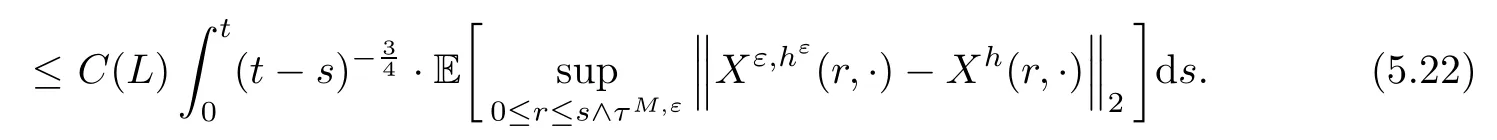
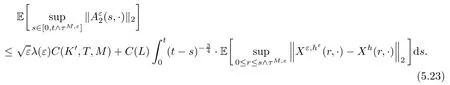


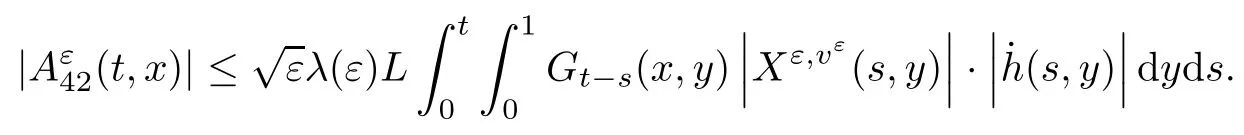
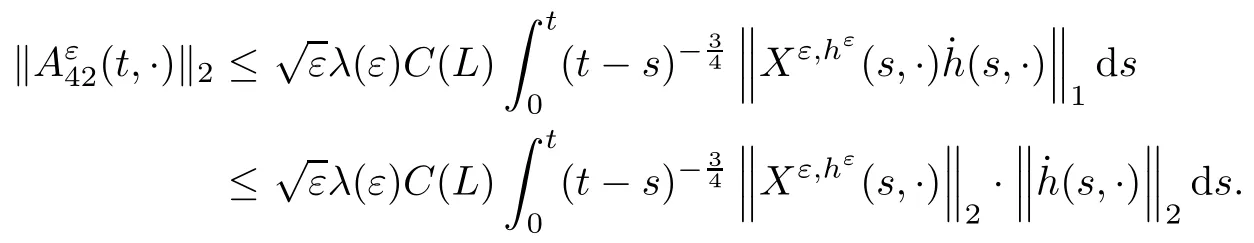
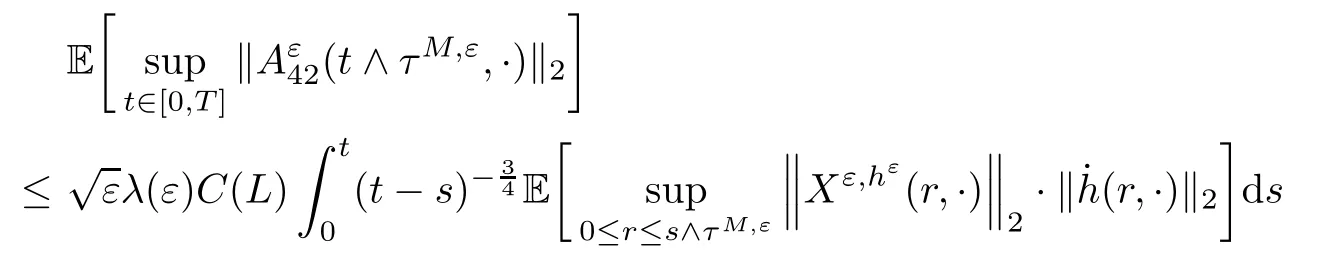

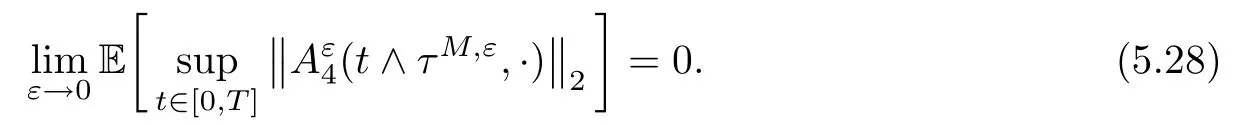


5.4 The proof of Theorem 2.3

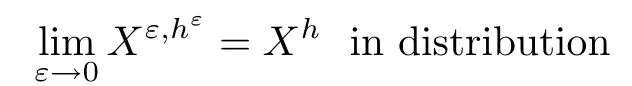
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- ON BOUNDEDNESS PROPERTY OF SINGULAR INTEGRAL OPERATORS ASSOCIATED TO A SCHRDINGER OPERATOR IN A GENERALIZED MORREY SPACE AND APPLICATIONS∗
- GLOBAL WEAK SOLUTIONS FOR A NONLINEAR HYPERBOLIC SYSTEM*
- ASYMPTOTIC STABILITY OF A VISCOUS CONTACT WAVE FOR THE NE-DIMSIAL CPBL VK QU G X*
- BOUNDEDNESS OF VARIATION OPERATORS ASSOCIATED WITH THE HEAT SEMIGROUP GENERATED BY HIGH ORDER SCHRDINGER TYPE OPERATORS∗
- THE EXISTENCE OF A BOUNDED INVARIANT REGION FOR COMPRESSIBLE EULER EQUATIONS IN DIFFERENT GAS STATES*
- THE DAVIES METHOD FOR HEAT KERNEL UPPER BOUNDS OF NON-LOCAL DIRICHLET FORMS ON ULTRA-METRIC SPACES∗
