Weifeng JIANG (蒋伟峰)

College of Science, China Jiliang University, Hangzhou 310018, China

E-mail : casujiang89@gmail.com

Zhen WANG (王振)†

College of Science, Wuhan University of Technology, Wuhan 430071, China

E-mail : zwang@whut.edu.cn

where ρ > 0, s and u are density, entropy and velocity, respectively, andthe energy, with e being the internal energy. R, k, cvand γ are positive constants, and γ >1.

The initial data of (1.1) is

here m= ρu, q = ρE, and ρl,r, ml,r, ql,rare all given constants.

The gas dynamic equation is one of the core subjects of conservation law, in which the existence of global weak solutions with large initial data is the most important problem.

As far as we know, compensated compactness [1]is one of the most effective methods for solving the problem; by using it, the framework of the existence of the solution for isentropic gas dynamic equations with Cauchy data is almost completed. Diperna [2, 3]established the existence of the weak entropy solution for the isentropic Euler equations with general L∞initial data forwhere n ≥2 and n is an integer. Ding, Chen and Luo [4, 5]also got the existence of the isentropic solution by the vanishing numerical viscosity forLions,Perthame, Tadmor and Souganidis [6–8]got the existence results for γ > 3, while Huang and Wang [9]got the existence results for γ =1.

However, the compensated compactness theory encountered bottlenecks [10]in trying to solve the existence of the solution for(1.1)and(1.3)with Cauchy data,because of the difficulty in obtaining a uniform bounded estimation.

As we all know,the invariant region theory is a sufficient way[11]to get the uniform bound estimation in 2×2 conservation laws. For nonlinear systems of conservation laws in several space variables with a known invariant region,the IRP property under the Lax-Friedrichs schemes was studied by Frid in [12, 13]. For the compressible Euler equations, the first order finite volume schemes including the Godunov and Lax-Friedrichs schemes and the positively invariant regions for systems of nonlinear diffusion equations are shown in [14, 15]. However, Frid pointed out that the invariant region theory they obtained is not available in 3×3 conservation laws. Thus,we would like to study the invariant region in 3×3 conservation laws[16]to extend the classical theories and try to obtain the uniform bound estimate.

The aim of the present article is to find a method for obtaining the invariant region of conservation laws with 3 equations. To this end,we calculate the mean-integral of the Riemann solution

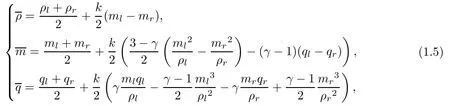
and use the properties of the Riemann invariant region for (1.1). Finally, we get a partial differential equation to calculate the bound equations F = F(ρ,m,q) of the invariant region for (1.1); hereare the mean-integral of ρ, m and q. In addition, we obtain a necessary condition regarding to the state equation to determine the existence of a bounded invariant region for (1.1).

It turns out that there does not exist any bounded invariant region for (1.1) with an ideal gas state, which means the case of non-isentropic gas dynamic equation is quite different from the isentropic case.

This article is organized as follows: in Section 2, we study the Riemann solution of system(1.1)and calculate the mean-integral of the conserved quantity. In Section 3,we mainly discuss the properties of the Riemann invariant region for(1.1),and prove the non-existence of Riemann invariants for (1.1) with an ideal gas state. In Section 4, we propose a necessary condition for the state equation in order to estimate the existence of the bounded invariant region. In Section 5, we provide an example showing that with the special state equation, the bounded invariant regions of (1.1) exist. We state our conclusion in Section 6.

2 The Mean-Integral Conserved Quantity

For (1.1) and (1.4), the three eigenvalues corresponding to the coefficient matrix are

where c is the sound speed and satisfies

To investigate the mean-integral for the conserved quantities of (1.1) and (1.4), we set m= ρu, q = ρE.

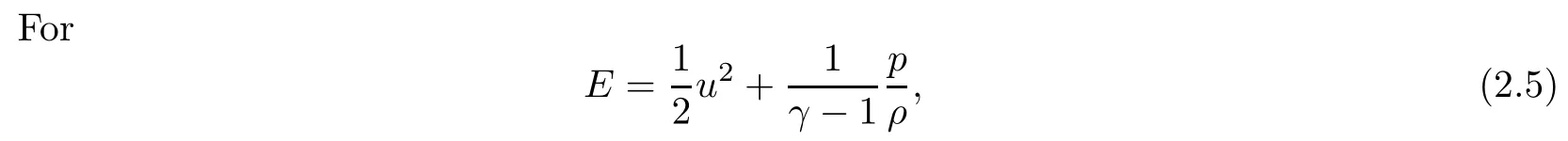
we obtain that

Putting (2.6) into system (1.1), system (1.1) takes the following form:

We define the mean-integral of U as

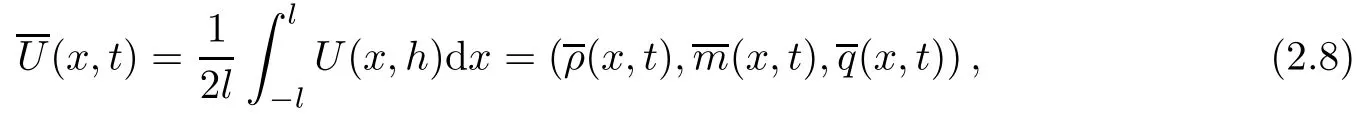
where l and h are the space and time steps.

Then we have following lemma:

ProofWe prove the lemma by the integral along the path Γ (see Figure 1).

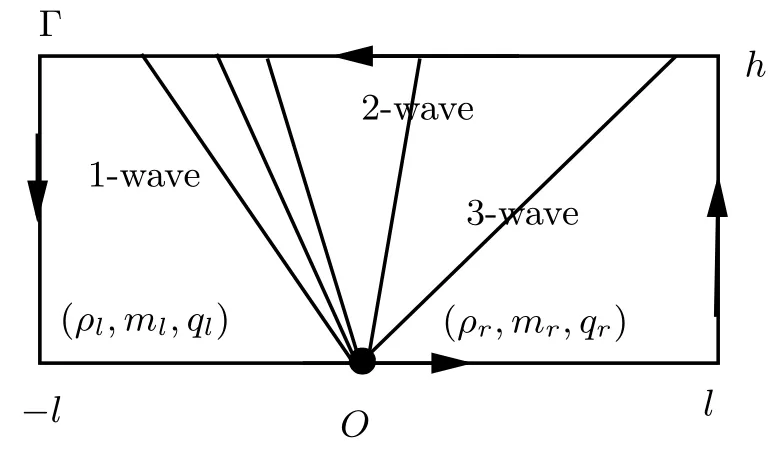
Figure 1 Closed contour integral

By the closed contour integral method,

and we have

3 The Non-existence of a Bounded Invariant Region for Compressible Euler Equations in an Ideal Gas State

In light of Lemma 2.1, we are going to discuss the non-existence of a bounded invariant region for compressible Euler equations in an ideal gas state, which is shown as follows:

Theorem 3.1The bounded invariant region does not exist in the non-isentropic gas dynamic equations in an ideal gas state.

ProofWe suppose that the weak solutions of (1.1) exist as a bounded invariant region Σ. As shown in Figure 2, we set the boundary surface as F(ρ,m,q)= C (here C is a positive constant). Point Ul:=(ρl, ml, ql) satisfies

U :=(ρ, m, q)∈ Σ is a point which belongs to the neighborhood of Ul; that is,

Depending on the convexity of the invariant region Σ, we obtain that the mean-integral istoo, which means thatreached a maximum value at (ρl,ml,ql).

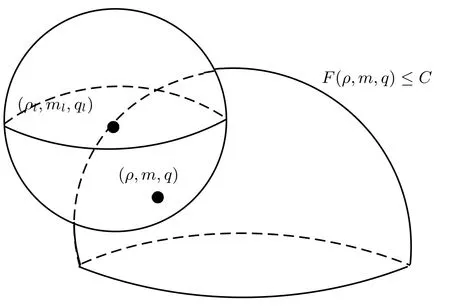
Figure 2 The property of convex invariant region

According to the extremum principle and the Lagrangian multiplier method, ∃λ ∈ R, such that:

To make the statement briefly, we write (3.3) in matrix form:

Expanding (3.4), we see that

Multiplying both sides by

we obtain

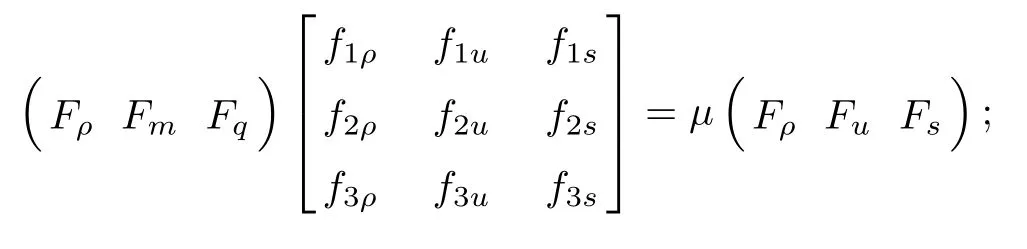
that is,

We also have that

We can now derive the following:

which means that (Fρ,Fu,Fs) is parallel to the left eigenvectors of

Thus, if non-isentropic gas dynamic system(1.1)with initial data(1.4)exists as a bounded invariant region, the boundary equation must be

In other words,

where C is a constant.

q = q(ρ,m) is a convex function in (ρ,m,q) space, which means that the convex invariant region of (1.1) is

It is obvious that such an invariant region is not bounded for ρ, m and q, which leads to the main theorem of our article being the following.

4 The Chosen of State Equation p=p(s,v)

In this section, we focus on the choice of state equation p =p(s,v) if a bounded invariant region of (1.1) exists.

The proofs of (3.5) show us that for a general conservation law with three equations, (3.5)has more than one family of solutions if a bounded invariant region exists.

Due to the smoothness of the boundary equation for the invariant region, converting coordinates has no effect on the conclusions. Thus we write (1.1) into the (v,u,s) space with the undefined state equation p=p(s,v) as follows:

Using the same method as in section 3, we obtain that

The first case is

that is, F =F(s).

The second case is

Solving the first equation of (4.3), we obtain that

Putting (4.4) into the second equation of (4.3) and setting

To make the (4.6) significant, G(s,v) must be the function with respect to s only; that is,

which is equivalent to

To solve (4.8), we expand it as

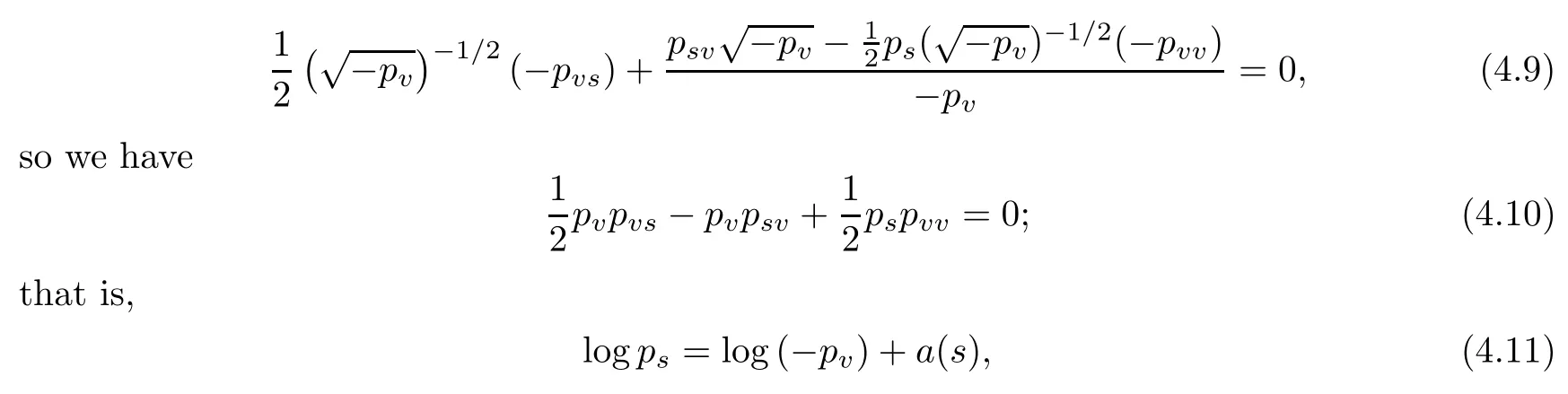
where a(s) is a function with respect to s only.

Lemma 4.1If system (1.1) exists as a closed and convex invariant region, the state equation p=p(s,v) satisfies

where g(x) is a smooth function with gx≥ 0 and gxx≤ 0.

5 Mathematical Example

Here is an example:

Put (5.1) into (4.1) and solve the function F(v,u,s).

The surfaces in the (ρ,m,q) spaces are

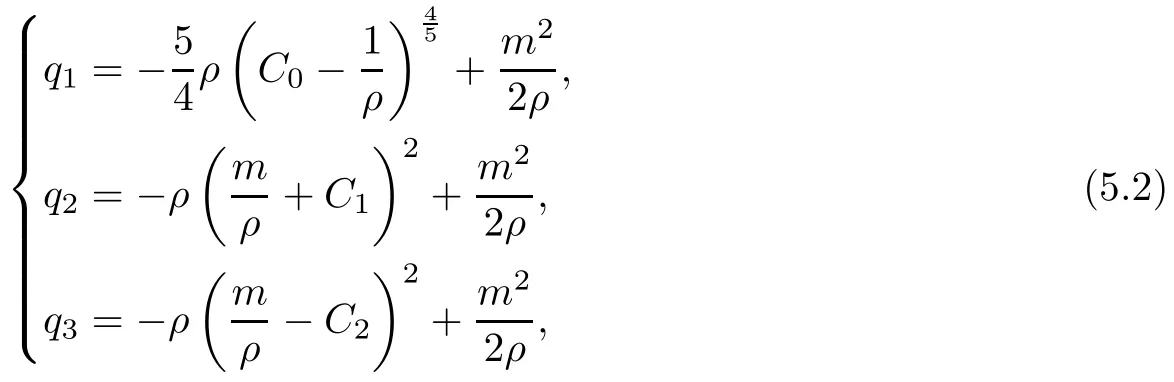
where C0, C1and C2are constants. Thus,

It is clear that q1in the (ρ,m,q)space is a convex function, and that q2and q3are concave functions.

As is shown in Figure 3, the invariant region is represented as

There is no doubt that the space which is covered by q1, q2and q3is a bounded invariant region for (1.1) with the state equation (5.1).

The sidelines are illustrated in Figure 3.

Figure 3 the sidelines

Remark 5.1In fact,the region that is represented by q1and q2is also a bounded invariant region for (1.1) with the state equation (5.1).

6 Conclusion

We conclude that

IThere does not exist any bounded invariant region for one-dimensional non-isentropic gas dynamic equations, which indicates that the compensated compactness theory encounters bottlenecks in non-isentropic gas dynamic equations. There is a big gap between the nonisentropic case and the isentropic case.

IIIf there exists any bounded invariant region for system (1.1), the gas state equation satisfies that

where g(x) is a smooth function with gx≥ 0, gxx≤ 0.

Furthermore, we have found a measure to obtain the bounded invariant region and even calculate its boundary equations for general conservation laws consisting of three equations.We further want to study the sufficient and necessary conditions of the gas state equation for the existence of the bounded invariant region in system (1.1).

AcknowledgementsThe authors of this article would like to thank both Dr. Zhang Tingting from Wuhan Polytechnic University and Wei Xiaoran from Zhejiang University for their help during the writing of this article.