PERIODIC POINTS AND NORMALITY CONCERNING MEROMORPHIC FUNCTIONS WITH MULTIPLICITY*
2020-11-14BingmaoDENG邓炳茂
Bingmao DENG (邓炳茂)
School of Financial Mathematics and Statistics, Guangdong University of Finance,Guangzhou 510521, China
E-mail : dbmao2012@163.com
Mingliang FANG (方明亮)†
Department of Mathematics§Hangzhou Dianzi University§Hangzhou 310012, China
E-mail : mlfang@hdu.edu.cn
Yuefei WANG (王跃飞)
School of Mathematics and Statistics, Shenzhen University, Shenzhen 518060, China;Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China
E-mail : wangyf@math.ac.cn

Let z0∈Dn. If there exists a smallest positive integer n such that fn(z0)=z0, then z0is called a periodic point of period n of f, and the corresponding cycle {z0,f(z0),··· ,fn−1(z0)}is said to be a periodic cycle of period n of f in D. A periodic point of period 1 is called a fixed point. Fordefine the multiplier of the periodic point z0by λ = (fn)′(z0), while for z0= ∞, the multiplier isA periodic point z0is said to be attracting,neutral, or repelling, according to |λ |<1,|λ |=1, or |λ |>1 (see [1, 3]).
There have been many interesting results on normal families of holomorphic or meromorphic functions concerning Hayman’s questions and fixed points (see [1–2, 5–21]). The subject concerning fixed points originated with a problem introduced by Yang ([19, Problem 8]):
Problem 1.1Let F be a family of entire functions, let D be a domain in the complex plane, and let k ≥ 2 be a positive integer. If, for every f ∈ F, both f and its iteration fkhave no fixed points in D, is F is normal in D?
In 1998, Essén and Wu [14]gave an affirmative answer to this question with the following more general result:
Theorem 1.2Let F be a family of holomorphic functions in a domain D. If, for every f ∈ F, there exists a positive integer k =k(f)≥ 2 such that fkhas no fixed points in D, then F is normal in D.
There were a number of further developments initiated by Yang’s question,including these pertaining to meromorphic [6]issues. Other articles related to Yang’s problem include [2, 4–10, 13, 15].
In 2000, Essén and Wu [15]proved that Theorem 1.2 is still valid if fkhas no repelling fixed points in D.
In 2005, Chang and Fang [6]studied Problem 1.1 for when f is a meromorphic function,and they proved
Theorem 1.3Let F be a family of meromorphic functions in a domain D, and let k ≥2 be a positive integer. If, for every f ∈F, fkhas no fixed points in D, then F is normal in D.
There is example in[6]to show that the condition“fkhas no fixed points in D”in Theorem 1.3 cannot be replaced by “fkhas no repelling fixed points in D”.
In 2011, Chang and Zalcman [10]proved
Theorem 1.4Let F be a family of meromorphic functions in a domain D, and let k ≥3 be a positive integer. If, for every f ∈F, f has neither repelling fixed points nor repelling periodic points of period k in D, and all poles of f in D have multiplicity of at least 2, then F is normal in D.
Theorem 1.5Let F be a family of meromorphic functions in a domain D. If, for every f ∈F, f2has no repelling fixed points in D, and all poles of f in D have multiplicity of at least 3, then F is normal in D.
Recently, Deng, Fang and Wang [13]studied the normality under the condition “fkdoes have fixed points in D”, and proved
Theorem 1.6Let F be a family of holomorphic functions in a domain D, and let k ≥2 be a positive integer. If, for each f ∈ F, all zeros of f(z)− z are multiple, and fkhas at most k distinct fixed points in D, then F is normal in D.
Theorem 1.7Let F be a family of meromorphic functions in a domain D,and let k ≥2,l be two positive integers satisfying l ≥ 4 for k =2, l ≥ 3 for k ≥ 3. If, for each f ∈ F, all zeros of f(z)−z have multiplicity of at least l, and fkhas at most one fixed point in D, then F is normal in D.
However,in Theorem 1.7 three assumptions were made on the multiplicities of fixed points of the meromorphic functions related to its k-th iterate, and moreover, the k-th iterate has at most one fixed points. This leaves the following problem:
Problem 1.8Does Theorem 1.6 hold for meromorphic functions if all zeros of f(z)−z are multiple, and fkhas at most k distinct fixed points in D?
In this article, we first obtain the following result on the exact lower bound for the number of the periodic points of rational maps, which is new and rather interesting itself in the sense of rational dynamics:
Theorem 1.9Let R(z)be a non-polynomial rational function,and let k ≥2 be a integer.If all zeros and poles of R(z)− z are multiple, then Rk(z)has at least k+1 fixed points ai∈ C with Rj(ai)∈ C for 0 Then, we give a complete solution to the Problem 1.8, in which Theorem 1.9 plays a key role in the proof. Theorem 1.10Let F be a family of meromorphic functions in a domain D,and let k ≥2 be a positive integer. If, for each f ∈ F, all zeros and poles of f(z)− z are multiple, and fkhas at most k distinct fixed points in D, then F is normal in D. The following examples show that the conditions in Theorem 1.10 are sharp: Example 1.11([13]) Let D ={z :|z |<1}, and let Obviously,fn(z)−z has a single simple zero,and its k-th iterationhas only one fixed point in D, but F is not normal at z =0. This shows that Theorem 1.10 is not valid if “f(z)− z has simple zeros”. Example 1.12([13]) Let D ={z :|z |<1}, and let Obviously,fn(z)−z has a multiple zero,andhas exactly three fixpoints in D, but F is not normal at z =0. This shows that the condition “fkhas at most k fixed points in D” is sharp in Theorem 1.10. Example 1.13([13]) Let D ={z :|z |<1}, and let Obviously,fn(z)−z has a simple pole. By mathematical induction,we obtain,for any k ∈ N+, Example 1.14([13]) Let D ={z :|z |<1}, and let Obviously, fn(z)−z has a simple pole, and Moreover, we have the following result, which is a consequence of Theorem 1.10: Theorem 1.15Let F be a family of meromorphic functions in a domain D,and let k ≥2 be a positive integer. If, for each pair f,g ∈ F, all zeros and poles of f(z)−z are multiple, and fkand gkshare fixed points in D, then F normal in D. For the proofs of our results, we need the following lemmas: Lemma 2.1([11, 18, 21]) Let F be a family of meromorphic functions in the unit disc ∆such that all zeros of functions in F have multiplicity ≥ p. Let α be a real number satisfying−p<α<1. Then F is not normal in any neighborhood of z0∈∆ if and only if there exist a) points zj∈ ∆, zj→ z0; b) functions fj∈F; and c) positive numbers ρj→ 0 such that gj(ξ)=spherically uniformly on compact subsets of C, where g(ξ) is a non-constant meromorphic function satisfying that all zeros of g have multiplicity of at least p. Lemma 2.2([3]) Let f be a transcendental meromorphic function, and let k ≥2 be a positive integer. Then the k-th iteration fkhas infinitely many fixed points in C. Lemma 2.3([1]) Let R(z) be a rational function, and let l(≥ 2),k(≥ 2) be two positive integers. If α is a zero of R(z)− z with multiplicity l, then α is a zero of Rk(z)− z with multiplicity l. Lemma 2.4([7, 13]) Let R(z) be a rational function with degree d ≥ 2, and let k ≥ 2 be an integer. Then R(z) has at least 2k periodic points of period k, except for in the cases(k,d)∈{(2,2),(2,3),(2,4),(3,2),(4,2)}. Lemma 2.5([13]) Let P(z)be a polynomial such that all zeros of P(z)−z are multiple,andwhere A,B ∈ C, and let k ≥ 2 be an integer. Then Pk(z) has at least k+1 fixed points aiwith Pj(ai)∈ C for 0 The precise calculations of periodic points of rational functions are extremely complicated.The main ingredient of our proof is to combine reasoning with conformal conjugations, as well as calculations making use of Maple 17. For two given holomorphic or meromorphic functions f and g, f and g are said to be conformal conjugate if there exists a conformal map M(z) in the plane such that g(z)=M ◦ f ◦ M−1(z). In the whole plane case, M(z) is in fact a Mbius(affine) transformation:Then f and g share many dynamical properties,such as the same number of periodic points with the same period,the same number of critical points and poles with the same multiplicity, etc.. Conformal conjugation helps to simplify our discussions considerably, and Maple 17 helps for precise calculations. ProofWe consider four cases. Case 1R has no fixed point. Then we may set where P is a monic polynomial of degree m ≥ 2, all zeros of P(z) are multiple, andis a constant. In this section, since we are only concerned here with the number of periodic points and since two conjugated functions have exactly the same number of periodic points with the same period, we may always denote, without loss of generality, the conjugated function of the given function (by conformal conjugation with a suitable conformal map) as itself, for simplicity. Hence by conformal conjugation, we may simply assume that It follows from (3.2) that deg R=m+1 ≥3. Then, by Lemma 2.4, we deduce that R has at least 2k periodic points with period k except for in the cases (k,m)∈{(2,2),(2,3)}. Case 1.1(k,m)=(2,2). Thenwhere a is constant. By conformal conjugation, we may assume, without loss of generality, that Then we have where Q2(z) = (z3+ 1)2+ z6= 2z6+ 2z3+ 1. Obviously, Q2and P2are two co-prime polynomials. If Q2(z) has at most two distinct zeros, then Q2(z) has a zero z0with multiplicity of at least three, as deg Q2=6. Case 1.2(k,m)=(2,3). Thenwhere a is constant. Again by conformal conjugation, we may assume, without loss of generality, that Then we have where Q3(z)=(z4+1)3+z12=2z12+3z8+3z4+1. Obviously, Q3and P3are two co-prime polynomials. If Q3(z) has at most two distinct zeros, then Q3(z) has a zero z0with multiplicity of at least 6, as deg Q3=12, and obviously, Hence, Rkhas at least k+1 distinct fixed points z1,··· ,zk+1. Next, we need only to show that no such zi(i=1,··· ,k+1) can be mapped to ∞ by any Rjwith j Case 2R has exactly one fixed point. Then we may set where P is a monic polynomial of degree m ≥ 2,all zeros of P(z)are multiple,is a constant, and l ≥2. Next, we consider four subcases. Case 2.1m ≥ l. It follows from (3.3) that deg R = m+1 ≥ 3. Next, we consider three cases. Case 2.1.1(k,m)Then by Lemma 2.4,we know that R has at least 2k periodic points of period k. Hence, there exist at least two cycles: where Rj(zi) (i = 1,2) (1 ≤ j ≤ k) are 2k distinct complex numbers. Then at least one cycle lies in the plane C, so we assume that Rj(z1) ∈ C (1 ≤ j ≤ k). Combined with a is a fixed point of Rk(z), hence Rk(z) has at least k+1 distinct fixed points z1,··· ,zk+1with Rj(zi) ∈ C for 0 Case 2.1.2(k,m)=(2,2). We deduce that l =2, so (3.3) can be written as Then we have where Q4(z) = [z3+(z − a)2]2+z2[z2+(z − a)]2= 2z6+ ···+a4. Obviously, Q4and P4are two co-prime polynomials, andHence, there existand a, such that Q4(z1)=z1. Thus, z1is a periodic point of R with period 2, so there exists a corresponding periodic cycle {z1,z2= R(z1)} of R. Obviously,and, combing this with R(∞) = ∞, we obtain that R2has at least three distinct fixed points z1,z2,z3satisfying R(zi)∈C,i=1,2,3. Case 2.1.3(k,m) = (2,3). Then l = 2 or l = 3, because 3 = m ≥ l ≥ 2. Next we consider two cases. Case 2.1.3.1l=2. Then (3.3) can be written as where Q5(z)=[z4+(z − a)2]3+[z3(z − a)]2z6=2z12+ ···− a6. Using the same argument as in Case 2.1.2, we get that R2(z) has at least three distinct fixed points with R(zi)∈C,i=1,2,3. Case 2.1.3.2l=3. Then (3.3) can be written as where Q6(z) = [z4+(z − a)3]3+[z3+(z − a)2]3z3= 2z12+6z11+ ···− a9. Using the same argument as in Case 2.1.2, we get that R2(z) has at least three distinct fixed points with R(zi)∈C,i=1,2,3. Case 2.2l ≥ m+2. It follows from(3.3)that deg R=l ≥ 4. Using the same argument as in Case 1.1,we deduce that Rk(z)has at least k+1 fixed points,z1,··· ,zk+1, with Pj(zi) ∈ C for 0 Since 4=l ≥ m+2 ≥ 4, it is easy to get that m=2. Then (3.3) can be written as Without loss of generality,we may assume once again(by conformal conjugation with a suitable conformal map) that It follows from (3.11) that where Q7(z)=z2[z3+(z − a)4]2+[z2+(z − a)3]4=z12+(4 − 12a)z11+ ···+a12. Using the same argument as in Case 2.1.2, we obtain that R2(z) has at least three distinct fixed points with R(zi)∈C,i=1,2,3. Case 2.3l=m+1 andIt follows from(3.3)that deg R=l=m+1 ≥ 3. Using the same argument as in Case 2.1.2, we deduce that except for (k,l) ∈{(2,3),(2,4)}, Rkhas at least three distinct fixed points. Next, we consider the case (k,l)∈{(2,3),(2,4)}. Case 2.3.1(k,l)=(2,3). Then (3.3) can be written as Without loss of generality, we may assume once again (by conformal conjugation with a suitable conformal map) that It follows from (3.11) that where Q8(z)=[(z − 1)3+Az3]2+[(z − 1)2+Az2]3=(A3+4A2+5A+2)z6− (6A2+18A+12)z5+(3A2+24A+30)z4+ ···+2. First, we show that deg Q8(z) ≥4 (and therefore has at least one zero). Otherwise, we have three equations: Obviously, there is no solution to the equations, which is a contradiction. Obviously, Q8(1) = A2(1+A)Then, there existssuch that Q8(z1) = 0, hence, z1is a periodic point of R with period 2, so there exists a corresponding periodic cycle {z1,z2= R(z1)} of R. Obviously,and combing this with R(∞)=∞, we obtain that R2has at least three distinct fixed points z1,z2,z3(=a) satisfying R(zi)∈C,i=1,2,3. Case 2.3.2(k,l)=(2,4). Then (3.3)) can be written as Without loss of generality, we may assume once again (by conformal conjugation with a suitable conformal map) that It follows from (3.13) that where Q9(z)=[(z − 1)4+Az4]3+[(z − 1)3+Az3]4=(A4+5A3+9A2+7A+2)z12+ ···+12.Using the same argument as in Case 2.3.1,we obtain that R2(z)has at least three distinct fixed points with R(zi)∈C,i=1,2,3. Case 2.4l=m+1 and A=−1. Then (3.3) can written as Obviously,Q(z)and P(z)are co-prime,sinceHence deg R=m ≥ 2. Using the same argument as in Case 1.1, we deduce that except for (k,m) ∈{(2,2),(2,3),(2,4),(3,2),(4,2)},Rk(z)has at least k+1 fixed points,z1,··· ,zk+1,with Pj(zi)∈ C for 0 Next, we consider the cases (k,m)∈{(2,2),(2,3),(2,4),(3,2),(4,2)}. Case 2.4.1(k,m)=(2,2). Then (3.3) can be written as Without loss of generality, we may assume once again (by conformal conjugation with a suitable conformal map) that Q10(z)=9z2− 8z+2=obviously,and Q10(z)has two distinct zeros. Hence R2(z) has at least three distinct fixed points with R(zi)∈C,i=1,2,3. Case 2.4.2(k,m)=(2,3). Then (3.3) can be written as Without loss of generality, we may assume once again (by conformal conjugation with a suitable conformal map) that It follows from (3.17) that where Q11(z)=64z6− 117z5+ ···+2. Using the same argument as in Case 2.4.1, we obtain that R2(z) has at least three distinct fixed points with R(zi)∈C,i=1,2,3. Case 2.4.3(k,m)=(2,4). Then (3.3) can written as Again, by conjugation, we may assume that It follows from (3.19) that then we have Q12(z)= −625z12+···−2. Using the same argument as in Case 2.4.1,we obtain that R2(z) has at least three distinct fixed points with R(zi)∈C,i=1,2,3. then we get that Q12(z) = C12z12+C11z11+ ···+C1z +C0, with Cj(0 ≤ j ≤ 12) being constants depending on b1and b2. First, we claim that deg Q12(z)≥11. Otherwise, we would have C12=0,C11=0. Solving the equations, we get that b1= b2= 0; a contradiction. The claim is proved. Hence, Q12(z)has at least one zero z1, and z1is a periodic point of R of period 2. By Lemma 2.3, we know that If Q12(b1) = 0 and Q12(b2) = 0, then solving the equations, we get b1= b2= 0, which is a contradiction. Hence, we obtain that if Q12(b1) = 0, thenif Q12(b2) = 0, then Suppose that Q12(b1) = 0. ThenWe claim that there existsuch that Q12(z1)=0. Otherwise, b1would be a zero of Q12(z) with multiplicity of at least 11,and thenSolving the equations, we would obtain b1=0; a contradiction. Using the same argument as above, we obtain that R2(z) has at least three distinct fixed points with R(zi)∈C,i=1,2,3. Case 2.4.4(k,m)=(3,2). Then (3.3) can be written as By conformal conjugation again, we may assume that Then we have Case 2.4.5(k,m)=(4,2). Then (3.3) can be written as Again we have Hence, R4(z) have at least 5 distinct fixed points: z0(= 0),z1,z2,z3,z4. We claim that z0(= 0),z1,z2,z3,z4, satisfying that Rj(zi) ∈ C for 0 ≤ i ≤ 4,j = 1,2,3. Otherwise, if we were to suppose that there exist zi0(1 ≤ i0≤ 4) such that Rj0(zi0) = ∞, then Rj0+1(zi0) =R(∞)= −2, and thus Rj0+1(zi0)=R(∞)= −2 would also be a zero of Q14(z), but this would contradict the fact that Q14(−2)= −88270967484 =0. The claim is proved. Case 3R(z) has exactly two distinct fixed points. Then we may set where P(z) is a non-constant monic polynomial with all zeros with multiplicity of at least 2,andSet deg P(z)=m,L=l1+l2. Next we consider four cases. Case 3.1m ≥ L. Then deg R(z) = m+1 ≥ L+1 ≥ 5, and, by Lemma 2.4, we deduce that R has at least 2k periodic points with period k. Using the same discussion as in case 2.1.1,we obtain that Rk(z) has at least k+1 distinct fixed points, z1,··· ,zk+1, with Rj(zi) ∈ C for 0 Case 3.2L ≥ m+2. Then deg R(z)=L ≥ 4. It follows from case 3.1 that we only need to consider the cases L = 4 and k = 2, which implies that l1= l2= m = 2, so (3.20) may be written as where a1,a2,b are three distinct constants, andis a constant. Without loss of generality,we may assume once again (by conformal conjugation with a suitable conformal map) that Then we obtain Case 3.3L = m+1 andThen deg R(z) = L ≥ 4. Using the same discussion as in Case 3.2, we only need to consider the cases L = 4 and k = 2, that is, l1= l2= 2 and m=3, so (3.20) may be written as where a1,a2,b are three distinct constants, andis a constant. Without loss of generality, we may assume once again (by conformal conjugation with a suitable conformal map) that Then we have Then Q16(z) has at least one zero. We claim thatOtherwise, suppose that Q16(0)=0. Then we obtain that a1=0 or a2=0, which is a contradiction. Hence, R2(z) have at least three fixed points, a1,a2,a3, satisfying R(ai)∈C. Case 3.4L = m+1 and A = −1. Then deg R(z) = m = L − 1 ≥ 3. Using the same discussion as in case 3.2, we only need to consider the cases (k,L)∈{(2,4),(2,5)}. Case 3.4.1(k,L)=(2,4). Then m=L −1=3,and combing this with all zeros of P(z),we have multiplicity of at least 2. Then (3.20) may be written as where a1,a2,b are three distinct constants. By conformal conjugation again, we assume that Then we have Using the same discussion as in Case 3.3, we deduce that deg Q17(z)≥5. Next, we claim that there existssuch that Q17(a3) = 0. Otherwise, Q17(z) has only one zero 0 as deg Q17(z) ≥5, so 0 is a zero of Q17(z) with multiplicity of at least 5, andsolving the equations, we obtain a1=0 or a2=0; a contradiction. Hence, R2(z) have at least three fixed points, a1,a2,a3, satisfying R(ai)∈C. Case 3.4.2(k,L)=(2,5). Then m=L −1=4,and combing this with all zeros of P(z),we have multiplicity of at least 2. Then P(z)=(z − b)4or P(z)=(z − b1)2(z − b2)2. Next, we consider two subcases. Case 3.4.2.1P(z)=(z −b)4. Then (3.20) can be written as where a1,a2,b are three distinct constants. By conformal conjugation, we may assume that Hence, R2(z) have at least three fixed points, a1,a2,a3, satisfying R(ai)∈C. Case 3.4.2.2P(z)=(z − b1)2(z − b2)2. Then (3.20) can be written as where a1,a2,b1,b2are four distinct constants. By conformal conjugation, we may assume that Again we obtain We claim that deg Q19(z) ≥10. Otherwise, we obtain C12= 0,C11= 0,C10= 0, and solving the equations, we obtain b1=0 or b2=0, which is a contradiction. The claim is proved. In fact, where A1= (z − b1),A2= (z − b2),B = (z − b1)2(z − b2)2,C = z3(z − a2)2,D1= (z − a2),D2=z, E =z2(z −a2). If Q19(b1)=0,Q19(b2)=0, it follows from (3.25) that −2(b1− b2)+3b1+2(b1− a2)=0,−2(b2− b1)+3b2+2(b2− a2)=0. Solving the equations, we obtain b1=b2; a contradiction. If Q19(b1) = 0, thenWe claim that there existssuch that Q19(a3) = 0. Otherwise, Q19(z) has only one zero b1, and we havebut if Q19(b1) = 0, by (3.25), we have −2(b1− b2)+3b1+2(b1− a2) = 0, andthis is, again, a contradiction. Hence, R2(z) have at least three fixed points, a1,a2,a3, satisfying R(ai)∈C. Case 4R(z) has at least three distinct fixed points. Then we deduce that deg R ≥5,and by Lemma 2.4, we know that R has at least 2k periodic points of period k. Using the same argument as in case 2.1.1, we obtain that Rk(z) has at least k+1 distinct fixed points,z1,··· ,zk+1, with Rj(zi)∈ C for 0 This completes the proof of Theorem 1.9. Let H={h:h(z)=f(z)− z;f ∈ F}. Since all zeros and poles of f(z)− z are multiple in D, then for any h ∈G, all zeros and poles of g are multiple in D. Obviously,F is normal in D if and only if H is normal in D. Next, we prove Theorem 1.10 by the method of Chang and Fang [6]. Suppose that H is not normal at z0∈D. Then, by Lemma 2.1, there exists a sequence znof complex numbers with zj→ z0, a sequence ρjof positive numbers with ρj→ 0 , and a subsequence of {hj}⊆H, such that locally uniformly with respect to the spherical metric on C,where H is a nonconstant holomorphic function on C. By Hurwitz’ Theorem, all zeros and poles of H are multiple. From (4.1)–(4.3), it is easy to get We claim that for any n ∈N, Next we prove the claim by mathematical induction. The claim is true for n=1 by (4.4).Assume now that it is true for n ≥1. By (4.2) and (4.5), we have By (4.4)–(4.6), we obtain Thus, the claim is true, and by (4.5), we obtain By (4.1) and (4.3), we obtain locally uniformly on C/{F−1(∞)}. Then by (4.5), (4.9) and (4.10), for any n ∈ N+, as j → ∞, locally uniformly on C/E. If Fk(ξ)has at least k+1 distinct fixed points ξi∈ C(i=1,··· ,k+1)satisfying Fn(ξi) ∈ C for n ∈ {1,2,··· ,k − 1}, then there exists a positive number δ such that Di= Dδ(ξi) = {ξ :|ξ − ξi| < δ} ⊂ C/E (i = 1,··· ,k+1) and such thatThus, by (4.8), (4.11) and Hurwitz’s Theorem, for sufficiently large j, there exist points ξj,i→ξi(i = 1,··· ,k +1) such thatNotice that Dj(ξj,i) − Dj(ξj,i) = zj+ ρjξj,i→ z0∈ D as j → ∞. This means thathas at least k + 1 distinct fixed points zj+ ρjξj,i(i = 1,··· ,k + 1) in D for sufficiently large j, but from the assumption thathas at most k fixed points in D, we obtain that there exists 1 ≤ i1< i2≤ k+1 such that ξj,i1= ξj,i2. This is in contradiction with the fact that Hence Fkhas at most k fixed points in C. Thus, by Lemma 2.2, Lemma 2.5 and Theorem 1.9, we deduce that F(ξ) = Aξ+B, where A,B are two constants. It follows from (4.9) that H(ξ) = (A − 1)ξ+B. If A = 1, then H is a constant; a contradiction. Ifthen G only has a simple zero, which contradicts the fact that all zeros of H are multiple. Hence H is normal in D, so F is normal in D. This completes the proof of Theorem 1.10.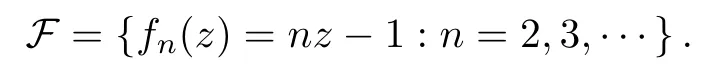
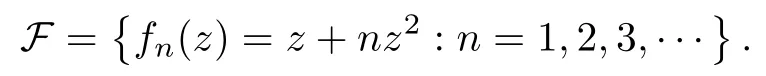
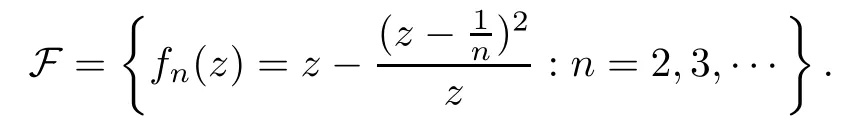
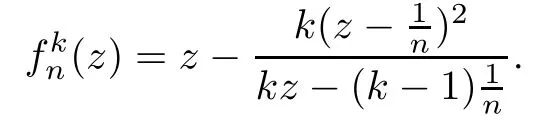

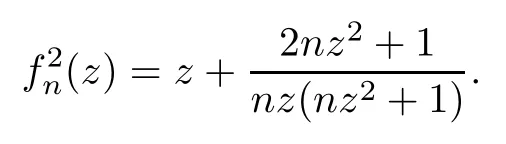
2 Preliminary Results
3 Proof of Theorem 1.9




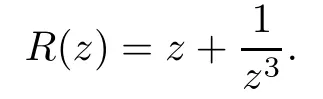
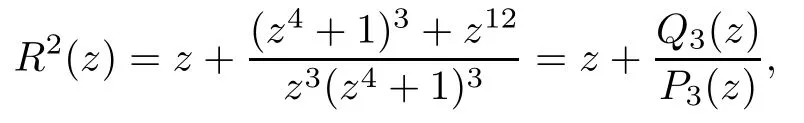
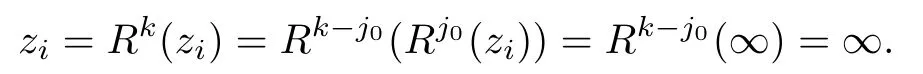






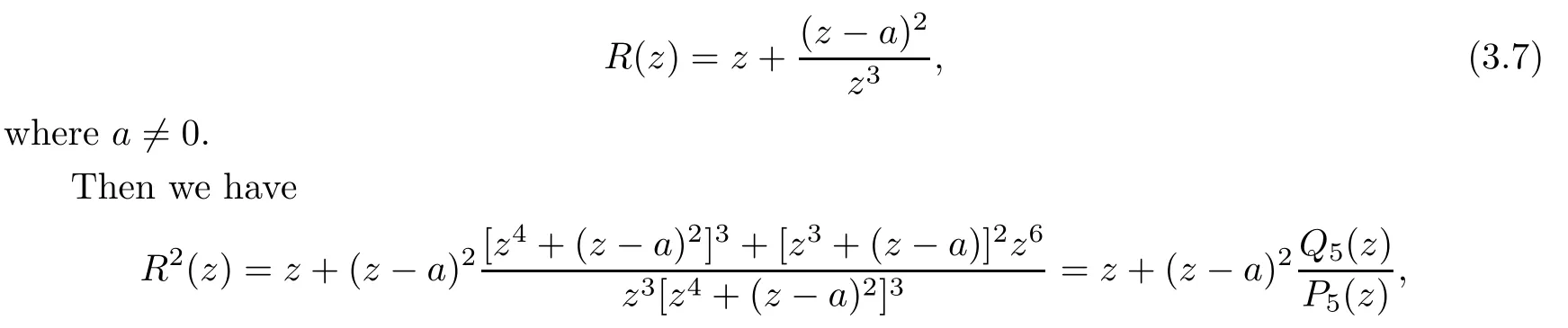
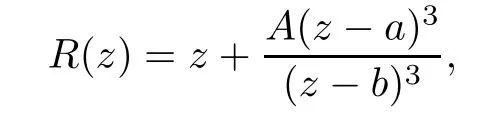



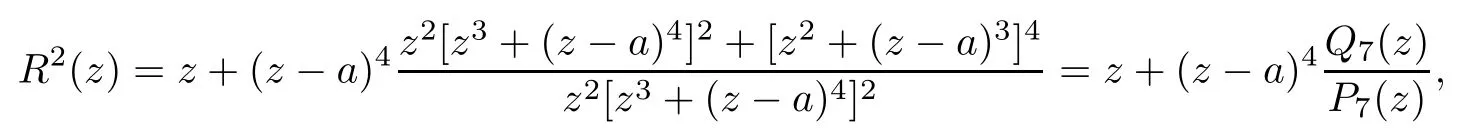
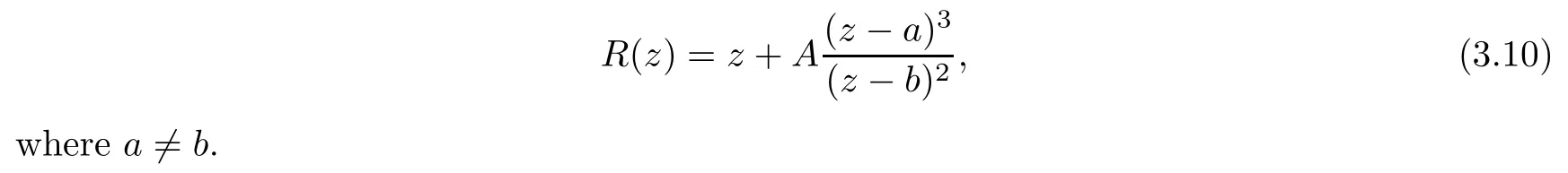

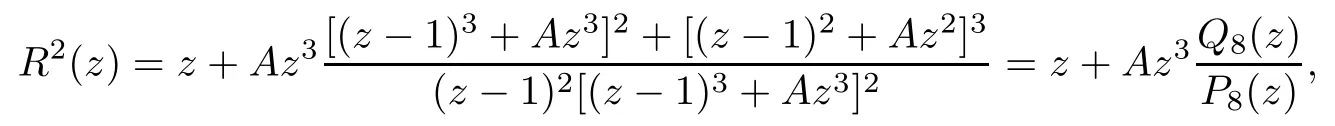
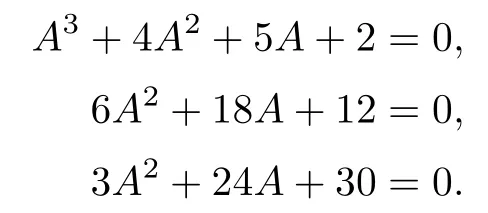


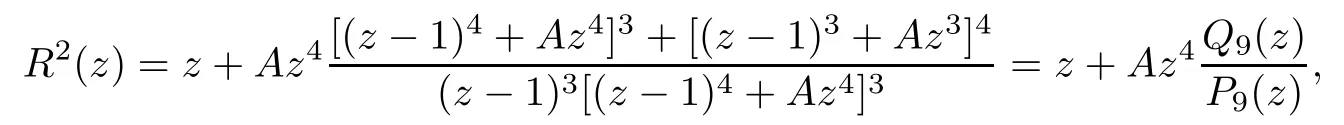

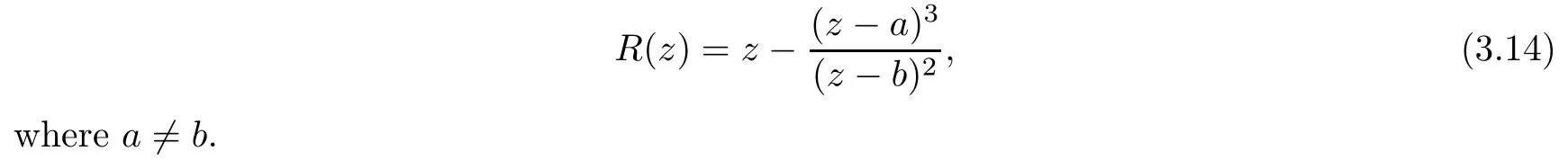



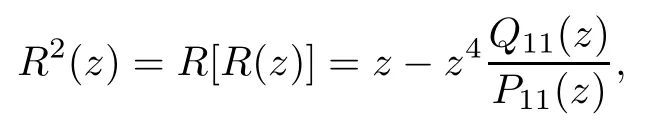

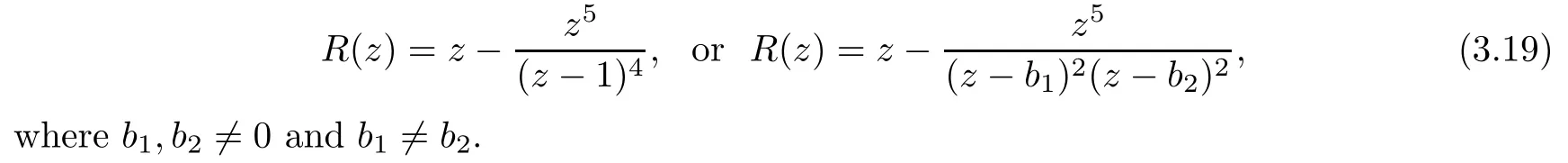






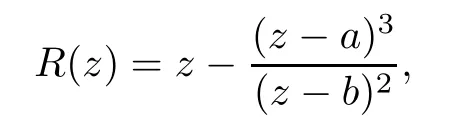

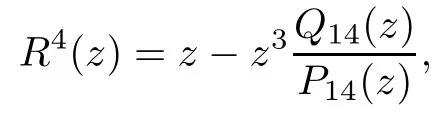
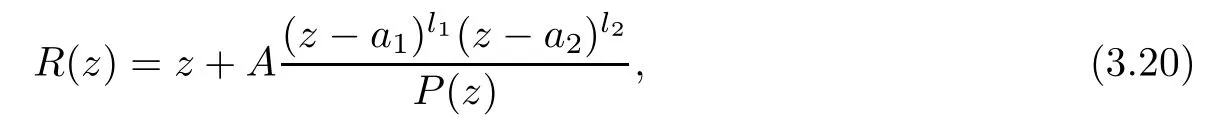

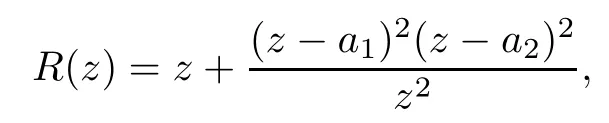



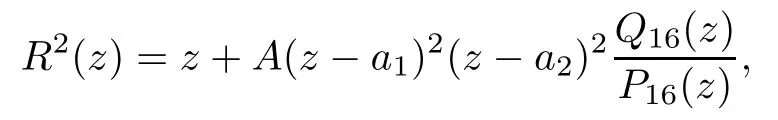
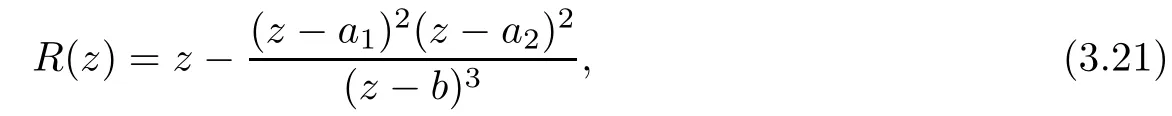
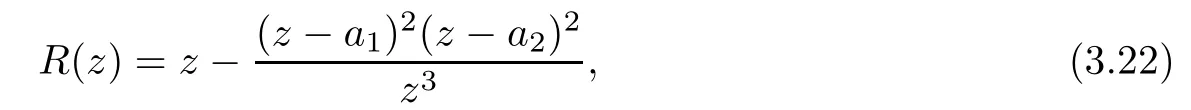




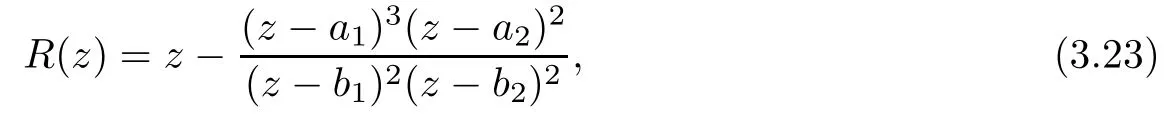
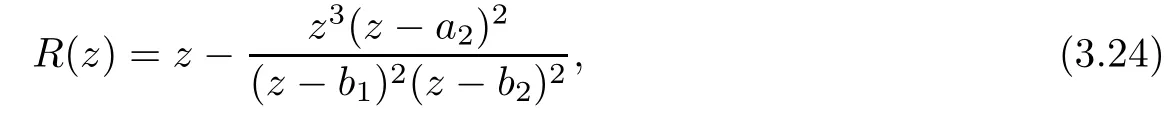


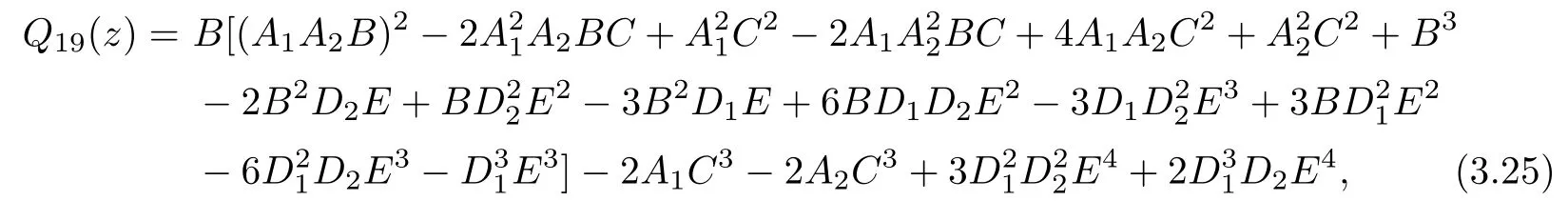
4 Proof of Theorem 1.10
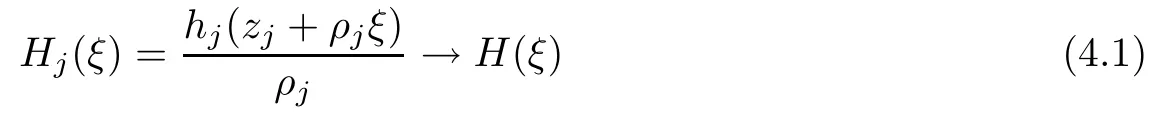



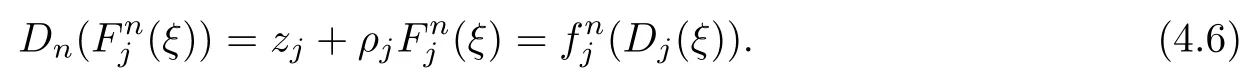
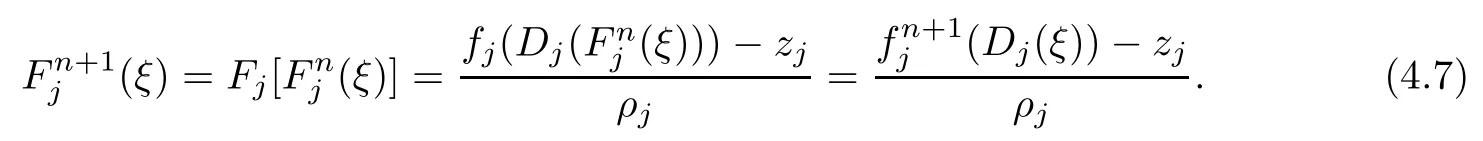
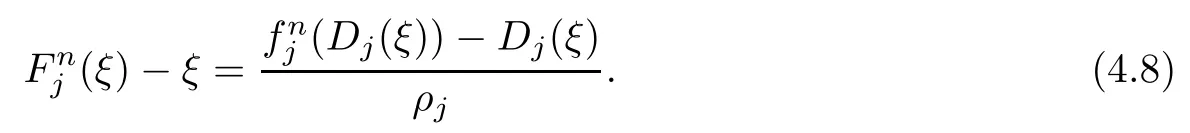
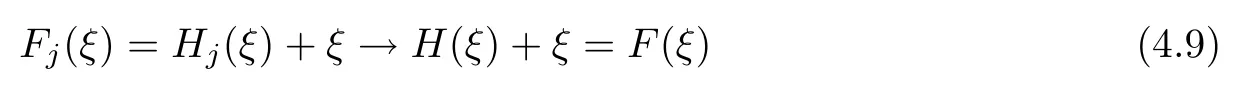
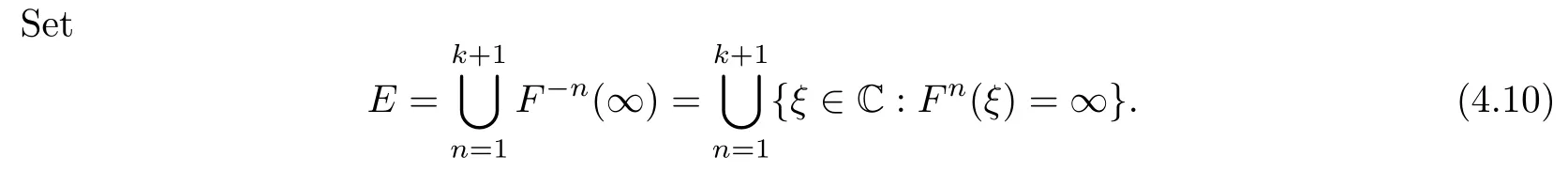

杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- ON BOUNDEDNESS PROPERTY OF SINGULAR INTEGRAL OPERATORS ASSOCIATED TO A SCHRDINGER OPERATOR IN A GENERALIZED MORREY SPACE AND APPLICATIONS∗
- GLOBAL WEAK SOLUTIONS FOR A NONLINEAR HYPERBOLIC SYSTEM*
- ASYMPTOTIC STABILITY OF A VISCOUS CONTACT WAVE FOR THE NE-DIMSIAL CPBL VK QU G X*
- BOUNDEDNESS OF VARIATION OPERATORS ASSOCIATED WITH THE HEAT SEMIGROUP GENERATED BY HIGH ORDER SCHRDINGER TYPE OPERATORS∗
- THE EXISTENCE OF A BOUNDED INVARIANT REGION FOR COMPRESSIBLE EULER EQUATIONS IN DIFFERENT GAS STATES*
- THE DAVIES METHOD FOR HEAT KERNEL UPPER BOUNDS OF NON-LOCAL DIRICHLET FORMS ON ULTRA-METRIC SPACES∗
