基于高阶单元的滑动轴承润滑特性计算
2020-11-13杨国栋张文平曹贻鹏明平剑李燎原
杨国栋, 张文平, 曹贻鹏, 明平剑, 李燎原
(1.哈尔滨工程大学 动力与能源工程学院,黑龙江 哈尔滨 150001;2.中国舰船研究设计中心,湖北 武汉 430064)
滑动轴承在工业生产和生活领域中应用较广,具有承载力大、稳定性好等特点[1]。正常工作时,轴和轴瓦之间会形成楔形的几何空间,润滑油在界面运动的带动下进入该间隙,进而形成动压强,起到承受外载荷和减小摩擦力的作用。雷诺方程是求解滑动轴承润滑特性的基本方程,一维雷诺方程具有解析解,但是这类方程左侧缺少了1个方向的泊肃叶流项,会导致计算得到的压强值偏大,不符合实际情况。二维雷诺方程可以很好地描述有限宽轴承的压强分布,但是没有解析解,通常采用数值法求解。有限差分法[2-7]是较常用的数值解法,该算法用差商来代替导数,形式简单,但只能处理正交化的四边形网格,不适用于复杂的计算域;有限元法[8-10]从弹性力学发展而来,后来应用于润滑分析中,求解域的网格划分更为灵活,节点压强梯度可以采用单元形函数导数的方式处理,但该算法需要构建较大的刚度矩阵,计算消耗较大;非结构有限体积法兼具有限体积法守恒性的特点和对复杂区域良好适用性的特点,在传热学[11]和结构领域[12-13]应用较多,在润滑领域应用较少[14-15],并且尚未涉及高阶单元,而随着对计算精度和效率的要求不断提高,有必要从高阶单元的角度出发开展相关研究。
本文使用六节点三角形单元划分求解域,采用多重网格法求解离散的代数方程组,进而研究轴承的润滑特性。
1 润滑理论方程及雷诺方程的离散
矢量形式的雷诺方程为:

(1)
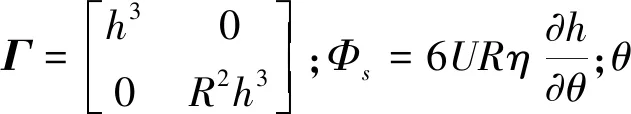
轴承的几何关系如图1所示。
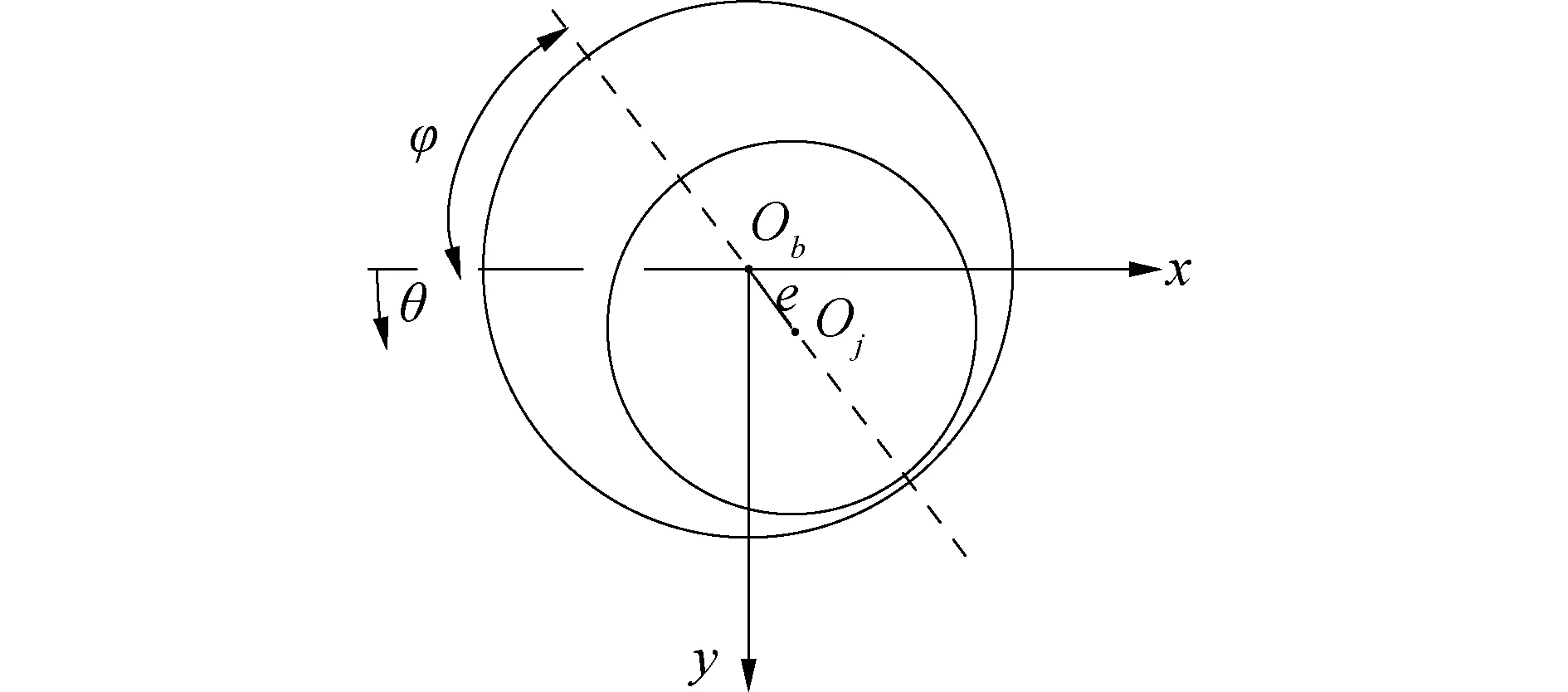
图1 轴承几何关系Fig.1 Geometric position of journal bearing
设轴心坐标为(x,y),径向滑动轴承的液膜厚度为:
h=c+ecos(θ-φ)=
c+ecosφcosθ+esinφsinθ=
c+xcosθ+ysinθ
经过调研分析,对于系统功能的需求主要分为对基础地理信息的查询和操作功能、配方施肥决策功能和用户管理功能3个方面。基础GIS功能主要包括地图缩放及漫游、查询、图层显示及控制、测量功能;配方施肥决策功能主要包括养分含量查询功能、施肥配方决策功能、土壤肥力评价功能等;用户管理功能主要包括用户注册、认证、权限管理等功能。系统功能结构见图2。
(2)
式中:c为轴承间隙;e为偏心距;φ为偏位角。油膜反力方程、端泄方程和摩擦系数方程参考文献[1-2]。
平均误差计算公式为:
(3)
式中:m表示润滑区域的节点总数;pi表示各个算例中的节点压强;pi,ref表示参考节点压强。
图2为本文采用的2类三角形单元及其节点的示意图,A~F表示节点,内部空心点为积分点。格点型有限体积法的控制体是围绕节点形成的,如图3所示,在控制体内,对式(1)积分可得:
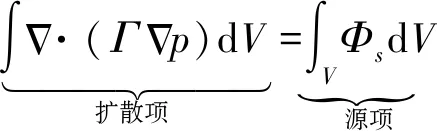
(4)
扩散项可按下式进行离散:
(5)
式中:nc表示节点周围的单元数;ncni表示第i个单元的节点总数;N代表形函数;nα(α=x,y)为面单位外法线失量n沿α方向的分量;ψ表示围绕控制体的积分线。

图2 2种三角形单元示意Fig.2 Two kinds of triangular elements
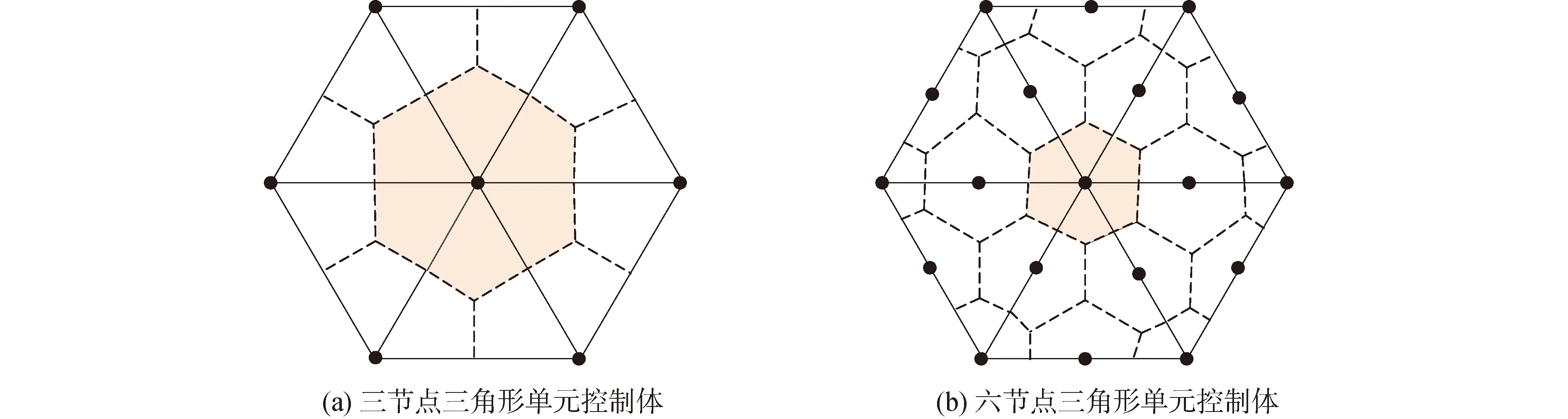
图3 控制体和积分点示意Fig.3 The control volume and its integration points
源项离散为:
(6)
则式(4)可转化为:
(7)
2 形函数的处理
2.1 常应变三角形单元
如图4所示,1~3为三角形单元的3个节点,A、B、C分别为边L12、L23、L31的中点,O为单元中心,型函数等信息可参考文献[17],积分点坐标可由几何关系获得。
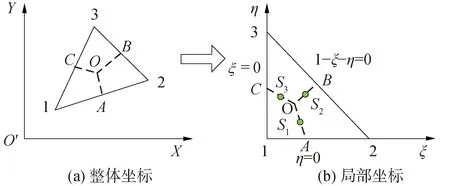
图4 三节点三角形单元的坐标转换Fig.4 Coordinate transformation of 3-node triangular element
在节点周围的第i个单元内,形函数导数沿控制体边界的积分为:
(j=1,2,3;α=x,y)
(8)
式中Ljα为围绕第j个节点的积分线在α方向上的投影长度。
利用雅克比矩阵,经过推导可得型函数对全局坐标的导数为:

(9)
式中:(x1,y1)、(x2,y2)、(x3,y3)分别为全局坐标下三角形节点1、2、3的节点坐标;S123为全局坐标下三角形单元的面积。
2.2 六节点三角形单元
如图5所示,1~6为高阶三角形单元的6个节点编号,S1~S9为高斯积分点的编号,六节点三角形单元的形函数和积分点坐标见文献[17]。
在节点周围的第i个单元内,形函数导数沿控制体边界的积分为(其余推导同2.1):
(j=1,2,3,4,5,6;α=x,y)
(10)
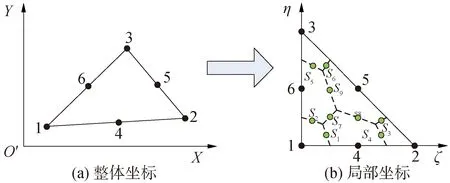
图5 六节点三角形单元的坐标转换Fig.5 Coordinate transformation of 6-node triangular element
3 轴承实例分析
本文的计算程序是在哈尔滨工程大学动力装置工程技术研究所自主开发的通用输运方程求解器GTEA软件的基础上开发的,采用Fortran90语言编程,在参数为4 GB RAM、Intel Core i5-2400、CPU 3.1 GHz的计算机中运行程序。
3.1 算法准确性验证
本节采用文献[2]中滑动轴承的计算结果来验证算法的准确性,轴承半径为30 mm,长度为66 mm,间隙为0.03 mm,粘度为0.009 Pa·s,转速为3 000 r/min。网格划分如表1所示,其中Case0为验证算例所用的模型,采用四边形网格划分,其结果也将用于下一节中的分析。由图6可得,Case0的压强分布与文献[2]中的结果基本一致;由表2可得Case0的最大压强、端泄流量、摩擦系数与文献均较接近,因此,非结构格点型有限体积法的正确性得以验证,该算法可用于下一步的分析。
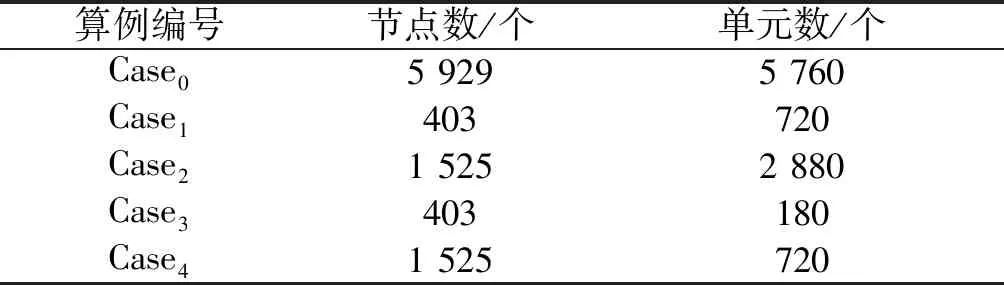
表1 网格划分结果Table 1 Grid meshing results

表2 油膜压强最大值的对比

图6 Case0压强分布准确性验证Fig.6 Verification of the accuracy of pressure distribution of Case0
3.2 高阶单元的结果对比
本节采用表1中的算例研究高阶单元的影响,其中,Case1和Case2采用三节点三角形单元,Case3和Case4采用六节点三角形单元,由表1可知,Case1和Case3的节点数一致,Case2和Case4的节点数一致。由于算例Case0结果的正确性已经得到验证,因此Case0的结果可作为参照。
由图7可知,Case1~Case4的压强分布与Case0基本一致,说明采用高阶单元时,虽然单元数目较少,但是可以得到较为准确的压强分布。
由表2可知,各算例的最大压强均与文献[2]较为接近,说明在网格数较少时,高阶单元也可以得到较准确的峰值压强;同时,Case3的反力大于Case1,Case4的反力大于Case2,且与参考值更接近;Case3的端泄流量和摩擦系数均小于Case1,与参考值较为接近,且Case4和Case2亦如此,说明节点数一样时,高阶单元计算得到的润滑结果更准确;由表3可知,Case3的内存和计算耗时均大于Case1,Case4的内存和计算耗时均大于Case2,但是Case3和Case4的计算误差更小,说明在节点数一致时,虽然高阶单元的单元数较少,但是精度更高。
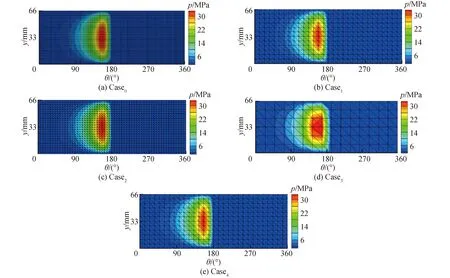
图7 不同算例压强分布对比Fig.7 Comparison of pressure distribution of different cases

表3 计算时间、内存及误差的对比Table 3 Comparison of calculation time, memory and error
3.3 实例计算
以某船用滑动轴承为例,采用六节点三角形单元和非结构格点型有限体积法研究轴承压强分布随倾角的变化规律,设定偏位角为0°,粘度为0.01 Pa·s,轴承半径为0.05 m,长度为0.2 m,间隙为0.04 mm,偏心率为0.6,转速为300 r/min。
由图8可知,随着倾斜角度的增加,轴承压强峰值逐渐向轴承的端部移动,同时轴承压强值逐渐增大,这是由于轴颈倾斜时,端部位置的油膜厚度急剧减小造成的。

图8 倾角对轴承压强分布的影响Fig.8 Effects of tilt angle on oil film pressure distribution
4 结论
1) 高阶单元对轴承压强分布和峰值压强的计算影响较小,但是会使油膜反力值更接近参考值。
2) 节点数一致时,高阶单元得出的端泄流量和摩擦系数更接近参考值。
3) 采用高阶单元时,滑动轴承液膜压强计算的精度会相应提高,但是内存消耗会相应增大,计算效率下降。
4)高阶单元模型可以适用于倾斜状态下的船用滑动轴承。
