熊晓婷，许学杰,李素文

(淮北师范大学物理与电子信息学院，安徽 淮北 235000)

0 引 言

奈奎斯特采样定理一直是信号处理领域的金科玉律，但面对当下海量数据信息的爆发式增长的形势，其性能的缺陷使信道容量、存储空间和计算机处理效率都面临巨大的挑战。进入二十一世纪后，数字信号处理理论得到了蓬勃的发展，压缩感知理论[1]的提出带来了颠覆性的改变，该理论以远小于奈奎斯特采样定理要求的采样密度对信号进行随机亚采样，通过远少于传统采样定理所需的数据量即可高精度重构原始信号。压缩感知强调从全局出发，把信号的采样和压缩阶段合二为一，这一特点避免了冗余信息的采集，节省了资源和时间，使其在全息成像、语音和通信等领域展现了强大的生命力和广泛的应用前景。

信号的重构算法设计是压缩感知最至关重要的技术，算法的优劣将直接影响重构质量的好坏，目前对重构算法的研究主要以贪婪算法为主，贪婪算法主要包括正交匹配追踪算法(OMP)[2]、正则化匹配追踪算法(ROMP)[3]、压缩采样匹配追踪算法(CoSaMP)[4]等。为了进一步获得更优秀的重构质量，对典型贪婪算法的改进势头愈发精益求精。徐志强等人引入随机支撑选择方法，比较迭代生成的概率值决定候选集，以此来减少广义正交匹配算法的运算量[5]；王丽等人提出了基于粒子群优化的快速正交匹配追踪算法，结合粒子群的局部选择最优的特点对算法匹配过程改进，进而降低了OMP的复杂度[6]；任晓奎等人在CoSaMP迭代中利用迭代次数与峰值信噪比的关系，自适应确定迭代次数，有效提高算法的效率[7]；杜秀丽等人提出了行间支撑集相似度的CoSaMP[8]。这些研究虽然提高了重构算法的性能，但仅仅针对单一信号进行实验验证，且提高精度有限，基于此提出了μCoSaMP算法，通过对数据域、图像域的多次仿真并结合绝对误差、成功重构概率和峰值信噪比综合评估，验证了改进算法具有更优的重构性能。

1 算法描述

1.1 压缩感知理论

压缩感知理论指出，只要信号是稀疏的或者在某一个变换域中是稀疏的,那么该信号就可以用一个观测矩阵来测量，将高维的稀疏信号降维成低维的观测信号，这就达到了压缩的目的，观测信号涵盖了稀疏信号最重要的信息，最后再求解一系列的最优化问题就能够以较高的精确度重构原始信号。

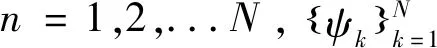
(1)

上式中，θ是信号x在ψ域中的表示，x和θ一一对应。若θ中有K个不为零或远大于零的系数，而剩下的N-K个系数为零或趋向于零，那么信号x在ψ域上就是K-稀疏的。其中ψ=[ψ1,ψ1,...,ψN]称为稀疏基。若信号要稀疏或近似稀疏表示，则需选择合适的正交或者非正交稀疏基。最常用的稀疏基有离散傅里叶变换基、离散余弦变换基等。因为离散余弦变换能把绝大多数的信息放置到很少的系数上，提高了编码效率，所以本文在图像稀疏化时选择离散余弦变换基作为稀疏基。

获得稀疏信号后，就要通过特别的方式采样。传统的采样方式是均匀采样获取数据，照顾不到全局信息，导致采样点之间的相关度高，存在信息冗余，而压缩感知是从数据的全局出发，通过计算信号与一个观测函数之间的内积来获得观测数据,观测数据中包含信号最重要的信息，保证了观测值之间的冗余度很低，所以观测点的数目要比奈奎斯特采样点数少的多，同时不影响信号高精度的恢复。具体地，假设x是ψ基下的K-稀疏N维信号，用一个与稀疏基不相关的观测矩阵Φ对该信号进行压缩观测：

y=Φx

(2)

上式中，原始信号x在采样过程被压缩成M维观测向量y，观测值y包含了原始信号的关键信息，Φ为观测矩阵，大小为M×N，Φ的每一行相当于一个传感器，它与信号x有关，用于获取信号的一部分信息。把(1)式代入(2)式得到：

y=Φx=Φψθ=Aθ

(3)

其中，A=Φψ称为传感矩阵。常见的观测矩阵有随机高斯矩阵、部分傅里叶矩阵和部分哈达玛矩阵等。基于随机高斯矩阵的特点和易实现性，本文压缩感知重构算法中的观测矩阵选择的是随机高斯矩阵。

得到观测值y后，从y中重构出信号x是解决一个线性方程的问题。显然，从(3)式可以看出，这是一个欠定方程。但已知压缩感知理论的约束条件是信号K-稀疏，同时矩阵A满足有限等距性质[9]，这就使信号重构成为可能，设计巧妙的观测矩阵Φ能够保证方程有唯一解，基于此，压缩感知重构信号的目标函数可以表达为：

(4)

式中，‖‖lp是p阶范数，压缩感知重构算法主要恢复有限维的信号，所以目前的重构算分为两类：一类是基于迭代的贪婪算法；一类是基于一阶范式最小化的凸优化算法。凸优化算法在很大程度上能提高重构精度，但计算复杂度高，不适合实际应用。贪婪迭代算法具有简单、快捷和复杂度低等优点而被广泛使用。

1.2 改进的重构算法

贪婪算法的思想是迭代地从稀疏基中选择合适的原子使其进行线性组合进而不断地逼近观测值。OMP算法是在MP算法的基础上改进的，ROMP算法又是在OMP算法改进的，其在每次迭代时选择多列，一定程度上提高重构效率。但正交匹配追踪算法和正则化正交匹配追踪算法在迭代时一旦选择某个原子，该原子会一直存在于索引集中，而在实际迭代过程中，并不能保证每次选择的原子都是准确无误的，如果某次选择出现错误，则在后续的迭代中该错误将无法得到修正，甚至造成累计错误，进而影响重构精度。为了解决该问题，顺势而生的CoSaMP算法在贪婪算法家族里崭露头角。

该算法的独到之处在于每次选择的原子可能在下一次迭代时被剔除，那么初选的错误原子就可以通过复选被淘汰，从而使得最终保留下来的原子集合高概率吻合于真实的支撑集。该算法的本质思想是：利用观测矩阵各列与残差的内积作为一个逼近原始信号x的“桥梁”，该“桥梁”的表达式如下：

ν=ΦTrt-1=〈ΦT,rt-1〉

(5)

CoSaMP算法在每次迭代时，都要向“桥梁”确定前K个最大的原子，以此来逼近原始信号。显然从(5)式可以看出，计算内积容易选择重复原子，也不能完全反映出“桥梁”要放大重要信息数据的能力，因此如何更优秀地选择匹配残差的原子，是进一步提高CoSaMP算法重构性能的重点。

基于上述问题，改进的CoSaMP算法在选择原子阶段，把“桥梁”ν引入相干性系数μ，其定义[10]如下：

(6)

其中p和q均为向量，pi表示向量p中的第i个元素，qi表示向量q中的第i个元素，(6)式利用p、q的每个元素来计算相干性，从而有效地帮助“桥梁”区分相干性较高的原子，确保初选原子候选集的正确率。同时，在算法剔除原子阶段，把信号和残差进行加权以获得最终的支撑集，确保选择和剔除原子的标准趋同，具体的算法流程如下：

步骤1：初始化r0=y，预估计信号稀疏度为K，Δ0=∅，Q=∅，t=1；

步骤2：计算“桥梁”ν=μΦTrt-1=μ〈ΦT,rt-1〉，μ是引入的相干性系数，选取ν中前2K个能量最大的元素，这些元素对应的列序号组成集合Q，合并Δt=Δt∪Q，按照对应的索引选取的原子组成支撑集ΦΔt；

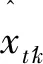
算法中的终止条件可以描述为下式：

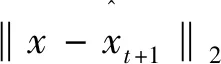
(7)

2 实验比较与性能分析

2.1 数据域的评估标准

1)绝对误差

在数学概念中绝对误差指的是测量值与真实值之差，其计算简单且具有正负方向性，但信号是一个矢量，无法直接比较大小，因此在估计算法重构信号误差时需要对绝对误差进行改进。首先得到误差向量：

(8)

δ=‖δ0‖2

(9)

δ值越小说明重构信号与原始信号之间的误差越小，重构效果越好。

2)成功重构概率

如果通过算法恢复的残差rt其二范数值小10-6则认为重构信号成功，成功次数记为P*，定义在有限次迭代次数下成功重构概率为：

(10)

式中，CNT为迭代次数。

2.2 图像域的评估标准

对于两幅质量差别较大的图像，人眼能够轻易的辨别出哪幅图像质量好哪副质量差。但当人眼无法分辨哪副图像更胜一筹时，可以把峰值信噪比PSNR作为评估重构图像质量的指标。峰值信噪比常通过均方误差(MSE)来定义：

(10)

其中，M×N为图像的尺寸，A(i,j)和B(i,j)表示图像重构前后的数据。PSNR常定义为：

(11)

上式中，max表示图像的最大像素值，PSNR的单位为dB，PSNR值越大，重构失真越小。

3 实验比较与性能分析

3.1 一维信号的重构结果

本实验选用rand()函数生成长度N=256的随机信号，观测值M=64，稀疏度K=12，迭代次数CNT=100，μCoSaMP算法与CoSaMP算法平均重构结果如图1所示。

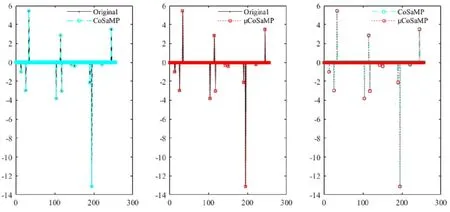
图1 μCoSaMP算法和CoSaMP算法平均重构结果

取迭代次数CNT=1000，稀疏度K分别取4、12，测量数与成功重构概率关系曲线如图2所示。

图2的横轴为测量点数，纵轴为信号成功重构概率。从图中可以看出，对于原始算法和改进算法，信号成功重建概率均随着观测点数的增加而增大。当K=4时，改进算法在M=30的成功重构概率接近1，而原始算法所需的观测点数至少需要40；当K=12时，改进算法在M=55的成功重构概率接近1，明显少于原始算法所需的观测点数；通过对比不同稀疏度下两种算法的成功重构概率发现，K=4的成功重构概率误差比K=12的要大很多，这意味着相对于原始算法，改进算法在K=4时的重构性能优越性更大。因此，改进算法成功重建信号的稳定性更强，且信号越稀疏，性能优势越明显。

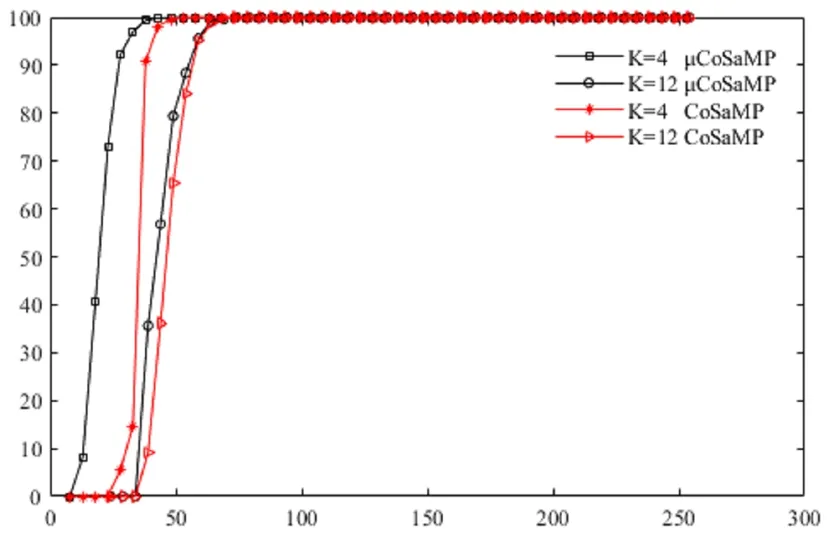
图2 测量数与成功重构概率关系曲线

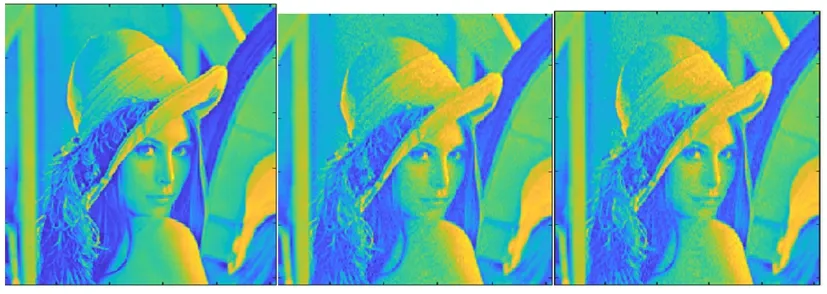
(a)原图 (b)μCoSaMP (c)CoSaMP

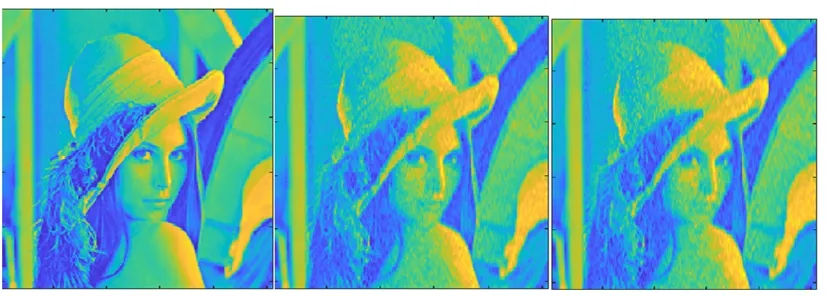
(a)原图 (b)μCoSaMP (c)CoSaMP

基于对平均重构结果和测量数与成功重构概率关系曲线的分析，改进的压缩采样匹配追踪算法在重构一维信号上具有重构精确度高和鲁棒性强的特点。

(a)原图 (b)μCoSaMP (c)CoSaMP

(a)原图 (b)μCoSaMP (c)CoSaMP

3.2 二维图像的重构结果

本实验先采用离散余弦变换基作稀疏处理，再采用随机高斯矩阵进行观测降维，最后采用CoSaMP算法和本文提出的μCoSaMP算法分别对Lena图像和Vegetables图像进行重构，比较两种算法在各采样率(M/N)下的PSNR值如表1所示。

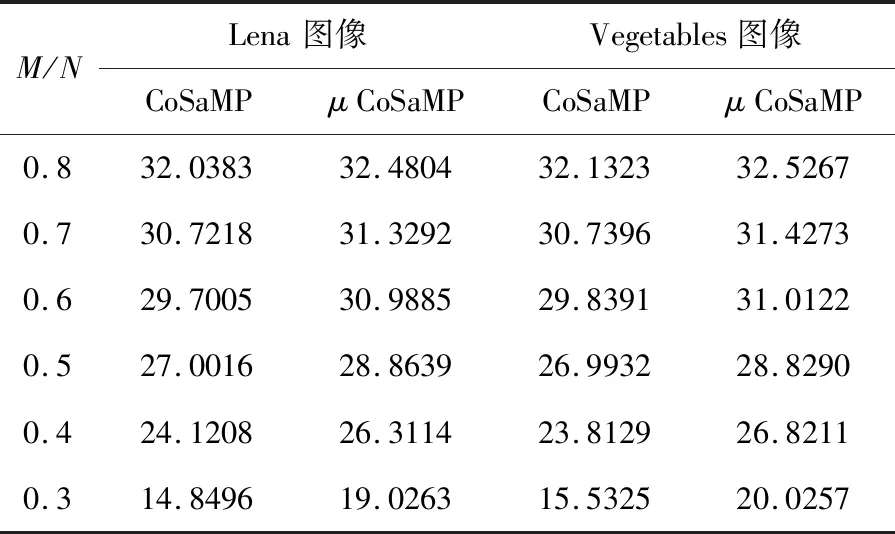
表1 不同采样率下图像重构的PSNR值比较

从表1的数据看出，虽然两种算法都能成功恢复实验图像，但是不论在何种采样率下μCoSaMP算法重构的PSNR值均不同程度的高于CoSaMP算法，当采样率为0.5或低于0.5时，这种差距更加明显。图3至图6分别为两幅实验图像在不同采样率下重构图像对比，以便直观地分析改进算法的重构优势。

从图3和图5中，能清晰地观察出在采样率为0.8下两种算法重构的图像失真小，图像细节纹理处无明显颗粒，帽沿线条和蔬菜轮廓清晰；但采样率降低为0.4时，从图4和图6中看到重构图像失真现象明显，相对于CoSaMP算法而言，改进算法的重构图像人物五官和蔬菜边缘的模糊程度要低。基于上述不同重构算法对二维图像重构质量的分析，低采样率下改进的压缩采样匹配追踪算法的重构效率更高，重构质量更优，避免了时间和硬件资源的浪费。

4 结 语

通过对压缩采样匹配追踪算法性能的分析，提出了μCoSaMP算法，选择原子阶段引入相干性系数，改变内积原则，提高初选原子准确率，同时提出在剔除原子阶段将信号和残差加权的思想，保证选择与剔除标准一致，准确估计支撑集。从对一维随机信号、二维图像的重构实验结果可以得出，μCoSaMP算法比CoSaMP算法在绝对误差、成功重构概率和峰值信噪比上都有较大的优势，因此μCoSaMP算法具有重构精确度高和鲁棒性强的特点。但值得思考的是，μCoSaMP算法也需要同CoSaMP算法一样把已知信号的稀疏度作为先验条件，在实际情况下往往无法预知信号的稀疏度，因此进一步的设计稀疏度自适应的μCoSaMP算法是接下来研究的重点内容。