非线性混杂随机泛函微分方程解的收敛性分析①
2020-10-29寇静
寇 静
(太原工业学院理学系,山西 太原 030008)
0 引 言
常微分方程作为数学模型的一种,在实际中已经被广泛应用于多个领域,例如汽车、航天、船舶、农业等[1]。为了更加精准地描述客观世界的变化规律,将时间滞后影响考虑在内,因而产生了泛函微分方程。泛函微分方程指的是定义在某个函数空间中的泛函,不但与自变量有关,还与某个时间段的状态相关,有效解决了常微分方程的应用局限性[2]。
在实际中,对常规的泛函微分方程进行优化与研究得到了随机泛函微分方程。随机泛函微分方程的应用范围较为广泛,其中,使用率最高、应用范围最广的类型为非线性混杂随机泛函微分方程[3]。但是在实际应用过程中发现,非线性混杂随机泛函微分方程解较为复杂,计算量过大,计算过程也非常冗长。由于现有的非线性混杂随机泛函微分方程解收敛性分析方法存在着均方稳定性较低的缺陷[4],在实际中的应用效果并不理想,因此为了解决上述问题,提出非线性混杂随机泛函微分方程解收敛性分析方法研究。
1 非线性混杂随机泛函微分方程解收敛性分析方法
1.1 构建非线性混杂随机泛函微分方程
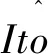
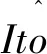
(1)
式(1)中,f表示的是漂移系数,f:Rn×[0,T]→R;g表示的是扩散系数,g:Rn×[0,T]→Mn×m;W(t)表示的是标准的Brown运动。f与g同时也能够表示该方程的精确解的参数。
将公式(1)转换为积分形式,表示如下:
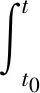
(2)
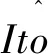
Stratonovich型的非线性混杂随机泛函微分方程表示为:
(3)
将公式(3)转换为积分形式,表示为:
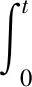
(4)
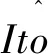
1.2 方程解计算
以上述构建的非线性混杂随机泛函微分方程为基础,采用截断E-M算法对该方程的解进行计算为下述方程解收敛性分析奠定基础[8]。
截断E-M算法是一类通过迭代进行极大似然估计的优化算法。该算法的标准计算框架由E步与M步交替构成,具有极强的收敛性,可以保障在迭代次数最少情况下达到局部极大值。截断E-M算法中的迭代规则可以灵活精准地获得隐变量,由于这一优点,该算法已经被应用于多个领域[9]。
截断E-M算法具有三个假设条件,具体如下所示。
假设一:若系数f与g满足局部Lipschitz条件,对于任意的R>0,存在KR>0,得到|f(φ)-f(ψ)|∨|g(φ)-g(ψ)|KR‖φ-ψ‖,其中,φ,ψ∈C([-τ,0];Rn)。
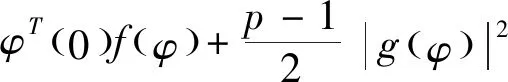
假设三:对于t,s∈[-τ,0],存在常数K0>0,得到|ξ(t)-ξ(s)|2K0|t-s|。
假定非线性混杂随机泛函微分方程解存在并具有唯一性。若该方程同时满足假设条件一与假设条件二,则方程(即公式(1))具有唯一的全局解X(t)[10]。
若方程只满足假设条件二,则方程具有两个解,表示为:
(5)
1.3 方程的p阶有界性分析
以上述求得的非线性混杂随机泛函微分方程解为依据,分析方程的p阶有界性[11]。
方程的p阶有界性指的是非线性混杂随机泛函微分方程具有上界与下界,能够进一步证明方程解的唯一性。
若方程均满足假设条件一、假设条件二与假设条件三,对于任意p≥2,方程边界为:
(6)
式(6)中,X(t)max表示的是方程的上界;X(t)min表示的是方程的下界。
非线性混杂随机泛函微分方程的p阶有界性如图1所示。
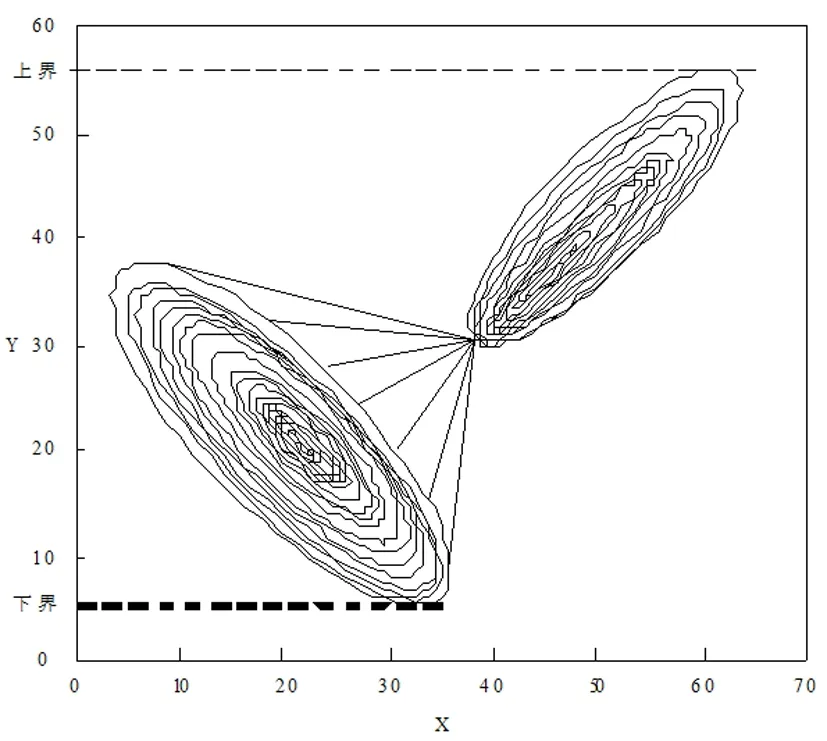
图1 非线性混杂随机泛函微分方程的p阶有界性示意图
如图1所示,非线性混杂随机泛函微分方程具有p阶有界性,表明该方程具有唯一解,即为X(t),通过该结果能够为下述方程解收敛性证明提供依据[12-13]。
1.4 方程解的收敛性证明
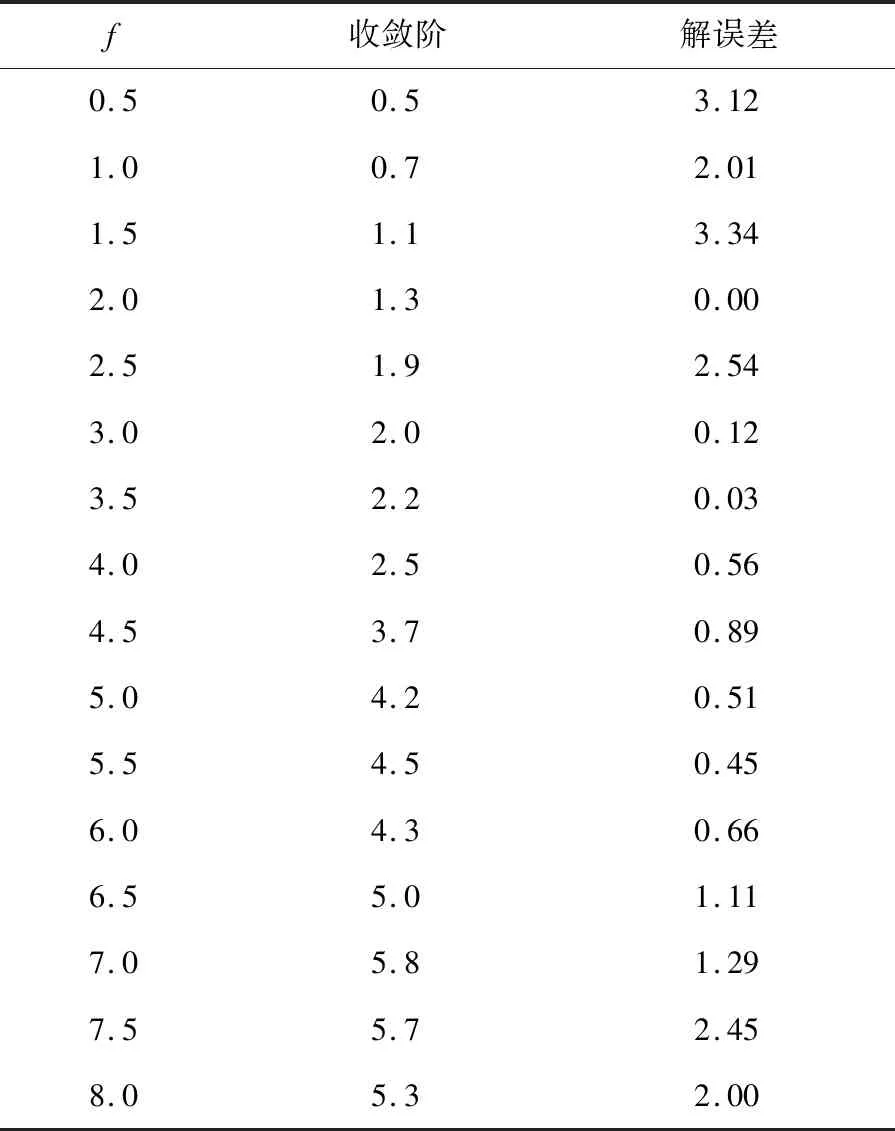
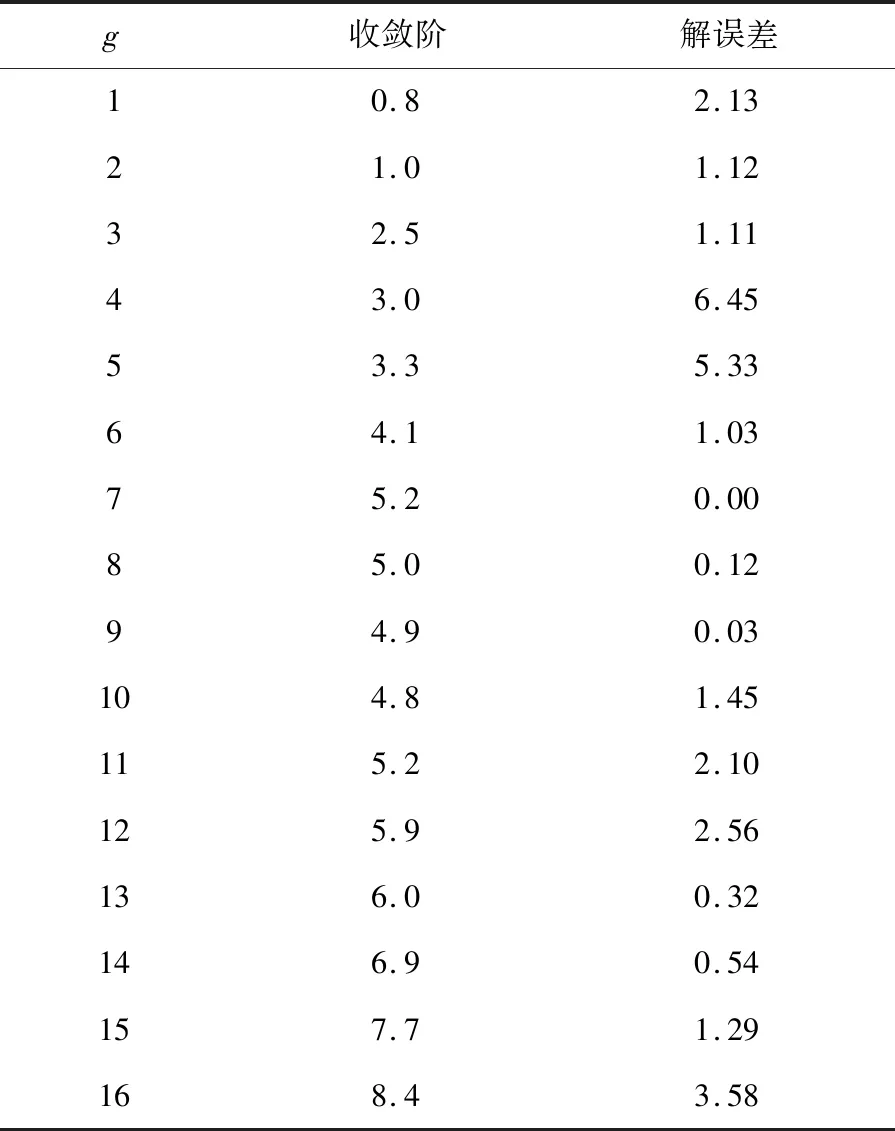
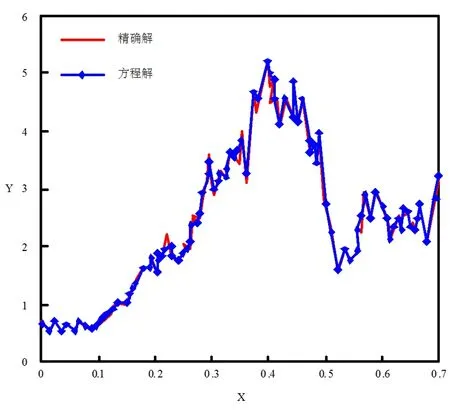
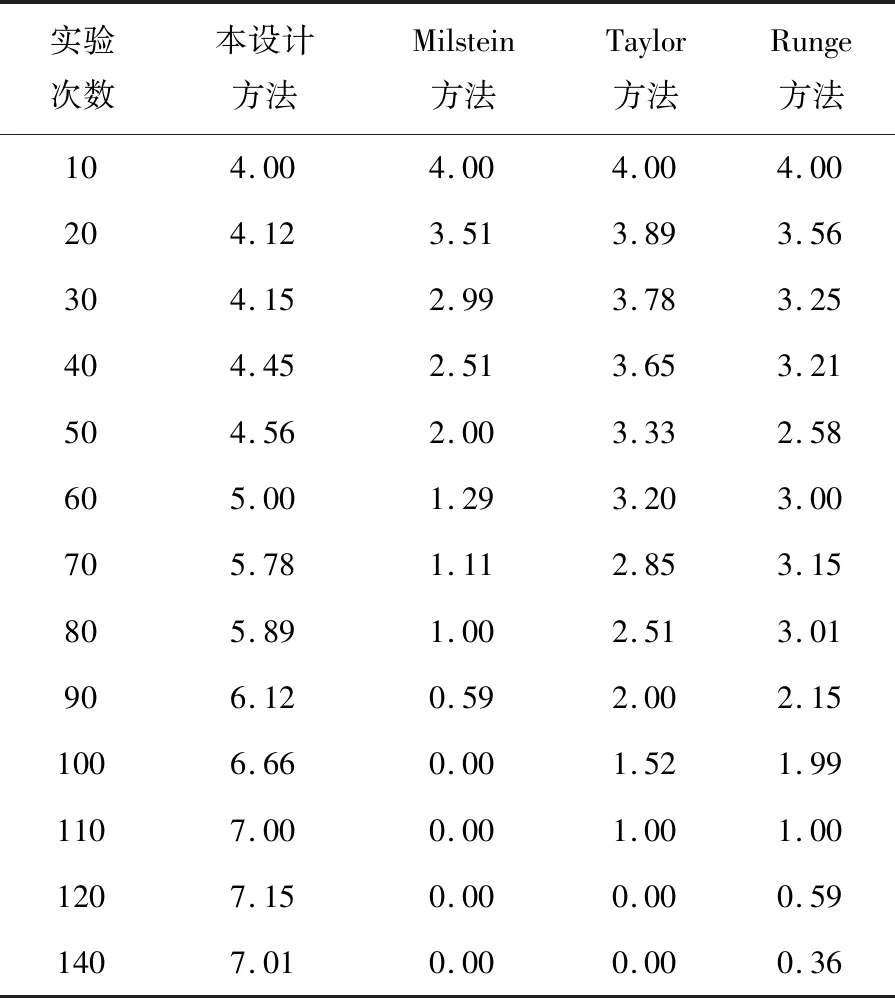
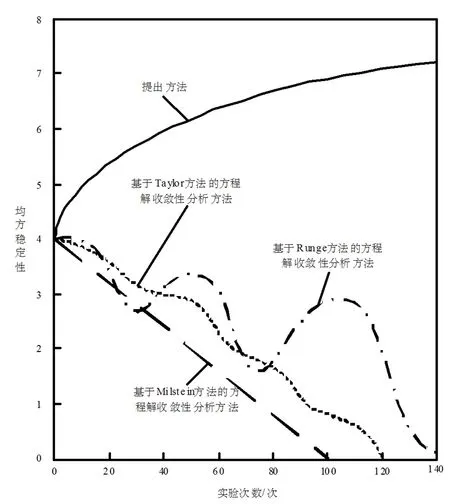
非线性混杂随机泛函微分方程解收敛性证明,指的是在T>0,2q (7) 为了证明公式(7)成立,需要引入下述定理。 定理一:若该方程只满足假设条件一[14-15],存在R>‖ξ‖,定义停时τR=inf{t≥0:‖X(t)‖≥R}。 定理二:若该方程同时满足假设条件一与假设条件二,存在R>‖ξ‖与Δ∈(0,Δ*],定义停时τΔ,R=inf{t≥0:‖X(Δ,t)‖≥R}。 (8) 对公式(8)进行整理,得到非线性混杂随机泛函微分方程解的收敛性证明公式,表示为: (9) 至此,通过上述过程实现了非线性混杂随机泛函微分方程解的收敛性证明与分析。 上述过程完成了非线性混杂随机泛函微分方程解收敛性分析方法的设计,但是无法确定该方法的实际应用性能,为此设计仿真对比测试。 在仿真对比测试中,采用现有的使用较为广泛的三种方法,即基于Milstein方法的非线性混杂随机泛函微分方程解收敛性分析方法、基于Taylor方法的非线性混杂随机泛函微分方程解收敛性分析方法以及基于Runge方法的非线性混杂随机泛函微分方程解收敛性分析方法,与提出方法进行对比测试,通过均方稳定性验证本文所设计方法的实际应用性能。常规情况下,均方稳定性越高,则方法的分析性能越好,反之,则方法的分析性能越差。 以公式(1)非线性混杂随机泛函微分方程为实验对象,为了使方程得到唯一的精确解,进而保证测试数据的准确性,首要的任务就是确定实验对象方程的精确解参数f与g。 在此次实验中,本文主要采用试值方法确定方程精确解参数,试值具体数据如表1与表2所示。 表1 方程精确解参数f 表2 方程精确解参数g 如表1、表2所示,当误差为0.00时,该参数即为方程精确解的最佳参数,也就是说,当f为2.0,g为7时,方程解最接近精确解,具体情况如图2所示。 图2 方程解与精确解对比图 将上述确定的方程的最佳参数值代入公式(1)中,以此为基础,进行均方稳定性测,其中,测试数据如表3所示。 表3 测试数据表 将表3测试数据输入到MATLAB软件中,经过轨道计算,多次迭代,得到均方稳定性对比情况如图3所示。 分析图3可知,本设计方法的均方稳定性远远高于现有三种方法,充分说明提出的非线性混杂随机泛函微分方程解收敛性分析方法具备更好的收敛性分析性能,实际应用性能更优。 图3 均方稳定性对比情况图 针对传统方法均方稳定性差的问题,本文提出了非线性混杂随机泛函微分方程解收敛性分析方法,经实验证明,该方法极大地提升了均方稳定性,为方程解收敛性分析方法的进一步发展提供了新思路,综合实用性强。但是,在分析过程中发现,本文提出方法计算出来的方程解依然与精确解具有些许的误差,为此,需要对提出的非线性混杂随机泛函微分方程解收敛性分析方法进行进一步的优化研究,以期降低计算误差,提升方程解的精准度。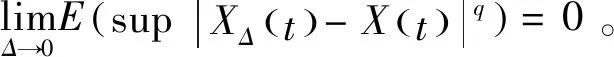
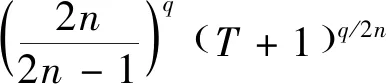
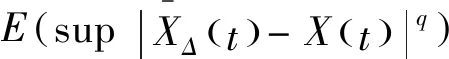
2 均方稳定性测试
2.1 确定方程精确解
2.2 均方稳定性分析
3 结 语
