王静，曹小红

（陕西师范大学 数学与信息科学学院， 陕西 西安710062）

0 引 言

文中，H 表示无限维复可分的Hilbert 空间，B(H )为H 上的有界线性算子的全体，T*表示T ∈B(H )的共轭算子。若T 的值域R(T )为闭集且其零空间N(T )是有限维的，称算子T ∈B(H )为上半Fredholm 算子；若值域R(T )的余维数有限，则称T ∈B(H )为下半Fredholm 算子。如果T 既为上半Fredholm 算子又为下半Fredholm 算子，则称T ∈B(H )为Fredholm 算子。对半Fredholm 算子T( 上 半 或 者 下 半)，令n(T )=dimN(T ),d(T )=dim(H/R(T )), 其指标定义为ind(T )=n(T )-d(T )。 算 子T ∈B(H ) 的 升 标asc(T ) 为 满 足N(Tn)=N(Tn+1)的最小正整数n，若这样的正整数不存在，则记asc(T )=+∞;而T ∈B(H )的降标des(T )为满足R(Tn)=R(Tn+1)的最小正整数n，若这样的正整数不存在，则记des(T )=+∞。若T 是指标为零的Fredholm 算子，则称T 为Weyl 算子；若T 是有有限升降标的Fredholm 算子，则称T 为Browder 算子。如果T 为上半Fredholm 算子且n(T )=0，则 称 T ∈B(H ) 为 下 有 界 算 子σ(T ),σe(T ),σw(T ),σb(T ),σa(T ),σea(T ),σab(T ),σp(T ),σSF+(T ),σSF-(T )分别表示T 的 谱、本 质谱、Weyl 谱、Browder 谱、逼近点谱、本质逼近点谱、Browder 逼近点谱、点谱、上半Fredholm 谱和下半Fredholm 谱，并记

对集合E⊆C，用isoE表示E中孤立点的全体，accE表 示E中 聚 点 的 全 体。 如 果isoσ(T )⊆σp(T ),则称T 为isoloid 算子。

Weyl 定理最初由WEYL[1]在研究自伴算子T 的谱时发现，近年来，国内外许多学者开始研究满足Weyl 定理的算子，于是满足Weyl 定理算子的范围不 断 扩 大[2-9]。如 果σ(T )σw(T )=π00(T ), 其 中，π00(T )={λ∈isoσ(T ): 0 ＜n(T -λI)＜∞},则 称算子T ∈B(H )满足Weyl 定理。HARTE 等[10]对Weyl 定理进行了变形，变形后的Weyl 定理被定义为Browder 定理,即算子T 满足

若T ∈B(H ) 满 足N(T -λI)⊆[(T -λI)n]}, 则 称T 为Saphar 算 子[11]，用σS(T ) 表 示Sapher 谱。GOLDBERG[12]定义了一个新的谱集σG(T ) ={λ∈C:T -λI值域非闭集}， 此 时 有σK(T )=σS(T )∪σG(T )[13]。近年来，对Weyl 定理相关问题的研究备受关注，已得到许多好的结果。本文继续该研究，给出Weyl 定理新的判定方法。

1 主要结论及证明

首先，定义一个新的集合，令

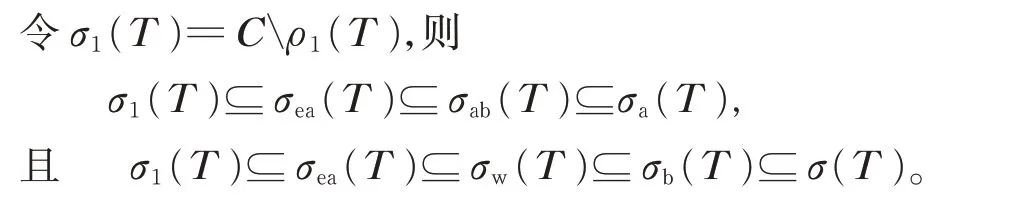
下面讨论算子的Browder 定理。

定理1设T∈B(H ),则下列叙述等价:

(1)T 满足Browder 定理;

证明(1)⇒(2)。

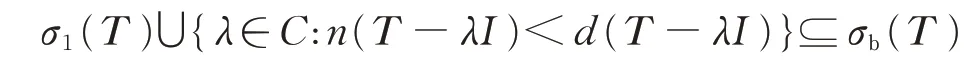
显然成立。

下证

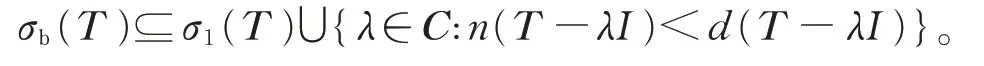
对任给的λ0∉σ1(T )，有n(T -λ0I) ＜∞,存在ε＞0，当0 ＜|μ-λ0|＜ε时，μ∉σea(T )，并且

T -λ0I为Fredholm 算子。由Fredholm 算子的摄动定理可知，

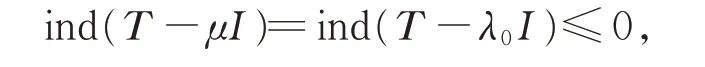
所以ind(T -λ0I)=0,λ0∈ρw(T )=ρb(T )。

(2)⇒(3)。只 需 证σ(T )⊆σb(T)∪σS(T )。 由文献[14]知，σ0(T )⊆σS(T ),于是

下证σb(T )⊆σw(T )。对任意的λ0∉σw(T )，由Fredholm 算 子 摄 动 定 理 知，存 在ε＞0, 当0 ＜|μ-λ0|＜ε时，μ∉σ1(T )∪{λ∈C:n(T -λI)＜d(T -λI)}∪σS(T ),即T -μI可 逆，于 是λ0∉σb(T )，因 此T 满 足Browder 定理。

注解1在定理1 中，当T满足Browder 定理时，σb(T )分解的两部分缺一不可。

例1T ∈B(l2),令

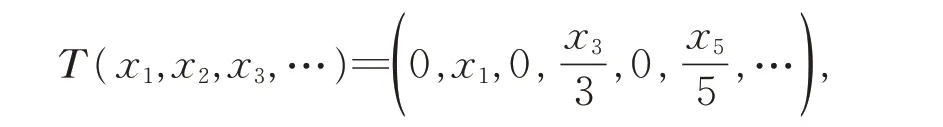
则σ(T ) =σw(T ) =σb(T ) = {0}, 即 T 满 足Browder 定理。但由于

例2T ∈B(l2),令

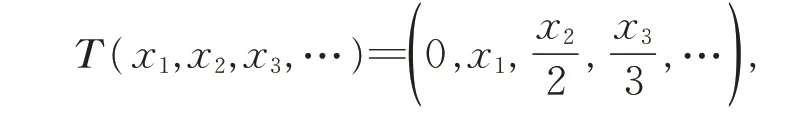
则σ(T )=σw(T )=σb(T )= {0}, 即 T 满 足Browder 定 理 。 但 由 于σ1(T )=ϕ, 故σb(T )≠σ1(T )。

注解2在定理1 中，当T 满足Browder 定理时，σ(T )分解的三部分缺一不可。

例3T ∈B(l2)，令

则σ(T ) =σw(T ) =σb(T )= {λ∈C: |λ|≤1}，说 明T 满 足Browder 定 理。由 于{λ∈C:n(T -λI)＜d(T -λI)}=ϕ,σS(T )⊆{λ∈C:|λ|=1},故σ(T )≠{λ∈C:n(T -λI)＜d(T -λI)}∪σS(T )。

例4T ∈B(l2)，令

则σ(T )=σw(T )=σb(T )= {0}, 即 T 满 足Browder 定 理 。 由 于σS(T )=ϕ, 故σ(T )≠σ1(T )∪σS(T )。

例5T ∈B(l2)，令

则σ(T )={0,1},σb(T )=σw(T )={1},说明T 满足Browder 定理。由于

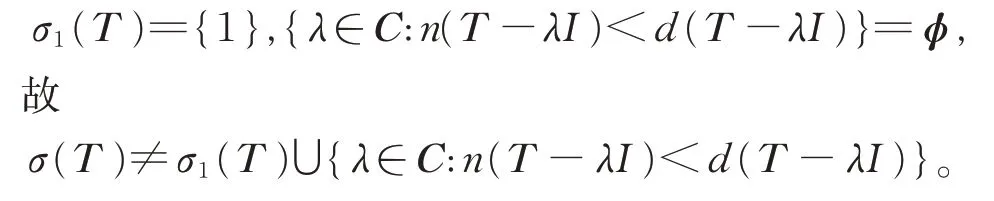
注解3设T ∈B(H)，则下列叙述等价

(i)σb(T )=σ1(T );

(ii)σea(T )=σw(T ),T 为isoloid 算子且满足Weyl定理；

证明(i)⇒(ii) 。 由 于σ1(T ) ⊆σea(T ) ⊆σw(T ) ⊆σb(T )且σb(T )=σ1(T ), 则σea(T )=σw(T )=σb(T ), 故T 满 足Browder 定 理。 又 因π00(T )∩σ1(T )=ϕ,则π00(T )∪[σ(T )σw(T )]⊆ρb(T ),因此T 满足Weyl 定理。

下 证T 为isoloid 算 子。由 于{λ∈isoσ(T ):n(T -λI)=0}⊆ρ1(T )=ρb(T )， 可 证 得{λ∈isoσ(T ):n(T -λI)=0}=ϕ, 即T 为isoloid算子。

(ii)⇒(iii)。显然accσ(T )∪{λ∈C:n(T -λI)=∞}⊆σb(T )=σw(T )=σea(T )。

下证反包含关系成立。

对任意的

可得λ0∈isoσ(T )∪ρ(T )且n(T -λ0I)＜∞。不妨设λ0∈isoσ(T ), 由 于 T 为 isoloid 算 子, 则0 ＜n(T-λ0I)＜∞。 由T 满 足Weyl 定 理 知，λ0∈σ(T )σw(T )，即λ0∉σea(T )。

(iii)⇒(i)。σ1(T )⊆σb(T )显然成立。

下 证σb(T )⊆σ1(T )。 对 任 意 的λ0∉σ1(T ),n(T -λ0I)＜∞, 存 在ε＞0, 当 0 ＜|μ-λ0| ＜ε时,μ∈ρea(T ) 且 T -μI为 Saphar 算 子 , 则μ∉accσ(T )∪{λ∈C:n(T -λI)=∞}, 进 而μ∈isoσ(T )∪ρ(T ),n(T -μI)＜∞。

又 因 T -μI为 上 半 Fredholm 算 子, 则μ∉σb(T )。由于T -μI为Saphar 算子，由定理1 中(2) ⇒ (3) 的 过 程 ，得μ∈ρ(T ), 进 而 有λ0∈isoσ(T )∪ρ(T )。 由 于λ0∉{λ∈C:n(T -λI)=∞},因此λ0∉σea(T ),λ0∉σb(T )。

注 解 4若 对 任 意 多 项 式p，都 有p(σ1(T ))⊆σ1(p(T ))，则对任意的λ，μ∈ρe(T )，有ind(T -λI)ind(T -μI)≥0。

证明反证法。假设存在λ0,μ0∈ρe(T ),使得

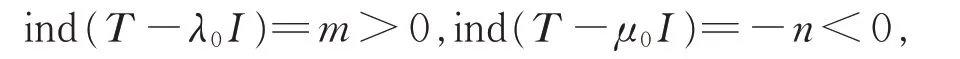
其中m,n为正整数。令p(T )=(T -λ0I)n(T -μ0I)m+1,p(λ0)=p(μ0)=0，p(T ) 为 Fredholm 算 子 且 indp(T )=-n＜0，0 ∉σ1(p(T ))。 又 因λ0∈σ1(T ), 此 时 0=p(λ0)∈p(σ1(T ))⊆σ1(p(T )),矛盾。因此，对任意的λ,μ∈ρe(T ),ind(T-λI)ind(T -μI)≥0。

由文献[15]，对任意的λ,μ∈ρSF+(T ),ind(T -λI)ind(T -μI)≥0 当且仅当对任意多项式p，都有

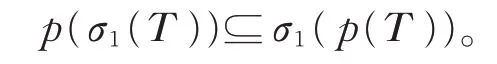
注 解5若σea(T )=accσ(T )∪{λ∈C:n(T -λI)=∞},则对任意多项式p，p(T )满足Browder 定理且p(σ1(T ))⊆σ1(p(T ))。

注解6若T 满足Browder 定理，则对任意多项式p，p(T )满足Browder 定理当且仅当对任意的λ,μ∈ρe(T ),ind(T -λI)ind(T -μI)≥0。

注 解 7设 T 满 足 Browder 定 理，若σ1(T )⊆σe(T ) 或 对 任 意 多 项 式p，p(σ1(T ))⊆σ1(p(T )) 成 立，则 对 任 意 多 项 式p，p(T )满足Browder 定理,但逆命题不成立。

例6A,B,C,D ∈B(l2)，分别令

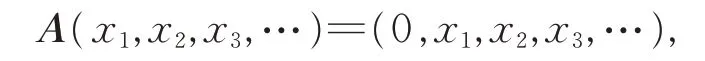
(2) 对 任 意 的λ∈ρe(T ), 有λ∈{λ∈C:|λ|≤1}∪ρ(T ), 即 ind(T -λI)=1或ind(T -λI)=0。 于是对任意多项式p，p(T )满足Browder 定理；

(3)σ1(T )={λ∈C:|λ|≤1}∪{λ∈C:|λ+2|≤1},σe(T )={λ∈C:|λ-2|≤1}∪{λ∈C:|λ+2|≤1},

故σ1(T )⊆σe(T )不成立；

(4) 设p0(T )=T(T -2I),由T 为Fredholm 算子, ind(T )=1,T -2I为上半Fredholm 算子,d(T -2I)=∞，知p0(T )为上半Fredholm 算子且p0(T )＜0, 故 0 ∉σ1(p0(T )), 但 0=p0(T )，而0 ∈σ1(T ),即0 ∈p0(σ1(T ))。故存在多项式p0(T )，使得p0(σ1(T ))⊆σ1(p0(T ))不成立。

下面利用σ1(T )给出算子函数满足Browder 定理的充要条件。

定理2设T ∈B(H )满足Browder 定理，则对任意多项式p，p(T )满足Browder 定理当且仅当下列条件之一成立：

(1)σ1(T∗)⊆σe(T∗)；

(2)对任意多项式p，p(σ1(T ))⊆σ1(p(T ))。

证明必要性。 假设(1)不成立,则存在λ0∈σ1(T∗)σe(T∗), 于 是ind(T∗-λ0I)＞0, 即 存在λ0∈ρe(T ),使得ind(T -λ0I)＜0。因而对任意的μ∈ρe(T ),ind(T -μI)≤0。 对 任 意 多 项 式p,设μ0∉σ1(p(T )),令

当|λ-λ1| 充 分 小 时,p(T )-p(λ)I 为 上 半Fredholm 算子且ind(p(T )-p(λ)I)≤0,从而T -λI 为 上 半Fredholm 算 子 且ind(T -λI)≤0。 又 因p(T )-p(λ)I是 Saphar 算 子 ， 因 此p(λ)∉σK(p(T ))=p(σK(T ))[16]，即λ∉σK(T ), 则λ1∉σ1(T )。同理可证对1≤i≤k,都有λi∉σ1(T ),故对任意多项式p，p(σ1(T ))⊆σ1(p(T ))。

充分性。假设(1)成立，则对任意的λ∈ρe(T∗),有ind(T∗-λI)≤0, 即 对 任 意 的λ∈ρe(T ), 有ind(T -λI)≥0。 于 是p(T )满 足Browder 定理。若(2)成 立，由 注 解1～注 解7 可 知，p(T ) 满 足Browder 定理。

注 解 8（1） 若 对 任 意 的λ∈ρe(T ),ind(T -λI)≤0, 则 对 任 意 多 项 式p，有p(σ1(T ))⊆σ1(p(T ))。

（2）若 对 任 意 多 项 式p，p(σ1(T ))⊆σ1(p(T ))∪acc{μ∈C：n(p(T )-μI)＜d(p(T ) -μI)}，则 对任意的λ，μ∈ρe(T )，有ind(T -λI)ind(T -μI)≥0。

事实上,假设存在λ0,μ0∈ρe(T ),使得ind(T-

则 0 ∉p(σ1(T )),λ0∉σ1(T ),ind(T -λ0I)≤0,矛盾。故对任意的λ,μ∈ρe(T ),有

ind(T -λI)ind(T -μI)≥0。

由注解8 可得推论1～推论4。

推论1设T∈B(H )满足Browder 定理，若对任 意 多 项 式p，均 有p(σ1(T ))⊆σ1(p(T )) ∪acc{μ∈C:n(p(T )-μI)＜d(p(T )-μI)}当 且 仅当p(T )满足Browder 定理。

由定理2 的证明可知,若σ1(T∗)⊆σe(T∗)不成立，则存在λ0∈ρe(T ),使得ind(T -λ0I)＜0。于是当对任意多项式p，p(T )满足Browder 定理时，对任给λ∈ρe(T ),ind(T -λI)≤0,有：

推论2设T ∈B(H )满足Browder 定理，则对任意多项式p，p(T )满足Browder 定理当且仅当下列条件之一成立:

(1)σ1(T )⊆σe(T )；

(2)σ1(T∗)⊆σe(T∗)。

推论3设T ∈B(H )满足Browder 定理，且{λ∈ρe(T ):ind(T -λI)＜0}≠ϕ,则对任意多项式p，p(T ) 满 足 Browder 定 理 当 且 仅 当p(σ1(T ))⊆σ1(p(T ))。

证明由于{λ∈ρe(T ):ind(T -λI)＜0}≠ϕ,则 存 在λ0∈ρe(T ), 使 得ind(T -λ0I)＜0, 因 此λ0∈σ1(T∗)σe(T∗)，故σ1(T∗)⊆σe(T∗)不成立，由定理2，可知推论3 成立。

在 推 论3 中,条 件{λ∈ρe(T ):ind(T -λI)＜0}≠ϕ为本质的。

例7A,B ∈B(l2)，分别令

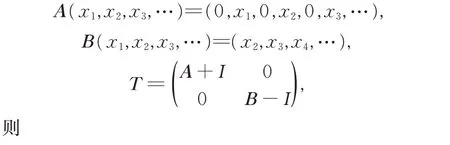
(1)σ(T )=σw(T )=σb(T )={λ∈C:|λ+1|≤1}∪{λ∈C:|λ-1|≤1},T 满足Browder 定理；

(2) 对 任 意 的λ∈ρe(T ),ind(T -λI)=0 或 者ind(T -λI)=1, 对 任 意 多 项 式p，p(T ) 满 足Browder 定理；

(3)设p0(T )=(T -I)(T +I),则0 ∉σ1(p(T )),但 由 于-1∈σ1(T )，而0=p0(-1)⊆p0(σ1(T ))。故存在多项式p0，使得p0(σ1(T ))⊆σ1(p0(T ))不成立。

相反，若T 满足Browder 定理，则对任意多项式p，由p(σ1(T ))⊆σ1(p(T ))并不能推出{λ∈ρe(T ):ind(T -λI)＜0}≠ϕ。

例8T ∈B(l2),令

则σ(T )=σw(T )=σb(T )={λ∈C:|λ|≤1},T 满 足 Browder 定 理 且 对 任 意 多 项 式p，p(σ1(T ))⊆σ1(p(T )), 但 {λ∈ρe(T ):ind(T -λI)＜0}=ϕ。

推论4设T ∈B(H )满足Browder 定理,则对任意多项式p,p(σ1(T ))⊆σ1(p(T ))当且仅当p(T )满足Browder 定理且下列条件之一成立：

(1)σSF+(T )=σe(T )；

(2)σe(T )=σw(T )；

(3){λ∈ρe(T ):ind(T -λI)＜0}≠ϕ。

证明必要性。 设对任意多项式p,p(σ1(T ))⊆σ1(p(T ))均成立，由定理2 知，p(T )满足 Browder 定 理。 若(1) 不 成 立，则 存 在λ0∈ρSF+(T ),使得ind(T -λ0I)＜0, 由 注 解6 可知，对任意的λ∈ρSF+(T ),均有ind(T -λI)≤0,即对任意的λ∈ρe(T ),ind(T -λI)≤0,若(2)不成立，则存在λ1∈ρe(T ),ind(T -λ1I)＜0,因此

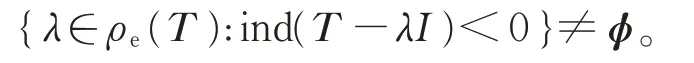
充分性。若(1)成立，由于对任意多项式p，p(T ) 都 满 足Browder 定 理，则 对 任 意 的λ,μ∈ρe(T ),ind(T -λI)ind(T -μI)≥0,即对任意的λ,μ∈ρSF+(T ),ind(T -λI)ind(T -μI)≥0。 于 是结论成立。

若(2)成立，可推断对任意的λ∈ρSF+(T ),ind(T -λI)≤0。事实上，若存在λ0∈ρSF+(T ), 使得ind(T -λ0I)＞0, 即 存 在λ0∈ρe(T )=ρw(T ),矛盾。于是充分性得证。

若(3)成立，由推论3 可知结论成立。

上面讨论了算子及算子函数的Browder 定理，下面考虑算子及算子函数的Weyl 定理。在定理1条件下，只能推出算子满足Browder 定理，无法推出该算子满足Weyl 定理。

例9T ∈B(l2),令

则T 满足定理1 的条件，于是T 满足Browder 定理，但通过计算，T 不满足Weyl 定理。

容易证得:

引理1设T ∈B(H ),p为一多项式，则

(1)isoσ(p(T ))⊆p(isoσ(T )∪ρ(T ))；

(2) 当T 为isoloid 算 子 且 满 足Weyl 定 理 时，p(T )为isoloid算子且

下面给出T 满足Weyl 定理的充要条件。

定理3设T ∈B(H ),则T 为isoloid 算子且满足Weyl 定 理 当 且 仅 当σb(T )=σ1(T )∪[{λ∈C:n(T-λI)＜d(T-λI)}∩accσ(T )]。

证明必要性。设T满足Weyl定理，由定理1知，

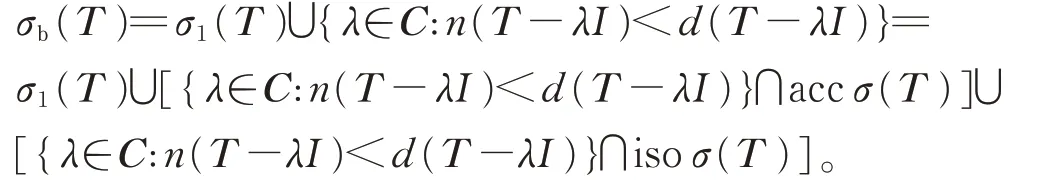
由T 为isoloid 算 子 且 满 足Weyl 定 理 知，{λ∈C:

可知π00(T )⊆ρb(T )，所以T满足Weyl 定理。

下证T为isoloid 算子。显然

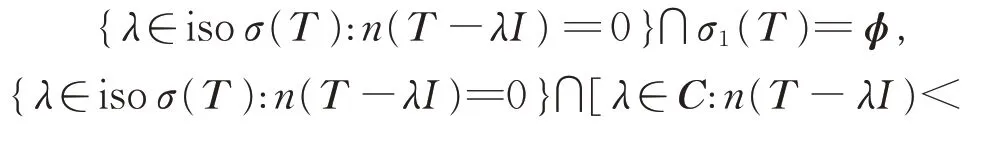
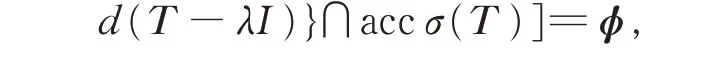
因此{λ∈isoσ(T):n(T -λI) =0}⊆ρb(T )。进而{λ∈isoσ(T ):n(T -λI)=0}⊆ρ(T )。 因 此{λ∈isoσ(T ):n(T -λI)=0}=ϕ, 则T 为isoloid算子。

注解9在定理3 中，条件“T 为isoloid 算子”是本质的。

例10T ∈B(l2)，令

则T 满足Weyl 定理但不为isoloid 算子。此时

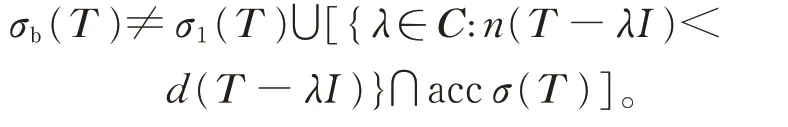
注解10在定理3 中，若T 为isoloid 算子且满足Weyl 定理，σb(T )分解的两部分缺一不可。

例11T ∈B(l2)，令

则σ(T )=σw(T )=σb(T )=σ1(T )={λ∈C:|λ|≤1},π00(T )=ϕ,可见T 满足Weyl 定理且为isoloid 算子。由于σ1(T )={λ∈C:|λ|=1}，故σb(T )≠σ1(T )。

例12T ∈B(l2)，令

注 解 11设 T ∈B(H )， 若{λ∈C：n(T -λI)＜d(T -λI)}=ϕ，则 下 列 叙 述等价：

(i)T 为isoloid 算子 且满足Weyl 定理；

(ii)σb(T )=σ1(T )；

(iii)对任意多项式p，p(T )为isoloid 算子且满足Weyl 定理。

下面讨论算子函数的Weyl 定理及σ1(T )的谱映射定理。由于iso σ(p(T ))=p(iso σ(T )∪ρ(T )),于是由定理2 及其推论，可得:

定理4设T ∈B(H )为isoloid 算子且满足Weyl 定理，则对任意多项式p，p(T )为isoloid 算子且满足Weyl 定理当且仅当下列条件之一成立:

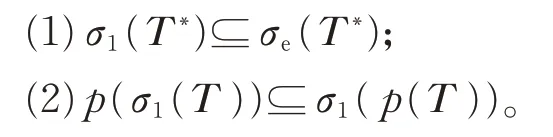
由推论1～推论4，可得推论5～推论10。

推论5设T ∈B(H )为isoloid 算子且满足Weyl 定 理 ，若 对 任 意 多 项 式p，都 有p(σ1(T ))⊆σ1(p(T )) ∪acc{μ∈C:n(p(T )-μI)＜d(p(T ) -μI)}当且仅当p(T )为isoloid 算子且满足Weyl 定理。

推论6设T ∈B(H )为isoloid 算子且满足Weyl 定理，则对任意多项式p，p(T )为isoloid 算子且满足Weyl 定理当且仅当下列条件之一成立:

(1)σ1(T )⊆σe(T )；

(2)σ1(T∗)⊆σe(T∗)。

推论7设T ∈B(H )为isoloid 算子且满足Weyl 定理，且{λ∈ρe(T ):ind(T -λI)＜0}≠ϕ,则对任意多项式p，p(T )为isoloid 算子且满足Weyl 定理当且仅当p(σ1(T ))⊆σ1(p(T ))。

推论8设T ∈B(H )为isoloid 算子且满足Weyl 定 理 ， 则 对 任 意 多 项 式p，p(σ1(T ))⊆σ1(p(T ))当且仅当p(T )为isoloid 算子且满足Weyl 定理且下列条件之一成立:

(1)σSF+(T )=σe(T )；

(2)σe(T )=σw(T )；

(3){λ∈ρe(T ):ind(T -λI)＜0}≠ϕ。

注解12设T 为isoloid 算子且满足Weyl 定理，则σ1(T )≠ϕ。

事实上，若σ1(T )=ϕ。此时可断言:intσ(T )=ϕ。假设intσ(T )≠ϕ,则存在连续线段L⊆∂σ(T )。取λ0∈L，由λ0∈ρ1(T )知，存在μ0∈B(λ0;ε)∩L，使得T -μ0I为上半Fredholm 算子且为Saphar 算子，又由于μ0∈∂σ(T )，从而有μ0∈ρ(T ),与μ0∈L⊆σ(T )矛盾。

由intσ(T )=ϕ，知σ(T ) =∂σ(T )。对任意的λ0∈σ(T )，由λ0∈ρ1(T )，可知λ0∈iso σ(T )，又由T为isoloid 算子，可得λ0∈σ(T )σb(T )。这就证明了σb(T )=ϕ,矛盾。

注 解13当intσ1(T )∩ρSF+(T )=ϕ 时，对任意 的λ∈ρSF+(T ),ind(T -λI)≤0。 于 是 当T 为isoloid 算 子 且 满 足 Weyl 定 理 时 ，若intσ1(T )∩ρSF+(T )=ϕ,则对任意多项式p，p(T )为isoloid 算子且满足Weyl 定理。但当对任意多项式p，p(T )为isoloid 算子且满足Weyl 定理时，无法推 出intσ1(T )∩ρSF+(T )=ϕ。 如 例12 中 的 算 子T，对任意多项式p，p(T )为isoloid 算子且满足Weyl定理，但intσ1(T )∩ρSF+(T )=ϕ。

定理5设T ∈B(H )为isoloid 算子且满足Weyl 定理。若σSF+(T ) =σe(T )，则对任意多项式p，p(T )为isoloid 算子且满足Weyl 定理当且仅当下列条件之一成立:

(1)intσ1(T )∩ρSF+(T )=ϕ；

(2)intσ1(T )=intσ(T )。

证明必要性。 假设(1)不成立，则存在λ0∈ρSF+(T )，使 得 ind(T -λ0I)＞0，即 存 在λ0∈ρe(T )，使 得ind(T -λ0I)＞0。于是对任意的λ∈ρe(T ),有ind(T -λI)≥0。 显 然 intσ1(T )⊆intσ(T )，只 需 证 intσ(T )⊆intσ1(T )。 假 设λ0∈intσ(T ) 不 成 立，则 存 在μ0∈B(λ0;ε)，使 得μ0∈ρea(T ) 且 T -μ0I为 Saphar 算 子。 又 因σSF+(T )=σe(T )，则T -μ0I为Fredholm 算子。由于对任意的λ∈ρe(T ),ind(T -λI)≥0,有ind(T -μ0I)=0,μ0∈ρw(T )=ρb(T )，即μ0∈ρ(T )。于 是证 明 了 在λ0的 任 一 邻 域 内 都 存 在μ0∈ρ(T )，与λ0∈intσ(T )矛盾。故λ0∈intσ1(T )。

充分性。设(1)成立，由注解13 可证得；设(2)成立，则对任意的λ∈ρe(T ),有ind(T -λI)≥0，于是对任意多项式p，p(T )为isoloid 算子且满足Weyl定理。

对 算 子 T，σSF+(T ) =σe(T ) 在intσ1(T )=intσ(T )的判定中起重要作用。自然想到 在 定 理 5 中 ，σSF+(T )=σe(T ) 与intσ1(T )∩ρSF+(T )=ϕ 的关系。

为此，得到：

推论9设T ∈B(H )为isoloid 算子且满足Weyl 定理，则对任意多项式p，p(T )为isoloid 算子且满足Weyl 定理，σSF+(T )=σe(T )当且仅当下列条件之一成立：

(1)intσ1(T )∩ρSF+(T )=ϕ且σSF-(T )⊆σSF+(T );

(2)intσ1(T )=intσ(T )。

证明必要性。假设(2)不成立，由定理5 可知，intσ1(T )∩ρSF+(T )=ϕ。对任意的λ∉σSF+(T )=σe(T )，有λ∉σSF-(T ),即σSF-(T )⊆σSF+(T )。

充 分 性 。 当 (1) 成 立 时 ，intσ1(T )∩ρSF+(T )=ϕ，由定理5 知，对任意多项式p，p(T )为isoloid 算子且满足Weyl 定理。又由σSF-(T )⊆σSF+(T )，可得σSF+(T )=σe(T )。

当(2)成立 时，假 设 存 在λ0∈ρSF+(T ),d(T -λ0I)=∞,ind(T -λ0I)＜0, 则λ0∈intσ(T )=intσ1(T ) 与λ0∈ρ1(T ) 矛 盾，因 此，对 任 意 的λ0∈ρSF+(T )，有ind(T -λ0I)≥0，即σSF+(T )=σe(T )。由定理5 知，对任意多项式p，p(T )为isoloid算子且满足Weyl 定理。

推论10设T ∈B(H )为isoloid 算子且满足Weyl 定理，则对任意多项式p，p(T )为isoloid 算子且满足Weyl 定理，σSF+(T )=σe(T )当且仅当下列条件之一成立：

(1)intσ1(T )∩ρSF+(T )=ϕ且intσSF-(T )⊆intσ1(T )；

(2)intσ1(T )=intσ(T )。

证明必要性。假设(2)不成立，由定理5 知，存在λ0∈intσ(T )，使 得λ0∈ρ1(T )，则 存 在μ0∈B(λ0;ε)， 使 得μ0∈intσ(T ),T -μ0I为Fredholm 算子且ind(T -μ0I)＜0,因此，对任意的λ∈ρe(T )， 有 ind(T -λI)≤0, 对 任 意 的λ∉intσ1(T )， 有λ∈∂σ1(T )∪ρ1(T )， 则 存 在μ1∈B(λ;ε) 使 得 T -μ1I 为 Fredholm 算 子 且ind(T -μ1I)≤0, 因此λ∉intσSF-(T )。

充分性。当(1)成立时，intσ1(T )∩ρSF+(T )=ϕ，由定理5 可知，对任意多项式p，p(T )为isoloid 算子且 满 足Weyl 定 理。 若 存 在λ0∈ρSF+(T ) 且λ0∉ρe(T )， 则d(T -λ0I)=∞,ind(T-λ0I)＜0,λ0∈σSF-(T )，即λ0∈ intσSF-(T )⊆intσ1(T ) 与λ0∈ρ1(T) 矛 盾 。 因 此 对 任 意 的λ∈ρSF+(T ),有ind(T-λI)≥0,即σSF+(T )=σe(T )。

当(2)成立时，证明同推论9。

例13A,B ∈B(l2)，令

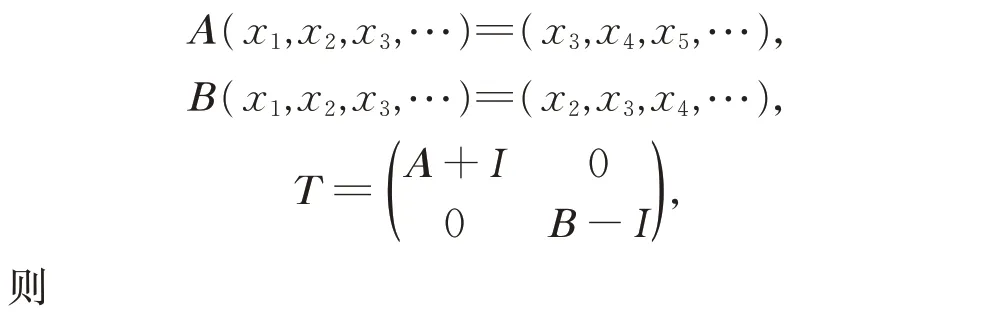
(1)σ(T )=σw(T )=σb(T )=σ1(T )={λ∈C:|λ+1|≤1}∪{λ∈C:|λ-1|≤1},π00(T )=ϕ, 说 明T 为isoloid 算子且满足Weyl 定理；

(2) 由于对任意的λ∈ρe(T ),有ind(T -λI)=3或ind(T -λI)=0，由定理4 知，对任意多项式p，p(T )为isoloid 算子且满足Weyl 定理；

(3)σSF+(T )=σSF-(T )=σe(T )={λ∈C:|λ+1|=1}∪{λ∈C:|λ-1|=1};

(4)intσ1(T )=intσ(T )，σSF-(T )⊆σSF+(T )，intσSF-(T )⊆intσ1(T ),但intσ1(T )∩ρSF+(T )≠ϕ,因此推论9 和推论10 正确。