◇ 彭 晖

数学解题，必须谨防误区，定积分问题也不例外．那么定积分问题中，有哪些误区值得我们格外注意呢?为了让学生防患于未然，笔者归纳如下，供读者参考．

1 搞错区间端点

定积分的计算体现无限分割、化整为零的思想，而分割后的每一个小区间必须表达准确．因为这是利用定义求定积分的前提，不可马虎．

例1求由抛物线y＝2x2与直线x＝0，x＝t(t＞0)，y＝0所围成的曲边梯形的面积时，将区间[0，t]等分成n个小区间，则第i－1个区间为( )．

错解因为从x＝0到x＝t得区间长度为t，平均分成n份，每个小区间长度为所以第i－1个区间为．故选C．

剖析将区间[0，1]等分成n个小区间，则第1个小区间左端点是0，第2个小区间左端点是依此类推，可知第i个小区间左端点是，因此将区间[0，t]n等分后，第i个小区间的左端点为

正解将区间[0，t]分成n个相等的小区间，每个小区间的长度为故第1个小区间为第2个小区间为第3个小区间为，故第i－1个区间的左端点为右端点为故选D．

这其实是一种容易出现的简单计算错误，唯有仔细认真方可避免此类错误．

2 错用定积分的几何意义

定积分的几何意义是求曲边梯形的面积，但它的值却有正有负，位于横轴下方部分的定积分的值为负数，作为面积的值应化负为正，这一点也同样不容忽视．

例2请用定积分表示由y＝cosx和x轴在0与2π之间围成的平面图形的面积．

错解根据曲边梯形的面积计算和定积分的几何意义，得所求面积为

剖析画图不难发现，所围成的平面图形，部分在x轴上方，部分在x轴下方，其定积分值有的为正，有的为负，但面积的值均为正，故求x轴下方的面积时，应将其积分值取绝对值．

正解所求面积的积分可分为三个部分，即[0，根据定积分的几何意义，所求面积可表示为

当x∈[a，b]时，若f(x)＜0，则由直线x＝a，x＝b，x轴和曲线f(x)围成的图形的面积应为

3 忽视积分变量

对于一个含参函数的积分，必须分清哪个变量是自变量，不可张冠李戴．避免此类错误，唯有认真审题，不可走马观花．

例3

错解

剖析对于积分变量x来说，被积函数表达式f(x)＝t2＋t为常数，它与f(x)＝x2＋x是不同的．

正解

解决定积分问题时，审题时要注意五点:一要确定好积分变量；二要清楚积分上、下限；三要明确积分的几何意义，区分积分与平面图形面积的区别与联系；四要会用导数寻找原函数；五要用好积分性质和微积分基本定理．只有这样，才可保证计算不会出错．

4 被积函数和积分上下限确定不准确

求曲边梯形的面积，必须要确定所在的位置，也就是被积函数和积分的上限与下限，不可发生半点偏离，否则难保计算准确．

例4求由抛物线y2＝8x(y＞0)与直线x＋y－6＝0及y＝0所围成平面图形的面积．

错解由，得由x＋y－6＝0，得或舍去)．故所求面积

剖析上述错解在于没有仔细分析图形，导致被积函数搞错，积分的上下限弄错．

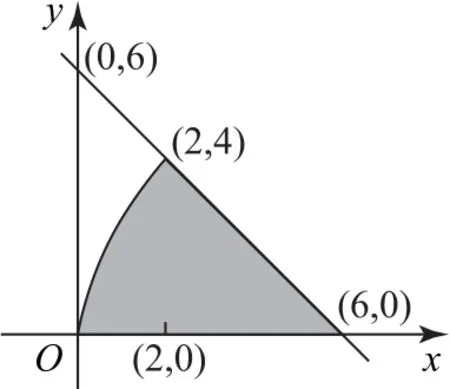
图1

正解先作出所围成平面图形的示意图，如图1所示，由得于是得到抛物线y2＝8x(y＞0)与直线x＋y－6＝0的交点(2，4)．

方法1(选y为积分变量)

方法2(选x为积分变量)

处理较复杂的平面图形的面积，一般用定积分法，但应注意以下三点:

1)要根据图形确定积分变量(选x还是y)，并确定好积分上限和下限；

2)要依据积分变量确定被积函数，当积分变量为x时，将围成平面图形的上方曲线减去下方曲线，就是被积函数；当积分变量为y时，将围成平面图形的右方曲线减去左方曲线，就是被积函数；

3)要找准原函数．