陆松建，司伟立，韩 娟,3,4，李质彬

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.中国科学院计算技术研究所 移动计算与新型终端北京市重点实验室，北京 100190；3.中国科学院计算技术研究所 无线通信技术研究中心，北京 100190；4.中国科学院大学 计算机与控制学院，北京 100049)

0 引 言

粒子群优化(particle swarm optimization，PSO)算法存在易陷入局部极值、过早收敛和收敛精度低等问题[1-4]。为解决PSO算法存在的问题，目前提出的改进方法大致分为4类：基于粒子初始化的改进，如文献[5]中利用Hammersley对粒子位置进行初始化，使初始种群能够均匀覆盖整个搜索空间；基于粒子群速度更新公式的改进，包括参数调节和公式自身改进二种方式，如动态调整惯性权重粒子群算法[6]、二阶振荡策略粒子群算法[7]，该类方法通过均衡算法全局与局部寻优能力，加强算法跳出局部最优的能力；基于分群策略的改进，如文献[8]将整个种群分为PSO机制迭代分群和混沌机制迭代分群，有利于增强种群多样性避免陷入局部极值中；基于混合机制的改进，利用其它算法优势帮助粒子群算法跳出局部最优，如模拟退火粒子群算法[9]、混沌粒子群算法[10]、免疫粒子群算法[11]等，混合算法寻优性能较好，但混合机制使得算法变得更加的复杂与繁琐。

本文基于前人的研究，提出了一种逃逸均值简化粒子群优化(escape mean simplified particle swarm optimization，EMSPSO)算法，EMSPSO算法不使用速度更新公式，在简化粒子群优化算法的基础上，加入均值搜索策略和逃逸策略，保证极快收敛速度的同时有效地改善PSO算法易陷入局部最优的问题。仿真实验中，引入5个标准测试函数，将本文算法与其它改进算法进行对比实验，验证EMSPSO算法的有效性。

1 标准粒子群优化算法

(1)

(2)

其中，x=1,2,…,n；d=1,2,…,D；t=1,2,…,M；r1和r2为区间[0,1]上均匀分布的随机数；M为种群最大进化代数；c1和c2为学习因子，分别代表个体的“自我认知”能力和群体的“社会引导”功能，c1,c2∈[0,2]；w为惯性权重，可以均衡种群的全局和局部寻优能力，w∈[0,1]； 为了预防粒子跳出解空间的搜索区间，一般设置vid∈[-vmax,vmax]，vmax为用户自行设置的常数，代表粒子的最大飞行速度；进化停止条件为预设的最大进化代数或(和)预设的目标精度阀值。

2 逃逸均值简化粒子群优化算法

2.1 简化粒子群优化算法

标准PSO算法包含速度和位置更新项，大多数改进PSO算法对速度、位置更新项增加某些操作算子，例如混沌[10]、自适应调节参数[12]、变异[13]等操作提高算法的收敛速度和精度，使得PSO算法的描述越来越复杂，同时，也使得定量分析算法的收敛性变得更加的复杂。

文献[12]尝试舍弃PSO算法中速度更新项，使算法达到最简化，仿真实验结果表明这种改进对算法稳定性影响不大，同时提高了算法的搜索效率。本文同样舍弃标准PSO算法中速度更新项，仅由位置更新项的指导进行全局寻优，得到简化粒子群优化算法(simplified particle swarm optimization，SPSO)，其公式如下

(3)

SPSO算法没有粒子速度更新概念，避免了人为设置 [-vmax,vmax] 而影响粒子的收敛速度和精度，同时，使得算法更加的简化便于对算法的进化过程进行分析。

2.2 均值搜索策略

SPSO算法无速度更新项，仅由个体粒子最优解和全体粒子最优解引导粒子进行位置更新，进化过程中，无速度因子的牵制，避免了粒子在收敛后期由于速度更新出现“发散”现象，导致粒子收敛速度慢、收敛精度低的问题。解决单峰值问题时，SPSO算法的收敛速度快、收敛精度高，但对于复杂的多峰值多局部解问题，由于无速度因子的牵制，粒子位置趋向于全局最优解更新幅度过大，导致粒子种群多样性差，全局寻优能力低，易陷于局部最优解。

(4)

式中：第一项舍弃SPSO算法中惯性权重因子w， 利用均值策略替代其它改进SPSO算法中通过调节w的方式均衡算法全局与局部寻优能力，简化了算法的操作；第二项和第三项为粒子个体最优位置和全体最优位置的线性组合。

MSPSO算法和SPSO算法进化过程如图1所示。

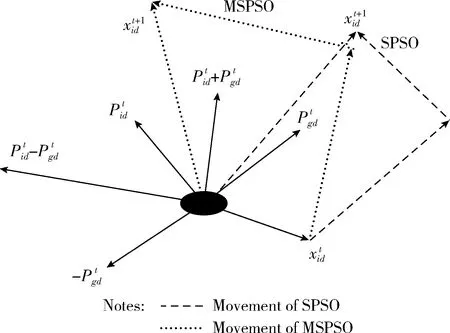
图1 MSPSO算法和SPSO算法进化过程对比

(5)

到了进化后期t→∞时，根据式(5)关系式，式(4)可变为

(6)

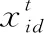
2.3 逃逸策略

粒子进化过程中，无论是早熟收敛还是全局收敛，群体中的粒子都会出现严重“聚集”现象，此时种群多样性匮乏[13]，如果粒子早熟收敛陷入局部最优解，因周围已经过高密度搜索，难以突破局部最优解。因此，当出现早熟收敛时，需提供一种机制，跳出当前局部最优解。

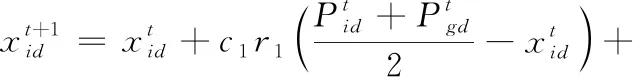
(7)

式中：r3为区间[0,1]上均匀分布的随机数；kt为逃逸控制因子，当不满足逃逸条件下，其值为0，否则代表逃逸的半径，即

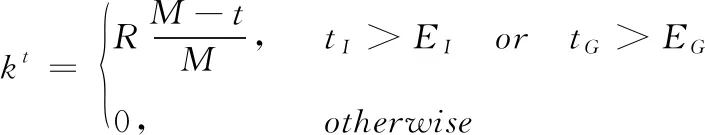
(8)

式中：t为当前进化代数；M为最大总进化代数；R为半径控制因子，控制粒子逃逸的半径，本文算法R取值为1；tI,tG分别为个体最优解停滞代数和全体最优解停滞代数；EI,EG为个体最优解最大停滞代数阀值和全体最优解最大停滞代数阀值，一般取值范围为3～8。

分析式(8)可知，当不满足逃逸条件时，公式退化为式(4)；当满足逃逸条件时，在进化前期，kt为较大值，粒子逃逸半径较大，加强全局寻优能力；在进化后期，kt为较小值，加强后期收敛能力。

2.4 算法步骤

EMSPSO算法实现步骤如下：

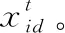
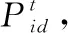
步骤3 进入进化过程，根据式(8)计算逃逸控制因子kt。

步骤4 根据式(7)更新各粒子位置，并计算各粒子位置更新后的适度值，更新个体最优解和全体最优解。

步骤5 判断个体最优解或全体最优解是否处于停滞状态，如果处于停滞状态，则分别累加各自的停滞代数tI或tG。 否则，直接执行步骤6。

步骤6 如果当前进化代数小于预设的最大进化代数或(和)当前全体最优解适度值未达到预设的目标精度阀值，则重复执行步骤3～步骤6。否则，执行步骤7。

步骤7 输出种群搜索到的最优解，进化停止，算法寻优结束。

3 仿真实验及对比分析

3.1 测试函数

为全面体现改进算法的有效性，本文从所有常用标准测试函数中挑选出5个具代表性的测试函数进行仿真对比。其中包括以Sphere为代表的单峰值函数、以Rastrigin为代表的这一类复杂多峰多局部解函数、提供极少优化信息难以极小化的Rosenbrock病态单峰二次函数、含噪声影响的Quartic函数及最优值为负数的Inverted Consine Wave函数。函数具体表达式见表1，其中D代表函数的维数。

3.2 实验设计及参数设置

本文使用Matlab R2014a进行仿真实验，仿真环境为Windows 7系统运行下在Intel(R) Core(TM) i5-75003.4 GHz的处理器中进行。在相同仿真环境与参数设置条件下，将本文改进的算法与PSO算法、改进二阶振荡粒子群优化算法(improved second-order oscillatory particle swarm optimization，ISOPSO)[7]、自适应简化粒子群优化算法(self-adjusted simplified particle swarm optimization，SASPSO)[12]进行对比实验，从收敛速度、收敛精度和稳定度3个方面验证EMSPSO算法的性能。

表1 5种标准测试函数

对比算法中各参数设置均如下：种群数量n=40； 最大总进化代数M=100； 学习因子c1=c2=2； 最小惯性权重wmin=0.4， 最大惯性权重wmax=0.9， 固定惯性权重w=0.8； 个体最优解最大停滞代数阀值EI=3， 全体最优解最大停滞代数阀值EG=5； 半径控制因子R=1。 为保证测试结果不具随机性，每个算法独立运行50次，对测试结果取平均作为更可靠的依据。

性能评估采用如下方法：

(1)总进化代数设置为100，固定进化代数情况下评估各算法解决10维问题、50维问题时收敛速度和精度。

(2)总进化代数设置为1000，固定各测试函数的目标收敛精度，评估各算法解决50维问题时达到目标收敛精度所需的平均进化代数和50次搜索中能达到目标收敛精度的搜索成功率。

3.3 收敛速度和收敛精度对比

为体现不同算法的优劣性，固定各算法总进化代数为100，从最优值、平均值、标准差、平均运行时间(s)等统计特性对算法进行评估。每个算法独立运行50次，最优值指50次搜索中搜索结果的最优值；平均值指50次搜索中搜索结果的平均值；标准差指各算法搜索结果偏离均值的程度，用于判断算法的稳定性；平均运行时间指平均运行一次算法所需要的时间。解决10维和50维的低高维度问题时，各算法搜索结果见表2。

观察50次搜索中的最优值和平均值，EMSPSO算法对函数F1的搜索结果均优于其它对比算法；SASPSO、EMSPSO 算法均搜索到函数F2和F4的理论最优解；对于极难极小化的病态函数F3，EMSPSO算法的搜索结果更加接近于函数F3的理论最优解，而其它算法均完全偏离理论最优解；EMSPSO算法对函数F5的搜索结果略差于SASPSO算法，其差距较小，收敛精度已达到很好的效果。

观察标准差，EMSPSO算法除对函数F3和F5的搜索结果略差于SASPSO算法外，对其它函数搜索结果均优于其它对比算法。而对于病态函数F3，虽然SASPSO算法标准差最小，但搜索到的最优值已完全偏离F3函数的理论最优解，因此，该算法对函数F3标准差性能的评估已失去意义。

观察平均运行时间，SASPSO算法平均运行时间最长，其算法通过添加锁定因子和自适应调节惯性权重的方式取得较好的寻优性能，但同时加大了算法运行时间，而 EMSPSO 算法取得更好性能的同时平均运行时间低于SASPSO算法，EMSPSO算法的平均运行时间更接近于其它3个算法，时间复杂度更低。

通过以上分析可知，改进算法无论解决低、高维度问题，都能保持良好的搜索性能，除对函数F5的搜索性能略差于SASPSO算法外，改进算法对其它函数的搜索，其收敛精度更高、结果波动性更小；对于含有较少寻优信息的病态函数F3，EMSPSO算法通过逃逸操作跳出局部最优解，使种群在解空间的其它区域继续搜索从而搜索到了全局最优解，搜索到的最优解更加接近于函数F3的理论最优解，而其它算法已经完全偏离理论最优解。综上分析可知，EMSPSO算法的整体寻优性能优于其它对比算法。

鉴于篇幅原因，以下选取其中3个50维函数的搜索进化曲线进一步观察算法性能，其中横坐标为进化代数，纵坐标为50次搜索结果平均适度值的对数。

各算法对Sphere函数的搜索进化曲线如图2所示，当到达最大进化代数时，EMSPSO算法更加接近于理论0值解，收敛精度最高。

表2 各算法解决10维和50维问题时搜索结果对比

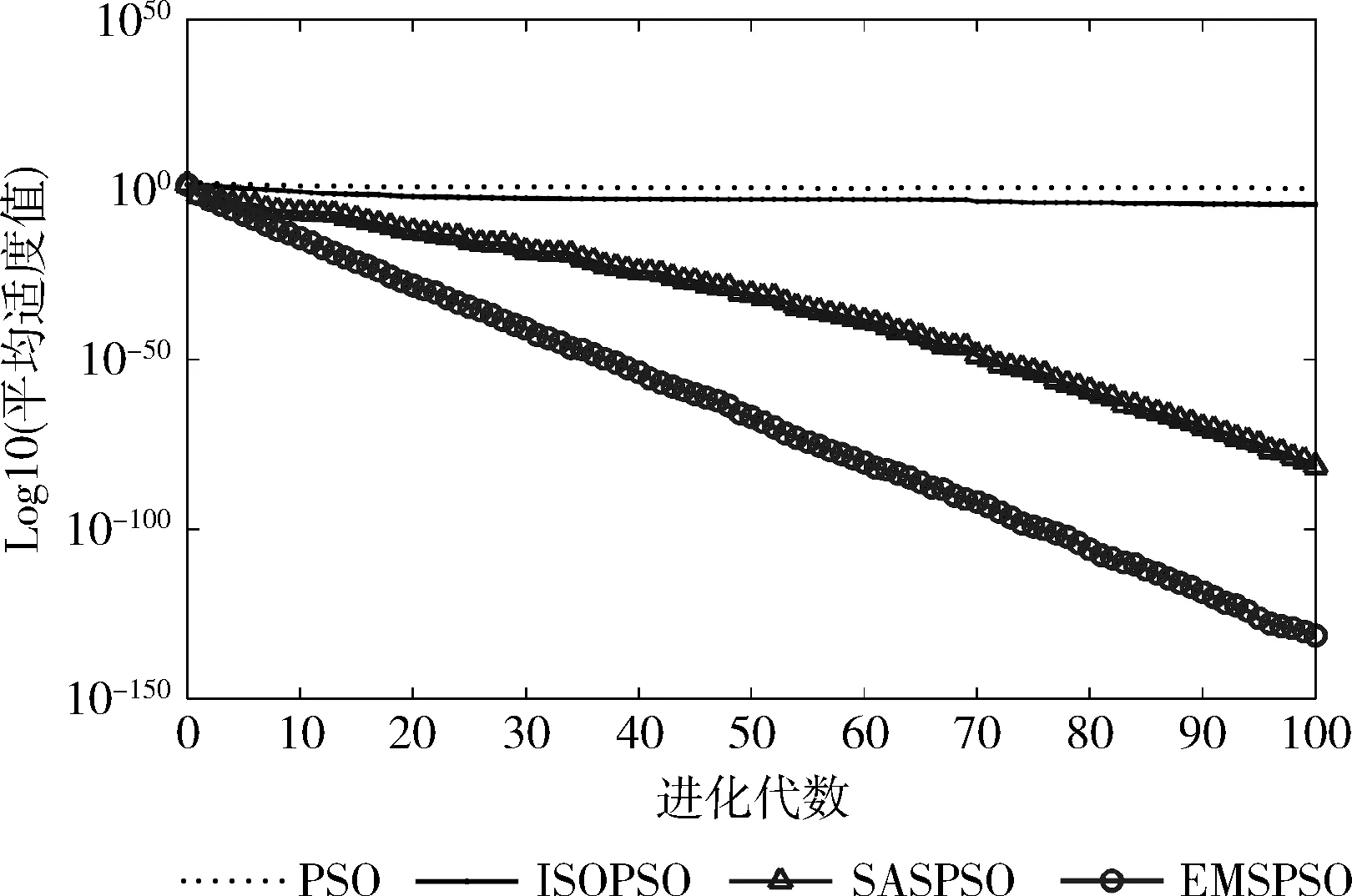
图2 50维Sphere函数搜索进化曲线对比

各算法对Rastrigin函数的搜索进化曲线如图3所示，在第12代进化左右EMSPSO算法的搜索结果已达到该函数的理论最优解，到达理论最优解所需的进化代数最少，收敛速度最快。

图3 50维Rastrigin函数搜索进化曲线对比

各算法对Rosenbrock函数的搜索进化曲线如图4所示，EMSPSO算法对Rosenbrock函数的搜索一直在逐渐逼近函数理论最优解，而其它对比算法在第15代进化左右就已陷入某个局部解中，处于搜索停滞状态。

图4 50维Rosenbrock函数搜索进化曲线对比

从图2～图4可看出，EMSPSO算法对各函数的搜索均能在20次进化代数内达到较好的收敛精度，算法收敛速度快，且进化曲线位于其它算法的下方，收敛精度更高。

3.4 平均进化代数和搜索成功率对比

表3为总进化代数为1000、重复运行50次条件下，各算法解决50维问题时达到函数目标精度所需的平均进化次数和搜索成功率对比。其中，目标精度代表解决50维函数问题所期望达到的收敛精度；平均进化次数=达到函数目标收敛精度所需进化代数总和÷达到函数目标收敛精度运行次数；搜索成功率=达到函数目标收敛精度运行次数÷总运行次数；“-”表示超过最大进化代数仍未达到函数目标收敛精度。

从表3可看出，PSO算法搜索性能最差，只有对函数F4的搜索结果能达到目标精度值，且搜索成功率较低只有34%，平均进化次数高达513.59；ISOPSO算法搜索性能相对于PSO算法更好，除函数F1外对于其它函数的搜索结果都能达到目标精度值，但搜索成功率较低；SASPSO、EMSPSO算法搜索结果均能达到函数目标收敛精度，搜索成功率高达90%以上，算法稳定性高，其中EMSPSO算法除函数F5外，达到函数目标精度所需的平均进化次数最少，搜索速度更快，性能更优。

基于以上分析结果可知，PSO算法易陷于局部最优解、收敛速度慢、收敛精度不高，其它改进算法均改善了PSO算法存在的不足，其中EMSPSO算法性能最优，主要原因在于：EMSPSO算法利用均值策略加大算法搜索范围使得算法在进化前期搜索到全局最优解的可能性更大，并且无速度因子的牵制，使得算法收敛速度更快。如果算法陷入局部最优解中，可通过逃逸策略在其它解空间继续搜索，增大算法搜索到全局最优解的几率。

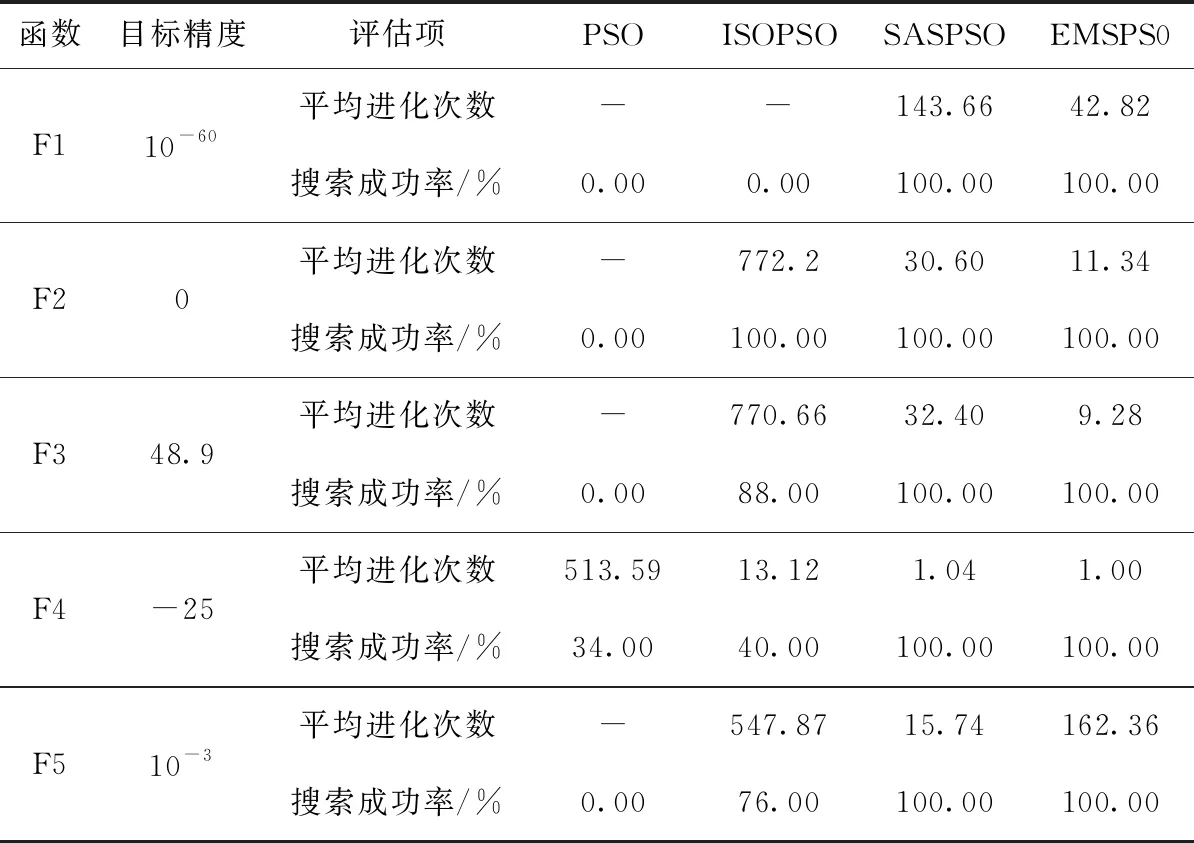
表3 解决50维问题时各算法在相同目标精度下性能评估

4 结束语

本文提出了一种逃逸均值简化粒子群优化算法，该算法在简化粒子群优化算法的基础上加入均值搜索策略和逃逸策略。均值搜索策略通过个体最优解和全体最优解的线性组合引导粒子位置更新，可扩大搜索的区域范围，提高算法的全局勘探能力。逃逸策略使进化停滞的粒子尝试从其它解空间中继续搜寻全局最优解，增大粒子种群多样性，有助于跳出局部最优解，使算法更有可能搜寻到全局最优解。最后，将改进算法应用于5个标准测试函数中，并与其它改进粒子群优化算法进行仿真对照实验，结果表明，本文改进算法全局搜索能力更强、稳定性更高，在相同目标收敛精度下所需进化次数更少，收敛速度更快。